Оценка давности наступления смерти методом нелинейного программирования в условиях изменяющейся внешней температуры

Основным физическим законом, используемым для термометрического определения давности наступления смерти (ДНС), несмотря на свой феноменологический характер, по-прежнему остаётся предложенное в 1962 г. T.K. Marshall и F.E. Hoare трансцендентное уравнение охлаждения глубоких тканей трупа:

^T - T a = ie - kt - k  e - pt

T O ^- T a    P ^- k P ^- k

где Т – температура ядра трупа, °С; Та – внешняя температура, °С; t – ДНС, ч; k – постоянная охлаждения, ч–1; р – константа температурного плато, ч–1 [1].

Одним из перспективных судебно-медицинских приложений закона охлаждения (1) является метод нелинейного программирования, позволяющий путём двукратной термометрии учесть уникальность условий охлаждения трупа и безошибочно определять ДНС при отсутствии метрологических погрешностей [2]. Данная возможность достигается путём составления на базе закона (1) системы нелинейных уравнений, отражающей результаты двукратной термометрии ядра трупа, с последующим её преобразованием в неотрицательную целевую функцию двух переменных с глобальным минимумом в точке, абсцисса которой представляет собой искомую ДНС, а ордината – индивидуальное значение константы охлаждения k [2]. Тем самым проблема определения ДНС преобразуется в многомерную задачу нелинейной оптимизации с ограничениями, решение которой сводится к нахождению точки глобального минимума полученной целевой функции.

В настоящее время вычислительный алгоритм нахождения решения сформулированной задачи нелинейной оптимизации реализован в формате онлайн-калькулятора Warm Bodies Z (свидетельство о государственной регистрации программы для ЭВМ № 2023669845), доступного по URL-адресу: [2]. Указанное приложение выполняет численное нахождение точки глобального минимума полученной целевой функции, используя гибридный итеративный алгоритм (Powell's dog leg method) из открытой математической библиотеки MINPACK [3–5]. Причём данный алгоритм оптимизации приложение выполняет для дискретного множества начальных точек, абсцисса которых всегда равна 1 ч, а ордината устанавливается перебором значений на интервале (0, 1) с шагом, равным 0,01 ч–1 [2]. Полученное множество решений затем сокращается до единственного путём исключения точек с координатами, не имеющими физического смысла.

Важным условием корректности закона охлаждения Marshall-Hoare, существенно ограничивающим применимость основанного на нём метода нелинейного программирования, является постоянство внешней температуры. В этой связи актуальность представляет разработка аппроксимаций данного метода, пригодных для использования в условиях изменяющейся внешней температуры.

Цель исследования – оценка возможностей определения ДНС методом нелинейного программирования в условиях изменяющейся внешней температуры.

Материал и методы

Методологический дизайн исследования представляет собой компьютерное моделирование охлаждения ядра трупа в условиях изменяющейся внешней температуры с последующим анализом возможностей определения ДНС при изменениях внешнего температурного режима методом нелинейного программирования. В качестве возможных аппроксимаций метода нелинейного программирования рассматривали оценки ДНС, полученные с его помощью, задавая в качестве постоянной значения внешней температуры, наблюдавшиеся в начале, середине и финале посмертного периода.

Поскольку при поиске глобального минимума целевой функции существенным образом используются установленные C. Henssge линейные взаимосвязи констант уравнения Marshall-Hoare [2], актуальные лишь для ректальной и краниоэнцефальной температур, в ходе исследования моделировали охлаждение тканей только двух указанных диагностических точек. В качестве модели изменяющейся внешней температуры рассматривали её линейные изменения, протекавшие с различными скоростями и направлениями. Динамику температуры в актуальных диагностических точках при этом вычисляли методом нелинейного программирования, используя целевую функцию, полученную аналогичным образом на основе разработанного нами ранее обобщения закона охлаждения (1) Marshall-Hoare на случай линейных изменений температуры окружающей среды [6]. Численное нахождение точки глобального минимума новой целевой функции выполняли, используя тот же гибридный итеративный алгоритм (Powell's dog leg method) из библиотеки MINPACK [3–5], реализованный в формате онлайн-калькулятора Warm Bodies Z 2 (свидетельство о государственной регистрации программы для ЭВМ № 2024614352), доступного по URL-адресу:

Оценки ДНС методом нелинейного программирования при постоянной внешней температуре находили с помощью онлайн-калькулятора Warm Bodies Z [2].

Всего было смоделировано 80 невырожденных сценариев охлаждения в условиях линейного роста

(n = 40) или падения (n = 40) внешней температуры. Из них в 24 сценариях линейного роста оценивали точность определения ДНС для ректальной, а в остальных 56 – для краниоэнцефальной температуры. Преобладание доли последних в изученных сценариях охлаждения объясняется сменой вида линейных взаимосвязей констант уравнения Marshall-Hoare для ректальной температуры трупа при внешних температурных режимах до и выше 23,2 ºС [7, 8], вследствие чего вычисление ректального температурного профиля в указанных условиях становилось невозможным.

Абсолютная скорость изменений внешней температуры в изученных сценариях охлаждения варьировала от 0,1 до 4,0 К/ч, внешняя температура на момент первой термометрии трупа – от –10 до 23 ºС, температура трупа при первом измерении – от 5 до 36 ºС, посмертный период изменялся в пределах от 3,97 до 45,36 ч, а интервал времени между первой и повторной термометриями трупа – от 1 до 3 ч. Начальную температуру тела в момент наступления смерти для обеих диагностических точек во всех сценариях охлаждения задавали равной 37,2 ºС. Величину ошибок определения ДНС находили путём вычитания из истинных значений ДНС их аппроксимационных оценок.

Полученные данные компьютерного моделирования подвергали математико-статистической обработке, включавшей дескриптивное оценивание и корреляционно-регрессионный анализ. Силу связи между исследуемыми показателями выражали с помощью коэффициента корреляции Пирсона, статистическую значимость которого определяли с использованием двустороннего варианта t-критерия. Построение регрессионных моделей осуществляли методом наименьших квадратов. Статистическую значимость регрессионных уравнений проверяли с помощью F-теста. Во всех использованных статистических методах результаты признавали значимыми при величине ошибки первого рода α < 0,05.

Математико-статистическую обработку данных выполняли с использованием табличного процессора Excel из пакета Microsoft Office 2016.

Результаты

При использовании нелинейного программирования для определения ДНС в условиях изменяющейся внешней температуры оказалось, что наилучшими аппроксимациями независимо от вида термометрии трупа являются оценки, полученные на основе финальной внешней температуры, зарегистрированной в ходе осмотра трупа. При этом во всех сценариях охлаждения имела место систематическая ошибка аппроксимационных оценок, знак которой зависел от типа внешнего температурного тренда в посмертном периоде:

t = t + 8 , где t – аппроксимационная оценка ДНС, а ε – её ошибка, ч. В частности, отрицательными ошибки всегда были при росте внешней температуры, а положительными – при её снижении.

Пример 1

Охлаждение трупа происходило в условиях линейного роста внешней температуры, протекавшего со скоростью 0,5 К/ч, со следующими индивидуальными значениями констант охлаждения и температурного плато: k = 0,065415 ч–1, р = 0,327074 ч–1. Ректальная температура при первой термометрии трупа равнялась 25,0 °C, при повторной, выполненной спустя 1 ч, – 24,1 °C. Длительность посмертного периода на момент первой термометрии тела составила 11,5 ч. Внешняя температура в начале, середине и финале посмертного периода равнялась 4,25; 7,13 и 10,00 °C соответственно.

Аппроксимационные оценки ДНС, вычисленные методом нелинейного программирования с помощью онлайн-калькулятора Warm Bodies Z, приняв в качестве постоянной внешней температуры её начальное, среднее и финальное значения, составили 14,39; 13,63 и 12,73 °C соответственно (рис. 1).

Таким образом, в условиях роста внешней температуры наиболее точной оценкой ДНС являлось её приближение, полученное на основе финального значения внешнего температурного тренда с отрицательным смещением, по модулю равным 1,236 ч.

Пример 2

Охлаждение трупа происходило в условиях линейного падения внешней температуры, протекавшего со скоростью 0,5 К/ч, со следующими индивидуальными значениями констант охлаждения и температурного плато: k = 0,074983 ч–1, р = 0,631734 ч–1. Краниоэнцефальная температура при первой термометрии трупа равнялась 25,0 °C, при повторной, выполненной спустя 1 ч, – 23,9 °C. Длительность посмертного периода на момент первой термометрии тела составила 10,52 ч. Внешняя температура в начале, середине и финале посмертного периода равнялась 15,26; 12,63 и 10,00 °C соответственно.

Аппроксимационные оценки ДНС, вычисленные с помощью онлайн-калькулятора Warm Bodies Z на основе начального, среднего и финального значений внешней температуры, составили 7,83; 8,71 и 9,44 °C соответственно (рис. 2).

Таким образом, в условиях снижения внешней температуры наиболее точной оценкой ДНС являлось её приближение, полученное на основе финального значения внешнего температурного тренда со смещением, равным 1,084 ч.

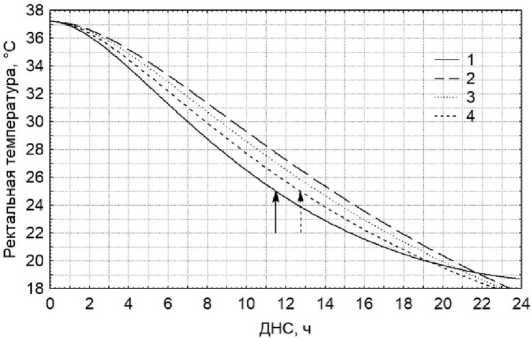
Рисунок 1. Графики ректальной температуры и её аппроксимационных оценок, полученных методом нелинейного программирования, при линейном росте внешней температуры для данных из примера 1. Условные обозначения: 1 – истинная динамика ректальной температуры; 2 – температурный профиль, вычисленный приняв начальную внешнюю температуру в качестве постоянной; 3 – температурный профиль, вычисленный приняв в качестве постоянной среднюю за посмертный период внешнюю температуру; 4 – температурный профиль, вычисленный приняв финальную внешнюю температуру в качестве постоянной. Сплошной стрелкой обозначен истинный посмертный интервал, штриховой – его наиболее точная аппроксимационная оценка

Figure 1. Graphs of rectal temperature and its approximate estimates obtained by nonlinear programming with a linear increase in ambient temperature for the data from Example 1. Symbols: 1 – true dynamics of rectal temperature; 2 – temperature profile calculated by assuming the initial ambient temperature as a constant; 3 – temperature profile calculated by assuming as a constant, the average ambient temperature for the postmortem period; 4 temperature profile, calculated by taking the final ambient temperature as a constant. A solid arrow indicates the true postmortem interval, a dashed arrow indicates its most accurate approximate estimate

Неизменный граничный характер и независи- мость типа аппроксимационных оценок от вида динамики внешней температуры позволяют использовать нелинейное программирование и реализующий его онлайн-калькулятор Warm Bodies Z для вычисления предельных значений ДНС в условиях изменяющегося внешнего температурного режима. Причём тип пределов (верхний или нижний) определяется разностью среднего и финального значений внешней температуры в посмертном периоде. Так, если средняя внешняя температура выше финальной, то полученная методом нелинейного программирования оценка является нижним пределом ДНС. Если же средняя за посмертный период внешняя температура ниже финальной, то аппроксимационная оценка служит верхним пределом ДНС.

Величина ошибок определения ДНС методом нелинейного программирования коррелировала как в сценариях линейного роста (r = –0,858; t = –10,303; p = 1,479·10–12), так и падения (r = 0,892; t = 12,184; p = 1,073·10–14) внешней температуры с интегральным показателем, представлявшим собой произве- дение длины посмертного интервала на модуль разности среднего значения внешней температуры за этот период и её значения в конце последнего: a    Ta -Ta a aa

,

где ^{T a} – среднее значение внешней температуры за весь посмертный период, ч (рис. 3).

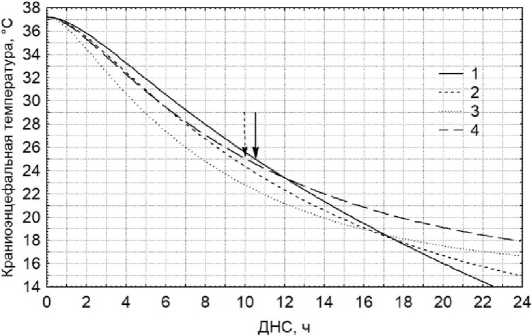
Рисунок 2. Графики краниоэнцефальной температуры и ее аппроксимационных оценок, полученных методом нелинейного программирования, при линейном росте внешней температуры для данных из примера 2. Цифрой 1 обозначена истинная динамика краниоэнцефальной температуры. Остальные обозначения те же, что и на рисунке 1

Figure 2. Graphs of cranioencephalic temperature and its approximate estimates obtained by nonlinear programming with a linear increase in ambient temperature for the data from Example 2. The number 1 indicates the true dynamics of cranioencephalic temperature. The other symbols are the same as in Figure 1

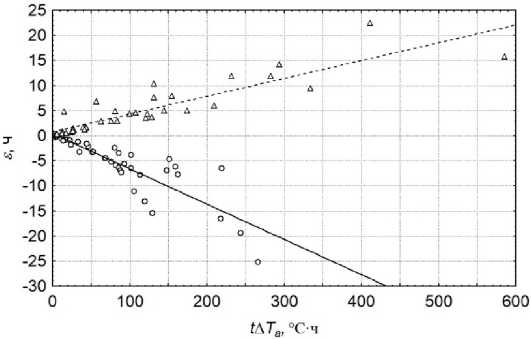
Рисунок 3. Диаграммы рассеяния ошибок аппроксимационных оценок ДНС в зависимости от величины t ∆ Ta. Условные обозначения: ○ – ошибки при росте внешней температуры; Δ – ошибки при снижении внешней температуры. Приведены линейные регрессии, полученные методом наименьших квадратов

Figure 3. Error scattering diagrams of the approximation estimates of the postmortem interval depending on the value of t ∆ Ta. Symbols: ○ – errors with a increase in ambient temperature; Δ – errors with a decrease in ambient temperature. Linear regressions obtained by the least squares method are presented

Данное обстоятельство делает возможным установление величины отклонений результатов определения ДНС методом нелинейного программирования по интегральному показателю (2), используя в нём вместо неизвестных значений ДНС и средней внешней температуры их точечные оценки.

В частности, среднюю величину систематических отклонений оценок ДНС, полученных методом нелинейного программирования, можно вычислить с помощью регрессий:

e = - 0,019920 t| T _a - T _a| e = - 0,084077t|T _a - T _a|

с остаточными стандартными отклонениями, равными 2,7 и 3,6 ч соответственно.

Регрессия (3) отличалась высокими значениями коэффициентов корреляции (r = 0,941) и детерминации (r 2 = 0,885), а также F-теста (F = 301,306; р = 1,170·10^–19). Аналогичные показатели регрессии (4) были несколько ниже, но также отражали высокую силу анализируемой корреляционной связи (r = 0,853; r 2 = 0,728, F = 301,306; р = 1,829·10^–12).

Визуальный анализ диаграмм рассеяния показал (см. рис. 3), что дисперсия ошибок аппроксимационных оценок ДНС увеличивается с ростом интегрального показателя (2). Для уменьшения дисперсии ошибок целесообразно ограничить области определения уравнений (3) и (4). В частности, применение регрессии (3) показано при значениях интегрального показателя (2) не более 150 °С·ч, а регрессии (4) – при значениях интегрального показателя (2) не более 75 °С·ч и модуля разности средней и финальной внешних температур не более 3 °С.

Среднее значение внешней температуры, входящее в качестве одной из переменных в уравнения (3) и (4), в общем случае вычисляется как

T

T a = -f Т а Wdt

0 , (5)

где Т а (t) – функция внешней температуры от времени, прошедшего с момента наступления смерти, а τ – ДНС, обозначенная таким образом для исключения путаницы с переменной интегрирования.

Пример 3

В изученных сценариях охлаждения скорость изменения внешней температуры в посмертном периоде была постоянной:

T a ( t ) = v

^, откуда

Ta (t )= Ta0 + Vt , где Та0 – начальная внешняя температура, °C; v – почасовая скорость изменения внешней температуры, К/ч. Тогда в соответствии с уравнением (5)

T_a = ^- f(T_a + vt)dt = T_a0 + —. a т J ' ao ' a0 2 ^.

При нелинейных изменениях внешней температуры целесообразно сначала аппроксимировать их какими-либо функциями, например полиномами 2–4 степеней, а затем находить их средние значения по формуле (5). Найти адекватную аппроксимацию можно с помощью любого доступного табличного процессора, например Excel.

Обсуждение

Нелинейное программирование представляет собой наиболее перспективный и точный способ термометрического определения ДНС среди методов, основанных на феноменологической теории охлаждения трупа, а также машинном обучении [9, 10], поскольку обеспечивает математическую конкретизацию процесса охлаждения в данных уникальных условиях. В настоящее время разработаны и являются доступными онлайн-реализации метода, позволяющие вычислять ДНС в условиях постоянной или линейно изменяющейся внешней температуры. Однако более сложные изменения температурного тренда нелинейного характера, преимущественно наблюдающиеся при нахождении трупа вне помещений со стационарной температурой воздуха, существенно ограничивают использование алгоритмов нелинейного программирования в судебно-медицинской экспертной практике [11, 12].

В рамках проведённого исследования показано, что нелинейное программирование может с успехом применяться для определения ДНС в условиях изменяющейся внешней температуры. Для этого в вычислительном алгоритме метода в качестве постоянной следует учитывать внешнюю температуру, зарегистрированную при первичной термометрии трупа на месте его обнаружения. Полученная таким образом оценка, в зависимости от возрастающего или убывающего характера внешней температуры, представляет собой соответственно максимальное или минимальное предельное значение ДНС. При этом смещение аппроксимационной оценки от истинной продолжительности посмертного интервала может быть вычислено по регрессиям (3) или (4) с последующим нахождением непосредственно ДНС.

Каких-либо других способов определения ДНС в условиях изменяющейся температуры, основанных на феноменологической теории охлаждения трупа, не существует.

Реализация изложенного метода нелинейного программирования предполагает выполнение двукратной ректальной или краниоэнцефальной термометрии трупа в ходе его осмотра на месте обнаружения. Противопоказаниями к использованию метода являются изменения условий охлаждения трупа и техники его динамической термометрии, а также значительная (более 0,01 °C) инструментальная погрешность средства измерения температуры трупа. Влияние последней на результат определения ДНС при необходимости можно визуально и количественно оценить с помощью онлайн-калькулятора Warm Bodies Z, воспроизводящего вычислительный алгоритм метода [2].

Заключение

Нелинейное программирование делает возможным определение ДНС в условиях изменяющейся температуры внешней среды путём учёта в вычислительном алгоритме метода в качестве постоянной внешней температуры её значения, зарегистрированного при первичной термометрии трупа на месте его обнаружения. Полученные аппроксимационные оценки, в зависимости от возрастающего или убывающего характера внешней температуры, представляют собой соответственно максимальное или минимальное предельное значение ДНС. Величина смещения аппроксимационной оценки и собственно ДНС могут быть вычислены с помощью разработанных регрессионных уравнений, для реализации которых требуется предварительное установление средней внешней температуры за оцененный методом нелинейного программирования посмертный период. Предложенная адаптация метода нелинейного программирования рекомендуется для экспертного установления ДНС в условиях изменяющейся внешней температуры.