Оценка дифракционного размытия фокальной линии геометрооптических фокусаторов

6 данной работе решается задача дифракционного расчета интенсивности поля вблизи фокальной линии фокусатора когерентного излучения. Метод основан на вычислении интеграла Кирхгофа в параксиальном приближении в системе координат, связанной со слоями на фокусаторе, уравнения которых находятся в процессе реше ния обратной задачи. Приведены примеры расчетов световых полей в случае фокуси ровки плоского гауссова пучка в отрезок с равномерным распределением интенсивности. Получены простые выражения для дифракционной ширины фокального отрезка и энергетической эффективности фокусатора.

Пусть рассматривается задача фокусировки плоского пучка когерентного излучения с длиной волны X в плоскую фокальную линию F с параметрическими уравнени ям и х=х0(Е), Ее[о, ь],                                                             (1)

где 1(E)* линейная плотность; Х=(х, у) - декартовы координаты в плоскости фокусировки; Е - натуральный параметр кривой.

Фокальная плоскость отстоит на расстояние f от плоскости фокусатора (это расстояние будем называть фокусным) .

Определим координаты в окрестности фокальной линии. Для этого введем линейное продолжение F линии F касательными в концевых точках согласно уравнениям:

х=х0(Е)+х;е(Е-Ё), ё -

где

Е» если Е€[0, L] ;

О, если Е<0;

L, если E>L,

При g£[0, L] величина I g-g I есть расстояние от точки х до соответствующей граничной точки прямой, измеренное по касательной.

Далее введем в плоскости фокусировки криволинейные координаты g, п, связанные с х, у соотношениями:

У=Уо^>+хоЕ' п;                                                        (3)

х=х0(Е)-у;£п.

Координата п» выбранная таким образом, характеризует отклонение точки х от кривой F, отсчитанное по нормали.

В геометрооптическом решении обратной задачи фокусировки [l-З] каждая точка g фокальной линии формируется соответствующим слоем, имеющим в параксиальном приближении уравнение (u-x0(g))x'(g)=c(g)f0,                                                    (4)

где функция c(g) находится из энергетических соотношений.

Результатом решения обратной задачи фокусировки является фазовая функция фокусатора кФ [2], определяемая уравнением 1 u              (u-x^2 U-Uo)xc

Ф(и) = т- / Xo(g(u))dl----—г----- , го u0                            го где . 2п к = у— - волновое число; u=(u, v) - декартовы координаты в плоскости фокусатора.

В дифракционном решении прямой задачи фокусировки будем считать, что поле в каждой точке в окрестности фокальной линии формируется лишь той частью излучения, которая проходит вблизи соответствующего слоя фокусатора. Отдельно для каждой точки Е линии F построим систему декартовых координат в плоскости фокуса тора так, чтобы ось В совпадала с соответствующим слоем U=(c(g)fo+xo(g)x'oS(g))x;(g)+x;g(g)xB); v=(c(g)f0+x0(g)x;E(g))y'(g)+(x;E(g)-в),                                (5)

где ххв=ха-у0, (х-В)=хВ+уа.

Расчет поля w(x, f0) в фокальной плоскости проводим с помощью интеграла Кирхгофа в параксиальном приближении [^]

w(x, f₀)=e^ikf° 2_nif~ Vw₀(u, 0)exp(1кФ)d³u,                                (6)

где

Ф = ^j-(x-u)2+T.                                                           (7)

Анализируя фазу Ф, можно убедиться, что множество точек стационарной фазы образует прямую линию, совпадающую со слоем на фокусаторе.

Сделаем в (6) замену переменных (u, v)—(a, В) и разложим Ф(а, В) в ряд Тей лора, ограничившись квадратичными членами, а функцию wQ аппроксимируем ее зна чением на соответствующем слое (то есть при а=0) . Далее вычисляется интеграл по В; получаем

w(x, f0)=e1K -^— /dB(w0 (и (0, В), 0)ехр(^(хо 2пг                             1 о

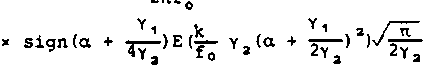
G (В)

G_(B)’

^П *

где

• Y₀⁼^о^*а=о' ^Yi ~ Эа^°1а=0,

4-^l  , E(x> . Л/е^ах,

• ^{1   2} la'Ia-O           ⁿ

x - фаза, не зависящая от a и g, a=G1(В) и a=G3(B) уравнения границ фокусатора, которые находятся из уравнений границ в переменных (u, v) с использованием соотношений (4) и (5).

Если в (8) 0,(0)=», Ga(B)=-“, получим асимптотическую Формулу

w(x, f₀) = ^V^ ^_д| w(u(0, 0) ,O)exp(^|p)

В частности, формула (9) справедлива всюду, если фокальная кривая замкнута и гладкая, а также справедлива для окрестности внутренних точек, достаточно удаленных от концов произвольной фокальной кривой. Интенсивность поля рассчитывается по формулам (8) и (9) путем вычисления квадрата модуля.

В качестве примера рассмотрим фокусировку в фокальный отрезок прямой с равномерной линейной плотностью (рисунок). Отрезок предполагается расположенным вдоль оси и симметрично относительно начала координат, а фокусатор - прямоугольным размера 2а х 2Ь. Для него Е=х, п=У, а слои представляют прямые, параллельные оси V.

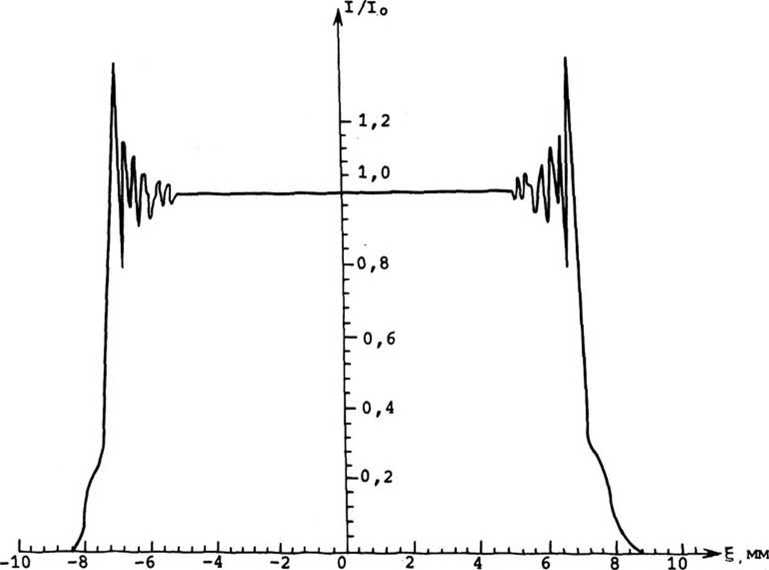
Распределение интенсивности от фокусатора гауссова пучка в отрезок (А—10,6 мк, а-10 мм, а-12,5 мм, L-15 мм)

Для фокусируемого пучка, имеющего плоский волновой фронт с равномерным рас пределением интенсивности

Ф(и, v) = - «1(1 L ) -      ,

2to 23    2t0

а поле в фокальной области определяется согласно (8), выражения w (Ей) = f Ь sine (^т^) х [sign (а - хЕ ((7—) ) + nLfo        nf0        3        L До

+ sign (а + ^)xE(ka_(g + |) з} .

/И"о                         I 1 X>0

До = v т—— ; Д = g - •= sign x = < 0 x=0

• -1 x<0 .

Соотношение (10) позволяет представить данный фокусатор как две скрещенные линзы с фокусами f0/(l - ^-) и fQ по осям и и v соответственно. Заметим, что по ле (11), рассчитанное по формуле (8) вдоль оси g, описывается формулами дифракции Френеля сферического сходящегося пучка на щели шириной 2а, а вдоль оси п -формулами дифракции Фраунгофера на щели шириной 2Ь.

При L—0 мы получаем поле от линзы с апертурой 2а х 2Ь и фокусным расстоянием fQ.

При —д = |Д|>>Д0, то есть для внутренних точек, лежащих вдали от концов отрезка, формула (11) асимптотически переходит в

w(gn) = wosinc(^p),                                                    (12)

/я v т> описывает усредненное от оси значение комплексной ампли- туды, а sine-функция описывает дифракционное уширение До фокальной кривой.

При Д0«Ь для уровня 6 по интенсивности получим

2nf°         Г

До = -k^ arsine ve, где символом arsine обозначена функция обратная к sine (х). Формула (12) позволяет оценить дифракционную эффективность фокусатора ед, то есть долю энергии, попадающую в прямоугольник с шириной Дд и длиной L eg = ~(SI (2пх) -nO^I x=arsincV§.

Для фокусируемого гауссова пучка с плоским волновым фронтом и распределением интенсивности

1=1 ехр(- —^—),

2а3

согласно (8) и (9), выражение для амплитуды имеет вид:

е      2rrf          L w(gn) = ' eix Zta \/2nerf (^y)k

) - w2 при Д»Д0; (13) x (signAE ( (y-) 3) - ^Mwn при А°Дог

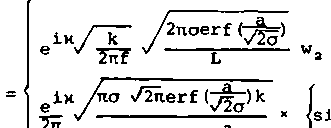
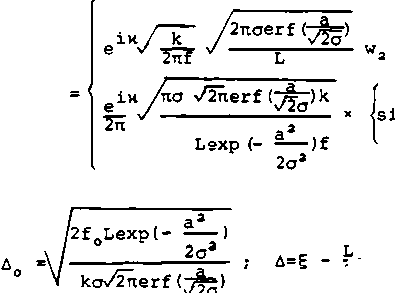
Lsxp (-где I2f Lexp(- ---) ,    \ /               2aa . A_                        a     r V koVSnerf (^5) wn = / exp(i£nv) exp(- -

— )f 1 2a3 Д=Е - j; —)dv.

В случае, когда размеры фокусатора больше, чем характерный размер пучка о

Wy принимает вид 2 wn=2o\HT ехр(- ——) , 452

где 3 = ^ , совпадающий с известной формулой для фокусировки гауссова пучка линзой.

При этом 2 f            1 /

Де = kS?(- ine) =;

eg = erf (v^Tn©) .