Оценка движения в видеопоследовательности на основе тензорного подхода

Информация о движении в видеопоследовательности может быть использована в разных областях: сжатия видео, в системах видеонаблюдения, при реализации интерфейса между человеком и компьютером, в системах анализа дорожного трафика и т. д. В данной статье будет рассматриваться метод оценки движения, основанный на тензорном подходе.

Анализ последовательных кадров приводит к пространственно-временному набору изображений с двумя пространственными и одним временным измерением. При движении в видеопоследовательности структуры с определенной ориентацией в наборе кадров происходит ее трансформация. Например, точка в линию, направление которой напрямую связано с ее смещением. Мощным инструментом представления локальной ориентации является ориентированный тензор.

Тензорный подход относится к методам, основанным на уравнении оптического потока - стандартном уравнении в частных производных, используемом в физике для описания процессов переноса различных сред:

d _tF + v -V F = S , (1) где d t F - производная по времени; V F - пространственный градиент функции. В уравнении (1) под переносимой средой понимается яркость изображения F , а член S в правой части моделирует источник, определяющий изменения яркости, не сводимые лишь к пространственному движению.

Задача состоит в определении поля векторов движения (1) на основе знания о сигнале яркости в двух соседних кадрах. Например, за вектор движения можно принять вектор, минимизирующий правую часть уравнения (1) по всей площади макроблока. Если представить вычисления в матричном виде, то для вычисления векторов движения можно использовать тензорную алгебру.

При тензорном подходе последовательность кадров представляется в виде единой трехмерной структуре [1-3]. Смещение значения интенсивности этой структуры внутри последовательности изображений дает структуру, которая направлена вдоль временной оси пространственно-временного объемного изображения.

Запишем уравнение оптического потока в векторной форме [4]:

V g ^T v = 0, (2) где V g - пространственно-временной градиент функции интенсивности; v = (A x 1 , A x ₂, A t ) ^T - смещение интенсивности во времени, от кадра к кадру. Из выражения (2) следует, что градиент V g ортогонален вектору смещения v .

Введем функцию стоимости, определенную для окрестности w ( x - x ‘) с центром в точке х , для которой ищется вектор смещения и в которой он постоянен:

X -12

• e( v ) = J w ( x - x ' ) [v g ^T v ] dx ' . (3) -X

Для решения задачи поиска оптического потока необходимо найти такой вектор v , который минимизирует функцию стоимости e( v ), и наложить ограничение || v || = 1 для исключения нулевых значений вектора v .

Сделаем следующую замену:

X

(a^ = J w(x - x')adx'. (4) -X и получим

e( v ) = ([V g ^T v ] 2\ = (v ^T V g V g ^T v;.        (5)

Из предположения, что скорость v постоянна в окрестности w ( x - x ‘), следует, что значение v можно вынести из-под знака интеграла:

e = v ^T ^V g V g T ^v = v T Jv ,            (6)

где J - произведение пространственно-временного градиента самого на себя, представляющее симметричный трехмерный структурный тензор:

gxgx	gxgy	( gxg?)
gxgy	gygy	g gyg?)
gxgt	gygt	к gtg?) _

Элементы J определяются как

X

^Jpq = ( g p g q ) = J w ⁽ x - x ' ) g p g q dx ' ,         ⁽⁸⁾

-X где gp, p e {x, y, t}, определяет частную производную по координате p.

Исходя из ограничения || v || = 1, воспользуемся методом Лагранжа и минимизируем составленную функцию L ( v ,X):

L ( v , X) = v ^T Jv + X(1 - v ^T v ).          (9)

Параметр Лагранжа X выбирается таким образом, чтобы все производные L ( v , X) по всем трем координатам v были равны нулю:

S L ^vi^) = 2 ^ J ^ v_k - 2X v = 0, i e {1, 2, 3}. (10) ^{d v} i k

Представим уравнение в виде линейной системы уравнений

Jv = X v .                      (11)

Таким образом, задача минимизации сводится к задаче поиска собственных значений симметричной матрицы J. После минимизации формула (6) принимает вид e = vT Jv = vT Xv = X, (12)

который показывает, что минимум e определяется собственным вектором матрицы тензора J , соответствующим минимальному собственному значению X.

Вначале необходимо построить тензор по формуле (7), элементы которого вычисляются по формуле (8). Для практического применения интеграл заменяют на взвешенную или простую сумму, например для окрестности (2 w x + 1) х (2 w y + 1) точки х = ( x , y , t ) ^T :

i = x + w x j = y + w y

• ^Jpq = E E ® ij g p g q . ⁽¹³⁾

i = x - w x j = y - w y

Здесь g_p , p e { x, y , t }, задает частную производную по координате p , m j - вес соответствующей точки. Пространственные производные по x и y для точки х определяются соответствующими операторами Собела,

Шарра или другими. Временная производная является разностью между текущим и следующим значениями интенсивности в точке x :

g t = I t ⁽ x , y ) - It -1 ⁽ x , y )• ⁽¹⁴⁾

Структурный тензор содержит внутреннюю информацию о распределении яркости в пределах локальной пространственно-временной окрестности. В трехмерной пространственно-временной структуре путем анализа ранга структурного тензора, который получается из числа ненулевых собственных значений, могут быть выделены и определены четыре различных класса [5].

Первый класс – это класс постоянной яркости. В этом случае ранг ( J ) = 0 и все собственные значения вектора смещения, т. е. все частные производные вдоль главных осей, равны нулю:

λ 1 = λ 2 = λ 3 = 0.

Таким образом, распределение яркости остается постоянным в U , и нет движения, которое мы можем оценить. Этот класс можно отличить по сумме всех собственных значений, которая равна следу J 0 :

trace( J ' ) = trace( J ) = £ J pp ,

i где trace (J) – след структурного тензора, который можно обнаружить, сравнивая его с порогом:

trace( J ) <  t , (15)

перед нахождением собственных значений. Для этих точек поиск собственных значений может быть полностью пропущен, а порог t выбирается исходя из уровня шума видеопоследовательности.

Второй класс возникает, если ранг ( J ) = 1 и структуры изображения имеют пространственную ориентацию и движутся с постоянной скоростью.

Если пространственно-временная структура проста, т. е. направлена вдоль одной линии и только одно из собственных значений больше нуля:

λ1> 0, λ2= λ3= 0, то возникает проблема апертуры, которая заключается в следующем. Если движущаяся линейная структура наблюдается через небольшое отверстие, то единственное смещение, которое может быть определено, является компонентой, перпендикулярной к структуре (рис. 1). Окрестности, помеченные как P, содержат изображения простых локальных структур и для них можно оценить только нормаль смещения. Окрестности же, обозначенные как L, не являются простыми и для них можно определить истинное смещение.

Теперь вычислим нормаль движения к линейной структуре. Для этого рассмотрим локальную линейную структуру, движущуюся с компонентой смещения

v v = 1 1 I, (16) Iv 2 J по двумерному изображению. Если смещение происходит в единицу времени на каждый кадр в последовательности, то это означает, что любая точка линейной структуры перемещается на расстояние между каждым кадром, равное в 3D v1

v = v 2

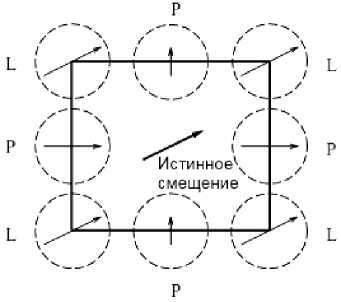
Рис. 1. Проблема апертуры при оценке движения

Вектор v называют пространственно-временным вектором смещения. Этот вектор находится в постоянной трехмерной плоскости, которая появилась при движении линейной структуры, т. е. v является собст- венным вектором ориентированного тензора и его собственное значение равно 0. Поскольку сигнал в этом случае является локально простым, то соответствующий ориентированный тензор имеет ранг 1.

Если λ 1 является наибольшим собственным значением соответствующего нормализованного собственного вектора