Оценка фазочастотных характеристик выходных цепей устройств е-класса

Публикации прошлых лет [1; 2], а также литературные источники последних лет [3–8] свидетельствуют о наличии постоянного интереса к усилителям и автогенераторам, работающим в режимах Е-класса на частотах с заходом в СВЧ-диапазон. Для таких усилителей и автогенераторов предложены модели, рассчитаны величины элементов их входных и выходных цепей, при которых электронный КПД устройств стремится к максимально возможной величине. Вместе с тем оценка фазочастотных характеристик выходных цепей устройств Е-класса в литературе отсутствует. Цель данной статьи – выполнить такую оценку и на ее основе дать рекомендации по коррекции известных методик проектирования выходных цепей устройств Е-класса.

Ход исследования

Рассмотрим на рис. 1 типовую модель устройства Е-класса. Транзисторный элемент с источником питания представим в виде ключа с внутренним активным сопротивлением r _к, величина которого меняется скачком от нуля до бесконечности. Характерной для реальных СВЧ-транзисторов емкостью ключа в данной модели пренебрежем. Выходная цепь является реактивной и обычно содержит соединенные последовательно формирующий qf ₁ и фильтрующий f ₁ контуры. С ее помощью на выходе ключевого активного элемента

формируются необходимые для работы класса Е импедансы нагрузок Z_k ( f_k ) на основной частоте f ₁ и ее гармониках f_k . Формирующий контур, который в q -раз расстроен относительно частоты возбуждения, в этом процессе играет главную роль. Благодаря этому контуру в моменты включения (выключения) транзисторного ключа реализуются условия равенства нулю либо тока, протекающего через ключ, и его производной, либо напряжения на ключе и его производной. Другими словами, реализуется режим «переключения при нулевом напряжении или при нулевом токе» [1]. В результате устраняются коммутационные потери в моменты либо включения транзистора, либо его выключения соответственно. Нагрузкой выходной цепи является специально рассчитанное для работы в классе Е сопротивление R _E, которое принципиально отличается от сопротивлений стандартных трактов. Типовое устройство Е-класса может также содержать (а может и не содержать) цепь согласования этого сопротивления R _E со стандартной 50-омной нагрузкой.

Если обратимый (взаимный) реактивный четырехполюсник, каким является выходная цепь на рис. 1, описать унитарной [S]-матрицей, то для него при S 12 = S 21 и Ф 12 = Ф 21 выполняется выражение [9]:

Фи + ф ₂₂ = 2 ф 12 ±п ,                               (1)

где фи , Ф 22 , Ф 12 , Ф 21 — аргументы соответствующих элементов [S]-матрицы.

2кта k= 1,2...со	1 1	9fl		/1		Re^ 50 Ом| 1                 .
КЛЮЧ N	1	Форм.		Фильтр.			Нагрузка	1 1 I J	| Согла- 1 1 сующая I цепь 1 1                J
питания	1	контур		контур			Re	1      1
	1 L		Выходная цепь					1 1

J Нагрузка I 50 Ом

Рис. 1. Типовая модель устройства Е-класса

Fig. 1. Typical model of an E class device

В терминах [S]-матрицы входной коэффициент отражения Г _вх четырехполюсника определяется через коэффициент отражения Г _н от его нагрузки R _E так:

S 12 S 21 ^Г н

1 вх = S11 + d c

¹ S 22 ¹ н

.

Тот же входной коэффициент отражения Г _вх можно определить через входной импеданс четырехполюсника Z _вх( f_k ) и сопротивление r _к по-другому [10]:

Г = ^Zbx ⁽ fk ) ^г к                                         (з)

^ВХ Z _Bх( f ) + r_K ‘ вх к

В режиме полного согласования выходной нагрузки R e , когда в выражении (2) Г _н = 0, уравнение (3) при Z _bx ( fk ) = Zk ( fk ) запишем следующим образом:

,     Zk ( fk ) - Г к

S I =               ,

Zk ( fk) + Г к

где * – знак комплексного сопряжения.

Учитывая выражение (4), а также то, что ^ 22 = 0, так как в рассматриваемой на рис. 1 модели R _E является чисто активной величиной, перепишем уравнение (1) в новом виде:

^2ф“⁽ fk ) = ^arctgR | ;

+ П =

= arctg Im

Zk ( fk ) - Г к ) /_Re ^f Zk ( fk ) - Г к Zk ^{( f}k ) ^{+ Г} к )! I Zk ^{( f}k ) ^{+ г} к

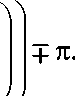
Уравнение (5), которое получено на основе условия унитарности [S]-матрицы выходной цепи устройства класса Е на рис. 1, представляет собой аргумент коэффициента передачи S ₁₂ выходной цепи (или ее фазочастотные характеристики на любой k -й гармонике) в виде функции импеданса нагрузки ключа Z_k ( f_k ) на основной частоте и ее гармониках, а также как зависимость от существенно нелинейного активного сопротивления r _к ключа, работающего принципиально в двух состояниях,

соответствующих либо нулевому, либо бесконечному сопротивлению.

Импедансы нагрузок ключа Z_k ( f_k ) для четырех известных усилителей мощности класса Е и дуальных им устройств сведены в таблицы, которые опубликованы в монографиях [5; 6]. Для одной выбранной среди таких усилителей пары рассмотрим в качестве примера их характеристики Z_{k и}( f_k ) и Z_k ( f_k ), представленные в таблице. В отличие от дуального устройства в исходном усилителе эти импедансы снабжены в таблице дополнительным индексом «и». Для обоих типов устройств в таблице приведены также их электронные КПД, которые рассчитаны в работах [5; 6] при различных числах k используемых гармоник. Очевидно, что в усилителях мощности Е-класса 100%-ный электронный КПД имеет место, если в их работе принимает участие максимальное число гармоник k ^ to . Используя табличные данные в выражении (5) для каждого из условий г _к = 0 и г _к = to , одновременно оценим поведение фазочастотных характеристик выбранных устройств Е-класса.

Для рассматриваемой пары усилителей Е-класса нетрудно установить, что при любых значениях Z_k ( f_k ) (или Z_{k и}( f_k )) в таблице и работе всех их ключей в двух состояниях, когда Г _к = 0 и Г _к = to , справедливо приближенное равенство

Ф 12 ( fk ) ~ ⁰ ± ^{п (6)}

Более того, можно показать также, что уравнение (6) выполняется и для других отмеченных в [5; 6] дуальных пар усилителей мощности Е-клас-са. При помощи равенства (6) дается оценка величины фазы коэффициента передачи на любой гармонике основной частоты для показанной на рис. 1 модели устройства, работающего в режиме Е-класса. Очевидно, если в этой модели учесть для реальных транзисторов избыточную величину их выходной емкости, которая превышает расчетное для Е-класса значение, то в уравнении (6) фазовые длины Ф 12 на гармониках могут отличаться от нуля или от величин ±п . Необходимость выполнения условия (6) является основанием для коррек-

Таблица. Электронные КПД и нагрузочные импедансы ключей дуальной пары усилителей мощности Е-класса Table. Electronic efficiency and load impedances of switches of a dual pair of class E power amplifiers

Номер гармоники	Нормированные импедансы нагрузок ключа в исходном усилителе класса Е	Нормированные импедансы нагрузок ключа в дуальном усилителе класса Е	Электронные КПД дуальной пары усилителей класса Е
k	Zk и при R Еи = 1	Zk при R Е = 1	КПД, %
1	1,527 + j 1,106	0,429 – j 0,311	7,9
2	– j 2,723	j 0,367	66,6
3	– j 1,816	j 0,551	75,6
4	– j 1,361	j 0,735	83,8
5	– j 1,089	j 0,918	86,3
6	– j 0,908	j 1,102	89,5
7	– j 0,778	j 1,285	90,6
8	– j 0,681	j 1,469	92,4
9	– j 0,605	j 1,652	92,9
10	– j 0,545	j 1,836	94
k ^ «	_ nn 2 + 4) R EH Xk ■ =    - 8 k	8 kR Хь =E— n ( n 2 + 4)	100

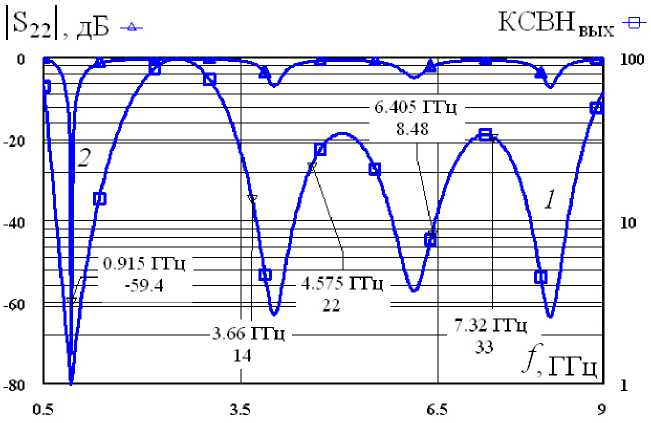
Рис. 2. Зависимости КСВН_вых (кривая 1) и модуля коэффициента отражения на выходе |S₂₂| (кривая 2) от частоты Fig. 2. Dependences of VSWR_out (curve 1) and module of reflection coefficient at the output |S₂₂| (curve 2) on frequency

ции известных методик проектирования выходных цепей устройств Е-класса [5; 11]. Например, в усилителях мощности Е-класса кроме реализации табличных значений нагрузок ключей на основной частоте и ее (в идеале – всех) гармониках эти методики необходимо дополнить введением более «тонкой настройки» разрабатываемых выходных цепей. Данная настройка заключается в выборе параметров элементов выходных цепей, где в наибольшей степени соблюдается равенство (6) при использовании максимально возможного числа гармоник k .

Для подтверждения сделанных на основе равенства (6) выводов используем экспериментальные результаты, которые получены в работе [5] для исходного усилителя мощности Е-класса с такими же, как в таблице, импедансами нагрузок ключей. Рассмотрим тот же макет усилителя мощности, который разработан на транзисторе FLL120MK с минимальной выходной емкостью 6,5 пФ. Используя рекомендации книги [12], получим для рассматриваемого усилителя Е-класса его частотные зависимости выходных КСВНвых и модуля коэффициента отражения |S22|. Одновременно с

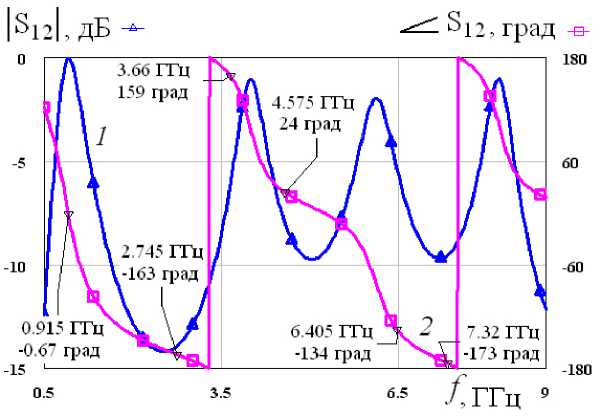
Рис. 3. Амплитудно-частотная |S 12I (кривая 1) и фазочастотная Z 5 12 (кривая 2) характеристики выходной цепи Fig. 3. Amplitude-frequency |S 12 | (curve 1) and phase-frequency Z 5 ₁₂ (curve 2) characteristics of the output circuit

этим проведем оптимизацию фаз коэффициентов передачи выходной цепи усилителя на гармониках. Регулируя параметры элементов выходных цепей данного усилителя, эти фазы в соответствии с уравнением (6) оптимизируются на каждой из гармоник при максимально возможном числе k . В результате для такого усилителя одновременно получены на рис. 2 зависимости КСВН_вых( f ) (кривая 1) и |S₂₂|( f ) (кривая 2), а также на рис. 3 – амплитудно-частотная |S₁₂|( f ) (кривая 1) и фазочастотная Ф 12 ( f ) = arg 5 12 ( f ) (кривая 2) характеристики.

Из приведенных на рис. 2 графиков видно, что на рабочей частоте 915 МГц имеет место практически идеальное согласование импеданса Z 1 ( f 1 ) с трактом на выходе 50 Ом, так как |S₂₂| = –59,4 дБ. Более того, до восьмой гармоники включительно КСВН_вых > 8,5. При выбранных в усилителе структуре и параметрах элементов выходной цепи такие высокие значения КСВН_вых свидетельствуют о режимах «холостого хода», которые реализуются на его гармониках. Кроме того, частотные зависимости на рис. 2 практически совпадают с аналогичными зависимостями, которые получены в работах [5; 11].

Приведенная на рис. 3 амплитудно-частотная характеристика усилителя подтверждает его идеальное согласование на основной частоте. Вместе с тем из анализа фазочастотной характеристики выходной цепи усилителя следует, что значения фаз на тех же, что и на рис. 2, частотах гармоник близки к нулевым величинам или значениям ±п. Это подтверждает теоретические выводы, кото- рые сделаны на основе полученных выше уравнений (5) и (6). Однако некоторые отклонения (особенно на частотах высших гармоник) фаз ф^ (fk) от теоретически установленных пределов связаны, очевидно, с тем, что избыточные величины выходной емкости выбранного СВЧ-транзистора проявляются в большей степени именно с ростом k.

Заключение

Таким образом, для устройства Е-класса на основе унитарности [S]-матрицы его выходной цепи дана оценка аргументов ее коэффициентов передачи на любой гармонике основной частоты. Получены формулы (5) и (6) для приблизительных фазочастотных характеристик модели устройства Е-класса с ключом, который работает в двух состояниях, соответствующих его нулевому и бесконечному активным сопротивлениям. На примере представленных фазочастотных характеристик разработанного в [5; 11] макета усилителя мощности Е-класса подтверждена справедливость приблизительного равенства (6). С учетом следующих из выражений (5) и (6) выводов сформулированы рекомендации для внесения дополнений в известные методики проектирования устройств Е-клас-са [5; 6; 11]. Данные методики можно дополнить введением настройки параметров элементов выходных цепей, для которых в наибольшей степени соблюдается равенство (6) при использовании максимально возможного числа гармоник k .