Оценка фирмы: налоговые щиты и ставки дисконтирования

Определение рыночной стоимости фирмы дисконтированием денежных потоков проводится на базе выбранного денежного потока и ставки дисконтирования для него. Денежные потоки фактически являются будущими ожидаемыми учетными (accounting) результатами, а вот ставки дисконтирования должны рассчитываться на основе рыночной (market) стоимости элементов баланса, что и позволяет определять текущую рыночную стоимость (market value) фирмы.

Различают два способа создания фирмой стоимости акционеров (shareholders value):

• •    операционное создание стоимости – ведение бизнеса таким образом, чтобы операционная прибыльность превышала бизнес-риск;

• •    финансовое создание стоимости – использование стратегий финансирования, удерживающих прибыль внутри фирмы за счет налоговых щитов.

DCF-модели (Discounted Cash Flow, модели дисконтированного денежного потока) нацелены на фиксацию процесса создания стоимости акционеров для того, чтобы выявить реальную стоимость фирмы – рыночную стоимость, которая определяется с обеих сторон «рыночного» баланса:

V_U + V_TS = E + D ,                                                                       (2.1) ²

где V_U – рыночная стоимость «бездолговой» фирмы;

• V_TS – рыночная стоимость налоговых щитов;

E – рыночная стоимость собственного (акционерного) капитала;

D – рыночная стоимость долга.

Из формулы (2.1) можно определить сразу несколько фундаментальных отношений между рыночными элементами и их ставками дисконтирования:

V U – D = E – V TS ;

(2.2)

(2.3)

V U – E = D – V TS .

Из выражения (2.3) при D > 0 следует:

* полный оригинальный текст настоящей работы находится в постоянном доступе (адрес: abstract=1610143). Публикация представленного в статье материала осуществляется с согласия автора. Перевод выполнил Лаврентьев Михаил Викторович – оценщик Института проблем предпринимательства, член ассоциации «СРОО «Экспертный совет» (г. Санкт-Петербург),

D >  V TS ;

(2.4)

(2.5)

V U >  E .

Обращаясь к ставкам дисконтирования, отметим, что акционеры подвергаются большему риску, чем кредиторы, поскольку дивиденды выплачиваются после процентов по кредитам, тем более при банкротстве:

K_E >  K_D ;                                                                                      (2.6)

K_E >  K_U ,                                                                                      (2.7)

где K_U – ставка для собственного капитала «бездолговой» фирмы;

K_E – ставка для собственного капитала «долговой» фирмы;

K_D – ставка для заемного капитала (долга).

Выражение (2.7) выполняется, поскольку K_U учитывает только бизнес-риск, а K_E – еще и риск финансирования.

Отношение (2.1) верно, если взвесить рыночные элементы по рыночной стоимости фирмы V и применить к ним соответствующие ставки дисконтирования:

K0VU + KTSVTS = KEE + KDD,(2 8)

UVTSVEVDV(2.8)

где V – рыночная стоимость фирмы;

K_TS – ставка для налоговых щитов.

Из формулы (2.8) получаем:

Ku x Vu + Kts x Vts = Ke x E + Kd x D•(2.9)

Из формулы (2.9) с учетом, что V_U = E + D - V_TS , получаем:

K e = K u + ( K u — K d ) D " ( K u — K ts ) V S •                                         (2.10)

Из формулы (2.10) можно выразить ставку К_Е как растущую функцию отношения D / E :

K e = K u + ^ K u —

^KD ^{+( K}U  ^KTS ) D

D

E"

(2.11)

Также вспомним «классическую» формулу средневзвешенной стоимости капитала:

(2.12)

WACC = KE—— + KD (1- T ——, EE + D D(   ) E + D где WACC – средневзвешенная стоимость капитала;

τ – номинальная ставка налога на прибыль.

Все приведенные выражения выводятся напрямую из формул, указанных в работе [9], и выполняются всегда независимо от допущений относительно D , V_TS и K_TS .

Будем понимать приведенные отношения как стандартные, поскольку фундаменталь- ное равенство рыночных стоимостей актива и пассива баланса показанное в работе [9], – это ключ к модели, описанной в настоящей работе.

Особенности традиционных подходов к построению DCF-моделей

В своей первой работе [1] Модильяни и Миллер пришли к выводу, что в условиях отсутствия налогов стоимость фирмы не зависит от левереджа. Во второй работе [2] они учли существование налогов и налоговых щитов. С тех пор вышло много работ, посвященных оценке фирм дисконтированием денежных потоков (см. [3–6]), однако они не согласуются между собой прежде всего в допущениях относительно ставки дисконтирования для налоговых щитов и уровня долга.

Авторы работы [2] основывались на следующих допущениях:

• •    уровень долга D постоянен;

• •    риск налоговых щитов равен риску долга ( K_TS = K_D );

• •    стоимость долга постоянна.

В этих жестких условиях текущая стоимость налоговых щитов тоже постоянна и не зависит от стоимости долга ( V TS = т * D ).

Майлз и Иззел (см. [4]) предложили модель, в которой фирма ежегодно реновирует долг, поддерживая постоянным коэффициент левереджа D / V . В этой модели в первый год риск налоговых щитов равен стоимости долга ( K_TS = K_D ), а в последующие годы он следует за риском бизнеса ( K_TS = K_U ), поскольку левередж изменяется так же, как стоимость фирмы. Стоимость долга постоянна.

Харрис и Прингл (см. [5]) развили теорию постоянного левереджа, рассмотрев непрерывную ребалансировку долга. В их допущениях риск налоговых щитов равен риску собственного капитала «бездолговой» фирмы ( K_TS = K_U ).

Однако такие детерминированные стратегии финансирования вряд ли могут быть в реальности. Более того, авторы работ [2, 5] не учитывают следующие соображения:

• •    полагать, что K_E , K_D , K_TS и WACC являются постоянными, вряд ли разумно, поскольку финансовый риск, влияющий на них, очевидно меняется с левереджем;

• •    моделирование налоговых щитов в виде TS t = т х ( K_D х D ) t фактически означает их реализацию без отсрочек. Однако в жизни фирмы часто фиксируют в учете убытки, откладывая реализацию налогового щита;

• •    DCF-модели, по сути, итеративны – рыночная стоимость компонентов баланса определяется на основе рыночных ставок дисконтирования, и наоборот. Чаще всего эту проблему обходят принятием целевых уровней для долга, а в качестве примеров берут простейшие «вечные» модели.

В настоящей статье предлагается новая DCF-модель, при использовании которой становится возможным преодолеть все описанные сложности, поскольку эта модель:

• •    основана на фундаментальном равенстве сторон «рыночного» баланса, как это описано в работе [9];

• •    эндогенизирует стоимость долга как функцию левереджа по аналогии с подходом, описанным в работе [7];

• •    на основе равенства сторон «рыночного» баланса и портфельной теории выводит общее выражение для ставки дисконтирования налоговых щитов;

• •    использует возможности современных табличных процессоров для преодоления проблемы итеративности (подробнее см. [8]).

Допущения

В настоящей работе предполагаются постоянными безрисковая ставка R_F , ставка налога на прибыль τ и ставка для собственного капитала «бездолговой» фирмы K_U , измеряющая операционный риск фирмы. Эти допущения намного мягче и реалистичнее принятых в большинстве существующих моделей.

Все остальные ставки ( K_D, K_TS и K_E ) подразумеваются свободно изменяющимися с левереджем, без введения каких-либо ограничений на структуру капитала.

Рыночная стоимость долга предполагается равной учетной, кроме случаев, когда долг настолько велик, что проценты превышают операционный результат. Другими словами, полагается, что долг фирмы не торгуется на финансовом рынке. Это непринципиальное упрощение подразумевается и во всех прочих моделях.

Также констатируется, что кредиторы не претендуют на прибыль фирмы, которая полностью достается акционерам.

И наконец, предполагается возможность существования отложенных убытков и, соответственно, отложенных налоговых щитов.

«Рыночный» баланс: новый анализ

Обращаясь к «рыночному» балансу, важно заметить, что текущей стоимости налоговых щитов ( V_TS ) в активе баланса должен быть эквивалент в пассиве баланса. Поскольку налоговые щиты порождаются долгом, но целиком достаются акционерам, разделим рыночную стоимость собственного капитала на стоимость собственного капитала без налоговых щитов и стоимость налоговых щитов:

E = ( E – V TS ) + V TS ;

(4.2)

(4.3)

V U + V TS = ( E – V TS ) + V TS + D .

Из выражения (2.9) следует, что для элемента ( E - V_TS ) должна существовать такая ставка дисконтирования K_{E – VTS} , что (2.9) может быть переписано в виде:

K u ^x V u + K ts ^x V ts = K e - vts ^x ( E — V ts ) + K ts ^x V ts + K d ^x D ,                           (4.4)

где K_{E – VTS} – ставка дисконтирования для элемента ( E - V_TS ).

Ставка K_{E – VTS} может пониматься как ставка дисконтирования для собственного капитала при игнорировании существующих налоговых щитов.

На основе портфельной теории можно записать:

К           E  V^TS      V TS.

(4.5)

K E   K E - VTS    e K TS e "

Важно понимать, что K_{E – VTS} отличается от K_U . Действительно, K_{E – VTS} учитывает увеличение финансового риска (и, соответственно, отдачи, требуемой акционерами), обусловленное долговым финансированием, а K_U нет. Можно полагать, что K_{E – VTS} >  K_E , поскольку предполагается, что налоговые щиты не попадут к акционерам и не компенсируют риск долгового финансирования.

«Рыночный» баланс без стоимости налоговых щитов

Вычтем из обеих частей баланса рыночную стоимость налоговых щитов. Из выражений (4.3) и (4.4) получим отношения, не зависящие от ставки K_TS :

V U = ( E – V TS ) + D ;

K u ^x V u = K e - VTS ^x ( E - V ts ) + K d ^x D .

(4.6bis)

(4.6)

Поскольку K_U предполагается постоянной, уже сейчас можно определить рыночную стоимость «бездолговой» фирмы:

^

V u = 2 t = 1

FCFt

(1 + K u ) t ,

(4.7)

где FCF – свободный денежный поток на инвестированный капитал; t – временной индекс.

Ставка для собственного капитала при игнорировании налоговых щитов

Как мы уже отмечали, K_{E – VTS} может пониматься как ставка дисконтирования для собственного капитала при игнорировании налоговых щитов. Из выражения (4.6) следует:

K e - vts = K u + ( K u - K d ) ^—.                                             (4.8)

^E V TS

Для самопроверки подставим формулу (4.8) в выражение (4.5) и получим (2.10). Также стоит отметить, что (4.8) больше (2.10), то есть K_{E – VTS} >  K_E . Рыночная стоимость элемента ( E - V_TS ) определяется на основе денежного потока ( ECF - TS ):

_ ^ ECF t - ^TSt

E VTS   ^ ,             xt , t=1 (1 + Ke -vTSt )

(4.10)

где ECF – денежный поток на собственный капитал; TS – денежный поток для налоговых щитов.

Из выражений (2.2) и (4.8) следует:

K E - VTS = ^Ku ^{+ ( K}u  ^Kd ) ,,   _п

V, - D

(4.11)

Последнее выражение примечательно тем, что оно не зависит от K_TS .

Стоимость долга

Минимальный процент по кредиту равен безрисковой ставке. Отталкиваясь от кредитоспособности и уровня левереджа фирмы, кредиторы добавят к безрисковой ставке кредитную премию. Таким образом, стоимость долга равна:

K d = R f + ( K u - R f ) x ( D / V u ) n ,

(4.12)

где R_F – безрисковая ставка;

n – маржинальный фактор кредитного риска.

Начальный уровень стоимости долга равен безрисковой ставке R_F . С увеличением объема долга его стоимость увеличивается на кредитную премию ( K_U – R_F ), умноженную на коэффициент левереджа D / V_U . Показатель степени n назовем маржинальным фактором кредитного риска.

Когда размер долга возрастает до такой степени, что D / V_U приближается к 1, кредиторы фактически становятся акционерами и несут риск бизнеса фирмы K_U .

Отношение (4.12) ценно тем, что принимает во внимание основные параметры, на которые ориентируются кредиторы в процессе вынесения кредитных решений:

• •    начальная кредитоспособность оценивается посредством K_U . Чем выше бизнес-риск фирмы, тем больше премия ( K_U – R_F ) и, соответственно, K_D ;

• •    прибыльность конкретной компании по сравнению с другими компаниями сектора отражена в V_U . Действительно, если отдача инвестированного капитала превышает K_U , то V_U больше своей учетной стоимости, что уменьшает коэффициент D / V_U и, соответственно, величину K_D . То есть когда кредиторы видят меньший риск дефолта, они назначают более низкие ставки по кредитам;

• •    поскольку левередж представлен как D / V_U , то при постоянной V_U чем выше объем долга D , тем выше его стоимость K_D .

С учетом сказанного значение V_U можно интерпретировать как ключевой элемент для составления кредитных рейтингов.

Важно, что левередж входит в модель стоимости долга в виде D / V_U , а не D / V (ср., например, с подходом, представленным в работе [7]), поскольку налоговые щиты реализуются только акционерами, а не кредиторами. Отметим, что при D = V_U имеем K_D = K_U , E = V_TS , а чистая прибыль и налоговый щит равна EBIT х (1 - т ) х _т (здесь и далее традиционно EBIT – прибыль до вычета процентов и налогов, EBT – прибыль до вычета налогов).

Маржинальный фактор кредитного риска n не следует путать с маржинальной стоимостью долга, равной первой производной стоимости долга по его размеру. Логика моделирования K_D требует, чтобы последняя была строго непрерывной и растущей функцией размера долга, что выполняется для любых n ≥ 1.

Рассмотрим три значения n :

• 1)    базовая линейная форма n = 1. Стоимость долга линейно возрастает с левереджем, но маржинальная стоимость долга постоянна;

• 2)    случай целого и постоянного n > 1. Очевидным решением является n = 2. В этом случае стоимость долга с ростом левереджа возрастает более чем линейно, но маржинальная стоимость долга с левереджем увеличивается лишь линейно, а не экспоненциально.

Если использовать большие значения для n , то выражение (4.12) при D / V_U ≈ 1 дает неадекватные цифры из-за того, что вариация D / V_U предполагается в диапазоне от 0 до 1, так что результат возведения небольших («нормальных») значений D / V_U в большие степени стремится к нулю. Но в любом случае использование 1 <  n ≤ 3 намного больше соответствует реальности, чем принятие n = 1;

• 3)    помимо постоянных значений для n , рассмотрим вариант, когда маржинальный фактор кредитного риска является функцией левереджа:

n = 1 + f ( D / V_U ).                                                                               (4.26)

С алгебраической точки зрения это наиболее сложные случаи, но для них все еще воз- можно вычислить маржинальную стоимость долга, которая с ростом левереджа возрастает экспоненциально. Такая модель стоимости долга видится наиболее приближенной к реальности.

«Оптимальный» уровень долга

Все еще не зная ставки дисконтирования для налоговых щитов K_TS , все-таки можно определить такой «оптимальный» уровень долга D ^* , который максимизирует рыночную стоимость фирмы.

Действительно, при уровне долга D ^* максимизируется текущая рыночная стоимость налоговых щитов V_TS безотносительно ставок дисконтирования для них. Такая максимизация налоговых щитов происходит, когда фирма не платит налога на прибыль, потому что весь операционный доход идет на уплату процентов по кредиту ( EBIT = K D х D и EBT = 0). В этом случае фирма фактически полностью профинансирована за счет заемного капитала ( E = 0), и кредиторы здесь фактически становятся акционерами. В реальности такое 100-процентное долговое финансирование, скорее всего, невозможно, но в теории эту задачу стоит решить.

Сказанное можно записать так:

V max = D *= V u + V tT ,                                                            (4.28)

где V_MAX – максимальная рыночная стоимость фирмы;

• D ^* – «оптимальный» уровень долга;

V_T^M_S^AX – рыночная стоимость налоговых щитов при «оптимальном» долге.

Для того чтобы найти «оптимальный» уровень долга D ^* и предполагая EBIT > 0, нужно решить уравнение:

EBIT - K D х D = 0.                                                               (4.29)

Подставляя выражение (4.12) в (4.29), получаем:

D^{n +}1 ⁽ K U -R ) + D ^x R F - EBIT = 0.                                            (4.30)

Это уравнение является единственным условием теоретической максимизации рыночной стоимости фирмы независимо от значений n и K_TS .

Определив из формулы (4.30) величину D ^*, из формул (4.29) и (4.11) можно сразу получить:

K_D* = EBIT / D ^* ;                                                                         (4.35)

K = K. + ( K y - K_n.) D _t .                                                     (4.36)

( E - VTS )      ^{U U} D V^ _— D *

Заметим, что выражения ( K_U - K_D ) и ( D - V_U ) в (4.36) меняют знак одновременно, поскольку при D = V_U справедливо K_D = K_U . Таким образом, K_{E – VTS} является строго растущей функцией D , что обеспечено корректным моделированием K_D .

Исходя из сказанного в дальнейшем будем различать два случая:

• 1)    полная (сильная) максимизация: D / V = 1;

• 2)    простая (слабая) максимизация: D / V_U = 1.

Что произойдет, если учетная стоимость долга превысит рыночную стоимость фирмы? В этом случае K_D >  K_D* , и операционного результата не хватит на выплату всех процентов по кредитам. Если такое положение дел будет постоянным, то это определенно уменьшит рыночную стоимость фирмы. Итак, в рассматриваемом случае рыночная стоимость долга не равна учетной, она уменьшается на ту же величину, что и рыночная стоимость фирмы:

(4.39)

D t = min ( D BOOK t , V t ), где D – рыночная стоимость долга;

D_BOOK – учетная стоимость долга;

V – рыночная стоимость фирмы; t – временной индекс.

Ставка для налоговых щитов

Ставка дисконтирования налоговых щитов K_TS имеет свое собственное выражение, отличное от рассмотренных ранее.

Поскольку налоговые щиты порождаются долговым финансированием, вряд ли их риск будет меньше риска порождающего их долга, поэтому можно полагать, что начальный уровень K_TS равен начальному уровню риска долга (когда долга нет), то есть при D = 0 имеем K_TS = K_D = R_F .

Как уже отмечалось, условие K_{E – VTS} >  K_E должно выполняться всегда. То есть используя определения этих ставок (2.10) и (4.8) и полагая D > 0, имеем:

(4.40)

^KU ^{+ ( K}U - ^KD ) E - V >  ^KU ^{+ ( K}U - ^KD ) E - ^{( K}U - K TS ) -^E .

Выразим K_TS из (4.40), полагая, что E > 0 и V_TS > 0 (это равносильно тому, что 0 <  D <  V или D / V < 1). После преобразований получим, что при этих условиях K_TS <  K_{E – VTS} . Полагая, что E < 0 (то есть при D / V > 1), получим K_TS >  K_{E – VTS} . Наконец, поскольку K_{E – VTS} определена при E = 0 и K_TS должна быть непрерывной функцией, при E = 0 (то есть при D / V = 1) должно быть K_TS = K_{E – VTS} .

Обращаясь к выражению (4.5), можно заметить, что при D / V_U = 1 (что подразумевает V_TS = E ) получается K_E = K_TS <  K_{E – VTS} .

К этому моменту о ставке для налоговых щитов K_TS известно следующее:

K_TS = K_D при D = 0;

K_TS <  K_{E – VTS} при D / V < 1;

K_TS = K_E при D / V_U = 1;

K_TS = K_{E – VTS} при D / V = 1;

K_TS >  K_{E – VTS} при D / V > 1.

На основе этого будем моделировать ставку K_TS следующим образом:

K TS = K D ^{+ (} K E - VTS   K D ) V ■

(4.44)

Из выражения (4.44) видно, что KTS является возрастающей функцией левереджа D / V, ее начальное значение равно стоимости долга KD, а со стремлением левереджа к 1 она стремится к уровню ставки KE – VTS – отдаче, которую требуют акционеры при условии, что они не получают выгоды от долговых налоговых щитов. Если уровень долга превышает величину D*, за которой операционных результатов не хватает на оплату процентов по кредитам, величина KTS превышает величину KE – VTS.

Выражение (4.44) экономически обосновано в том же смысле, что и выражения для прочих ставок дисконтирования, полученные в настоящей работе. Согласно выражению (4.44) величина K_TS зависит:

• •    от операционного результата фирмы: чем выше EBIT , тем ниже стоимость долга K_D , ставка K_{E – VTS} , левередж D / V , и, следовательно, K_TS , поскольку V_U растет;

• •    от размера долга: чем выше долг D , тем выше стоимость долга K_D , ставка K_{E – VTS} , левередж D / V и, следовательно, K_TS ;

• •    от стоимости долга: чем выше стоимость долга K_D , тем выше K_TS , поскольку увеличение K_D превышает снижение отношения ( K_{E – VTS} - K_D ) / ( D / V ).

Более того, как и следовало ожидать, для любого «разумного» уровня долга (0 <  D <  V_U ) величина K_TS лежит между K_D и K_E . Случай D >  V_U вряд ли может произойти в реальности и интересен, скорее, с теоретической точки зрения.

Выражение (4.44) требует только допущения о фундаментальном равенстве актива и пассива «рыночного» баланса. Оно справедливо для любого уровня долга и не требует фиксации ни D , ни D / V . Как любая другая ставка, K_TS может изменяться в зависимости от размера долга и операционных результатов фирмы.

И наконец, выражение (4.44) не требует даже эндогенизации стоимости долга (как это сделано здесь) и может быть выведено даже при допущении о неизменяемости последней. Это следует отметить, чтобы сравнить полученные результаты с распространенными моделями (см. [2, 5]).

Модификация денежного потока для налоговых щитов

При прочих равных условиях налоговый щит не может превышать величину EBIT х т , в то время как проценты по кредитам K D х D могут неограниченно возрастать с левереджем. То есть при K D х D = EBIT + е фактический налоговый щит по-прежнему равен EBIT х т , в то время как «классический» расчет дает:

( K D х D ) х т = ( EBIT + е ) х т = EBIT х т + е х т . (4.45)

Величина е х т относится в будущее в качестве налогового вычета. Она будет реализована так скоро, как можно будет найти такой год (или несколько лет) x = t + 1, …, m , причем x = m – последний год, при котором выполнится следующее условие:

m

! [ EBIT - ( K_D х D ) x ] т = S t .

(4.46)

x = t + 1

Модифицируем расчет денежного потока налоговых щитов с учетом сказанного. Для этого добавим в отчет о прибылях и убытках три показателя:

LCF_t = max [( K_D х D ) _t - EBIT t , 0]; (4.47) ALCF_t = ALCF_{t - 1} + LCF_t – max [( EBIT_{t - 1} - TI_{t - 1} ), 0]; (4.48) TI_t = max [( EBT_t – ALCF_t ), 0], (4.49) где LCF_t – отложенный убыток (Loss Carried Forward);

ALCF_t – накопленный отложенный убыток (Accumulated LCF);

TI_t – налогооблагаемый доход (Taxable Income); t – временной индекс.

Тогда реальные налог на прибыль и налоговый щит в году t равны:

(4.50)

(4.51)

I t = TI t ^x T ;

TSt = EBITt x T - It, где It – налог на прибыль;

TS_t – денежный поток для налоговых щитов.

Приведение полученных выражений к единообразному виду

Приведем полученные ранее выражения для K_D , K_{E – VTS} и K_TS к единообразному виду, то есть выразим их через R_F и K_U .

Очевидно, что выражение (4.12) является в этом смысле наиболее компактной формой для стоимости долга K_D .

Обращаясь к ставке K_{E – VTS} , из выражений (4.8), (2.2) и (4.12) получаем:

K E - VTS

= K U + ( K U

-

^RF )

⎛ V_Uⁿ - Dⁿ ⎞ D

. ^⎜⎝ V U - D ^⎟⎠ V U ⁿ

(4.52)

Итак, ставка K_{E – VTS} (как и K_D ) является функцией коэффициента левереджа D / V_U . Это соответствует определению K_{E – VTS} , поскольку она применима для денежного потока на собственный капитал без учета налоговых щитов. Таким образом:

(4.52bis)

max ( E – V_TS ) = V_U .

Из формулы (4.52) видно, что при n = 1 получаем ( V_Uⁿ - Dⁿ ) / ( V_U - D ) = 1, из чего следует, что и K_D , и K_E-VTS линейно и одинаково растут с левереджем и различаются только начальным риском ( R_F и K_U соответственно). При n > 1 выражение (4.52) не определено для D = V_U (этот случай будет рассмотрен далее).

Обращаясь к ставке для налоговых щитов K_TS , из выражений (4.44), (4.12) и (4.52) получаем:

K TS

= K D + ( K U

-

^RF )

V U ⁿ

-

Dⁿ ⎞⎛ V_U

A

D

V U

-

D

Vⁿ ⎠⎝ U ⎠

V

.

(4.53)

Здесь K_TS все еще выражена через коэффициент общего левереджа D / V , что логично, поскольку риск налоговых щитов относится ко всей фирме целиком, а не только к ее операционной деятельности.

Для рыночной премии ( K_{E – VTS} - K_D ) из формулы (4.52) известно, что K_D и K_{E – VTS} линейно и одинаково растут с левереджем при n = 1. Выразим эту премию из формулы (4.53) и получим:

K E - VTS ^- K D ⁼ ( K U

-

^RF )

⎛ V U ⁿ - D ⁿ ⎞⎛ V U ^⎜⎝ ^VU ^{- D ⎟}⎠^⎜⎝ ^VU ⁿ

⎞⎟ ⎠

(4.54)

Выражение (4.54) подтверждает, что при n = 1 премия ( K_{E - VTS} - K_D ) постоянна и равна

( K_U - R_F ). Таким образом, из (4.44) видно, что при n = 1 риск налоговых щитов K_TS является строго растущей функцией левереджа.

Для нелинейных случаев ( n > 1 для любого уровня долга D ) можно показать, что премия

( K_{E – VTS} - K_D ) также является строго растущей функцией левереджа, а ставка K_TS в этом случае – тем более.

Осталось рассмотреть случай D = V_U . При этом уровне долга при n > 1 выражения (4.52), (4.53) и (4.54) не определены. Избавляясь от неопределенности, получаем:

V_Uⁿ - Dⁿ V U - D

= nV U ^{n - 1}.

(4.59)

Подставив (4.59) в формулу (4.54), имеем:

K e - vts — K d = ( K u — R f ) ^X n •                                                             (4.60)

Это согласуется с уже оговоренным случаем n = 1. Подставив (4.60) в формулу (4.53), получим:

K ts = K d + ( K u - R f ) x n x ( D / V) .

(4.61)

Поскольку D = V_U и, следовательно, K_D = K_U , то выражение (4.61) может записать так:

K ts = K u + ( K u — R f ) x n x ( V u / V) .                                                      (4.62)

Подставив (4.59) в формулу (4.52) с учетом D = V_U , получим:

K e - vts = K u + ( K u — R f ) x n .                                                              (4.64)

Итак, при n > 1 премия ( K_{E – VTS} - K_D ) является строго возрастающей функцией левереджа D / V , что, в свою очередь, делает зависимость ставки для налоговых щитов K_TS от левереджа даже более чем линейной. Более того, при n ≥ 1 ставки K_D , K_TS и K_{E – VTS} являются строго непрерывными и растущими функциями левереджа, что и следовало ожидать с теоретической и экономической точек зрения.

И наконец, подставив (4.12) в (4.53), можно получить наиболее «стандартное» выражение для ставки налоговых щитов:

K TS = R F + ( K U - R F )

⎛ D ^⎜⎝ V U

n ⎞_⎟ ⎠

V U ⁿ - Dⁿ ⎞⎛ V U

^VU ^{- D ⎟}⎠^⎜⎝ ^VU ⁿ

^⎞⎟ _V ^D ⎠

(4.67)

Ставка для собственного капитала

Ранее для ставки дисконтирования для собственного (акционерного) капитала фирмы K_E были получены лишь общие выражения (2.10) и (4.5) и сопоставлены K_E и K_{E – VTS} при выводе формулы ставки для налоговых щитов K_TS .

Это обусловлено тем, что ставка K_E наиболее сложна для анализа и в целом не определяется «сама по себе», поскольку она одновременно зависит от всех рассмотренных факторов, а именно:

• •    операционная прибыльность фирмы EBIT , отражаемая в V_U ;

• •    размер долга D и его стоимость K_D ;

• •    операционный риск сектора деятельности фирмы K_U ;

• •    стоимость налоговых щитов V_TS , которая компенсирует акционерам часть финансового риска, порождаемого долговым финансированием.

Итак, построение модели ставки K_E требует довольно громоздких выражений, при этом для нее не получается построить «стандартное» выражение, подобно таковым для прочих ставок, то есть выражение, включающее начальный риск, какую-либо «рисковую премию» и коэффициент левереджа. В итоге полное раскрытие подстановок выражений для прочих ставок в модели K_E даст только полиномиальные выражения. В связи с этим мы сосредоточимся на экономически значимой группировке факторов ставки K_E .

Начнем с выделения рыночной премии ( K_U - R_F ). Подставив в формулу (2.10) выражения из (4.67) и (4.12), после преобразований получаем:

⎛ nn

K E = K U + ( K U - R F ) ^⎛⎜ ^{V U D}

E ⎛_1- ^V U ^V TS ⎞ V U ^{n ⎜}⎝ VD ^⎟⎠

D

E ^.

(4.68bis0)

Это выражение характерно тем, что оно имеет вид K E = K U + ( K U - R F ) х f( D ), содержит уже знакомое выражение ( V_Uⁿ - Dⁿ ) / ( V_U - D ) и измеряет левередж в виде D / E .

Измеряя левередж через D / E или через D / V , получаем соответственно:

nn

K E = K U + ( K U - R F ) ^⎛⎜ ^{V U D}

nn

K = K + K - R ^{⎛ V U D ⎞} EU ( UF ) ⎜ V _- D ⎟ ⎝ U ⎠

E ⎛ V TS ⎞⎛ E ⎞^⎛ V U ^⎞ _-

_VU n ⎜_{⎝ D} ⎟_⎠⎜_{⎝ V} ⎟_⎠⎜_{⎝ VU} n ⎟_⎠

D

E ^;

V

-

V TS

U

D

V U ⁿ

D

ⁿ ⎠⎝ V U

. V

(4.68)

(4.69)

Для случая n = 1 выражения для K_E сильно упрощаются:

K E = K U + ( K U - R F )

-

V TS

D

V U

D

V

E ^;

⎛

K E = K U + ( K U - R F ) ^⎛⎜ ^V - ^{V TS}

(4.68bis1)

(4.69bis1)

В заключение этого раздела сделаем некоторые замечания.

Стоимость собственного капитала K_E является строго возрастающей функцией левереджа, поскольку дополнительные налоговые щиты компенсируют возрастание финансового риска только частично.

Несмотря на то, что из выражений (4.59) и (4.69) видно, что функция K_E непрерывна в точках D = V_U и E = 0 (то есть при D = D ^* ), с экономической точки зрения нелогично определять стоимость собственного капитала, когда последнего вовсе нет. В любом случае будем считать, что при D = V значения K_E неадекватны.

Рассмотрим разницу между ставками ( K_{E – VTS} - K_E ).

Для начала заметим, что из выражения (4.69) следует:

⎛ ⁿⁿ

K E = K U + ( K U - R F ) ^⎛⎜ ^{V U D}

1-

D

V U V

D _.

V U ⁿ

(4.69bis2)

Стоит отметить, что (4.52) и (4.69bis2) очень похожи: K_{E – VTS} моделируется точно так же, как K_E , но при условии, что V_TS = 0 для любого уровня долга D .

Итак, из формул (4.52) и (4.69bis2) находим:

^KE - VTS ^{- K}E ⁼ ( ^KU

⎛ V ⁿ - D ⁿ ⎞⎛ V ⎞⎛ V ⎞ R UUTS . ^{F )⎜}⎝ V U - D ^⎟⎠^⎜⎝ V U ^{n ⎟}⎠^⎜⎝ V ^⎟⎠

(4.70)

Наконец, из выражений (4.67), (4.69) и (4.59) можно формально доказать ранее высказанную догадку, что при D = V_U будет выполняться K_TS = K_E .

В точке D = V_U также выполняется K_TS >  K_U . Отсюда можно понять, что равенство K_TS = K_U (именно так дисконтируются налоговые щиты в работе [5]) наступит при D <  V_U . Эта мысль будет обсуждена далее.

Сравнение полученных результатов и традиционных подходов

Сравним полученные результаты для ставки K_TS с допущениями, используемыми в других подходах.

Начнем с модели Модильяни и Миллера. Если рассматривать постоянные во времени ставки K TS = K D = R F , откуда следует, что V TS = т х D , то такое допущение переоценивает V_TS , поскольку игнорирует зависимость K_D и K_TS от левереджа и прибыльности фирмы.

Этот случай эквивалентен нашей модели при отсутствии долга, из чего следует, что V_TS = 0. Но поскольку D > 0, это допущение переоценивает V_TS . Действительно, из выражения (4.67) следует, что K_TS систематически недооценивается на следующую величину:

K TS - R F = ( K U - R F )

(4.74)

Если же рассматривать переменные K_TS = K_D , то с учетом формулы (4.12) из (4.67) следует, что в этом случае V_TS все еще переоценены (правда, в меньшей степени), поскольку K_TS систематически недооценивается на следующую величину:

⎛ nn

K - K = K - R^U TS D U F ⎜

V U ⎞ n ⎟

V_U ⎠

D ⎞

. V ^⎟⎠

(4.75)

Можно грубо оценить снижение разрыва ( K_TS - R_F ) в два раза по сравнению со значением, показанным в формуле (4.74).

Перейдем к модели Харриса и Прингла. Рассмотрим случай K_TS = K_U . Выражение (4.67) равно K_U , когда:

Dn

⎛ V U ⁿ - Dⁿ ⎞⎛ V U ^⎜⎝ ^VU ^{- D ⎟}⎠^⎜⎝ ^VU ⁿ

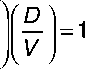
(4.76)

Решая (4.76) относительно долга D , получаем:

D = V u

(-V- [ V + V

U ;

( D / V ) + ( D / V_U ) = 1.

(4.78)

(4.79)

Если выражение (4.79) выполняется в реальности, то оба слагаемых слева очень близки к 1/2. Таким образом, грубо говоря, равенство K TS = — U выполняется, когда фирма примерно поровну профинансирована за счет собственного и заемного капиталов:

( D / V ) = ( D / V U ) = 1/2.                                                                     (4.87)

В этом есть экономический смысл. При D / E < 1 налоговые щиты менее рискованны, чем денежный поток акционеров при D = 0 (поскольку K_TS <  K_U ). Однако при D / E > 1 наблюдается противоположная картина.

Итак, допущения Харриса и Прингла можно использовать для случаев D / E ~ 1. Если D / E < 1, то такое допущение недооценивает текущую стоимость налоговых щитов V_TS . Если D / E > 1, то это допущение переоценивает величину V_TS .

Подводя итог изложенному в этом разделе, отметим, что полагание постоянных K_TS = K_D наиболее ошибочно. Полагание переменных K_TS = K_D все еще переоценивает величину V_TS , но в меньшей степени. Полагание K_TS = K_U не обязательно ведет к ошибкам в оценке V_TS , оно уместно для фирм с постоянным D / E = 1.

Модификация WACC

WACC – это агрегированный показатель, поэтому он не является главным предметом настоящей работы, поскольку здесь выводятся взаимосвязанные определения для всех отдельных ставок дисконтирования. Представим, однако, некоторые соображения относительно WACC и предложим для этого показателя общую формулу, соответствующую идее равенства сторон «рыночного» баланса фирмы.

Известно, что WACC – это рыночная ставка, что означает, что она строится на основе рыночных стоимостей элементов актива и пассива баланса. При этом «классическая» формула WACC (2.12) моделирует вычет процентов по кредиту как — D х D х _т , что является стандартным выражением для учетного денежного потока налоговых щитов. Многие считают непоследовательным использование учетного денежного потока при определении рыночной ставки. С изменением левереджа WACC должна учитывать изменения текущей стоимости налоговых щитов, а не отталкиваться от денежного потока налоговых щитов в конкретный год.

В случае постоянных долга и операционной прибыльности при EBIT >  — D х D имеем:

К _ у Пут

TS = K_D х D х т = — _s х V_TS = K_TS K D ,_XD ^{Л 1} .                                        (4.88)

DTSTSTS

K TS

Поскольку при D > 0 имеем K_TS >  K_D , то из выражения (4.88) следует:

V_TO = — D- т х D < т х D .

(4.89)

TS

K TS

Чем выше левередж, тем больше результат, полученный при решении выражения (4.89), отличается от результата, полученного в допущениях Модильяни и Миллера.

В случае переменной величины долга D формула для «вечности» вообще не выполняется, и «классическая» модель (2.12) смешивает учетный (accounting) денежный поток TS (который может варьироваться и размер которого в конкретный год не обязательно соответствует текущей стоимости налоговых щитов, поскольку размер долга изменяется) и рыночные (market) элементы для собственного и заемного капиталов (Е и D), которые учитывают текущую стоимость налоговых щитов, а не денежный поток для налогового щита конкретного года.

Обращаясь к «рыночному» балансу фирмы, из формул (2.8) и (2.9) можно получить выражения для WACC , содержащие только рыночные элементы:

WACC = K_EE + K_DD - K_7S V S ;

(4.90)

(4.91)

E V D V TS V

UV

Итак, WACC равна бизнес-риску K_U , скорректированному на эффект от долгового финансирования, то есть на выгоды от налоговых щитов.

Заметим, что определение WACC подразумевает построение этой ставки таким образом, что ее использование нецелесообразно для случаев, когда возможны существенные изменения структуры капитала фирмы.

Проиллюстрируем это простым примером. Рассмотрим «вечные» постоянные EBIT = X и FCF = X x (1 - т ). В пассиве баланса фирмы на момент ( t = 0) нет долга, однако на следующий год ( t = 1) фирма хочет получить кредит 0 <  D ₁<  V , порождающий денежный поток для налогового щита TS ₁, который можно представить как долю EBIT , введя такой параметр а , чтобы TS 1 = a x X при 0 <  а <  т . Это подразумевает, что налоговый щит TS 1 будет реализован без отсрочки. Тогда EBT 1 = X x (1 - а / т ) > 0, откуда следует, что налог 1 1 = = EBT 1 x т = X x ( т - а ) > 0. В конце года t = 1 фирма вернет кредит и больше не будет брать в долг.

В этих условиях, реализуя налоговый щит TS ₁, фирма определенно добавит к своей «бездолговой» рыночной стоимости V U = X x (1 - т ) / K U какую-то величину V_TS .

Запишем равенство оценок фирмы методами WACC и APV (Adjusted Present Value):

1- т      1- т      а

(4.93)

-------------------=--1--.

1 + WACC 1  1 + K U 1 + K_TS 1

Введем для целей нашего анализа параметр в такой, что в ^х (1 + K_TS 1 ) = а = TS 1 / X . Теперь выражение (4.93) может быть записано в следующем виде:

1- т _ 1- т

(4.94)

1 + WACC 1 = 1 + K U

Теперь выражение (4.94) не зависит от денежного потока для налогового щита TS ₁. Решая его относительно WACC , получим:

WACC 1 =

K u ( 1 - т ) - в ( 1 + K u ) ( 1 - т ) + в ( 1 + K u )

(4.97)

Из формулы (4.97) можно найти такую величину β , при которой WACC ₁ = 0:

_в = (1 - ^т ) K u 1+ K u

.

(4.98)

Этому значению β соответствует α , равное:

а =

^{1 +} K TS 1

1 + K u

( 1 - т ) K u =

TS 1 K D 1 х D 1 х т

X - X

(4.100)

Значение (4.100) в любом случае весьма мало, вероятно, менее 1/10, поскольку обычно предполагается τ ≤ 1/2, K_U ≤ 1/10 и (1 + K_TS ) / (1 + K_U ) < 2, так что реальный размер долга D ₁ определенно не является экстремальным или незначащим.

Более того, если значение коэффициента β превышает величину (4.98), то WACC ₁ становится отрицательной, что не имеет смысла.

Также нет смысла сдвигать расчет WACC в будущее, поскольку там нет ни денежного потока для налоговых щитов, ни положительных величин V_TS , и, более того, это полностью несовместимо с DCF-методологией.

Таким образом, WACC не используется в примере с полностью стохастическим поведением структуры капитала фирмы, представленном в конце этой работы.

Однако для случая простого постоянного роста вывести внятную формулу для WACC можно. Рассмотрим равенство оценок фирмы методами WACC и APV :

FCF ₁ FCF ₁ TS ₁

(4.101)

WACC - g " K u - g ⁺ K ts - g ’ где g – темп роста.

Решая (4.101) относительно WACC с учетом выражений (4.90) и (4.91), получаем:

WACC = KV + gV TS ;                                               (4.103)

U VV

WACC = K e E + K d-D- - ( K ts - 9 ) V .                                        (4.104)

При g = 0 выражения (4.103) и (4.104) свертываются к полученным ранее выражениям (4.90) и (4.91). При g > 0 и фиксированной структуре капитала выражение (4.88) не выполняется, и «классическая» формула (2.12) не дает тех же результатов, что (4.103) и (4.104), которые верны, так как выведены только из аксиомы (4.101).

Правильность корректировки WACC на g x V_TS / V можно легко доказать. Как следует из (4.101), начальный налоговый щит TS 1 равен ( K_ts - g ) x V_TS . Таким образом, налоговый щит TS 1 меньше «рыночной отдачи налогового щита» K_ts x V_TS , которая была бы получена, если бы «учетный» долг фирмы D_BOOK с самого начала был равен «рыночной» величине долга D . Это «тонкий» момент. Рассмотрим равенство оценок фирмы посредством WACC и ECF :

FCF 1   = ECF i + ( ^Kd ^Х d book ) i

(4.105)

WACC - g K e - g     K d - g

Отсюда получается, что «рыночная» величина долга равна:

D _ ⁽ K D ^X D BOOK ) 1

^KD - g

D BOOK .

(4.106)

В выражении «рыночная величина долга» слово «рыночная» заключено в кавычки, поскольку эта стоимость больше учетной стоимости долга не по причине сверхдоходов или какого-то финансового создания стоимости, а просто потому, что учетная стоимость долга будет возрастать с постоянным темпом g год за годом. Это приведет к увеличению налоговых щитов, которые будут иметь, однако, неизменный риск, поскольку EBIT тоже растет с темпом g , так что для равенства итогов оценки фирмы методом ECF и прочими методами нужно отталкиваться от «финального» уровня долга D .

Таким образом, традиционная формула WACC не учитывает «финальный» уровень долга D = K D x D BOOK / ( K D - g ), поэтому корректный аналог для (2.12) выглядит так:

WACC _ K_FE + KD ⁽1- т D BOOK ) D .

(4.107)

^EV D ( D J V

Поскольку «финальный» размер долга D выше его начального учетного значения, расчет по формуле (4.107) дает более высокую величину WACC по сравнению с «классической» формулой (2.12), что снижает рыночную стоимость фирмы.

Именно по этой причине выражения (4.103) и (4.104) корректируются на g x V TS / V . «Классическая» формула (2.12) переоценивает V_TS , поскольку она предполагает, что фирма получает выгоды от налогового щита TS 1 = K D x D x _т начиная с первого года, в действительности реализуя в этот год налоговый щит TS 1 = K D x ( D BOOK )₀ x т , который меньше K D x d x т , поскольку ( D BOOK )₀<  D . В реальности фирме требуется время, чтобы достичь этого «финального» уровня долга (строго говоря, «вечность»). Таким образом, коэффициент g x V TS / V корректирует WACC , делая ее немного выше.

Заметим, что в случае g > 0 рыночные элементы D и V_U растут с одинаковым темпом (поскольку EBIT и налоговые щиты растут с одним темпом), так что стоимость долга K_D , определяемая согласно (4.12), остается постоянной. Таким образом, в рамках этой модели можно рассматривать WACC для случая g > 0, а при моделировании переменной K_D каким-либо другим способом этого сделать нельзя.

Подведем итог этому разделу:

• •    для простой бесконечной модели без роста ( g = 0) формулы (4.90) и (4.91) дают WACC , эквивалентную классической формуле (2.12);

• •    для простой бесконечной модели с ростом ( g > 0) формула (2.12) недооценивает WACC , и только выражения (4.103) и (4.104) дают корректную оценку WACC на основе аксиомы о равенстве результатов оценки фирмы методами WACC и APV ;

• •    в общем случае, предполагающем стохастическое изменение EBIT и левереджа, WACC неприменима.

Иллюстрации и примеры

Графические иллюстрации поведения ставок дисконтирования и рыночных элементов баланса приведены на странницах 99–104 оригинальной работы. Рассмотрены три случая для маржинального фактора кредитного риска: n = 1, n = 2 и переменный: n = 1 + 2 x (d / VU). Все графики основаны на результатах решения полученных выражений для ставок дис- контирования и рыночных элементов баланса.

Численные примеры оценки рыночных элементов баланса и совокупной стоимости фирмы приведены на странницах 105–118 оригинальной работы. Рассмотрены три случая эволюции фирмы:

• •    бесконечная модель без роста при n = 1 + 2 х ( d / V U );

• •    бесконечная модель с постоянным ростом при n = 2;

• •    случай с полностью стохастическим поведением EBIT и структуры капитала при n = 1.

Внимательный читатель обнаружит в третьем примере некритическую ошибку при выборе K_TS , что, впрочем, ничуть не уменьшает ценность примера.