Оценка готовности студентов 1-2-х курсов - будущих учителей математики к освоению профильных дисциплин в вузе

Постановка проблемы. На протяжении последних лет наблюдается снижение качества математической подготовки выпускников общеобразовательных школ, несмотря на результаты Единого государственного экзамена (ЕГЭ) по математике (профильный уровень). Большинство первокурсников со средними и достаточно высокими баллами ЕГЭ имеют пробелы в знаниях школьного курса математики, допускают ошибки в ходе решения математических задач базового уровня сложности, вследствие этого испытывают трудности при освоении математических и естественнонаучных дисциплин на уровне среднего и высшего профессионального образования.

Цель статьи - провести анализ уровня предметной подготовки студентов младших курсов института математики, физики и информатики

Красноярского государственного педагогического университета им. В.П. Астафьева к освоению профильных дисциплин в вузе.

Обзор научной литературы по проблеме. В современных зарубежных исследованиях анализируется математическая подготовка обучающихся школ, выявляется влияние различных условий на качество обучения в разных странах [Bernardo, 2021; Gokce, Guner, 2021; Kang, Cogan, 2022; Lever, Diaz, 2020; Salas-Velasco, 2020; Tasci, Titrek, 2020]. Л.П. Квашко сравнивая содержание математической подготовки в России и Китае, делает вывод, что содержание, уровень сложности и терминология во многом идентичны [Квашко, 2022].

А.С. Котюргина, Е.И. Федорова, В.Б. Николаев, Ю.Б. Никитин, проведя анализ содержания ЕГЭ по математике за 15 лет, отмечают, что «пока ЕГЭ остается единственной безальтернативной формой аттестации выпускников школ и главным вступительным испытанием в вузы, неизбежны искажения результатов обучения и негативные явления в образовательной среде» [Котюргина и др., 2020, с. 31]. Б.К. Дураков, О.В. Кравцова, В.Р. Майер, Н.Д. Подуфалов, Д.В. Семенова, проведя тестирование остаточных предметных знаний первокурсников по всем разделам школьного курса математики, сделали вывод о достаточно быстром уровне их снижения [Дураков и др., 2022, с. 66]. Л.Б. Рей-хельгауз также констатирует проблему неустойчивости результатов математического образования [Рейхельгауз, 2019]. По мнению Е.А. Швед, Л.А. Болотюк и В.А. Болотюка, у студентов с достаточно высоким результатом ЕГЭ отсутствуют базовые знания по математике. «Умения, не подкрепленные теоретической базой, теряются очень быстро и не могут применяться даже при незначительном изменении формулировки задачи» [Швед, Болотюк Л.А., Болотюк В.А., 2022, с. 19].

Р.М. Чудинский провел исследование особенностей воздействия контекстных данных студентов на уровень их знаний на основе КИМ ЕГЭ [Чудинский, 2022]. Т.А. Чебунькина, С.Ф. Катер-жина, Ю.А. Собашко считают, что в начале обучения первокурсников необходимо проводить входную диагностику, чтобы получить объективную оценку их знаний и определить дальнейшую программу обучения [Чебунькина, Катер-жина, Собашко, 2019].

В школьном образовании отсутствуют механизмы своевременного обновления содержания математического образования [Сикорская, Джукашев, Крючкова, 2020, с. 65]. Содержание математического образования должно быть представлено не только в логике современной математики, но и в логике будущей профессиональной деятельности выпускника [Биджи-ев, 2019]. Основу математической культуры составляют базовые фундаментальные математические знания, понимание основных математических методов. Для обучающихся, нацеленных на продолжение математического образования в вузе, требуется более глубокое изучение понятий и методов математики. Математическая подготовка обеспечивает овладение общекультурной когнитивной стратегией в решении профессиональных задач, а математика указывает эти направления и обеспечивает студентов научной установкой [Тестов, Перминов, 2021, с. 27].

Для обеспечения преемственности «школа – вуз» необходима согласованность в содержании образования и технологиях обучения [Одоевцева, Эйрих, Кириллова, 2022]. В.И. Сафонов, О.А. Бакаева, Е.А. Тагаева исследуют проблему реализации преемственности математического образования с помощью информационных технологий, позволяющих проводить исследование математических объектов [Сафонов, Бакаева, Тагаева, 2019]. О.К. Подлипский предлагает трансформировать математическую подготовку школьников с помощью цифровизации и практической ориентации для получения знаний, востребованных на протяжении жизни и в будущей профессии [Подлипский, 2020]. Одним из важных средств практической подготовки студентов является применение информационных технологий и инновационных методов в образовательном процессе, направленных на усиление практической подготовки [Kuzmina, Protas, Fartushok et al., 2020]. Обеспечить преемственность можно путем проектирования

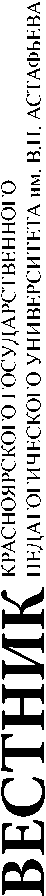
такой технологии обучения, которая предусматривала бы дифференцированный подход на индивидуальном уровне [Кулакова, Рейханова, Букина, 2019, с. 164].

Современный этап развития математического образования обусловлен активным поиском результативных технологий обучения математике в школе и в вузе. Так, например, С.Н. Дво-ряткина и О.А. Табинова в своих работах представили модели для организации процесса обучения математике как в школе, так и в вузе для достижения высоких результатов [Dvoryatkina, 2022; Табинова, 2019].

Важнейшими условиями реализации непрерывного, в частности математического, образования является самомотивация человека к образованию и его «умение учиться» [Брейтигам, 2020, с. 22]. Формирование системы непрерывного образования в современных условиях позволяет получить гарантию высокого качества обучения при ориентации на массовое образование [Nikiforov, Avdonina, Dikova et al., 2020].

Методология и методы исследования . Методологическую основу исследования составили: системно-деятельностный подход как методологическая основа федерального государственного образовательного стандарта основного среднего образования; компетентностный подход как методологическая основа федерального государственного образовательного стандарта высшего образования по направлению подготовки Педагогическое образование; профессиональный стандарт «Педагог (педагогическая деятельность в сфере дошкольного, начального общего, основного общего, среднего общего образования. Модуль «Предметное обучение. Математика»). В исследовании использованы методы анализа специальной литературы и нормативных документов, методы статистической обработки данных.

Результаты исследования. Ежегодно в начале учебного года в институте математики, физики и информатики Красноярского государственного педагогического университета им. В.П. Астафьева проводится входное тестирование по элементарной математике для про- верки остаточных знаний у первокурсников, поступивших на направление подготовки 44.03.05 Педагогическое образование, направленность (профиль) образовательной программы «Математика и информатика».

В исследовании принимали участие: в 2021 г. 40 первокурсников; в 2022 г. 46 обучающихся 1-го курса и 40 обучающихся 2-го курса (первокурсники 2021 г.).

Средний балл по результатам ЕГЭ (математика, профильный уровень) у первокурсников 2021 г. составил 61,9 (самый высокий и низкий баллы 86 и 39 соответственно), у первокурсников 2022 г. – 60,9 (самый высокий и низкий баллы 80 и 34 соответственно).

Контрольно-измерительный материал входного тестирования состоял из 10 заданий, которые проверяли усвоение на базовом уровне школьного курса математики.

Задание 1, в котором необходимо было определить сумму корней уравнения (2х2 + 3х)2 -?(2х2 + Зх)=-10, верно выполнили: 65 % первокурсников 2022 г., 14 % первокурсников 2021 г., 88 % второкурсников 2022 г. Не все тестируемые смогли правильно определить метод решения, который заключался во ведении новой переменной. Некоторые правильно определили метод решения, но забыли осуществить обратную замену. Некоторые допускали вычислительные ошибки в ходе решения квадратных уравнений.

Задание 2, в котором нужно было решить дробно-рациональное неравенство вида (х-2)(х + 3)2

-———— > о, верно выполнили: 15 % перво-х + 5

курсников 2022 г., 39 % первокурсников 2021 г., 57 % второкурсников 2022 г. Большинство студентов продемонстрировали низкий уровень владения методом интервалов. Ошибки при определении знаков постоянства алгебраической дроби. Большинство полученных ответов отличались от верного невключением точки .

Задание 3 состояло в решении неравенства с модулем |-х-2,5|<2. Верно выполнили это задание 30 % первокурсников 2022 г., 29 % первокурсников 2021 г., 64 % второкурсников 2022 г.

Большая часть ошибок заключалась в неправильном и некорректном оформлении решения неравенства.

В задании 4 требо вал ось найти значение выражения . Процент верно выполнивших данное задание составил: первокурсников 2022 г. - 24 %, первокурсников 2021 г. – 32 %, второкурсников 2022 г. – 76 %. Основная трудность задания состояла в том, чтобы представить подкоренное выражение в виде полного квадрата суммы или разности. Многие забывали про модуль при извлечении квадратного корня из квадрата.

Задание 5, в котором необходимо было вычислить произведение всех корней иррационального уравнения л!х + 5 = х-1, верно выполнили: 20 % первокурсников 2022 г., 18 % первокурсников 2021 г., 79 % второкурсников 2022 г. В ходе решения иррационального уравнения многие из студентов не следили за равносильностью преобразований, в результате чего в ответ включили посторонний корень.

Самый низкий результат был получен в ходе выполнения задания 6. Верно выполнили это задание: 0 % первокурсников 2022 г., 0 % первокурсников 2021 г., 60 % второкурсников 2022 г. В задании 6 требовалось решить иррациональное неравенство вида Jx + 7 >х-1. Большинство первокурсников не владеют алгоритмами решения и правилами равносильных преобразований иррациональных неравенств.

Задание 7, в котором необходимо было найти значение выражения , верно выполнили: 41 % первокурсников 2022 г., 25 % первокурсников 2021 г., 83 % второкурсников 2022 г. Ошибка заключалась в неправильном применении свойств степеней и свойств логарифма числа.

Задание 8, в котором необходимо было решить логарифмическое неравенство вида

, верно выполнили: 13 % перво- курсников 2022 г., 21 % первокурсников 2021 г., 38 % второкурсников 2022 г. Не все тестируемые учли область определения неравенства и то, что логарифмическая функция убывающая.

В задании 9 требовалось найти сумму кор-1 -3 1

ней уравнения . Процент верно выполнивших данное задание составил: первокурсников 2022 г. – 13 %, первокурсников 2021 г. – 14 %, второкурсников 2022 г. – 40 %. Основная трудность решения показательно-степенного уравнения заключалась в правильном применении метода логарифмирования, с помощью которого уравнение сводится к квадратному логарифмическому уравнению. Многие забывали про область определения уравнения.

Задание 10 заключалось в решении задачи на сложные проценты. Верно выполнили это задание: 46 % первокурсников 2022 г., 46 % первокурсников 2021 г., 45 % второкурсников 2022 г. Ошибки в решении задания 10 обусловлены невнимательным чтением условия, непониманием понятий «процент» и «сложный процент», неумением выполнять процентные вычисления.

Таким образом, содержание контрольноизмерительных материалов входного тестирования охватывает все основные темы школьного курса алгебры. Заметим, что все задания теста имеют базовый уровень сложности.

Результаты исследования показали, что большинство первокурсников имеют крайне низкий уровень освоения школьной программы по алгебре. На диаграмме (рис. 1) представлены результаты выполнения отдельных заданий входного теста.

В ходе исследования были сформированы две выборки ( X – результаты ЕГЭ по профильной математике, Y – баллы за входное тестирование) и проведен корреляционный анализ. Подробно результаты корреляционного анализа для первокурсников 2021 г. представлены в работе [Кейв, Кобычева, Шашкина, 2021]. Для первокурсников 2022 г. величина коэффициента корреляции составила 0,402, что указывает на прямую умеренную связь между признаками. t-критерий Стьюдента равен 2,812, что больше критического значения 2,021 (число степеней свободы - 41), зависимость признаков статистически значима. Коэффициент ранговой корреляции Спирмена 0,415 указывает на умеренную прямую связь между

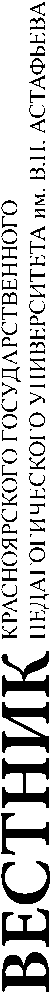
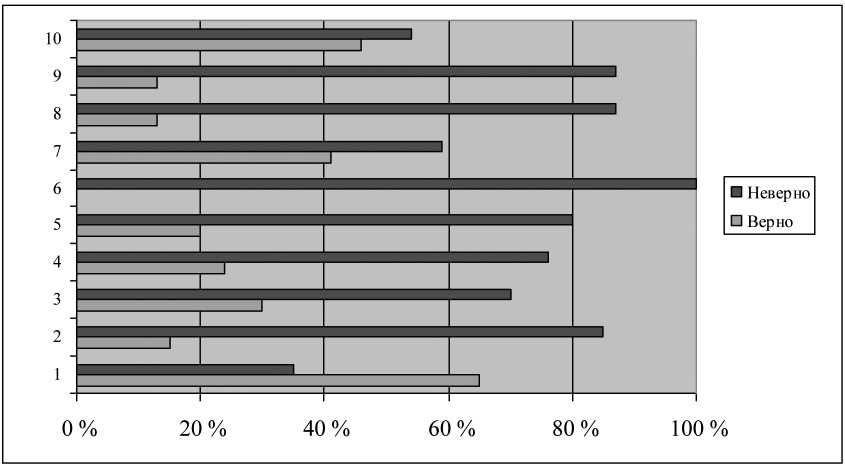
Рис. 1. Распределение ответов студентов по типу правильно решенных заданий теста, %

Fig. 1. Distribution of students’ answers by type of correctly solved test assignments, %

признаками X и Y , а критическое значение критерия Спирмена (число степеней свободы – 41) равно 0,301, что говорит о статистически значимой зависимости между признаками. Недостаточно тесная связь между величинами обусловлена различным набором заданий ЕГЭ и входного теста, что говорит о формальности математических знаний у большинства первокурсников и больших пробелах в математической подготовке. Кроме того, проведенное исследование заставляет усомниться в объективности оценки предметных результатов освоения программы по математике в формате ЕГЭ.

Заключение. Безусловно, уровень предметной подготовки у первокурсников различный, у большинства из них имеются пробелы в школьном курсе математики, что не может в дальнейшем не сказаться на успешности освоения математических курсов в вузе. Позитивную роль в выравнивании предметной подготовки и повышении уровня владения базовыми математическими знаниями школьного курса математики может сыграть вводный курс математики или практикум по решению школьных математических задач. Данный тезис обосновывают полученные результаты исследования (рис. 2).

Рис. 2. Диаграмма сравнения результатов входного тестирования обучающихся в 2021 и 2022 гг.

Fig. 2. Diagram comparing the results of entrance testing of students in 2021 and 2022

Первокурсники 2021 г. на протяжении первого года обучения осваивали дисциплину «Школьный практикум по дисциплинам (математика)». Если сравнить их результаты входного теста в 2021 г. с результатами, полученными в ходе входного тестирования в 2022 г., то можно зафиксировать положительную динамику. Большинство второкурсников после изучения школьного практикума смогли правильно выполнить практически все подобные задания, которые год назад вызывали у них затруднения.

Представленный в статье анализ уровня предметной подготовки студентов младших курсов института математики, физики и информатики Красноярского государственного педагогического университета им. В.П. Астафьева свидетельствует о недостаточной готовности первокурсников к освоению профильных дисциплин в вузе. Уровень качества школьного математического образования несомненно влияет на процесс дальнейшего освоения курса математики в вузе, поэтому особое внимание необходимо уделить входной диагностике предметных знаний первокурсников и включить в учебный план образовательной программы вводный курс по математике.