Оценка информационных параметров сигнала на фоне аддитивно-мультипликативных помех с произвольным распределением

Вопросы измерения информационных параметров полезных сигналов в информационно-измерительных и управляющих система, системах связи, телеметрии, радиолокации и радионавигации весьма подробно рассмотрены в [1; 2] и др. В большинстве работ считалось, что на полезный сигнал воздействует только аддитивная помеха, описывающаяся, как правило, гауссовской плотностью распределения вероятности (ПРВ). Однако, как показывают исследования [3–5], принимаемый сигнал подвержен воздействию не только со стороны аддитивных, но и мультипликативных помех, имеющих ярко выраженный негауссовский характер. Для радиолокации, радионавигации и телеметрии представляет значительный интерес получить оптимальную оценку параметров обрабатываемых сигналов в условиях одновременного воздействия аддитивных и мультипликативной помех с произвольной плотностью распределения вероятности.

Рассмотрим случай, когда элемент yh наблюдаемой последовательности {yh, h = 1, 2, ..., H} описывается соотношением yh = nhs (^h) + nh; h = 1, 2, •••, H, (1)

где s ( X h ) — сигнал известной формы, несущий информацию о передаваемом сообщении { x h } , а метод кодировки сообщения в сигнале известен.

Последовательности { n h } , { n h } описывают мультипликативную и аддитивную помехи соответственно; { х h } — непрерывнозначная марковская последовательность.

Считаем, что последовательности { х h } , { n h } , { n h } заданы своими условными, в общем случае, негауссовскими ПРВ перехода W X ( X h |X h - 1 ) , ^W n ( n h |n h - 1 ) , W n ( n h n h - 1 ) .

Будем считать, что логарифм функции правдоподобия B_l существует и может быть записан как относительно мультипликативной

B n = ln W n ( [ y h ^{- n} h ]/ ^s ( ^X h )| [ y h - 1 ^- n h - 1 ]/

/ s (X h)) s 1 (X h )|, так и относительно аддитивной

Bn = ln Wn (Уп - nns (Xh ) yh-1 -- nh-1s (Xh-1)), составляющей помехи. Например, при первом способе описания ЛФП алгоритм обработки содержит взаимно зависимые каналы обработки информационной последовательности Xh и аддитивной составляющей помехи nh. При втором способе задания ЛФП оцениваются X h и n h соответственно. Получить эти алгоритмы можно известными методами [6]. В дальнейшем рассмотрим второй случай.

Записав рекуррентные соотношения для апостериорной ПРВ, разложив его в ряд Тейлора ооT около вектора предварительных оценок Xh, nh ) и ограничившись линейными и квадратичными членами в гауссовском приближении, получим рекуррентные уравнения, описывающие ква-зиоптимальный алгоритм оценки в условиях одновременного воздействия коррелированных мультипликативных и аддитивных негауссовских помех, с независимыми значениями:

где Gij.h – алгебраическое дополнение элемента матрицы gj ; Ai1 — определитель матрицы gij ;

[rx'      i ',KJFrX",x'

gX.h     [BX.h + BX.h J + {[BX.h.h-1BX.h-1J x x [Bn.h-1.h-1 + onn.h-1J +

⁺ [ B X . h . h - 1 B n . h - 1 ^o nX . h - 1 J } ^A 2 ^1;

^g n . h     [ B n . h ⁺ B n . h J ⁺

⁺ { [ B n h . h - 1 B X h -1 ^о хП . h - 1 J +

⁺ [ B n h . h —1 B n h - 1 J[ B X h - 1. h - 1 + ^o xX . h - 1 J } ^A 2 ^1;

^g XX . h = [ B X .h . h ⁺ B{ . h . h J ^-

• ^- { B X . h . h - 1 J [ B^h - 1. h - 1 ^{+ O} nn h - 1 Jl^A 2 ^1;

[ Rnl gnn.h   I BX.h.h + Bn.h.h

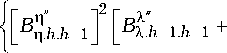
~-2       I ^-1-

^O XX . h - 1 I । ^A 2 ;

_D l"         foX "     on "        -2     ) A- 1.

• ^g Xn . h B Xn . h . h { B X . h . h - 1 B n . h . h - 1 ^o nX . h - 1 } ^A 2 ;

• ^g nX . h = B j X . h . h ^- { B n . h . h - 1 B X . h . h - 1 ^o Xn . h - 1 } ^A 2 ;

• ^A 2 = [ B ^X h - 1. h - 1 ^{+ o} xX . h - 1 J ^x

• ^x [ B n . h - 1. h - 1 ^{+ o} nn . h - 1 J ^- [^o Xn . h - 1 ^o nX . h - 1 J , X' n       X"      n''

BX.h, Bn.h, BX.h, Bn.h - первые и вторые произ— водные от логарифма ПРВ перехода информационной последовательности {X h} и мульти пликативной помехи {nh } соответственно; BXh, Bn h — производные ЛФП по соответствующему

.

оо параметру; X h, nh — предварительные оценки информационного процесса и мультипликативной составляющей помехи, найденные одним из известных способов.

Уравнения (2) и (3) описывают, соответственно, рекуррентные алгоритмы работы каналов формирования оценок информационной составляющей X h и мультипликативной помехи n h ■

Уравнения (4) представляют матрицу апостериорных нестационарных дисперсий и описывают структуру каналов формирования коэффициентов усиления в уравнениях для оценок (2), (3).

Математический анализ полученных алгоритмов демодуляции, в общем случае, наталкива- ется на значительные математические трудности и может быть выполнен численными методами. Поэтому, воспользовавшись подходом, изложенным в [7], рассмотрим более простые случаи быстрых и медленных изменений мультипликативной помехи.

Считаем, что мультипликативная помеха {nh} описывается неотрицательной функцией с нуле- вым средним mn, т. е.

n h = m n ( 1 ⁺ П о h ) = m n ⁺n h ,                   ⁽⁵⁾

*   -1. ?

где n o h = n h m n ; n h = ( n h ^- m n ) ^- центрированное значение n _h .

Тогда, уравнение (1) представим в виде yh = sh (Xh)(nh + mn) + nh.

В случае быстрых изменений n h спектр мультипликативной помехи F_mn считается гораздо шире спектра информационного процесса (сообщения) F , так что F » Е„ .

s            mn s

В этом случае можно сделать приближенную замену (nh + mn) средним значением mn (1 + ^2 ), где ^2 = оП /mn — квадрат коэффициента вариа- ции случайного процесса случайного процесса {nh}.

{ ⁿ h } , ^o n

–

дисперсия

{ ^X h } ^и { n h } некорре-

Положим, что процессы

лированы, то есть O xn = 0. В этом случае уравнения (2), (3) могут рассматриваться независимо друг от друга.

В качестве предварительной оценки принимаем экстраполированную Xh = Xe h, определяемую из соотношения d ln Wx(Xh ^h-1) = 0 дх h

Опуская для простоты, при дальнейшем рас-

смотрении, уравнения для оценки мультипликативной составляющей n h (3), ограничимся рассмотрением лишь структуры канала оценки информационной последовательности и канала (4).

уравнения (2), (4)

л - 1

= XX . h - 1             ⁽⁷⁾

д'           ’ ^.

' X. h - 1. h - 1

Заметим, что здесь волнистая линия означает усреднение по времени, прямая – усреднение по множеству.

В результате алгоритм обработки (6), (7) при-

нимает вид

апостериорной дисперсии (2),

С учетом примут вид

ZX           ZX

выше сказанного

^X h = ^X e . h + ^Q XX . h B X . h ;

~ 2  . -

= XX . h

X ' l ''

B X . h . h + B X . h . h ^-

( B x'h . h - 1 ) 2

¹ + = XX . h - 1

Считаем, что измеряемая информационная

последовательность

марковской с ПРВ перехода

{ x h } является гауссовской

W x ( X h |x h - 1 ) =

__________1_________ j -(Xh - rXXh-1) "[2^(1 - rX)f “p 1 2=X(1 - r) J’ где Qx.h = =X.h-1 = =X, а ПРВ аддитивной помехи описывается одномерной бимодальной ПРВ

W n ( n h ) = A ^exP { Pn h ^{2 -} gn h 4 } >               ⁽⁸⁾

где А – коэффициент нормировки; p и g – параметры распределения.

В этом случае компоненты, входящие в (6), (7)

примут вид

B X hh = [= X ( 1 - r 2 ) ] " * ;

"                        X"

B X . h . h - 1 " ^- r _x B X . h . h ;

B X . h - 1. h - 1 " ^{- r} X B X . h . h ^;

B L = ^- ( n h ⁺ m n ) s h ( ^x h ) ^[ 2 pn h ^{- 12} gn h ] ;

i *              ²

B X . h . h = ( n h ⁺ m n ) ^x

^x[ s h ( ^x h ) ] ^[ 2 pn h ^{- 12} gn h ] +

+ ( n h ⁺ m n ) s h ( ^x h ) ^[ 2 pn h ^{- 12} gn h ] .

Если измеритель будет работать в стационарном (установившемся) режиме, то, сделав ус-

реднение по времени и по множеству, вторая производная ЛФП будет определяться

i"

B -X. h . h

= ( n h + m h ) s h ( ^X h )

П ² = „''

I B n . h . h =

= U 2 c m n ( 1 + ^ ² ) [ p ^- 6 gm 2 n ] .

/X           /X

^X h = ^X e . h ⁺

/X

^{+ Q} XX . h

^[ s h ( ’^ h )( ⁿ h ⁺ m n

) ( ⁴ gn h ^{- 2} pn h ) ] ;

^ 2  , -

^Q XX . h

( = 2 ( 1 - r 2 ) + r ² ; Xx . h - 1 ) ^{- 1} +

расчетное значение стационарной относительной дисперсии оценки информационной последовательности при = Xx . h = ^Q xx . h - 1 = ^q2 в виде

£ . S

я! = X

( 1 - r X 2 ) ( 1 + P 2 g ( 1 + ^ 2 ) ) 2 r x ² P 2 g ( 1 + ^ 2 )

1 ₊       4 r x ² p g ( 1 +^ ² )

( 1 - r 2 ) ( 1 +p g ( 1 +^ ² ) ) ²

V v / \       ^ \         //

Анализ зависимости 5 ^ . _s = f ( p g ; r X ) для различных значений ^ ² при любой ПРВ аддитивной и мультипликативной помехи приводят к выводу, что значения 5 ^ _s зависят в общем случае от ОСП, вида ПРВ аддитивных и мультипликативных помех, определяющих B n hh и ^ 2 .

Нетрудно видеть, что при точно известной мультипликативной составляющей помехи эффективность нелинейной обработки возрастает с ростом величины ^ ². Если принять ^ ² = 0, то получаем формулу для относительной дисперсии оценки информационного параметра при воздействии только аддитивной негауссовской помехи.

Таким образом, учет быстрой мультипликативной составляющей помехи приводит к повышению качества обработки принимаемой реализации. Повышение эффективности соответствует увеличению ОСП в (1 + ^ ²) раз. Техническая реализация алгоритма, учитывающего быструю мультипликативную составляющую, значительно усложняется, однако выигрыш, который наблюдается от ее учета, может быть значителен.

Проанализируем влияние аддитивных помех на конечный результат.

Воспользовавшись известным [8] соотношением

^^^^^^в

■ M { d ² ln W n ( n )/д n ² } =

= M { ( d In W_n ( n )/d n ) 2 } , что соответствует равенству B n

помехи допустимость использования введенного и некоторых других приближений (например, регулярности) требует самостоятельного рассмотрения.

Обратимся к случаю медленных изменений

^— ( B n ) и бу-

дет иметь место, например, в случае ПРВ (8) при

Р = ( 8 m 2 n ) ^{— 1} { ( 16 gm 4 n ^{+ 2} ) ±

мультипликативных помех, имеющих место, когда F ^ F _s.

mn s

Для удобства преобразований представим ^ ^ в

*

виде (5) так, что ^ h = m n + П ^ . Тогда соотношение для приведенной погрешности примет вид

± { 256 g ² [ m 4 n

—

m 2 n

—

m 6 n

S2.m (n‘ ) =

( *    _—

^{1 —} r X ) ( 1 ⁺ Р g ( 1 ^{+ n m} п ) )

+ ⁶⁴ g [ m 4 n ^— 3 m 2 n ] + 4 } ⁰ " ⁵ } .

Используя коэффициент амплитудного подавления негауссовских помех [8]

^ц оа = I F ^c n = ( B n ) ^c n , где I_F ⁿ – количество информации по Фишеру

2 r¥ _g ( 1 + n * m ^{—— 1} ) 2

относительно ПРВ помехи; c n 2   22

мехи, и представив р g = р g ц _оа. виде

–

дисперсия по-

, перепишем (9) в

^ £ . S

2 «L P G ( 1 + 4 2 )

X

X

4 »«а P G ( 1 + 4 2 )

0.5

— 1

.

Здесь P g = c² U 2 _c m ^ u n² характеризует ОСП в случае гауссовской помехи.

Коэффициент амплитудного подавления аддитивных негауссовских помех с бимодальной ПРВ, рассматриваемого вида, будет определяться [9]

^ц оа = ^{4 c} n ^ p ^c n ^{— 4 pm} 4 n ^{+ 4 g m} 6 n J .

Как известно, в случае гауссовских аддитивных помех ц Оа = 1. При негауссовских помехах ц , _а >  1 и погрешность измерителя дополнительно уменьшается за счет амплитудного подавления аддитивных негауссовских помех.

Таким образом, найденное соотношение позволяет проследить влияние на величину нормированной апостериорной погрешности не только мультипликативной, но и аддитивной негауссовской помехи.

Необходимо обратить внимание, что для каждого конкретного вида негауссовской ПРВ

(

1 +

v

⁴ r xp g ( 1 +n * m п ¹ )

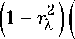
( * — 1 1 + n m п

0.5

2*

При этом 5_{е S} ( п )

*

ной величины п .

является функцией случай-

Заключение

Таким образом, представленные зависимости и проведенные расчеты показали, что при известной априорной ПРВ мультипликативной помехи точность демодуляции в случае медленных флюктуаций может быть значительно ниже, чем в случае быстрых флюктуаций. Причем, при точно известной мультипликативной составляющей помехи эффективность нелинейной обработки возрастает с ростом величины 4 2 .