Оценка ионосферной и тропосферной задержки сигнала СРНС при использовании одночастотного навигационного приемника

Применение фильтров калмановского типа (ФКТ) для оценки ионосферной и тропосферной задержки сигнала спутниковых радионавигационных систем (СРНС) наряду с оценкой координат и вектора скорости подвижного объекта, использующих измерения одночастотного навигационного приемника, является весьма актуальной задачей. Так как ионосферная и тропосферная задержки являются малоинформативными параметрами, то для их удовлетворительной оценки требуется проведение измерений сигналов как можно большего количества видимых спутников. В связи с этим необходимо использовать совмещённый навигационный приемник GPS+ГЛОНАСС. Приведем уравнения ФКТ [4].

Пусть x i / k означает оценку вектора x i , полученную на основании измерений, проведенных до момента времени k , а i обозначает дискретный момент времени, в который производятся измерения. Пусть P i / k обозначает матрицу ковариаций ошибок, связанную с оценкой x i / k .

Введем следующие вектора и матрицы:

^f ( x i/i ) = ^xi / i ;

A ( ^$"^-% I

^x = x i / i .

Тогда уравнение экстраполяции вектора состояния будет иметь вид x . ₊v i = x i / i + f ( x i / i ) -A t + A ( x i / i ) • f ( x i / i ) -A t ² /2 + Z i ;

E {Zi } = 0; E {ZiZTT } = Qi 8 *; 8 ik ={ 1, i = k,

[0, i Ф k где At - интервал дискретизации; Zi — вектор шума модели движения; E - оператор математического ожидания; Qi – матрица интенсивности шума модели.

Если в качестве измеряемого ввести вектор z _i , то связь оцениваемых и измеряемых параметров можно записать в виде z i = h i ( x i / i ) + s i . Здесь h i - вектор показывающий аналитическую зависимость измеряемых параметров от оцениваемых, s _i - вектор шума измерений.

Предполагаем, что E { s i s T } = N i 8 ik и E { s i } = 0, N i - матрица интенсивности шума измерений.

Уравнение коррекции вектора состояния xi+1/i+1 = xi+1/i+ Wi+1 [ zi+1 - h (xi+1/i)],                                                                       (2)

где W i _{+ 1} - матрица коэффициентов усиления фильтра, полученная как

W + 1 = P i + 1/ i ^H i + 1 ⁽ H i + 1 P i + 1/ iH i + 1 ⁺ N i + 1 ) ;                                                                ⁽³⁾

н = d h i

H i ^{+ 1}     5 x x = x i ^{+ 1/} i '

Определим переходную матрицу Ф _i , определяющую динамику оцениваемого движения, следующим образом:

Фi = I + A(X/i )-At,(4)

здесь I – единичная матрица.

Уравнение экстраполяции матрицы ковариаций

Pi+1/i = Ф iP / i Ф T + Qi.(5)

Уравнение коррекции матрицы ковариаций

Pi+1/i+1 =(I — W+1 Hi+1) Pi+1/i.(6)

На основании приведенных уравнений экстраполяции и коррекции получаем блок-схему

ФКТ, использующего информацию от навигационного приемника, которая представлена на рис. 1.

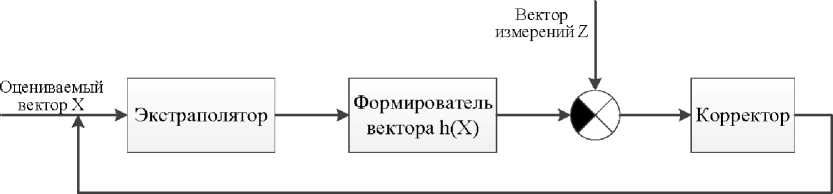
Рис. 1. Блок-схема ФКТ

Экстраполятор включает в себя уравнение экстраполяции вектора состояния и матрицы ковариации. Корректор включает в себя уравнение коррекции вектора состояния, уравнение коррекции матрицы ковариации.

Для предотвращения расходимости ФКТ введен адаптивный элемент в виде пересчета в каждый момент времени i матрицы Q_i :

Q i + 1 = Q min + 0, 1Q i + 0,7 diag { W + 1 [ Z + 1 — h ( X +1/ i ) ] } T { W + 1 [ Z i -+ 1 — h ( X +1/ i ) ] } •                    (7)

Коэффициенты 0,1 и 0,7 в приведенном выражении подобраны экспериментальным путем.

В работе рассмотрены стандартные модели ионосферной и тропосферной составляющих задержки навигационного сигнала для объекта, имеющего навигационные приемники и движущегося по поверхности Земли. Для описания задержки сигнала в ионосфере используется однослойная модель ионосферы [5], где предполагается, что все электроны сосредоточены в тонком слое, расположенном на некоторой высоте h над поверхностью Земли. Так величины фазового и соответственно группового ухода ПД, соответствующие ионосферной составляющей задержки для спутника, находящегося в зените относительно приемника, будут равны

40 3 г           40 3

I g =- I f = --2- J n e ( 5 ) dS = --2- Ns .                                                  (8)

f op S                f op

Здесь n_e ( S ) -зависимость концентрации электронов от высоты 5 ; N_s - концентрация электронов в слое ионосферы; f_op – некоторая единая для ГЛОНАСС и GPS частота, при которой будем определять величины фазового и соответственно группового ухода ПД.

I j ( t i ) - уход ПД для сигнала j -го спутника в ионосфере в момент времени t i определяется как [5]

I j (. t . ) = I g • fl f_j

•

1 -

H- j t A

где R3 - радиус Земли; h = 432,5 • 103 м - высота слоя ионосферы, где интегральная концентрация электронов в вертикальном столбе достигает 50 %; fj - несущая частота j-го спутника; n , (t.) — угол места j-го навигационного спутника относительно приемника.

Угол места навигационного приемника с достаточной для данной методики точностью можно получать из следующего выражения [3]

sin { n j ( t ) }

_________________(Xj( t.)-X (X (t.)_________________ V XT (o-X (i,) (X,( t.-)- X (t.)) T •( X, (у- X (y)

Здесь Xj = [х, (t.) y, (t.) Zj (t.)] - вектор координатj-го спутника; X = [x(t,) y(t.) z(t,)]T - координаты приемника в момент времени t .

Для описания тропосферного ухода ПД используется самая простая модель тропосферы [1], так как предполагается отсутствие информации о температуре, атмосферном давлении и пар- циальном давлении водяного пара:

Uj(t. ) =

U g

sin { n j ⁽ t . ) }

где U j ( t . ) - уход ПД для сигнала j -го спутника в тропосфере в момент времени t . , а U g - величина, близкая к 2,5, но постоянная на достаточно большом интервале времени.

Для уменьшения динамических ошибок в навигационном приемнике используют информацию об ускорениях объекта, на борту которого он установлен на этапе первичной обработки. Это позволяет оценивать в каждый момент времени t параметры навигационного приемника, включенные в оцениваемый вектор x./. = [5  У.   z.   А.   x.  y.   z.   А.   Ад,.   Ig,.   Ug,. ]T.                                      (12)

Здесь x , y , z – оценка координат приемника в момент времени t по измерениям вплоть до t ; А . - оценка ухода шкалы времени навигационного приемника относительно системного времени ГЛОНАСС в z -й момент времени, представленная в метрах по измерениям вплоть до t . ; А . -оценка скорости ухода шкалы времени навигационного приемника относительно системного времени ГЛОНАСС в -й момент времени, представленная в метрах по измерениям вплоть до t ; 5с. , у . , Z . - оценка скорости объекта в z -й момент времени по измерениям вплоть до t . ; А_а . -оценка ухода системного времени GPS относительно ГЛОНАСС, представленная в метрах по измерениям вплоть до t ; I_{g ,} – оценка группового ухода ПД вызванного ионосферой для спутника, находящегося в зените относительно приемника по измерениям вплоть до t ; U_{g ,} – оценка ухода ПД вызванного тропосферой для спутника, находящегося в зените относительно приемника по измерениям вплоть до t .

Все параметры вектора состояния непрерывно уточняются по мере поступления измерений по НКА ГЛОНАСС и GPS. Будем считать, что изменения скорости смещения шкал времени полагаются винеровскими процессами с малой скоростью дрейфа, которые характеризуется двухсторонней спектральной плотностью формирующего шума N ^ _v = 0,8 • 10 ^{- 22} Гц, что соответствует опорному генератору RTX5032A фирмы Rakon. Переход к моделям смещения часов в дискретном времени получается в результате интегрирования соответствующих непрерывных уравнений на интервале времени дискретизации. В нашем случае время дискретизации для вторичной обработки будет соответствовать интервалу выдачи ПД и ПС и равняться T = 0,1 с.

^A i = ^A i - 1 ^{+ T - A} i - 1 ⁺^ А , i - 1 ;

^А i = ^А i - 1 ^{+ i} A , i - I "

Таким образом, вектор формирующих шумов

£ i =

^ А , i

представляет из себя белый гауссов

шум с матрицей дисперсий [1]

T ³

T ²

M [^g ] = Q ^ = c ² - N

T ²

T

где c – скорость света в вакууме.

Рассмотрим первый вариант построения ФКТ. В нем в качестве измерений используются только измерения ПД и ПС в час тотном диапазоне L1. Приведем известные математические выражения для ПД [2]. Под ПД в навигационных приемниках понимается произведение скорости света c на псевдозадержку. Псевдозадержка в приемнике вычисляется как разность между показаниями часов приемника в момент приема и оценкой показаний часов спутника в момент излучения. В результате выражение для измеряемой в приемнике ПД по j -му спутнику имеет следующий вид:

D j X t i ) = R j X t i ) + c A T + c A j c ( j + T j -T ^j - T ip ) + i j , j = u ,               (16)

где t_i – момент прихода сигнала. Здесь также введены следующие обозначения: R _j – длина пути распространения сигнала от j -го спутника до приемника, равная

RjXt,) = (xj - *(t, ))2 + (j -У (t, ))2 + (2T - z(ti ))2 -                                      (17)

Здесь имеется в виду расстояние между точками, которые занимал j -й спутник в момент излучения и приемник в момент приема. Под моментом излучения понимают момент времени, который предшествует моменту приема на время распространения сигнала; A T - смещение часов приемника относительно системной шкалы времени (СШВ); A T^j - смещение часов j -го спутника относительно СШВ; T_tr^j_op – задержка кодового сигнала j-ого спутника в тропосфере; T_io^j_n – задержка кодового сигнала j -го спутника в ионосфере; т ^j - задержка кодового сигнала j -го спутника в радиочастотной части приемника; T_m^j_p – задержка кодового сигнала j -го спутника из-за многолучевых искажений; i j - шумовая составляющая измерения ПД j -го спутника приемником; J - общее число видимых спутников ГЛОНАСС + GPS.

Так как целью статьи является исследование тропосферных и ионосферных атмосферных задержек, примем, что многолучевые искажения, задержка кодового сигнала в радиочастотной части приемника, а также смещение часов спутников считаются скомпенсированными, а остаток – включенным в шумовую составляющую измерений. В этом случае запишем упрощенную математическую модель измерений ПД для ГЛОНАСС в виде

Dj X ti ) = Rj X tt) + c-A T + c • Trrop + c • Т0й +ij = Rj (tz ) + A( tj + Uj (tz) + Ij (tz) + ij .           (18)

Здесь

A = c-AT ;

U j X t i ) = c - T^rop ;

I j X t i ) = c - T on -

Упрощенная математическая модель измерений ПД для GPS записывается в виде

Dj X ti ) = Rj X ti) + c-A T + c - T^.op + c - TOn +ij = Rj X ti ) + A( ^ + Aa( ti) + Uj (ti) + Ij (tt ) + ij - (19)

Для получения ПС используются измерения псевдодоплеровских смещений Fj ( t^ ) несущей частоты, которые измеряются в приемнике по j -му спутнику в момент времени t_i , согласно [2], их выражения можно записать в следующем виде

R

F j ( t_; ) = -   - k -Е f i , mo - F ,                                                                 (20)

XJ где Rj – радиальная скорость приемника относительно j-го спутника в момент ti , определяе- мая как j ti')=—

—

xj — x (ti))+(y? — y (ti))(yj — y (ti ))+(T — z (ti))( zj

—

^Rj ( t i )

,

где X ^j - номинальная длина волны несущей j -го спутника; У = f njom / f_mo - постоянный коэффициент, равный отношению номинальной частоты f_n^j_om несущей j -го спутника к номинальной частоте f mo задающего генератора приемника; £ f i _mo - смещение частоты задающего генератора приемника относительно своего номинального значения в момент t i ; ^ F - ошибка измерения псевдодоплеровского смещения несущей частоты в приемнике.

Здесь предполагается, что ошибки псевдодоплеровских смещений из-за ионосферы и тропосферы малы и не учитываются.

Умножая левую и правую части выражения (3) на X j , получаем выражение для ПС приемника

Dj (ti ) = —XjFj (ti ) = Rj (ti ) + A(ti ) + Xj^F,

здесь ^a ( t i ) = ^{X j}k^j £ ^f , _mo .

С учетом приведенных уравнений ПД и ПС связаны с оцениваемым вектором следующими соотношениями:

– для ГЛОНАСС:

^D , ⁽ У ^r , ^+a . ⁺ sin { j t i ) } ⁺ 'ti

•

^fo ² p f j ²

•

1 —

R 3y Hⁿ j ⁽ t i ^)}

;

– для GPS:

^Dj ⁽ v) R j +Ms_m{n g (_лу I g,

•

f o ² p f j ²

•

1 —

R ²

Й «» K( У

^{+ a} a , i .

D j ( t i ) = R j +a i ;

cos {n j (t)} получаем из sin {n j (t)}, а sin {п?( ti )} = 7r/

s, =( у — Xi) Xi +(yj — y,) yi +(z™ — _-i) z;

r = 7x,2 + y2 + z2 ;

R j

= A

cn x_j

- xi)2 +(yc

—

^yi ^{) 2 +( z}c” ^{— z}i ^{)2 ;}

■     ( x Cn

Rj =

— Xi)(xcn — xi) + (yj — у, )(ycn — yi) + (zj — z, )(zcn — zi )

Rj где

Введем вектор измерений z _i в виде

z^i = D 1 ( t i )   D 2 ( t i ) .

- D j ( t i ) D ( t i ) D 2 ( t i )

• ^DJ ( t i )l T .

Тогда вектор h ( x i / i ) и матрицу H i можно записать:

a x

5 ^Dj .( j

a у .

dDj _(

^d z i

^s 2 =

^s 3 =

Hk (xi / i ) = cn

j h (X ) = [ D1

5 ^Dj ₌( x

D 2		Dj  D ) 1	D ) 2		T dj ] ;	;
■ a D 1 a x.	a D 1 а у.	a D 1 d z i	1	0	0	0	0	6 1	« 1	3 1
a d 2 a x.	a d 2 a y .	a d 2 d z i	1	0	0	0	0	O 2	a 2	З 2
d Dj a x.	d Dj a y .	d D j d z i	1	0	0	0	0	6 j	a j	3 j
a D ) 1	a D ) 1	a D ) 1	0	a D ) 1	a D ) 1	a D ) 1	1	0	0	0
a x.	a y .	d z i		a 5ci	a y.	d z .
a D ) 2	a D ) 2	a D ) 2	0	a D ) 2	a D ) 2	a D ) 2	1	0	0	0
a x.	a y .	d z i		a xc.	a y.	d z .
d D ) j	a D ) j	a D ) j	0	a D ) j	a D ) j	d D ) j	1	0	0	0
_ a x.	a y .	d z i		a xc.	a y.	d z .
— x i )	+ S 2 ^ H	+ s 3 S 11 ;

—

y < )

Rj

cn z j

—

zi

)

Rj

+ S 2 S 12

^{+ S} 3 ^S 12 ;

2 s 13

3 s 13 ,

^— I g , i

•

² op

f j ²

•

(1 — b 1² ) • b ₂ • sin

{ n j ⁽ t i ) } ,

b ₁

;

^{— U}g , i

^s11 =

^s12 =

^s13 =

x

cn

j

•

—

sin ² { n j ⁽ t i ) }

2 • X i

r • R j

ycjn

—

—

s ₁

r ²

• R

j

z

2 • yi

r • R j

cn

■j

—

2 • Z i

r • R j

—

—

s ₁

r ² • R

s ₁

;

•

j

r ² • R

,

. X* R j   ^r ( X

cn

j

—

x ) , _;

•

•

r

R j

I y i • R j   r ( y r

< _____________■!___2_________

zi

;

—

y i ) , ;

r

R j

;

• R ,    r ⁽

—

cn z j

—

zi

)L

r

R j

;

bi = V ¹ - ( b 2 ■ cos { n j ( ti ) } ) ² ;

b ₂ = -R³— ;

²   R 3 + h

9 j = 0 для сигналов системы ГЛОНАСС и 9 j = 1 для сигналов системы GPS;

^а j =

^fo ² p f j ²

■-------- b1

sin { n j ⁽ t i ) } ;

^d D j = ( x  ^- X i ) . 5 D j = ( y j ^- у, ) ; a D j = ( z" ^- z, ) ;

dXi       RJ ’ dyi        RJ ’ dZi       RJ ’ aD = (j - Xi) -   (x, - X,);

d x,      R j       R j     R j ;

a o j = ( y" - y , ) - У ( y" - y , ) . d у,      R j       R j     R j    ;

a c j = ( Z "n - Z i )   R j ( z -n - Z i )

d Z    R j R R "

Запишем Q _min как минимально возможную матрицу шума модели движения, удовлетворяющую разумным требованиям точности оцениваемых параметров.

	" 0,01	0	0	0	0	0	0	0	0	0	0
	0	0,01	0	0	0	0	0	0	0	0	0
	0	0	0,01	0	0	0	0	0	0	0	0
	0	0	0	q 11	0	0	0	q 12	0	0	0
	0	0	0	0	0,0001	0	0	0	0	0	0
Q min	0	0	0	0	0	0,0001	0	0	0	0	0
	0	0	0	0	0	0	0,0001	0	0	0	0
	0	0	0	q 21	0	0	0	q 22	0	0	0
	0	0	0	0	0	0	0	0	0,01	0	0
	0	0	0	0	0	0	0	0	0	0,01	0
	. 0	0	0	0	0	0	0	0	0	0	0,01

Здесь с учетом (15) получим

32 TT qii =° - ■ у, при qi2 = q 21 ^ - ■ у;

q 22 = ^ 2 ■ T , где ^ ² = 0,000007 (м/с)².

Матрица интенсивности шума измерений равна

oD      0 ...     0     0     0 ...     0" 0 oD2   ...      0     0      0 ...      0 0    0 • OD    0    0 .„    0 N = 00 ^  0 OD  0 ^  0 00 ^  00 oD2 ^  0 • • •               ...... • • •              • • •               ...... • • • _ 0    0 •    0    0    0 • oD J _ где oD - дисперсия измерений ПД, а O2D - дисперсия измерений ПС по j-му спутнику.

На рис. 2 и 3 представлены результаты эксперимента с описанным ФКТ. В эксперименте полагали, что СКО ПД оD = 6 м, СКО ПС оD = 0,064 м/с. При моделировании ионосферы вели- чина параметра Ig бралась равной 15 м, а при моделировании тропосферы Ug бралась равной 2,5 м. На протяжении всего времени наблюдения в пределах прямой видимости находилось не менее 12 спутников GPS+ ГЛОНАСС. Вектора координат и скоростей спутников системы GPS рассчитываются в системе координат WGS-84, поэтому для совместного использования измерений обеих систем необходимо их пересчитывать в систему координат ПЗ-90.02, соответствующую ГЛОНАСС [1]. На рис. 2 представлена ошибка оценки параметра Ig (series 2), а на рис. 3 ошибка оценки параметра Ug (series 2) в зависимости от времени наблюдения. Если считать, что оценка ФКТ параметров Ig и Ug с точностью 1 м приемлема для практики, то для этого требуется практически 500 с наблюдения.

Рассмотрим второй вариант построения ФКТ. В нем в качестве измерений используются измерения ПД и ПС, а также приращения псевдофаз в частотном диапазоне L1. Как указано в [5], применение псевдофазовых (ПФ) измерений может существенно увеличить точность определения задержек сигнала СРНС в ионосфере и тропосфере, что для случая применения ФКТ будет соответствовать уменьшению необходимого интервала наблюдений для получения приемлемых оценок.

Под ПФ в навигационных приемниках понимается разность между фазой гетеродина приемника на момент приема и фазой несущей частоты спутника на момент излучения [2]. В результате выраженная в циклах математическая модель ПФ, измеряемая в приемнике по j -му спутнику, имеет следующий вид:

R ( t i ). j j

V j (ti ) = fj (AT + A Tj) + —— + Ф0ф0-фh +ф Lp +Ф inn -ф m^p + M -sv j, (28) A где Aj = —— длина волны несущей j-го спутника; ф0 - начальная фаза приемника; фj - неоп-fj                                                                                                                              0

ределенная начальная фаза излучения j-го спутника; фh - фазовые аппаратурные искажения в j-м канале i-го приемника; фJtrnp - фазовые тропосферные искажения сигнала j-го спутника на входе приемника; фjon - фазовые ионосферные искажения сигнала j-го спутника на входе приемника; фJmp - фазовые искажения, вызванные многолучевостью сигнала j-го спутника на входе приемника; M j – неопределенное целое число, отображающее собой неоднозначность фазовых измерений в j-м канале приемника; ^V - шумовая составляющая измерения псевдофазы сигнала j-го спутника в приемнике.

С учетом включения многолучевых искажений в шумовую составляющую ПФ, а также компенсации аппаратурных искажений и ухода шкалы времени спутников, перепишем (28), умножив его на длину волны X j

G j ( t i ) = V j ( t i ) " X ^j = c T TT + R j ( t i ) + X ^j ( Ф о - ф 0 + Ф Lp ⁺ Ф ion - ?_v j ⁺ M ) =

= c ^ T^T + R j ( t i ) + ^{X j} ( ф о - Ф 0 - ^ j ⁺ M j ) + U j ( ti ) - I j ( ti ) .

Здесь учтен тот факт, что приращение времени фазового запаздывания, обусловленного ионосферой, имеет обратный знак по сравнению с приращением времени запаздывания огибающей сигнала [1]. Рассмотрим измеряемую величину

B j ( t i ) = D j ( t i ) -v j ( t J-X j ,                                                                        (30)

значение которой может быть получено из выражений (23) или (24) и (29)

B j ( t i ) = 2 I j ( t i ) + ^ ^j -X ^j ( Ф о -^- j M j ) .                                         (31)

Очевидно, что величина Bj (ti) неоднозначна из-за неопределенного целого числа Mj. Если же выбрать интервал времени, соответствующий ti - ti - к , такой, что на этом интервале величи- на M j постоянна, то можно воспользоваться следующей однозначной разностью измерений

B j ( t i ) — B j ( t i — _k ) = 2 • I j ( t i ) + ^ j ( t i ) + X j ^ ( t i ) — 2 • I j ( t i — к ) - £ j ( t i — к ) — X j ^ v j ( t i - к ) =

= ² • I gi

RR +Th «» Ш t i ) ) ]

1 -

R

³ cos

R 3 + h

• + ^ ^j ( t i ) -^ ^j ( t i - к ) +

+X ^j [₄( t i K j t i - к ) ] .

Здесь учтен тот факт, что величина I_{g , i} практически постоянна на интервалах времени ti - t i - к . В этом случае можно в ФКТ ввести дополнительные измерения

E j ( t i ) = ^Bj ( t i ) - ^Bj ( t i - к ) = ² • ^Ig,i\ - S I .

V b i      I

где

S =

RR + h =°s l ⁿ j ⁽ t i - к ) )

Интервал времени t i - t i - к выбирается из следующих соображений. Чем он больше, тем более информативно измерение E_j , но при этом увеличивается вероятность перескока фазы в канале слежения за фазой сигнала j -го спутника. Для работы по реальным сигналам необходим алгоритм, определяющий перескок фаз и отбрасывающий дополнительное измерение, соответствующее этому перескоку.

Введем вектор измерений z _i в виде

2 i = D i ( t i )   D 2 ( t i )   ^   D j ( t i )   D i ( t i )   I ) ₂ ( t i )   ^   I ) j ( t i ) E i ( t i ) E 2 ( t i ) - E l ( t i ) T .   (34)

Здесь L – количество дополнительных измерений с отсутствием перескоков фаз на заданном интервале.

Определим матрицу H i , а так же вектор h ( x i / i ) для второго варианта ФКТ с учетом дополнительных измерений.

тТ h (xi / i ) = [ D1  D2  •"  DJ  D1  D2  •”  DJ  Ei  E2  •”  EL ] ;

Г д Di

д D 1

д Di

1

0

0

0

0    9 1

a i    p i

s x

S yi

д zi

a d 2

д D 2

д D 2

1

0

0

0

0 9 2

a 2   P 2

д xi

д У i

д zi

д D j

д DJ

д DJ

1

0

0

0

0 9 J

...... a J  в J

д xi

д yi

д zi

• a D 1

д Di

д Di

0

д D ) 1

д D ) ,

д D ) 1

10

00

д xi

S y i

д zi

д x

д yi

дzi

a d 2

д D 2

д D 2

0

д D 2

д D ) 2

д D 2

10

00

H =

a x

S yi

д zi

д x

д yi

д zi

,

J a DJ

д DJ

д DJ

0

д DJ

д D ) J

д D ) J

10

00

a Xi

дyi

дzi

д Xi

д yi

дzi

д E

д Ei

д E

0

0

0

0

00

Yi      0 1

a Xi

д yi

дzi

д E 2

д E 2

д E 2

0

0

0

0

00

Y2     0 2

5 Xi

д yi

д zi

d el

д E l

д E l

0

0

0

0

00

Yl    0 L

d Xi

д У i

д zi

E = д xi

2 • S 2

SEl = 2 ^ дyt

SEl = 2 дzi

2

где

• s ii ;

S 2

s 12 ;

• S 2 • S

13 ; Y l =

--2 • Л b 1

Здесь l –

номера только тех спутников, у которых отсутствуют перескоки фаз на заданном

интервале.

>> 0 2 j         G j

На практике o D

. Тогда матрица интенсивности шума измерений будет равна

-

0

0

0

0 J.

0

° D i

0 J.

0 "

0

0

J.       0

0

0 J.

0

0

° D 2    -j

0

0

0

J ° D j

0

0 J.

0

0

0 j.

° D l

0

0

J.       0

О

2 D i

0 J.

0

0

0 J.

0

N =

0

0

J.       0

0 о

2 i ) 2   J

0

0

0 J.

0

,

0

0

J.       0

0

0 J.

° D j

0

0 J.

0

o i

0

J.       0

0

0 J.

0

2 o D i

0 J.

0

0

^ D 2

J.       0

0

0 J.

0

0

2 o D 2   j

0

... _ 0

0

J   ° D 1

0

0 J.

0

0

0 J.

2- ° D L \

^ D j

– дисперсия

измерений

ПД,

а ° D j

– дисперсия измерений ПС по j -му спутнику;

° к

– дисперсия дополнительных измерений EL

по L -му спутнику.

На рис. 2 и 3 представлены результаты эксперимента с описанным ФКТ. Условия этого эксперимента полностью соответствовали первому. Здесь полагали, что СКО ПД о D = 6 м, СКО ПС о d = 0,064 м/с, а СКО взвешенной величины ПФ о G. = 0,003 м. На рис. 2 представлена ошибка оценки параметра I_g (series 1), а на рис. 3 – ошибка оценки параметра U_g (series 1) в зависимости от времени наблюдения. Интервал времени t i - t i - k брался равным 90 с, так как считалось, что при хорошем соотношении сигнал/шум порядка 40 дБВт вероятность перескока фаз на этом интервале невысока. Если считать, что оценка ФКТ параметров I_g и U_g с точностью 1 м приемлема для практики, то для этого потребуется около 350 с наблюдения.

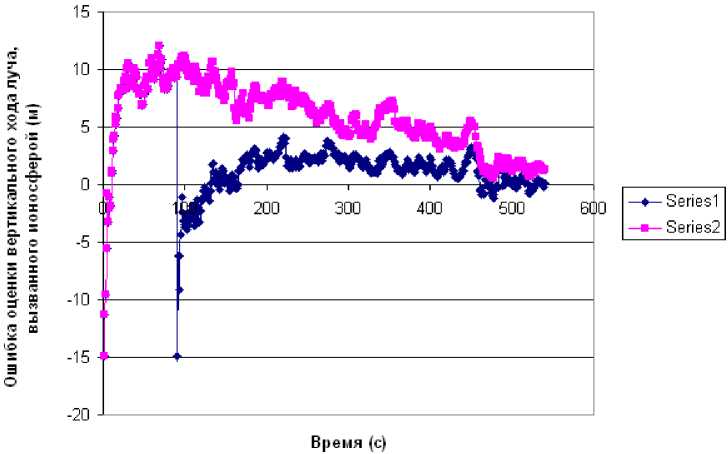
Рис. 2. Зависимость ошибки оценки ФКТ вертикального хода луча, вызванного ионосферой, от времени наблюдения

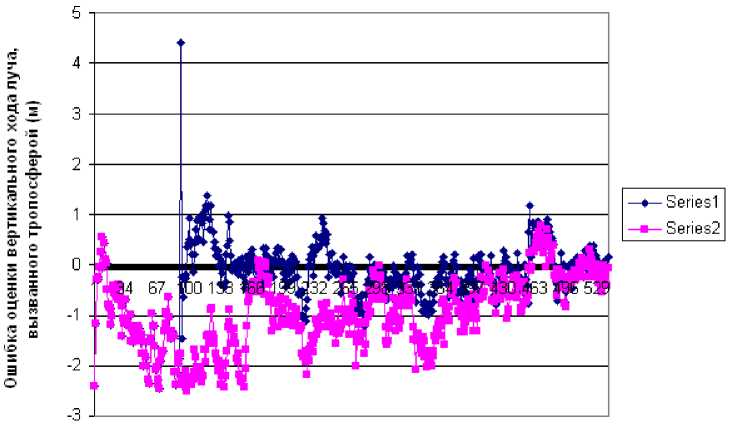
Время (с)

Рис. 3. Зависимость ошибки оценки ФКТ вертикального хода луча, вызванного тропосферой, от времени наблюдения

Рассмотрим третий вариант построения ФКТ, где используется непосредственное привлечение измерений ПФ. По сравнению со вторым вариантом, здесь в роли дополнительных измерений выступают неоднозначные измерения ПФ. Запишем (4) в виде

G j ( t i ) = C •A T + R j ( t i ) + K j + U j ( t i ) — I j ( t , ) — X j _S,

где K j = X j ( ф ₀ — ф 0 + M j ) .

С учетом введенных ранее обозначений для ПФ имеем следующие выражения: – для ГЛОНАСС:

Gj (ti ) = Rj + A i + Kj +

U g , i

sin { ⁿ j ⁽ t i ) }

—

I g , i

•

^fo ² p f j ²

•

1 —

R+н “^ t^

;

– для GPS:

G j ⁽ t i ) = R j + ^A i + K j +

U g , i

sin { n j ⁽ t i ) }

—

I g , i

•

f o ² p f j ²

•

1 —

Rt^h ^cos W "

^{+ a} a , i .

Значения K_j неизвестны, но считаются константами и требуют включения в оцениваемый вектор. Поэтому он будет выглядеть следующим образом:

Xi / i = [ X i   У ,   Z i  ^A i   x i   У i  zi   ^c i  ^A A , i   I g , i  ^Ug , i  ^K 1   ^K 2   -   ^KN ] T .             (38)

Здесь N – количество включенных в обработку ПФ измерений.

Введем вектор измерений z _i в виде

Z = D ( t i )   D 2 ( t i )   —   D j ( t i )   D ( t i )   D 2 ( t i )   —   D j ( t i ) G ( t i ) G 2 ( t i ) - G n ( t i )| ^T .  (39)

Определим матрицу H i , а также вектор h ( x i / i ) для ФКТ с учетом дополнительных измерений:

h ( X , /	) = [ D	D 2		D J	• D 1 D	2 —	• DJ	G 1	G 2		T GN ]	;
	г®, a x i	a D 1 а у ,	a D 1 a z i	1	0	0	0	0	6 1	a 1	3 1	0	0 j	0
	d D 2 a x i	a d 2 a y	a d 2 a z i	1	0	0	0	0	® 2	a 2	3 2	0	0 j	0
	d D j d x i	a D J a y ,	a D J a z i	1	0	0	0	0	6 J	a j	• • • 3 J	0	0 j	0
	• d D a x i	a i ) 1 a y	a i ) 1 a z i	0	a i ) 1 a xc,	a i ) 1 a y ,	a i ) 1 a z i	1	0	0	0	0	0 j	0
H i =	d D 2 a x i	a i ) 2 a y	a i ) 2 a z i	0	a i ) 2 a xc,	a i ) 2 a y ,	a i ) 2 a z i	1	0	0	0	0	0 j	0
	i a x i	a i ) J a y ,	a i ) J a z i	0	a i ) J a x c i	a i ) J s y ,	a i ) J a. zi-	1	0	0	• • • 0	0	0 j	0
	G a x i	a G 1 a y	a G 1 a z i	1	0	0	0	0	6 1	V 1	H 1	1	0 j	0
	a g 2 d x i	a g 2 a y	a g 2 a z i	1	0	0	0	0	6 2	v 2	^ 2	0	1 j	0
	' La x i	a G J а у ,	a G J a z i	1	0	0	0	0	6 N	V N	• • • H N	0	0	1

Здесь

д G j	( x T - x )
a x i	= Rj	+ S 2 S 11 + S 3	s 11 ;
д G j a y i	. ( y e - y i ) Rj	+ S 2 S 12 + S 3	s 12 ;
G дzi	( z? - z i ) = Rj	+ S 2 S 13 + S 3	s 13 ,
где 2 (1 op s 2 = I g , i • ,2 • fj		- b 2 ) • b 2 • sin { n j b 13		( ' i ) } ;
V j =	2 op 1 --— -- f j 2 b 1
^ j в j . Матрица интенсивности шума измерений имеет следующий вид
	° D 1      0	...       0	0	0 .	0	0	0 .	0 1
	0   ° D 2	...       0	0	0 .	0	0	0 .	0
	.    . 0     0	. °Dj	0	0 .	0	0	0 .	... 0
	0     0	...       0	° D	0 .	0	0	0 .	0
N =	,0 ,0	...       0	0	° D 2    •	0	0	0 .	. 0
	0 0	...       0	0	0 .	■  ° Dj	0	0 .	0
	0     0	...       0	0	0 .	0	° G,	0 .	0
	0     0	...       0	0	0 .	0	0	° G 2   .	0
	I	...       0	0	0 .	0	0	0 .	„ 2 ° G n .

°2_z - дисперсия взвешенных измерений ПФ по l -му спутнику, l - номера только тех спутников, ПФ измерения которых включены в обработку.

На рис. 4 и 5 представлены результаты эксперимента с описанным ФКТ. Условия этого эксперимента полностью соответствовали первому. Здесь полагали, что СКО ПД оD = 6 м, СКО ПС оd = 0,064м/с, а СКО взвешенной величины ПФ оG = 0,003м. На рис. 4 представлена ошибка оценки параметра Ig , а на рис. 5 – ошибка оценки параметра Ug в зависимости от времени наблюдения при N = 12 включенных в обработку ПФ измерений.

Очевидно, что приемлемые точности оценки ухода ПД в ионосфере и тропосфере для спутника, находящегося в зените относительно приемника, получаются практически сразу, что указывает на эффективность данной процедуры. Как показал эксперимент, приемлемые точности параметров I_g и U_g получаются даже при N = 1.

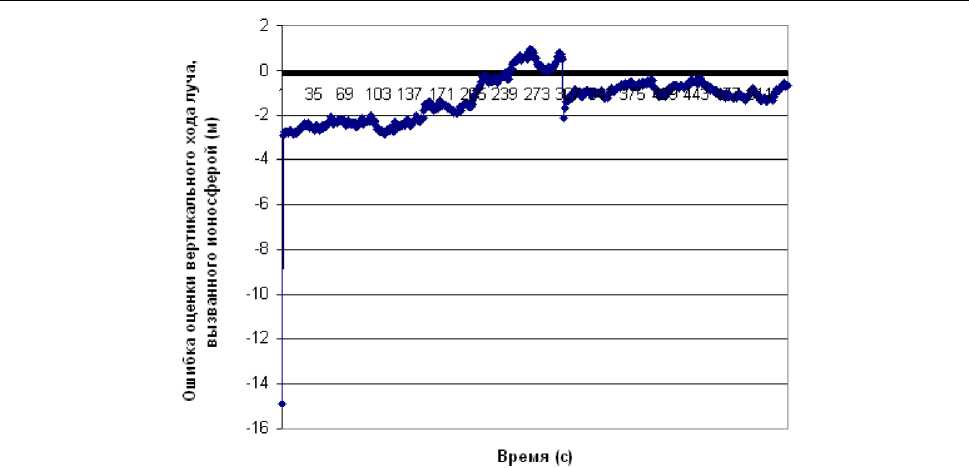
Рис. 4. Зависимость ошибки оценки ФКТ вертикального хода луча, вызванного ионосферой, от времени наблюдения для третьего варианта построения ФКТ

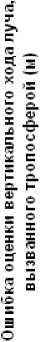
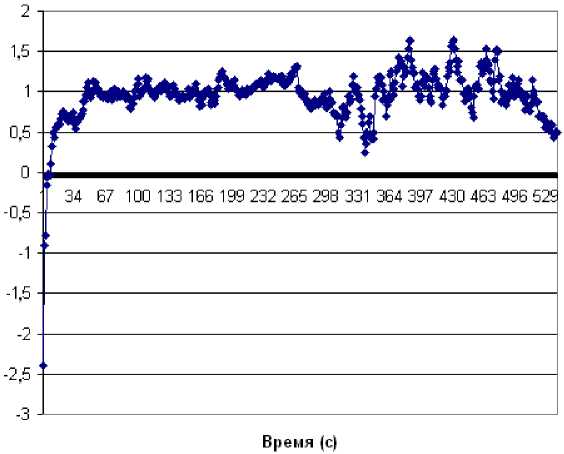
Рис. 5. Зависимость ошибки оценки ФКТ вертикального хода луча, вызванного тропосферой, от времени наблюдения для третьего варианта построения ФКТ

Таким образом, включение в измерения неоднозначных ПФ является наиболее целесообразным способом построения ФКТ, позволяющим наиболее точно оценить ионосферную и тропосферную задержки сигнала СРНС, а также вектор координат и скоростей подвижного объекта в случае использования одночастотного навигационного приемника.