Оценка экономической эффективности инвестиционных институтов на основе моделирования их деятельности

Оценка экономической эффективности деятельности инвестиционных институтов (банков, страховых компаний, пенсионных фондов и пр.) может быть проведена с помощью действующих методик, модифицированных для каждого конкретного вида инвестиционного института. Учесть специфику инвестиционного института при оценке его экономической эффективности можно с помощью экономико-математического моделирования, рассчитав по модели соотношение результатов и затрат или наоборот затрат и результатов деятельности экономического субъекта [4].

Инвестиционные институты относятся к системам массового обслуживания. Данные экономические субъекты выполняют многократно однотипные задачи. Теория массового обслуживания (теория очередей) занимается оценкой функционирования системы при заданных параметрах и поиском параметров, оптимальных по некоторым критериям. Целью анализа на основе теории массового обслуживания является, в конечном счете, отыскание разумной организации обслуживания, обеспечивающей заданное качество.

Аппарат теории массового обслуживания – входной поток, очередь, каналы обслуживания, выходной поток. В роли заявок выступают клиенты, нуждающиеся в той или иной услуге. Роль обслуживающих приборов (каналов) играют работники отдела обслуживания клиентов [3, с. 449].

Независимо от характера процесса, протекающего в системе массового обслуживания, различают два основных вида:

– системы с отказами, в которых заявка, поступившая в систему в момент, когда все каналы заняты, получает отказ и сразу же покидает очередь;

– системы с ожиданием (очередью), в которых заявка, поступившая в момент, когда все каналы обслуживания заняты, становится в очередь и ждет, пока не освободится один из каналов.

Системы массового обслуживания бывают одноканальные и многоканальные. Анализируя модели массового обслуживания, чаще всего ис- пользуют аппарат теории вероятностей, алгебраические и дифференциальные уравнения, а для получения наиболее полного представления об эффективности системы – аппарат имитационного моделирования [1, с. 240].

Имитационная модель – это компьютерная программа, которая описывает структуру и воспроизводит поведение реальной системы во времени. Имитационная модель позволяет получить подробную статистику о различных аспектах функционирования системы в зависимости от входных данных. Наиболее удобный способ построения имитационной модели состоит в использовании автоматизированных средств разработки моделей и проведения исследований на основе программного обеспечение GPSS, Mathcad, Mathlab и т. д. Концепция построения и использования такой программной среды представлена на рис. 1.

Пакет программного обеспечения Mathlab, содержащий в своем составе инструмент визуального моделирования Simulink, позволяет разрабатывать модели, оценивать их характеристики и графически представлять полученные результаты. Simulink – это инструмент, позволяющий достаточно быстро смоделировать систему и получить показатели ожидаемого эффекта и сравнить их с затратами сил на их достижение.

Моделирование в среде Mathlab Simulink требует ввода первоначальных условий и исходных данных. Задача моделирования состоит в определении характеристик системы массового обслуживания на примере работы инвестиционного института (отдел обслуживания клиентов коммерческого банка), при условии, что очередь на обслуживание ограничена пятью клиентами и обслуживаются 2 клиента в минуту.

В блоке «MATLAB Fcn» и «MATLAB Fcn1» задается функция для моделирования потока клиентов – функция «poissrnd(2)». Из количества пришедших клиентов необходимо вычесть количество обслуженных, данное условие реализуется в блоке «Sum», оставшиеся будут накапливаться в блоке «Discrete-TimeIntegrator». Но, чтобы не на-

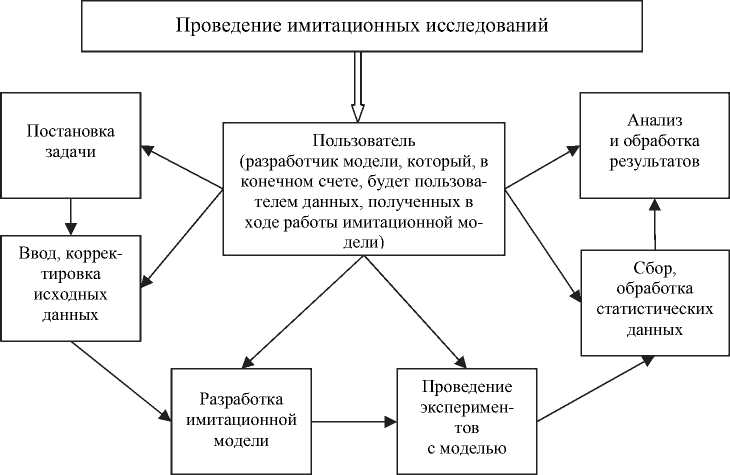
Рис. 1. Построение и использование имитационной модели

капливать отрицательную очередь, необходимо настроить блок «Discrete-TimeIntegrator» – ограничить выходные сигналы, и установить нулевой параметр нижнего предельного значения. За ограничение по очереди отвечают блоки «Relational Operator» и «Switch». Блок «Relational Operator» сравнивает размер очереди с ограничением в 5 клиентов, и, если очередь больше 5, то отправляет управляющий сигнал на блок «Switch». Блок «Switch» – это переключатель, который ограничивает вход клиентов, не пропуская сигнал с блока «MATLAB Fcn», а пропуская 0. В блоке «Switch» необходимо установить пороговое значение 1. В блоках «Fcn» и «Fcn1» необходимо установить функцию «u[2]/u[1]» и «u[1]/u[2]». В модели используется фиксированный шаг, размером 1, логические сигналы выключены. Таким образом, в модели отсчет системного времени ведется через фиксированные интервалы времени, события считаются наступившими в момент окончания этого интервала.

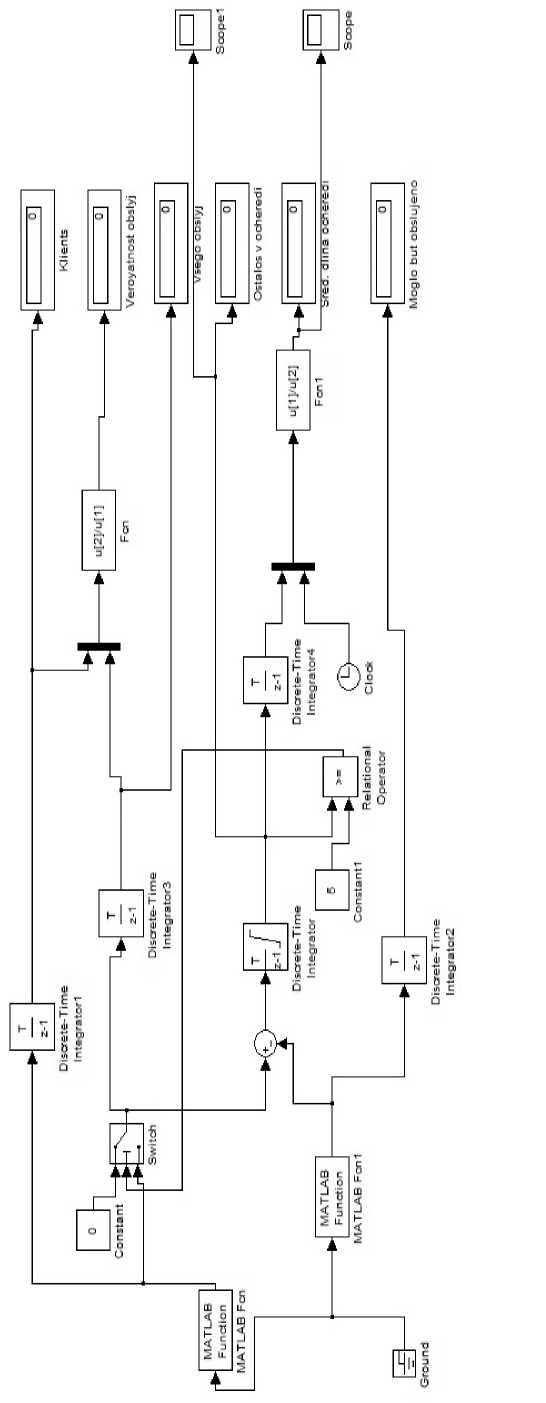
На рис. 2 показана схема модели инвестиционного института.

В ходе анализа данной модели определяются основные характеристики системы: количество обслуженных клиентов, вероятность обслуживания клиентов, общее количество пришедших клиентов, количество оставшихся в очереди клиентов, средняя длина очереди, количество клиентов, которое при заданной мощности каналов обслуживания могла обслужить система. Обобщенные показатели системы представлены в таблице.

Анализ полученных результатов показал, что каналы обслуживания перегружены, в связи с этим имеют место потери от ухода клиентов.

Наблюдение за изменениями сигналов модели в процессе моделирования производится путем графического представления сигналов в функции времени. В среде Mathlab Simulink блок «Scope» отображает графики входящих сигналов после проведения расчетов. В ходе моделирования при заданных параметрах исследования система может обслужить более 200 клиентов в день (рис. 3).

На рис. 4 показан график вероятностей обслуживания клиентов. Вероятности обслуживания клиентов при заданной функции варьируется до 1.

Результаты имитационных экспериментов

№	Количество обслуженных клиентов	Вероятность обслуживания клиентов	Общее количество пришедших клиентов	Количество оставшихся в очереди клиентов	Средняя длина очереди	Количество клиентов, которое могло быть обслужено
1	198	0,8788	174	4	1,76	221
2	178	0,7865	140	5	2,01	200
3	198	0,8283	164	2	2,26	195
4	206	0,8783	180	3	1,78	217
5	202	0,8812	178	6	2,13	225

си

Is I— о z s

о о z z о s J b Ф CD z s к s z cy m s X

о

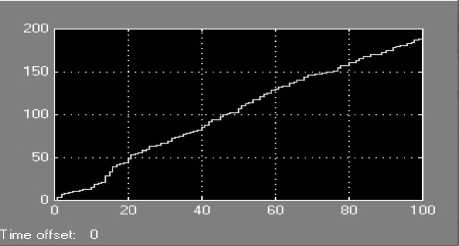
Рис. 3. Поток обслуженных клиентов системы массового обслуживания

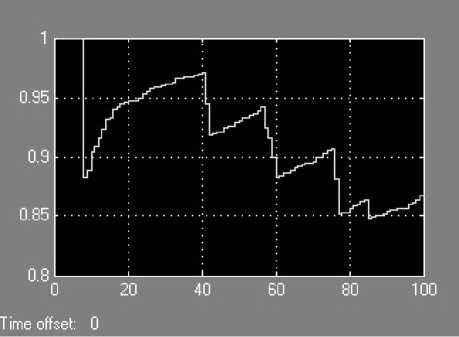
Рис. 4. Вероятности обслуживания заявок в системе массового обслуживания

На рис. 5 показан график средней длины очереди в системе массового обслуживания. В результате моделирования выявлено, что максимальная средняя длина очереди на обслуживание 2,26, что подтверждает перегрузку каналов обслуживания и свидетельствует об уходе клиентов в следствии ожидания.

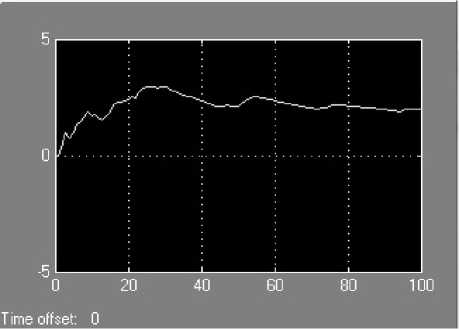
Рис. 5. Средняя длина очереди системы массового обслуживания

Поток необслуженных клиентов обусловливает потери в системе и, тем самым, оказывают негативное влияние на финансовый результат ор- ганизации. На рис. 6 графически отображено состояние очереди в процессе моделирования.

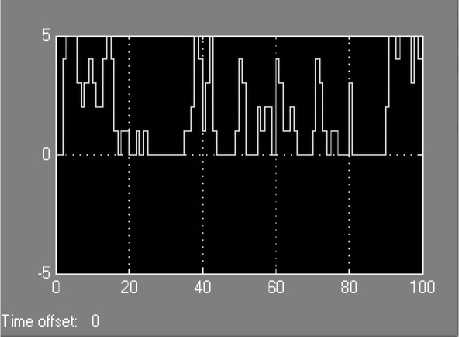
Рис. 6. Очередь в системе массового обслуживания

Экономический смысл имитационного моделирования состоит в определении «слабого звена» в работе системы массового обслуживания и стоимостном выражении потерь в системе, а также разработке рекомендаций руководителю по совершенствованию структуры системы.

Потери в системе массового обслуживания могут возникнуть в связи с простоем каналов обслуживания или перегрузкой каналов. В первом случае необходимо уменьшить количество каналов обслуживания, тем самым сократятся расходы на содержание лишних сотрудников организации. Во втором случае возникает необходимость в увеличении расходов организации на поиск и прием на работу новых сотрудников, но экономический эффект, полученный от обслуживания дополнительных (стоящих в очереди) клиентов, положительно скажется на финансовом результате.

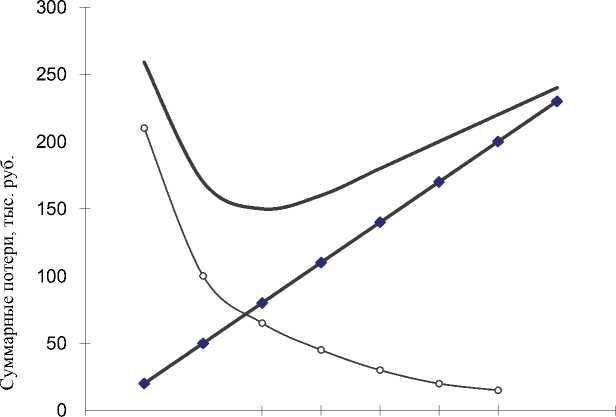
Зависимости расходов на содержание дополнительных каналов обслуживания и потерь от ухода клиентов не обслуженными от числа каналов обслуживания показан на рис. 7.

Издержки на содержание каналов обслуживания прямо пропорциональны числу каналов, а потери от ухода клиентов пропорциональны времени ожидания обслуживания. При увеличении каналов обслуживания потери от ожидания уменьшаются. Оптимальное число каналов обслуживания уменьшит интегральные издержки, связанные с работой системы массового обслуживания. Издержки на содержание каналов обслуживания – это прямые расходы, а издержки от ожидания обслуживания – это альтернативные издержки, т. е. упущенная выгода, и потери от утраты доброго отношения клиентов. Оценка издержек от ожидания обслуживания может быть сделана ориентировочно [2, с. 569].

Стоимостное выражение потерь, возникших вследствие ухода клиентов не обслуженными, по рассмотренным нами исходным данным (рис. 8),

Число каналов обслуживания

♦ Содержание каналов —°— Потери от ухода Полные издержки

Рис. 7. Графики потерь от ухода клиентов и содержания каналов обслуживания

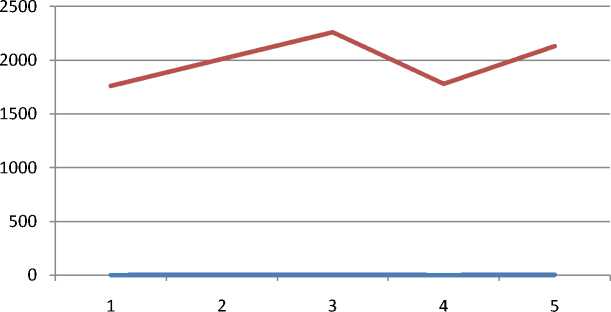
Потери, руб.

Рис. 8. Потери в системе обслуживания можно рассчитать на основе среднего дохода, получаемого в результате обслуживания одного клиента. В модели принято условное значение 1000 руб./клиент.

Представленная имитационная модель является универсальной для инвестиционных институтов разного типа. При этом адаптация модели проводится путём изменения плотности или характера (закона) распределения исходных данных системы. Приведённая модель реализует механизм модельного времени с постоянным шагом. Возможны модификации модели для систем, в которых системное время каждый раз изменяется на величину, строго соответствующую интервалу времени до момента наступления очередного события, при этом закон распределения меняется на экспоненциальный, т. е. моделирующий временной промежуток между наступившими событиями (приход клиента).

Тенденции развития систем имитационного моделирования и практический опыт внедрения их в реальную экономику показывают, что в основе создания новой системы должен стоять конечный пользователь - формулирующий задачи, которые он собирается решить с использованием системы; его уровень квалификации и познания в имитационном моделировании. Использование моделирования, соответствующей квалификации занятых в сфере управления лиц, обеспечит с необходимой оперативностью, при требуемой полноте инфор- мации и минимальных трудовых затратах, получение и практическую реализацию оптимальных управленческих решений.