Оценка электропроводности нанопокрытий интеллектуальных элементов строительных конструкций

Лисиенкова Л.Н., Носова Л.С., Будникова О.А., Титова Ж.О. Оценка электропроводности нанопокрытий интеллектуальных элементов строительных конструкций. Нанотехнологии в строительстве. 2025;17(4):401–414. – EDN: FBNRZK.

В настоящее время во многих отраслях, включая строительную индустрию, возрастает интерес к созданию, производству и применению интеллектуальных («умных» или smart) материалов. Умные материалы становятся более востребованы архитекторами и строителями при проектировании и возведении современных зданий и сооружений [1–2].

Термин «интеллектуальные строительные материалы» на текущий момент не конкретизирован и в различных источниках трактуется неоднозначно [3–4]. Однако можно выявить основные аспекты, определяющие сущность указанных материалов: – во-первых, это материалы, полученные в ходе физической или химической модификации микро-или макроструктуры;

– во- вторых, это материалы, имеющие способность изменять свои исходные свойства по заданному алгоритму при воздействии внешних факторов. Научно-информационный поиск позволил выявить несколько направлений в развитии интеллектуальных строительных материалов, которые можно кратко сформировать в несколько групп:

– модификация традиционных материалов нано-размерными частицами для получения функциональных материалов с заранее заданными свойствами (например, нанодисперсные пластификаторы для самоуплотняющихся бетонов, минеральные нанодобавки для коррозионной прочности и трещиностойкости бетонных смесей) [5–7];

– введение в морфологическую структуру материалов электро-, пьезо- и других проводящих нано-

ИССЛЕДОВАНИЕ СВОЙСТВ НАНОМАТЕРИАЛОВ частиц, обеспечивающих способность материалов реагировать на внешние сигналы и адаптироваться при воздействии различных факторов за счет изменения геометрических, механических, физических свойств (например, слоистые многофункциональные материалы, к которым относятся электро-, термопроводящие, термохромные и фотохромные облицовочные материалы; самовосстанавливаю-щиеся бетоны, «умное» стекло, самоочищающиеся волокнистые материалы и др.) [8];

– создание материалов с градиентной структурой, которые, в отличие от традиционных монолитных строительных материалов, будут максимально приближены к природным натуральным материалам (например, нанодревесина, наноштукатурка и др.) [9–10].

Для получения интеллектуальных конструкций интерес представляют гибкие элементы из различных листовых материалов (пленки, органическое стекло, бумага, профлист и пр.), на которые наносят электропроводящие слои или покрытия. В нанокрасителях используются различные по составу и структуре электропроводящие наночастицы: порошковое или хлопьевидное серебро, углеродные нанотрубки или полимерсодержащие наноразмерные частицы [11]. Для нанопокрытий применяют различные технологии печати, позволяющие создавать на конструкционных элементах различные электронные микросхемы [12].

Для эффективного производства и применения интеллектуальных материалов требуется объективная оценка их свойств и прогнозирование качества на этапах жизненного цикла объектов. Такая потребность, прежде всего, обусловлена новыми свойствами материалов, отсутствием стандартизованных методов и средств объективной оценки их поведения в условиях производства и эксплуатации

Проблема отсутствия методологии прогнозирования закономерностей изменения свойств умных материалов требует углубленных исследований для получения базы новых знаний. Разработка объективных методов исследования обеспечит рациональный выбор рецептуры наночастиц или функциональных компонентов для модификации материалов и позволит прогнозировать их поведение в заданных условиях. Поэтому тематика исследования актуальна и имеет научно-практический интерес в области строительного материаловедения. Объектом исследования в данной работе являются свойства гибких электропроводящих элементов для интеллектуальных конструкций. Предмет исследования – метод оценки электропроводности гибких конструктивных элементов.

Научно-информационный поиск выявил отсутствие объективных методов и средств исследова-

ния и прогнозирования свойств гибких печатных элементов при воздействии факторов производства и эксплуатации. Известные стандартизованные и оригинальные методики испытаний позволяют оценить, в основном, предельные полуцикловые характеристики гибких элементов при их разрушении (например, прочность при растяжении до разрыва, твердость при идентировании и др.) [13–14]. Для оценки деформационных свойств определяют одноцикловые характеристики при растяжении, сжатии, изгибе, кручении [15–17].

Однако результаты таких исследований недостаточно информативны и не позволяют оценить поведение объектов в реальных условиях на различных этапах жизненного цикла. Очевиден факт, что при производстве и эксплуатации исследуемые объекты испытывают не только одноцикловые силовые воздействия (например, при нанесении нанопокрытия способом печати материал подложки подвергается однократному сжатию для создания контакта с электропроводящими наночастицами). Более длительный этап эксплуатации связан с воздействием на элементы небольших по величине, но циклически повторяющихся воздействий внешних механических, физических, химических или комбинированных факторов (силовое, тепловое, атмосферное воздействия, влага, температура, растворы, расплавы и т.п.).

Следует отметить, что циклическое растяжение и сжатие приводят к изменению исходной структуры материалов на микро- и макроуровне без нарушения химических связей. Изменение структурной организации наночастиц и накопление остаточной деформации в элементах будут влиять на геометрические параметры (толщину, плотность и пр.) электропроводящих слоев и, как следствие, – на изменение заданной электрической проводимости элемента [18–19].

Необходимы методы и средства, которые не только обеспечат оценку исходных значений заданных свойств наноматериалов, но и позволят прогнозировать закономерности изменения свойств в процессе эксплуатации. Такой подход обеспечит оптимальный подбор рецептуры наночастиц с учетом условий эксплуатации. В ряде исследований обоснована методология исследования деформационных свойств гибких материалов и слоистых полимеров различного состава и структуры в условиях многоосного циклического растяжения и сжатия [20–21]. Методология основана на комплексном подходе к изучению деформационных характеристик гибких материалов и полимеров. В качестве характеристик приняты обратимая и необратимая части полной деформации [22].

Цель работы заключалась в исследовании закономерности изменения электропроводности печат-

ИССЛЕДОВАНИЕ СВОЙСТВ НАНОМАТЕРИАЛОВ ных элементов для интеллектуальных строительных конструкций в условиях циклического многоосного растяжения.

Для реализации поставленной цели решались следующие задачи :

– провести испытания образцов электропроводящих элементов на циклическое растяжение;

– обработать результаты измерения удельного электрического сопротивления образцов;

– проанализировать закономерности изменения электропроводности печатных элементов в условиях циклического растяжения.

МЕТОДЫ И МАТЕРИАЛЫ

Характеристика объектов исследования

В качестве запечатываемых материалов-подложек для нанесения полупроводниковых нанокомпозиций использовали полимерные материалы различной структуры и способов получения: пленочные, волокнистые и тканые. Полимерная пленка – из полиэтилентерефталата (ПЭТ-Э) толщиной 140±15,0 мкм, изготавливаемая по ГОСТ 24234-80 «Пленка полиэтилентерефталатная. Технические условия».

Волокнистые нетканые полотна, полученные клеевым и механическим способами скрепления, изготавливаемые по ГОСТ 25441-90 «Полотна клееные прокладочные. Общие технические условия», ГОСТ Р 53225-2008 «Материалы геотекстильные. Термины и определения». Нетканые полотна применяются в разных областях строительства для повышения несущей способности и формостабиль-ности различных конструкций, сохраняют свойства при высоких и низких температурах, в агрессивной среде [23, 24].

Ткань армированная для защиты от огня и повышенных температур с нефтемасловодооттталки-вающей отделкой (НМВО) способом пропитки волокон фторуглеродными соединениями по ГОСТ 11209-2014 «Ткани для специальной одежды. Общие технические требования. Методы испытаний». Характеристика материалов представлена в табл. 1.

В качестве электропроводника на образцы материалов (табл. 1) наносилось нанопокрытие методом флексографной печати. Для этого использовали электропроводящие чернила серии 26-8203 Conductive Carbon BF02 (торговая марка Sun Chemical Circuits Touchkey Conductive Ink, производитель США) с наночастицами углерода (производитель «Sun Chemical Corporation» США). Основные характеристики чернил: объемная плотность 1,2 г/см3; удельное сопротивление – 53 мОм×см; вязкость при температуре 25 °С – 10–12 Па×с [11, 25].

Методы исследования структурногеометрических характеристик

В работе использованы стандартные методы подготовки проб для испытаний, оценки показателей структуры и геометрических свойств объектов, представленные в табл. 2. Перед проведением испытаний пробы выдерживали 12 часов в нормальных атмосферных условиях (температура 20±3 °С и относительная влажность 65±5% по психрометру) в соответствии с ГОСТ 10681-75. В этих же условиях проводились испытания.

Методы нанесения электропроводящего покрытия на материалы

Известны различные способы нанесения электропроводящих композиций: глубокая, офсетная, трафаретная, флексографская, струйная [26, 27]. В работе использован способ трафаретной печати для нанесения покрытия. На поверхность запечатываемых материалов (табл. 1) краска подается через печатные формы (оттиски). Печать форм выполняли на ручном трафаретном станке карусельного типа «ARGON» [28]. Толщина электропроводящего покрытия после высыхания 0,1±0,05 мм

Методы оценки электропроводности

Электрическое сопротивление измерялось цифровым мультиметром РЕСАНТА DT-181 в соответствии с методикой ГОСТ 3345-76 «Кабели, провода и шнуры. Метод определения электрического сопротивления изоляции». Техническая характеристика мультиметра представлена в табл. 3. Схема измерения сопротивления исследуемых объектов представлена в работе [29].

Методы исследования деформации элементов при циклическом многоосном растяжении

Испытания проводили на автоматизированном устройстве [37]. Основные характеристики устройства: – максимальная нагрузка на пробу – до 4,0 кг;

– максимальное количество циклов за один период испытания – 255 циклов;

– максимальное время нагружения (отдыха) в цикле – 255 с;

– максимальное количество периодов испытания – не ограничивается;

– абсолютная погрешность измерения: ± 10 мкм;

– точность измерения величины провисания пробы – 2 %;

– тип датчика измерения перемещения и толщины пробы: дифференциальный фотоэлектрический;

ИССЛЕДОВАНИЕ СВОЙСТВ НАНОМАТЕРИАЛОВ тип двигателя: шаговый электродвигатель, 220 В; скорость линейного перемещения: 2…5 мм/с;

размеры прибора – 350×250×400 мм, масса – не более 5 кг;

зажимные кольца для фиксации пробы D = 25, 40, 60 мм (рис. 1 а);

съемные наконечники индентора d = 15, 20, 25, 35, 55 мм (рис. 1 б);

– проба размерами не менее 10×10 см, толщина 0,01…5,0 мм (рис. 1 а);

– грузы массой от 0,2…4,0 кг.

Теоретический анализ деформации и расчетные формулы напряжений при многоосном растяжении гибких оболочек представлены в работах [29]. По экспериментальным данным строятся эмпирические кривые изменения величины провисания

Таблица 1. Характеристика материалов для нанесения нанопокрытия (серия 26-8203 Conductive Carbon BF02 )

№ п/п	Показатель	Образец 1	Образец 2	Образец 3	Образец 4	Образец 5
		Пленка ПЭТ-Э, ГОСТ 24234	Полотно нетканое арт. 45519 ГОСТ 25441	Геотекстиль GP200 арт. 02003 ГОСТ Р 53225	Геотекстиль GP300 арт. 02005 ГОСТ Р 53225	Ткань арт. 15406а-В ГОСТ 11209
1	Состав	Полиэтилентереф-талат (ПЭТ)	Волокно полиэфирное 80%, бикомпонентное – 20%	Полиэфирное волокно – 100%	Полиэфирное волокно – 100	Волокно хлопковое 95%, полиамидное – 5% + антистатическая нить;
2	Метод изготовления	Экструзия расплава с последующей ориентацией, термофиксацией и охлаждением	Клеевой с последующим термокаландрированием	Иглопробивной способ с последующей термофиксацией (термокаландрированием)		тканый – саржевое переплетение, отделка НМВО
3	Толщина, мм / (мкм)	0.14±0.015 / (140±15,0)	0,36±0,05	0,67±0,10	2,23±0,33	0,47±0,07
4	Поверхностная / (Объемная) плотность, г/м2 / (кг/м³)	196 / (1390–1400)	50±10	200±40	300±45	265±0,52
5	Модуль упругости, не менее, МПа	137–147	1,0–2,0	4,5–7,5	10–12	0,5 • 10–3
6	Прочность при разрыве, МПа (Н/5 см)	157–172 МПа	40–50 Н/5 см	300±36 Н/5 см	450±54 Н/5 см	650±32,5 Н/5 см
7	Относительное удлинение при разрыве, не менее, %	70–100	20–30	50–60	120–160	20–30
8	Удельное объемное электрическое сопротивление, Ом*см, не менее	1х1014	–	–	–	–
9	Температура эксплуатации, °С	–70…+150	–65…+80	–65…+80	–65…+80	+250* (температура воспламенения)
10	Усадка, % (при 155 °C) не более	3	2	2	2	3

ИССЛЕДОВАНИЕ СВОЙСТВ НАНОМАТЕРИАЛОВ

Таблица 2. Стандарты на методы исследований объектов

№	Выполняемые исследования	№ ГОСТ	Название документа
1	Отбор образцов нетканых полотен	ГОСТ 13587-77	Полотна нетканые и изделия штучные нетканые. Правила приемки и метод отбора проб
2	Отбор образцов пленочных материалов	ГОСТ 24234-80	Пленка полиэтилентерефталатная. Технические условия
3	Отбор образцов ткани	ГОСТ 20566-75	Ткани и штучные изделия текстильные. Правила приемки и метод отбора проб
4		ГОСТ 29104.0-91	Ткани технические. Правила приемки и метод отбора проб.
5	Подготовка проб для испытаний	ГОСТ 10681-75	Материалы текстильные. Климатические условия для кондиционирования и испытания проб и методы их определения
6	Определение толщины, мм	ГОСТ 12023-2003	Материалы текстильные и изделия из них. Метод определения толщины
7	Оценка структурных характеристик: поверхностная плотность г/м2; длина, мм; ширина, мм	ГОСТ 3811-72	Материалы текстильные. Ткани, нетканые, полотна и штучные изделия. Методы определения линейных размеров, линейной и поверхностной плотностей
8		ГОСТ 15902.2-2003 (ИСО 9073-2:1995)	Полотна нетканые. Методы определения структурных характеристик
9	Определение влажности, %	ГОСТ 3816-81	Полотна текстильные. Методы определения гигроскопических и водоотталкивающих свойств

Таблица 3. Основные характеристики мультиметра РЕСАНТА DT-181

№	Измеряемый параметр	Единицы измерения	Диапазон измерения	Погрешность, %
1	Переменное напряжение	Вольт	200–750	1,5
2	Постоянное напряжение	Вольт	2–1000	0,8
3	Сила постоянного тока	Ампер	до 10	1,2
4	Сопротивление	МОм	до 2	1,0

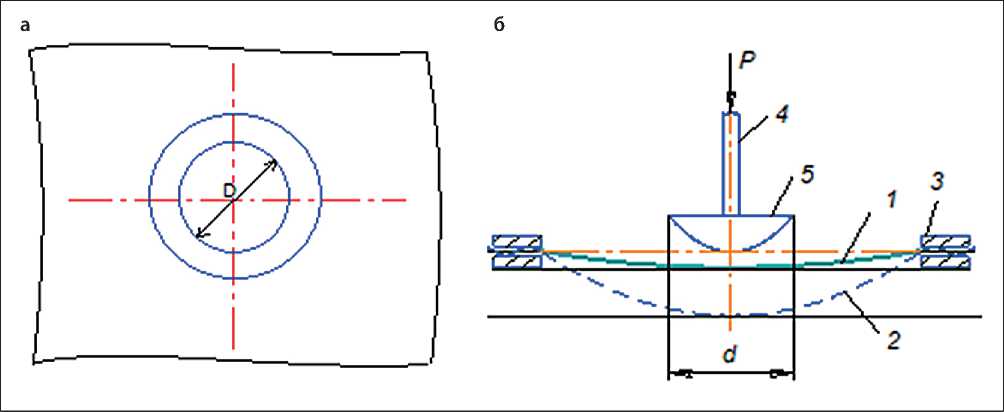
Рис. 1. Форма пробы материала (а) и схема испытания (б). Положение пробы: D – рабочий размер пробы, мм; 1 – до растяжения, 2 – при нагружении, 3 – зажимное приспособление, 4 – индентор, 5 – съемный наконечник [29, 30]

ИССЛЕДОВАНИЕ СВОЙСТВ НАНОМАТЕРИАЛОВ пробы при нагружении и отдыхе h(t). Расчет доли обратимой и необратимой деформации выполняли по формулам:

– доля условной необратимой (остаточной) деформации:

ε необр = h i / h макс , i ≥ 30,

где h _i – среднее значение 10-ти последних измерений величины провисания пробы после отдыха, мм;

h _макс – значение величины провисания пробы при нагрузке, мм;

– доля условной быстро обратимой деформации:

ε_обр = ( h_макс – h ₁) / h_макс ,

где h ₁ – значение первого измерения величины провисания пробы после снятия нагрузки, мм.

Методы обработки результатов испытаний

Результаты экспериментов обработаны согласно ГОСТ Р 8.736-2011 «Государственная система обеспечения единства измерений. Измерения прямые многократные. Методы обработки результатов измерений. Основные положения», ГОСТ Р ИСО 16269-4-2017 «Статистические методы. Статистическое представление данных. Часть 4. Выявление и обработка выбросов». По результатам экспериментальных данных определили основные статистические характеристики по известным формулам, представленным в табл. 4.

Для проверки однородности дисперсии и воспроизводимости эксперимента при одинаковой повторности опытов рассчитывали значение критерия Коч-рена G _к. Адекватность модели изучаемого процесса проверяли по критерию Фишера F _р. Если расчетное значение критерия Фишера F _p меньше табличного F _m, то гипотеза об адекватности не отвергалась.

Согласно критериям оценки точности по теории математической статистики, достоверность результатов эксперимента принималась при условии, если величина относительной среднеквадратической ошибки не превышала 10% (при достоверности 0,95), а коэффициент вариации – не более 10%.

РЕЗУЛЬТАТЫ ИСПЫТАНИЙ

В экспериментальной части проведены испытания подготовленных образцов на многоосное циклическое растяжение при следующих параметрах: – диаметр рабочей зоны испытуемого образца D =

40 мм;

– диаметр основания индентора, d = 25 мм;

– растягивающее усилие Р_ц , = 10 Н;

Таблица 4. Обработка результатов эксперимента

№	Статистические характеристики	Расчетные формулы
1	Среднее арифметическое	х = --Ух
2	Дисперсия	л n                2 52=^Х^-^)
3	Стандартное отклонение	V 77-1
4	Коэффициент вариации	C = y-100%
5	Абсолютная ошибка	m = —= y/n
6	Относительная ошибка	^ = ^•100%
7	Критерий Кочрена	max К    n i=l
8	Критерий Фишера	77 _ ^ad ~   2

– время растяжения пробы t_нагр = 5 с;

– время отдыха пробы в каждом цикле растяжения релакс с;

– общий период нагружения пробы n = 50–300 циклов, измерения проводили после 50, 100, 150, 200, 250, 300 циклов нагружения.

Сущность испытания заключалась в циклическом многоосном растяжении пробы, закрепленной в шаблон по контуру (см. рис. 1, б) и измерении величины провисания пробы при нагружении и отдыхе. После каждого периода растяжения измеряли толщину и электрическое сопротивление проб.

По первичным результатам измерения величины провисания проб после циклов растяжения во встроенном в прибор программном обеспечении автоматически рассчитывалась полная деформация, методика расчета представлена в работах [29, 30]. Компоненты деформации рассчитывались по формулам (1), (2). Результаты приведены в табл. 5. Результаты измерения толщины приведены в табл. 6. Среднеквадратическая ошибка результатов составила 0,2–3,0 %; дисперсия 0,05–0,20; коэффициент вариа-

ИССЛЕДОВАНИЕ СВОЙСТВ НАНОМАТЕРИАЛОВ

Таблица 5. Результаты оценки деформации проб с электропроводящим слоем при циклическом растяжении

№	Образец	Циклы	Деформация, доли		Дисперсия среднего выборочного, S b2 , мм2	Коэффициент вариации С в, %	Ошибка опыта, m x, %
			обратимая	необратимая
1	Пленка ПЭТ-Э, ГОСТ 24234	50	0,89	0,11	0,03	6,66	0,23
		100	0,93	0,07	0,04	17,39	0,31
		150	0,89	0,11	0,05	11,65	0,42
		200	0,88	0,12	0,06	13,12	0,53
		250	0,91	0,09	0,05	15,52	0,5
		300	0,92	0,058	0,04	13,79	0,36
2	Полотно нетканое арт. 45519 ГОСТ 25441	50	0,26	0,74	0,13	1,83	2,04
		100	0,81	0,19	0,12	7,1	2,12
		150	0,91	0,09	0,11	5,2	2,01
		200	0,78	0,22	0,09	4,3	1,67
		250	0,93	0,07	0,11	16,1	2,12
		300	-*	* при 300 циклах – разрушение образца
3	Геотекстиль GP200 арт. 02003 ГОСТ Р 53225	100	0,92	0,08	0,04	8,80	0,46
		150	0,95	0,05	0,05	16,00	0,60
		200	0,96	0,04	0,03	9,11	0,36
		250	0,94	0,06	0,04	8,80	0,49
		300	0,96	0,04	0,05	12,40	0,63
4	Геотекстиль GP300 арт. 02005 ГОСТ Р 53225	50	0,65	0,35	0,06	3,42	0,62
		100	0,89	0,11	0,05	9,50	0,52
		150	0,90	0,10	0,05	10,46	0,55
		200	0,96	0,04	0,05	20,50	0,55
		250	0,95	0,05	0,04	17,09	0,45
		300	0,94	0,06	0,04	11,97	0,45
5	Ткань арт. 15406а-В ГОСТ 11209	50	0,59	0,41	0,07	2,24	0,92
		100	0,91	0,09	0,05	8,47	0,67
		150	0,49	0,51	0,05	1,26	0,66
		200	0,91	0,08	0,05	8,62	0,69
		250	0,92	0,08	0,05	10,7	0,69
			0,94	0,06	0,05	12,19	0,69

Таблица 6. Результаты оценки толщины (мм) проб с электропроводящим слоем после циклов растяжения

Циклы	Толщина проб, мм
	Пленка ПЭТ-Э, ГОСТ 24234	Полотно нетканое арт. 45519 ГОСТ 25441	Геотекстиль GP200 арт. 02003 ГОСТ Р 53225	Геотекстиль GP300 арт. 02005 ГОСТ Р 53225	Ткань арт. 15406а-В ГОСТ 11209
0	0,17	0,40	0,96	2,47	0,57
50	0,17	0,36	0,95	2,41	0,56
100	0,17	0,32	0,93	2,36	0,56
150	0,17	0,31	0,91	2,31	0,55
200	0,17	0,26	0,90	2,27	0,55
250	0,17	0,21	0,88	2,24	0,55
300	0,16	-*	0,87	2,21	0,54

ИССЛЕДОВАНИЕ СВОЙСТВ НАНОМАТЕРИАЛОВ

Таблица 7. Результаты измерения сопротивления электропроводящего покрытия тестируемых образцов

Циклы	Электрическое сопротивление, Ом
	Пленка ПЭТ-Э (образец 1)	Полотно нетканое (образец 2)	Геотекстиль GP200 (образец 3)	Геотекстиль GP300 (образец 4)	Ткань арт. 15406а-В (образец 5)
0	53,8	109,0	64,1	25,2	47,3
50	130,2	750,9	93,3	25,3	85,5
100	95,6	1675,1	118,1	27,4	93,3
150	96,3	3679,4	131,4	28,5	100,8
200	100,4	4397,4	154,3	30,2	130,0
250	105,9	4963,9	160,1	36,3	131,1
300	162,7	-*	180,4	41,4	132,8

* При испытании образца № 2 (табл. 1, 5–7) произошла необратимая деформация с разрушением всей системы из электропроводящего слоя и материала, поэтому измерить сопротивление после 300 циклов растяжения не удалось.

ции 10–12 %. В некоторых случаях коэффициент вариации достиг 16–20%, что допустимо для нетканых материалов по причине большей неравномерности их структуры по сравнению с пленками и тканями.

Сопротивление электропроводящего покрытия измерялось после каждых 50 циклов нагрузки, не вынимая пробу из формы-шаблона. Результаты измерения представлены в табл. 7.

ОБСУЖДЕНИЕ

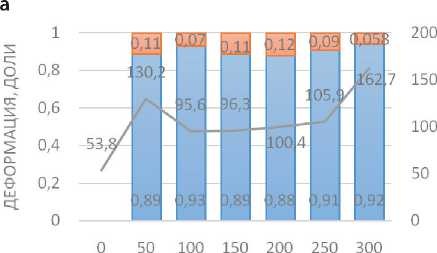
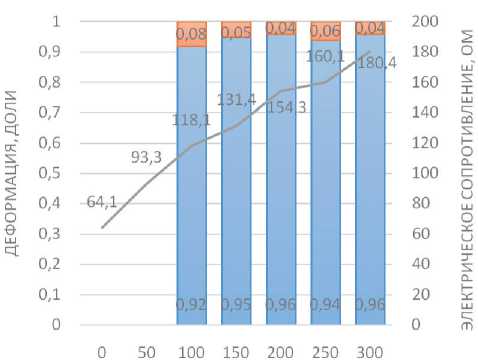
Анализ результатов испытания образцов №№ 1–5 (табл. 1, 5–7) показал, что наибольшая величина остаточной деформации наблюдается после 50 циклов растяжения. Диаграммы изменения компонент деформации и сопротивления образцов представлены наглядно на диаграммах рис. 2.

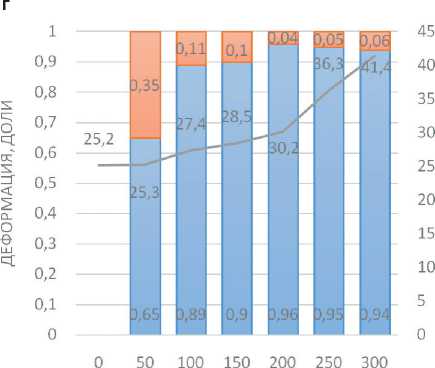
Максимальное значение остаточной деформации 0,74 (доли) после 50 циклов имеет нетканое полотно исходной толщиной 0,36 мм с электропроводящим слоем (образец № 2). Дальнейшая нагрузка от 250 до 300 циклов привела к разрушению образца (см. табл. 5). Максимальное увеличение электрического сопротивления (в 8–10 раз) у образца № 2 наблюдалось после первых 50 циклов растяжения (табл. 7, рис. 2 б).

У образца № 3 (исходная толщина подложки 0,67 мм) после 100 циклов остаточная деформация несущественно увеличилась на 8–10% (табл. 1, 5–7). Дальнейшие циклы растяжения не привели к росту остаточной деформации, что объясняется релаксацией образца и его упругим восстановлением. Электрическое сопротивление образца № 3 после 50 циклов увеличилось на 35–40 %, а после 300 циклов растяжения – почти в 2 раза (см. табл. 7). Следует отметить у образца № 3 относительно равномерный прирост сопротивления в пределах 15–20% после каждого периода растяжения (рис. 2 в).

После 50 циклов растяжения образца № 4, выполненного на нетканом полотне толщиной 2,23 мм (табл. 1), остаточная деформация составила 0,35 (доли), дальнейшее растяжение практически не привело к увеличению остаточной деформации данного образца (табл. 5). Электрическое сопротивление образца № 4 увеличилось с 25 Ом до 41 Ом соответственно после 50 и 300 циклов растяжения, что в целом составляет 50-60% (табл. 7, рис. 2 г).

Остаточная деформация образца № 5 (табл. 1, 5) увеличилась после первых 50 циклов на 40%. Далее до 100 циклов образец № 5 «работает» как упругая система. После 150 циклов – остаточная деформация увеличивается (45–50%) и при последующих циклах образец № 5 работает «упруго» (табл. 5). Это объясняется особенностями релаксационных процессов ткани-подложки данного образца № 5. Циклические нагрузки вызывают два и более периодов релаксации тканых полотен – вследствие деформации нитей в переплетении и деформации волокон в нитях ткани.

Электрическое сопротивление образца № 5 равномерно увеличивалось на 10–20% после каждых 50 циклов растяжения. В целом, сопротивление данного образца в периоды 50-300 циклов увеличилось на 45% (рис. 2 д).

Циклическое растяжение образца № 1, выполненного на пленке ПЭТ-Э толщиной 0,14 мм (табл. 1), не изменило обратимую часть деформации. Монолитная структура пленки, упругое поведение образца после 300 циклов растяжения объясняется монолитной структурой пленки (табл. 5). Однако электрическое сопротивление образца № 1 изменялось неоднозначно: после 200 циклов – уменьшилось с 130 до 100 Ом. После 200 циклов наблюдалось увеличение сопротивления до 162,7 Ом (см. табл. 7). Нестабильная динамика изменения

ИССЛЕДОВАНИЕ СВОЙСТВ НАНОМАТЕРИАЛОВ

I Деформация обратимая, доли

।    । Деформация необратимая, доли

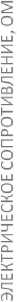
б

Электическое сопротивление, Ом

в

ЭЛЕКТРИЧЕСКОЕ СОПРОТИВЛЕНИЕ, ОМ            ЭЛЕКТРИЧЕСКОЕ СОПРОТИВЛЕНИЕ, ОМ

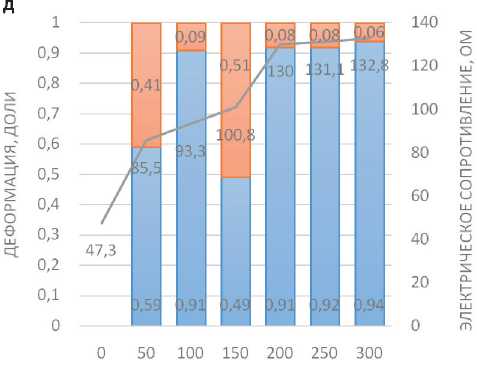
Рис. 2. Диаграммы изменения деформации и сопротивления после циклов многоосного растяжения образцов: а – пленка ПЭТ-Э; б – полотно нетканое арт. 45519; в – геотекстиль GP200; г – геотекстиль GP300; д – ткань арт. 15406а-В

ИССЛЕДОВАНИЕ СВОЙСТВ НАНОМАТЕРИАЛОВ сопротивления электропроводящего покрытия на пленке, возможно, связана с уплотнением покрытия под давлением индентора, что может приводить к увеличению сопротивления. С другой стороны, уплотнение покрытия увеличивает его жесткость, уменьшает площадь и силу сцепления с поверхностью пленки, что приводит в конечном итоге к отслаиванию и/или разрушению электропроводящего покрытия и увеличению сопротивления. Такая нестабильность поведения данного образца при циклических нагрузках может существенно снижать качество готовых конструктивных элементов при эксплуатации (рис. 2 а).

Таким образом, деформация образцов изменяется в целом от 8% до 75% и зависит от структуры исходных материалов и системы «покрытие-подложка». Очевидно, что структура электропроводящего слоя зависит от исходных материалов. Для установления наличия связи между деформацией и электрическим сопротивлением выполнены корелляционный и регрессионный анализы независимых величин: Х – деформация после циклов растяжения, доли; У – электрическое сопротивление, Ом. Анализ коэффициентов корреляции (см. табл. 8) позволяет утверждать о наличии сильной степени связи между электрическим сопротивлением и циклической деформацией исследуемых объектов, так как коэффициент корреляции r > 0,5.

С помощью аппроксимации найдены зависимости электрического сопротивления от деформации в условиях циклического растяжения для различных материалов: входной фактор Х – деформация после циклов растяжения, доли; выходной фактор У – электрическое сопротивление, Ом. Эмпирические уравнения регрессии аппроксимировали полиномом второй степени, коэффициенты, уравнения и критерий адекватности – в табл. 8.

Анализ коэффициентов уравнений регрессии (табл. 8) с учетом физики исследуемых процессов позволяет предположить, что в уравнениях коэффициент при х² определяет динамику и величину изменения сопротивления, а коэффициент при х –

момент времени (циклы деформации образца), при котором начинается интенсивное изменение электрического сопротивления образца.

Таким образом, анализ результатов исследований подтверждает различный механизм структурной организации связей, образуемых между электропроводящим покрытием и материалом подложки. Связь между слоями в системе композита «покрытие – подложка» зависит от структуры подложки (при нанесении одного и того же покрытия). Можно выделить три основных типа взаимодействия слоев и, соответственно, спрогнозировать поведение гибких конструктивных элементов в эксплуатации.

Покрытие на сравнительно жестких монолитных пленках (которые традиционно применяют для гибких резисторов) формируется на поверхности пленки без диффундирования в структуру подложки. В данном случае высока вероятность отслаивания покрытия от подложки при циклическом внешнем силовом воздействии, это может привести к искажению либо полной потере электрического сигнала конструктивным элементом в эксплуатации.

На тонких нетканых материалах (образец 2) вследствие диффузии частиц электропроводящей композиции по толщине возможно полное пропитывание подложки. В этом случае при эксплуатации такого элемента возможен контакт со сторонними электропроводящими элементами, на которые может уходить электрический сигнал либо утечка электрического тока. Утечка электрического тока -наиболее опасный вариант при эксплуатации такого конструктивного элемента. Можно утверждать, что тестируемое полотно толщиной 0,37 мм (образец 2) не подходит для создания гибких электропроводящих элементов.

Нетканые полотна и ткани толщиной более 0,47 мм (образцы 3, 4, 5) представляют наибольший интерес для изготовления гибких элементов. Это подтверждается удовлетворительными результатами испытаний. В данном случае электропроводящий слой формируется на поверхности подложки

Таблица 8. Анализ зависимости сопротивления от деформации образцов в условиях циклического многоосного растяжения

№	Образец	Коэффициент корреляции	Уравнение регрессии	Критерий адекватности R2
1	Пленка ПЭТ-Э	0,51	y = 469,19x2–221,28x+123,52	0,628
2	Полотно нетканое арт. 45519	0,78	y = 59202x2–88366x+33638	0,943
3	Геотекстиль GP200 арт. 02003	0,78	y = 65,394x2–400,73x+29,771	0,965
4	Геотекстиль GP300 арт. 02005	0,65	y = 218,44x2–179,7x+62,073	0,953
5	Ткань арт. 15406а-В	0,66	y = 146,07x2–155,93x+128,07	0,883

ИССЛЕДОВАНИЕ СВОЙСТВ НАНОМАТЕРИАЛОВ и частично диффундирует по ее толщине. Такой механизм взаимодействия слоев в композите «покрытие – подложка» обеспечивает относительную стабильность значений сопротивления.

Однако при получении покрытия на полотнах толщиной более 2 мм (образец 4) возможны экономические и технологические трудности: требуется 2–3 прогона для получения сплошного оттиска, что увеличивает расход электропроводящей композиции; готовый элемент получается с другими электрическими и механическими свойствами. Поэтому оптимальным выбором для гибких электропроводящих элементов будут полотна толщиной 0,5–0,7 мм (образцы 3, 5).

ЗАКЛЮЧЕНИЕ (ВЫВОДЫ)

Исследование позволило получить объективную оценку изменения электропроводности покрытий интеллектуальных элементов строительных конструкций в условиях циклического растяжения. На основе научно-информационного поиска и предварительных исследований выбраны способ нанесения электропроводящего покрытия: трафаретная печать и электропроводящая полимерная композиция с углеродными наночастицами. Образцы гибких материалов в системе «покрытие-подложка» отличались составом и структурой – пленки, полотна нетканые, ткани толщиной 0,14–2,23 мм. Определены параметры испытаний образцов в условиях циклического многоосного растяжения: 50–300 циклов, циклическая нагрузка 10 Н, время нагрузки и отдыха – по 5 сек, измерения толщины,

деформации и сопротивления проводились через каждые 50 циклов.

Результаты испытаний показали, что деформация и ее компоненты изменяются неоднозначно. Необратимая часть деформации образцов изменялась в целом от 8% до 75% и зависит от структуры материалов, на которые наносилось покрытие. Толщина печатных элементов изменялась в целом от 6% до 100% и также зависит от структуры исходных материалов. Электрическое сопротивление образцов изменялось от 25 до 5 кОм и зависит от параметров испытаний, структуры композита «покрытие – подложка». Корреляционный анализ подтвердил сильную степень связи между величиной электрического сопротивления и деформацией образцов. Величина коэффициента корреляции 0,60–0,78. С помощью аппроксимации найдены эмпирические уравнения, которые могут использоваться при прогнозировании надежности гибких электропроводящих элементов в условиях циклического растяжения, имитирующих условия эксплуатации.

Сравнительный анализ результатов испытания объектов в условиях циклического растяжения позволил рекомендовать для гибких электропроводящих элементов нетканые полотна и ткани толщиной 0,5–0,7 мм (образцы 3, 5). Таким образом, полученные результаты показали, что методика циклического растяжения может быть рекомендована для рационального выбора и прогнозирования поведения гибких электропроводящих элементов при проектировании, производстве и эксплуатации интеллектуальных строительных конструкций зданий и сооружений.