Оценка ковариационной матрицы для временных рядов различных частотностей

Для случая, когда временные ряды имеют одинаковую частотность, различные оценки ковариационных матриц изучаются во многих работах (см., например, [5-7; 9-11]).

В данной работе изучается оценка ковариационной матрицы, построенная для рядов различной частотности. Пример такого рода временных рядов изображён на рис. 1.

В разделе 2 даётся описание оценки ковариационной матрицы из работы [11] для случая, когда все временные ряды имеют одинаковую частотность. В разделе 3 приводится обобщение этой оценки для временных рядов различных частотностей. В разделе 4 устанавливается положительная полуопределённость и состоятельность предложенной оценки. При этом используется результат, относящийся к так называемым последовательностям со свойством перемешивания (с ними можно ознакомиться, например, в [1-2] или приложении к [3]).

Численные примеры применения рассматриваемой оценки приведены в [3; с. 8-9, 14-20] и [12; с. 16-32].

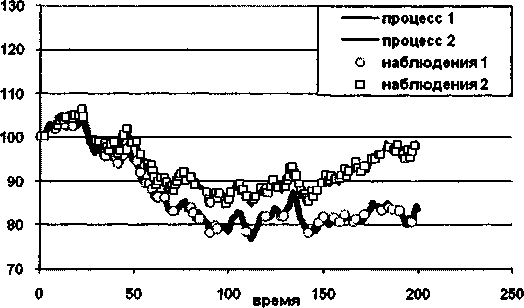
Рис. 1. Наблюдения двух непрерывных случайных процессов в нерегулярные моменты времени (различные для двух процессов)

• 2.    Конструкция оценки ковариационной матрицы в случае, когда пропущенных данных нет

Примером многомерного временного ряда, компоненты которого доступны с различной частотностью (символом • обозначены места, где значение недоступно), может быть ряд

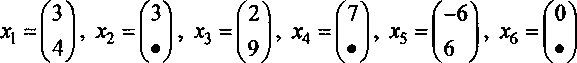
Для случая, когда исходные временные ряды имеют одинаковую частотность, задача, аналогичная рассматриваемой в данной работе, ставится следующим образом.

Будем обозначать через N множество натуральных чисел, через Z множество целых чисел, через R" и-мерное евклидово пространство. Рассмотрим последовательность x_t зависящих от параметра случайных векторов. Более точно, пусть ^,F,P^ - вероятностное пространство, т.е. для каждого подмножества А, входящего в ст -алгебру F, AeF , определена вероятность Р^А^. Пусть 0 с R^p - компактное выпуклое множество. При каждом t е Z рассматривается функция х₍ : Q х 0 -> R" , которая для любого 6 е &  является измеримой функцией аргумента ю е Q, т.е. является (их1) случайным вектором. Этот случайный вектор мы будем обозначать иногда как х₍ (®,0), иногда как x_t (0), иногда как х,.

Пусть для некоторого г е Z, г > О, определена измеримая функция

ф_: ^”(r+i) _> _Rq .

Будем использовать обозначение

Pt =Ф^х„х1_х,...,х1_тУ где t е Z . Далее для упрощения изложения будем считать, что при любом 0 е 0 (9 х 1) случай ные векторы pt имеют нулевые ожидания:

E^pt^ = 0, ^teZ.

Определим (^xl) случайный вектор R_T=—== ^p_t и рассмотрим его ковариационную матрицу S_T . Т.к. E^p_t ) = 0, матрица S_T имеет вид

S Т=Е

ml/2 ^<

^     /=1

ThZp.

Ньюи и Вест в [11] строят оценку

„      A      ”       / А      А X          А      1 Г

8_Т = Qo + ^km\Qk +бл)>где Q_k =- £ p_tp'_t__k . к=\ ^х '        ^т м

При некоторых условиях, в частности, на веса w^ (точные формулировки приведены в разделе

• 5)    матрица S_T является положительно полуопределённой и

• ST — ST ———>0 при Т—>оо.

• 3.    Конструкция оценки ковариационной матрицы в общем случае

Отметим, что если существует предел1 5 = lim ST - некоторая (^ х ^) матрица2, то этом случае Т—>оо можно говорить о состоятельности ST при Г -> оо. Если этот предел не существует, то под со стоятельностью оценки, следуя, например, [11], мы понимаем ST -ST ——>0 при Т -» оо.

Для последовательности х,, определённой так же, как и ранее, рассмотрим множество точек (i,t) с целыми координатами, / = 1,2,...,и, t е Z. Пусть М_х -подмножество этого множества. Обозначим z-ю компоненту случайного вектора х, как х^ . Будем говорить, что случайная величина х^ доступна, если (z,/) е М_х, и что не доступна, если (i,f) & М_х .

Запишем равенство pt = ®(xz,xz_15...,xz_r) покомпонентно: рУ =                               , j = V,q, и будем говорить, что функция Ф^ постоянна по (пк + z)-й компоненте, к = 0,1,...,r;i = 1,2,...,п, если для V(xz,x/_1,...,xz_r)e Rm выполнено равенство: фО')/’у(1) у(2) Г(П) y(D у(2) АП у(")\_

• (2)    W (1) (2)    ₀     (n)\

~ ^ \^At »^At ••***(  9**/—I»-*/—1 9^ee»>^V>^eee9-*;—f I •

Назовём случайную величину р^ =Ф^ух^\х^²\.^^п\х^2_х,х^,...,х^_1г.^ доступной, если для данных t и j функция Ф^⁾^¹⁾,хр⁾..д:р⁾,х%,хрр...,хр⁾_к...,хр^ постоянна по всем недоступным случайным величинам среди её аргументов х^, к = О..т, i = 1 ..п . В противном случае назовём случайную величину рр^ недоступной.

Рассмотрим множество точек (у,/), j = 1,2...9 , teZ. Пусть его подмножество М_р определено таким образом, что элемент (y,z) принадлежит М_р тогда и только тогда, когда случайная величина рр^ является доступной.

При построении оценки мы будем использовать лишь доступные случайные величины рр^, для которых t = 1 ...Т.

Т.к. каждый случайный вектор х₍ в {*_z}^_r является функцией tyeQ и 0с0, а каждый случайный вектор p_t из {р,}^ является функцией некоторых случайных векторов из {х,}^__г,мы можем писать x_t = x_t (<э,0), p_t = p_t ро,&}.

Определим А_т как (^ х 1) случайный вектор с компонентами

Тогда, если все компоненты всех рассматриваемых векторов p_t доступны, случайный вектор А_г совпадает со случайным вектором R_T . Определим ковариационные матрицы случайных векторов А_т:

Z_r=E(A_rA^)                              (3)

(напомним, что Е (А_т ) = 0).

Поскольку случайный вектор А_т является сложной функцией вида А_т ^/?,((У,5)^), матрица Z_T является функцией 0, т.е. Z_T = Z_T (5).

Задача данной работы состоит в построении по доступным компонентам случайных векторов {/Э(}^ последовательности положительно полуопределенных случайных матриц Z_T, таких, что Z_T -Z_T ———>0 при Т —> оо.

В этой работе построена оценка вида

А       А                 /А       А \ А       1        /                  / А \ \ /                        / А \ \

• $г =Ч'о tE^K. ^+4,i). ^t = т Z ^?<“,)A »r -/^(«.-«to-» »г (4) к=\                           ¹ t=k*\

Здесь dia^px^ это диагональная pi^q^ матрица, по диагонали которой стоят компоненты (^xl) вектора a_t. Векторы же a_t определены для teN как последовательность (wxl) векторов, такая что ap^ = 1, если (jV) е М_р и ар^ = 0 в противном случае. Предел суммирования m рассматривается как функция Т: m = m(T).

Читатель, интересующийся только первым классом задач, может считать, что 9_Т тождественно некоторому значению 9* , не зависящему от Т .

В данной работе доказано, что оценка Z_T положительно полуопеределена для любого m, при условии, что веса w^, для этого m могут быть представлены в виде:

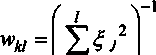
u=° у

2j^ j^ J-k’ j=k

(                                  1          )

к g (0..Z), £ J g R, V/ G (0..Z), £ £ _v² > 0

<                                 J=°         '

Будем называть данное условие на веса Wy Условием 1 .

Далее в работе доказано, что данная оценка является состоятельной оценкой ^(^*), если

• 1.    веса Wy для любых т g N,k = l...m удовлетворяют jw^j <С7 для некоторого конечного С , а также Vk : lim w^ = 1, m->oo

• 2.    т = т(Т\ такова, что lim /и(Т) = +оо и Пт m(T")T^-U4 = 0. Т ->00                  Т ->00

• 4. Теоремы о положительной полуопределённости и состоятельности

Будем называть данное условие на веса w^ Условием 2 .

К примеру, Условию 1 и Условию 2 одновременно будет удовлетворять набор весов ^=1--— (т.е. § = 1 для ус(0.../и) и w = 0,1,2...) и ^(7) = [4(7V100)2/9].

В [11] доказаны следующие две теоремы.

Теорема NW1. При выполнении Условия 1 на веса w^ матрица S_T является положительно полуопределённой.

Доказательство этой теоремы представлено в [11] и, главным образом, опирается на результат [8]. См. также [4, с. 128-132]

ТЕОРЕМА NW2. Предположим, что выполнены следующие условия:

• (i)    При любом teZ р₁(ю,0^ = ф(х_е^й),9ух₍__Л(й),0^,...х_[__т(а⁾,9^

как сложная функция Q х 0 -> R⁴ , измерима на Q при любом в g 0 и с вероятностью 1 непрерывно дифференцируема по 6 в некоторой окрестности В точки 6* - внутренней точки множества 0.

• (ii)    (а) Существует измеримая функция E(to), такая что для любого 6 g 0, для любого цело

  го t и любого to g Q верно что

  
  

  suplp, (ty.

  6еВ

  
  

  ,,5)|<Е(®) и sup -I-p_t (a,6) BeB О У

  
  

  < E(to), причём для неко

  
  

торой константы D^ > 0 верно 51 E(ty)² I <  D_H .

• (б)    Существуют числа D > 0, 5 > 0 и г > 1, такие что для любого целого / и любого / = 1 ..q

(I (Л « l⁴^"¹"^)^

верно что Е\ р; а<о,0 )      

• (iii)    Для любого 0 g 0 последовательность x_t (5) обладает свойством ф -перемешивания с коэффициентами перемешивания ф^ размера x_t^0^, либо обладает свойством хД9^- перемешивания с коэффициентами перемешивания х₍(5) размера 2г/(г-1) для некоторого г>1.

• (iv)    Случайные величины 0_Т : Q -> 0 таковы, что VT( 0_Т -0* I сходится по распределению к

некоторой случайной величине при Т -> оо .

Тогда при выполнении Условия 2 на веса w^

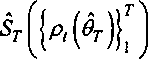
-5Г^5*)——>0 при Т->оо

В настоящей работе сравниваются обобщения теорем NW1 и NW2 для случая временных рядов различных частотностей.

Для элементов ковариационной матрицы Z_T вектора А_т в соответствии с формулами (2) и

(3) имеем

^’п=Е

^ Z ^

^ Z Р1п

1 и>‘Умр \<1<Т

i = M, j = \..q.

Пусть оценка Ег построена по формуле (4).

ТЕОРЕМА 1. При выполнении Условия 1 на веса w^ матрица Е_г является положительно по-луопределённой.

Доказательство.

Определим (9 ^х 9 случайные векторы q_t = diag^a, )p_t , но тогда

2_Г =Т₀ + ^ ^(^ +^xi^,4)> Ч^ =~ 52 ^t-k ’ ^т,е- °Ц^енка ^т ^это оценка $_т, в которой взят t=l                          ^ (=1+4

ряд qt вместо ряда pt. Из условия £(/?,) = О следует £(fz) = 0. Положительная полуопределён ность матрицы ST следует из теоремы NW1.

Теорема 1 доказана.

ТЕОРЕМА 2. Предположим, что выполнены следующие условия:

• (i)    При любом (/V) е М_р

Р^ (a),0) = Ф^(у) (х, (to,0\x_t__x (to,0y..jc_t__T (ro,0^

как сложная функция Ох0 -> R⁴, измерима на О при любом 06 0 и с вероятностью 1 непрерывно дифференцируема по 0 в некоторой окрестности В точки в* - внутренней точки 0.

• (ii)    (а) Существует измеримая функция Н(о), такая что для любого 0 е 0, для любого цело

  го t и любого ю е П верно что

  
  

supl/?, (<у,0)|<5(щ) и sup—/?, < Е(й>) , причём для некоторой веВ                  6еВ 90

константы D_H выполнено ^(Е(щ)²)<Т)_н.

(б) Существуют числа D > 0, 8 > 0 и г > 1, такие что для любого натурального t и любого

, .                      ( I со * |4(г+^)^

i = \.q таких что y,t)eM_p верно Е\ NpY’^Q )      <£>.

• (iii)    Для любого 0 е 0 последовательность х, (0) обладает свойством ф -перемешивания с коэффициентами перемешивания ф^ размера x_t (0), либо обладает свойством х, (У) -перемешивания с коэффициентами перемешивания х,^ размера 2г/(г-1) для некоторого г > 1.

• (iv)    Случайная величина 0_Т : Q -> 0 такова, что Vt ^0_т - 0* ) сходится по распределению к некоторой случайной величине при Т -><ю.

Тогда при выполнении Условия 2 на веса w^

i._T ^ Pt ^0т ) | ^“^т^*)—^-^0 при Т^оо                (7)

Доказательство теоремы 2.

Как и в доказательстве теоремы 1 определим (?х1) случайные векторы q_t -diag{a_t)p_t .

Случайные векторы pt получены из случайных векторов х, посредством измеримого преобразования pt =Ф(х, ,xt_x,...,xt_T), поэтому по теореме П5 из [3], для pt верно, что либо коэф- фициенты перемешивания ф^ имеют размер х, (У), либо коэффициенты перемешивания х, (0) имеют размер 2г/(г-1) (т.к. это верно и для xt).

Для последовательности случайных векторов g_t =diag{a_t)p_t верно что либо коэффициент перемешивания ф^ имеет размер 2r/(2r-1), либо коэффициент перемешивания x_t^ имеет размер 2r/(г-1) (т.к. это верно для p_t , а умножение на вектор, зависящий от t, - измеримое преобразование).

Заметим, что элемент ^J) может быть представлен в виде

• 1    т V 1 т         АА 1 т         * т Л А

• UiLat Pt ^Lat Pt»

z=i                   z=i                   Vx1 t=\z=i а Д в виде

„    1 т       <П    (1 т          1 г'

• 7    z StSt-k X St-k< •

Действительно,

(i) g₍(_<t)p_t^e>,9'), а р,(ю,0) = ф(х, ^to,6Yx_t__x^to,0Y---,x_t__T^(o,6y\, измерима на

Q при любом 9 g 0 и непрерывно дифференцируема по 9 при любом ® e Q в некоторой окрестности В точки 9* с вероятностью 1

(ii) т.к. для p_t ^0,9^

верно

Vaz е Q: sup|p_z (to, 0)1 < E(to),sup Д < ЭД, веВ                6еВ О 9

то и

6еВ

д

VaeQ: supk_z (<у,0)| < E(to),sup —д < E(to), где

6еВ               веВ 99

E^E(toY^H и

/ I m i4(r+5)A

Е\ |д( \to,0)|       <£> для

некоторых констант Д и Z).

• (iii ) выше доказано, что коэффициенты перемешивания для последовательности случайных векторов д имеют тот же размер, что и для последовательности x_t, то есть либо ф(к) имеет размер 2г/(2г-1), либо а(к) имеет размер 2г/(г-1).

• 5.    Заключение

Выполнение условия (iv) теоремы NW2 очевидно.

Итак, применяя теорему NW2 для последовательности случайных векторов д =diag(at)pt , А в мы имеем Ег - Sr ->0 при Т-юо .

Теорема 2 доказана.

В работе предложена оценка ковариационной матрицы для временных рядов различных частотностей и доказаны теоремы о свойствах этой оценки: положительной полуопределённости и состоятельности.

Различные результаты в математической статистике опираются на оценки ковариационной матрицы. Поэтому обладающая хорошими свойствами оценка ковариационной матрицы для рядов различных частотностей может иметь серьёзное практическое значение, расширяя применимость известных результатов на этот случай.