Оценка кризисоустойчивости предприятия со слабой динамикой с использованием нечёткой логики

ка), других способов. При этом глубже вникая и исследуя те особенности производства, из-за которых проявляется его нединамичность.

Снижение нединамичности как отдельных производств, так и предприятия в целом не только можно рассматривать как способ снижения влияния кризисной динамики на развитие предприятия, но и открыть широкие возможности для технического и технологического переоснащения предприятия.

Адекватное ранжирование предприятий по их нединамичности позволит более корректно и обоснованно разработать стратегии их антикризисной поддержки на федеральном, региональном уровнях, а также уровне предприятия. При этом существенно повысится эффективность этой поддержки за счёт учёта количественной оценки текущей степени нединамичности предприятия и имеющихся у него резервов по её снижению.

Таким образом, оценка кризисоустойчиво-сти предприятий со слабой динамикой является важной, актуальной и своевременной задаче, решение которой позволит грамотно и обоснованно применять экономические инструменты поддержки предприятия, максимально используя его собственные возможности.

МАТЕРИАЛЫ И МЕТОДЫ

Исследования влияния распределения прямых дотаций на эффективность антикризисной поддержки показали наличие ярко выраженной стохастической зависимости между данными факторами [9-13]. Поэтому для решения поставленной в работе задачи оценки кризисоустойчи-вости можно предложить два различных подхода.

Первый из них заключается в построении стохастической зависимости между кризисо-устойчивостью предприятия и степенью его нединамичности. Второй определяет формирование вместо простого ранжированного по степени нединамичности списка предприятий нечёткой лингвистической переменной для последующего анализа нечёткого отношения между кризисоустойчивостью предприятия и степенью его нединамичности.

Второй подход, по мнению автора, позволит исключить при построении нечёткой модели явное рассмотрение следующих факторов.

. Стохастичность самой задачи.

На кризисоустойчивость предприятия, скорее всего, будут в значительной степени влиять текущее состояние производственных процессов на момент наступления кризиса, объём заключённых договоров на отгрузку продукции на момент наступления кризиса, особенности реального процесса протекания кризиса, своевременность мер поддержки и противодействия кризису, качество менеджмента и т.д. Следовательно, при различных значениях упомянутых факторов, которые и определяют стохастический характер задачи, предприятие может, как успешно преодолеть кризисную динамику, так и обанкротиться в результате кризиса с определённой вероятностью. Использование нечёткой лингвистической переменной позволяет учесть данное обстоятельство: нечёткая переменная может одновременно принадлежать двум противоположным множествам. В рассматриваемой задаче – предприятий, успешно преодолевших кризис и обанкротившихся в кризис.

. Оценка точности расчёта интегрального показателя нединамичности и прогноза основных параметров кризиса.

Такая оценка является достаточно громоздкой процедурой, которая включает в себя оценку статистических и методических погрешностей математической формализации показателей, повышающих и снижающих степень недина-мичность производства, назначения весов этих показателей в показателе нединамичности про- изводства и интегральном показателе недина-мичности предприятия, вычисления параметров интеллектуального капитала предприятия и прогноза возможных эффектов от факторов, снижающих нединамичность предприятия. Задача оценки точности тоже является стохастической. Использование нечётких множеств позволяет не решать в полной мере данную задачу. Единственным требованием, определяющим точность решения, является корректность базы знаний и степень её корреляции с исходными данными: параметрами исследуемых предприятий и характеристиками моделируемого кризиса.

Сама лингвистическая переменная «Предприятия со слабой динамикой» будет иметь вид, представленный на рисунке 1. База знаний экспертной системы представляет собой блоки предикатных правил с двумя предпосылками и одной переменной выводом. Блоки собраны по каждому прошедшему кризису отдельно (рисунок 2). В качестве переменных входа используется интегральный показатель нединамичности предприятия [14] как количественная оценка степени нединамичности предприятия и численность сотрудников предприятия. Переменной выхода является вероятность успешного преодоления кризиса предприятием как количественная оценка кризисоустойчивости предприятия.

В качестве математической модели в работе предлагается реализация связи переменных входа с переменной выхода в виде нечёткого отношения, анализ которого позволяет сформировать из базы знаний с учётом базы исходных данных переменную выхода, соответствующую тем предприятиям и той кризисной ситуации, которые были формализованы в базе исходных данных.

R = (A1 x A2)^B , (1)

где R – нечёткое отношение; А₁ и А₂ – множества значений переменных входа; x - операция нечёткого прямого произведения универсальных множеств переменных входа; ^ - нечёткая импликация; В – множество значений переменной выхода.

В результате анализа нечёткого отношения (1) с помощью математической модели можно сформировать переменную выхода:

B * = ( A * x A ,* ) О R = ( A * x A ,* ) 0 ((Дх A , h B ) , (2) где В^* – сформированная переменная выхода; А₁^* и А₂^* – значения переменных входа для конкретной моделируемой ситуации; о - операция нечёткой свёртки.

В настоящей работе в качестве алгоритма формирования переменной выхода (2) используется известный и универсальный алгоритм Мамдани [15]. Затем применяется центроидный метод приведения к чёткости для количественной оценки вероятности успешного преодоления кризиса предприятием.

Предприятия со слабой динамикой

Универсальное множество

Базовое терм-множество

	Синтаксическая процедура операций с элементами базового терм-множества

Список исследуемых предприятий: 1. Предприятие 1. 2. Предприятие 2. п. Предприятие п.		Дискретная лингвистическая переменная размерности п.	—
		Нечёткие множества с конечным носителем и функциями принадлежности: 1 . S-образная. 2    Т-образная.	—
1.    Высокая степень нединамичности. 2.    Умеренная степень нединамичности. 3.    Низкая степень нединамичности.

3. Z-образная.

Связки “и”, “или”:

• 1.    Высокая и умеренная степень нединамичности.

• 2.    Умеренная или низкая степень нединамичности. Модификаторы “очень”, “не”, “критически":

• 1.    Критически высокая степень нединамичности.

• 2.    Очень низкая

• 3.    Невысокая степень

степень нединамичности.

педпнамичпостп.

Семантическая процедура создания нечётких множеств из новых значений переменной

• 1.    Связка “и” - операция пересечения нечётких множеств базового терм-множества.

• 3.    Модификатор “очень" - операция концентрации нечётких множеств базового терм-множества.

• 4.    Модификатор “не” - операция дополнения нечётких множеств базового терм-множества.

• 5.    Модификатор“критически” -операция увеличения нечёткости.

__2. Связка “или” - операция объединения нечётких множеств базового терм-множества.

Конечное число нечётких множеств с конечным носителем и различными функциями принадлежности, определяемыми В соответствие с семантической процедурой.

Рис. 1. Структура формируемой лингвистической переменной «Предприятия со слабой динамикой»

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ И РЕЗУЛЬТАТЫ

Выберем в качестве исходных данных некоторое модельное предприятие со значениями переменных входа:

П ₀ = 0,7 ± 0,2; Ч * = 500 ± 50 , (3) где п о — интегральный показатель нединамичности предприятия [14], а х * - среднегодовая численность сотрудников предприятия.

В качестве базы знаний выберем данные по кризису 2008–10 гг. предприятий Самарской области, участвовавших в мониторинге в рамках городской

антикризисной программы [16]. В общей сложности использованы данные о 38 предприятиях.

Трансформируем базу знаний в лингвистическую переменную (рисунок 3), используя базовые термы (таблица 1).

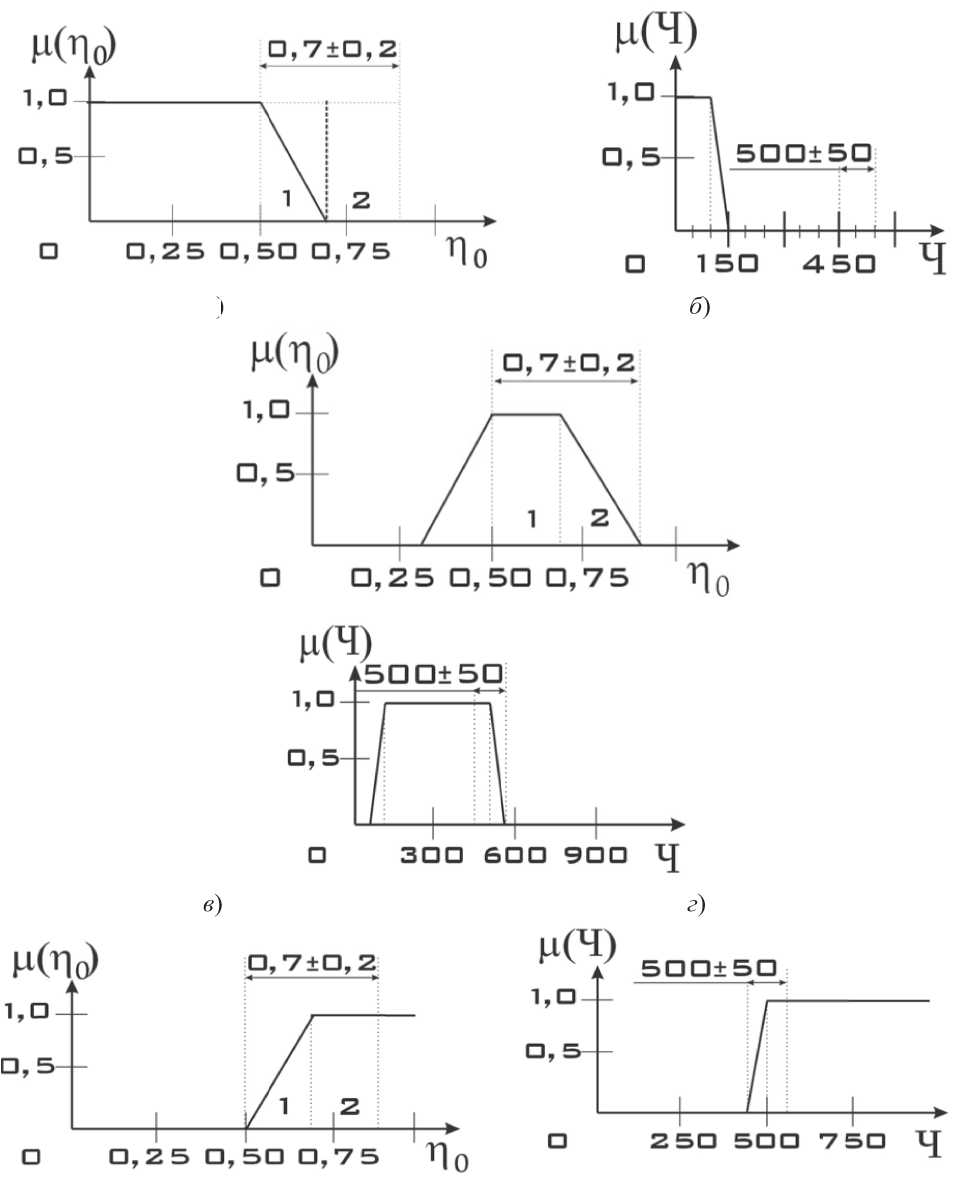
В качестве функций принадлежности нечётких подмножеств выберем линейные функции принадлежности S, T и Z классов [15] (рисунок 3). Согласно алгоритму Мамдани, применим фактические значения переменных входа (3) к их функциям принадлежности для оценки степени истинности предпосылок предикатных правил, составляющих базу знаний (рисунок 2). Результаты этой операции представлены на рисунке 4.

Рис. 2. Блок-схема базы знаний экспертной системы

Для определения чётких значения функций принадлежности переменных входа (3) используем центроидный методом, определив ординату центра тяжести функции принадлежности. На рисунке 4 а) функция принадлежности в диапазоне значений переменной входа образует две фигуры: треугольник (1 на рисунке 4 а) ), орди- 11 ната центра тяжести которого равна 3 • 1 = 3 , и прямоугольник нулевой высоты (2 на рисунке 4 а) ), ордината центра тяжести которого равна нулю. Тогда имеем:

1 + О

«1*1 — «2*1 — «3*1 — А1 (По ) — ^у ~ О’167 .

где « * - степень истинности j -й предпосылки i -го правила; А * ( п _о ) - значение функции принадлежности, полученное центроидным методом.

Аналогично для рисунков 4 б)-е) :

_ *

^— « 42

_ *

« 41

_ *

« 12

_ *

— « 51

_ *

= « 61

—    «Л — Ап (Ч ) — О>

1 + 1

—    А* (По) — -^ = о>667,

1 +1

_ * « 22

_ *

= « 52

— « * — А ( Ч ) — ^3 _s о,667,

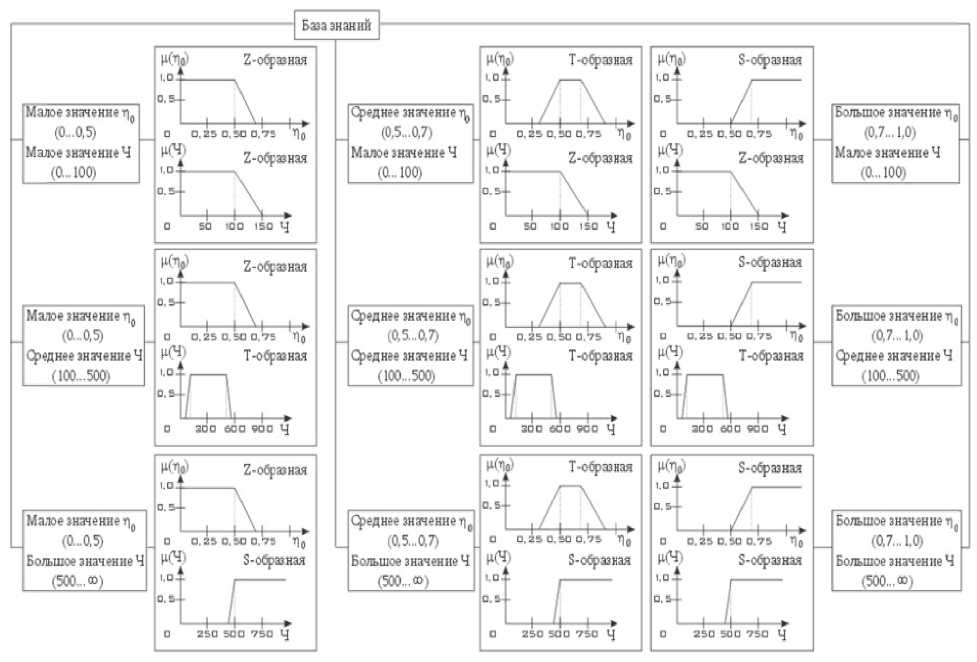
Рис. 3. Трансформация базы знаний в лингвистическую переменную

Таблица 1. Базовые термы переменных входа

Параметр	Малое значение	Среднее значение	Большое значение
п	0 –0,5	0,5 – 0,7	0,7 – 1
ч	0 – 100	100 –500	Свыше 500

a )

д )

е )

Рис. 4. Определение уровней отсечения предпосылок предикатных правил как степень соответствия фактических значений переменных входа значениям лингвистической переменной: а) малое значение п ₀ ; б) малое значение Ч ; в) среднее значение п ₀ ;

г) среднее значение Ч ; д) большое значение п ₀ ; е) большое значение Ч

Таблица 2. Статистические характеристики переменной выхода

Значение	Статистические характеристики переменной выхода
% ( x 1 ) = 0...0,5 Ч ( x 2 ) = 0...100 1] ( x 1 ) = 0...0,5	Среднее выборочное ( у ): 0,868; Выборочное CKO ( о у ): 0,095; Диапазон 1 ( у ± о у ): 0,773...0,963; Диапазон 2 ( у ± 3с у ): 0,582...1. Среднее выборочное ( у ): 0,868; Выборочное CKO ( о у ): 0,069;
Ч ( x 2 ) = 100...500 % ( x 1 ) = 0...0,5	Диапазон 1 ( у ± о у ): 0,799...0,938; Диапазон 2 ( у ± 3 о у ): 0,661...1. Среднее выборочное ( у ): 0,898; Выборочное CKO ( о у ): 0,081;
Ч ( x 2 ) = 500... ^ П ( x 1 ) = 0,5...0,7	Диапазон 1 ( у ± о у ): 0,817...0,979; Диапазон 2 ( у ± 3 о у ): 0,656...1. Нет данных в базе знаний
Ч ( x 2 ) = 0...100 П ( x 1 ) = 0,5...0,7	Среднее выборочное ( у ): 0,677; Выборочное CKO ( о у ): 0,045;
Ч ( x 2 ) = 100...500 П ( x 1 ) = 0,5...0,7	Диапазон 1 ( у ± о у ): 0,632...0,722; Диапазон 2 ( у ± 3 о у ): 0,541...0,812 Среднее выборочное ( у ): 0,810; Выборочное CKO ( о у ): 0,071;
Ч ( x 2 ) = 500... ^ П ( x ) = 0,7...1,0	Диапазон 1 ( у ± о у ): 0,739...0,881; Диапазон 2 ( у ± 3 о у ): 0,598^1. Нет данных в базе знаний
Ч ( x 2 ) = 0...100 п ( x 1 ) = 0,7...1,0	Среднее выборочное ( у ): 0,777; Выборочное CKO ( о у ): 0,100;
Ч ( x 2 ) = 100...500 п ( x 1 ) = 0,7...1,0	Диапазон 1 ( у ± о у ): 0,677...0,877; Диапазон 2 ( у ± 3 о у ): 0,476^1. Среднее выборочное ( у ): 0,706; Выборочное CKO ( о у ): 0,154;
Ч ( x 2 ) = 500... ^	Диапазон 1 ( у ± о у ): 0,552^0,860; Диапазон 2 ( у ± 3 о у ): 0,245^1.

a )

д )

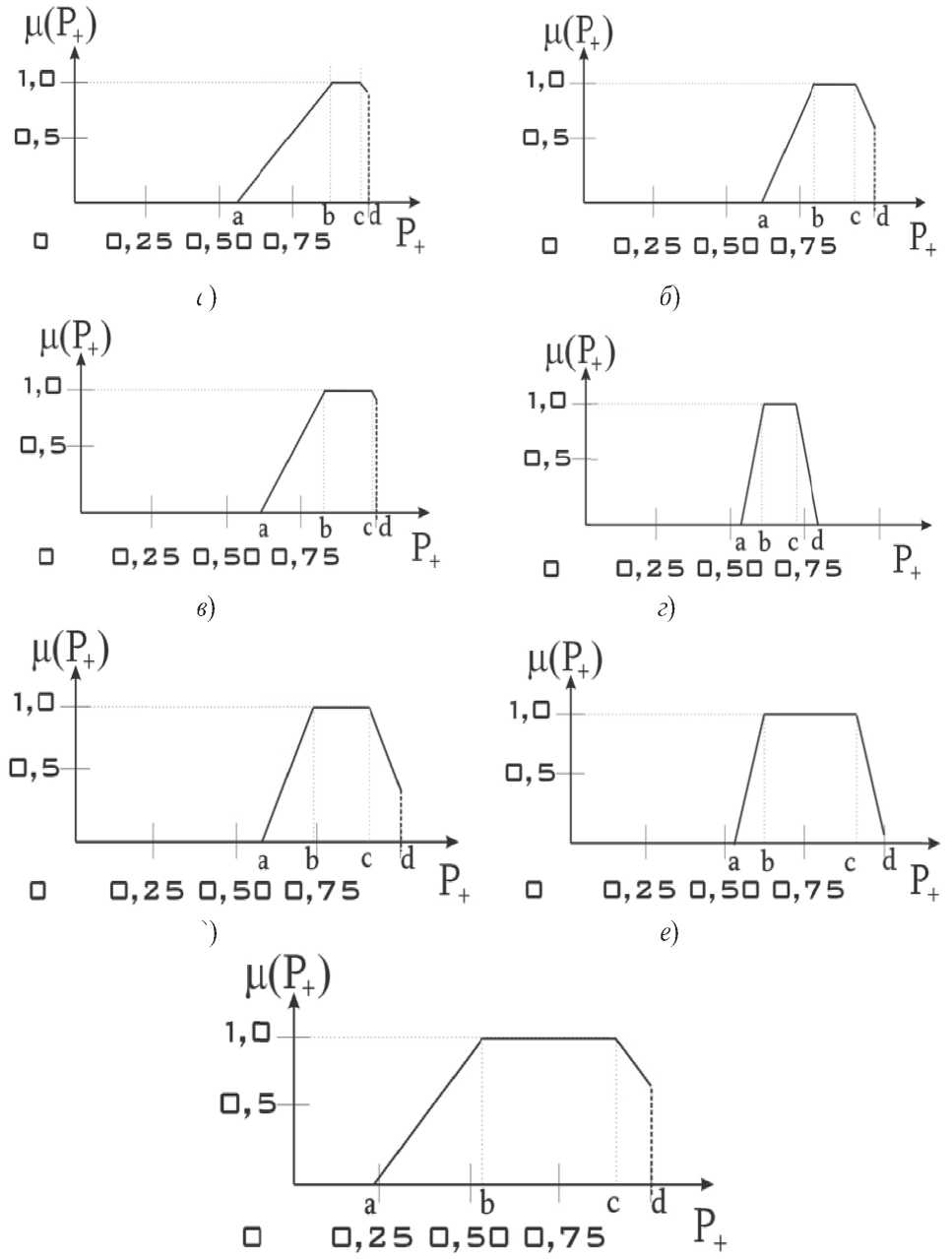
Рис. 5. Функция принадлежности переменной выхода:

а ) п 0 ( х 1 ) = 0...0,5 ; х ( х 2 ) = 0...100 ; б ) п 0 ( х 1 ) = 0...0,5 ; х ( х 2 ) = 100...500 ; в ) п 0 ( х 1 ) = 0...0,5 ; х ( х 2 ) = 500... » ; г ) п ₀ ( х 1 ) = 0,5...0,7 ; х ( х 2 ) = 100...500 ; д ) п ₀ ( х 1 ) = 0,5...0,7 ; х ( х 2 ) = 500... » ;

е ) п ₀ ( х 1 ) = 0,7...1,0 ; х ( х 2 ) = 100...500 ; ж ) п ₀ ( х 1 ) = 0,7...1,0 ; х ( х 2 ) = 500... »

U 1 ( y ) = min{a‘,	A 1 ( Р + )} = min { 0, A 1 ( Р + )} = 0 ;
U 2 " ( y ) = min { a 2 "	, A 2 ( Р + )} = min { 0,167, A 2 ( Р + )}
U 3 ( У ) = min { a *	, A 3 ( Р + )} = mm{ 0,167, A 3 ( Р + )}:
д 4 ( y ) = min { a ‘,	a. 4 ( Р + )} = min { 0, A 4 ( Р + )} = 0 ;
U 5 ( У ) = min { « ’,	A 5 ( Р + )} = m i n { 0,667, A 5 ( Р + )};
P 6 ( У ) = min { « 6 ,	A 6 ( Р + )} = m in { 0,667, A 6 ( Р + )}:
Ц 7 ( y ) = min { ^ ‘ ,	A 7 ( Р + )} = min { 0, A 7 ( Р + )} = 0 ;
A s ( y ) = min { « s ,	А з ( Р + )} = m i n { 0,667, А з ( Р + )}:
U 9 ‘ ( y ) = min { ^ ‘,	A 9 ( Р + )} = min { 0,667, A 9 ( Р + )}:

= s

' О, если Р ₊<  0,661;

7,246 P - 4,790, если 0,661 <  P <  0,684;

^ 0,167, если 0,684 <  Р ₊ <  1;

О, если Р ₊ <  0,656;

6,211 Р - 4,075, если 0,656 <  Р <  0,683;

0,167, если 0,684 <  Р ₊< 1;

= s

' 0, если Р <  0,541; ⁺

10,989 Р ₊- 5,945, если 0,541 <  Р ₊< 0,602;

0,667, если 0,602 <  Р ₊< 0,752;

• - 11,111 Р ₊ + 9,022, если 0,752 <  Р ₊< 1;

' 0, если Р, <  0,598;                            ⁽⁵⁾

+

7,092 Р ₊- 4,241, если 0,598 <  Р ₊< 0,692;

0,667, если 0,684 <  Р ₊< 0,928;

• - 7,092 Р ₊ + 7,248, если 0,928 <  Р ₊< 1;

= <

• 0, если Р ₊<  0,476;

4,975 Р ₊- 2,368, если 0,476 <  Р ₊< 0,610;

0,667, если 0,610 <  Р ₊< 0,944;

• -    5 Р ₊ + 5,385, если 0,928 <  Р ₊< 1;

0, если Р ₊<  0,245;

3,257 Р ₊ - 0,798, если 0,245 <  Р ₊< 0,450;

0,667, если 0,450 <  Р ₊< 0,962;

• -    3,257 Р ₊ + 3,801, если 0,962 <  Р ₊< 1.

Теперь можно построить интегральную функцию принадлежности переменной выхода для значений переменных входа (3), которая представляет собой, согласно алгоритму Мамдани, комбинацию из максимальных значений функций принадлежности предикатных правил (5):

ц; (у) = max {Ц (Р+), ц2 (Р+), ц3 (Р+), ц. (Р+), ц5 (Р+), ц6 (Р+), Ц (Р+), Ц (Р+), ц9 (Р+ )}=

' 0,еслиР ₊<  0,245;

= s

3,257 Р ₊ - 0,798, если 0,245 <  Р ₊<  0,450;

0,667, если 0,450 <  Р ₊<  0,962;

- 3,257Р ₊ + 3,801, если 0,962 <  Р ₊<  1.

График интегральной функции принадлежности (6) представлен на рисунке 6.

Для приведения к чёткости воспользуемся центроидным методом [15] и выражением (6):

(1P а (P )dp   ГП3,257p2 - 0,798p)dp + Г9б20,667pdp + f (- 3,257p2 + 3,801 p dp, p= 0 + - +     + = 0,245           ++     + J0,405          + +    J0,962              +              +     +

⁺      * a ( p ₊) dp₊         Г’⁴⁵°(3,257 p₊ - 0,798) dp ₊ + °’⁹⁶ 0,667 dp ₊ + ¹ ( - 3,257 p₊ + 3,801) dp,

J0<- Lx + /    +                0,245 \            +                   +      0,405               +      0,962 ^{v                +}              '    ⁺

= 0,670.

_ *

^ 71

_ *

= ^а 81

1 +1

= а* = М* (П ) = ^ - №7,

*

' 62

*

^ 32 = ® t

¹ + 1

= а„ = М (Ч )= ^у - 0,667.

Благодаря трансформации базы знаний в лингвистическую переменную, из 38 первичных предикатных правил осталось только 9, которые соответствуют значениям переменных входа, представленных на рисунке 3. Для определения уровней отсечения каждого предикатного правила, согласно алгоритму Мамдани, используем операцию минимума степеней истинности предпосылок [15]:

а * = min { а * , а ₂* } = min { 0,167; 0 } = 0;

а* ₂ = min { а * , а * } = min { 0,167; 0,667 } = 0,167;

а * = min { а ₃* , а ₂* } = min { 0,167; 0,667 } = 0,167; (4) а ₄* = min { а 1* , а ₂ } = min { 0,667; 0 } = 0;

< а * = min { а * , а ₂ } = min { 0,667; 0,667 } = 0,667; а * = min { а * , а ₂ } = min { 0,667; 0,667 } = 0,667; а * = min { а * , а ₂ } = min { 0,667; 0 } = 0;

а * = min { а * , а ₂ } = min { 0,667; 0,667 } = 0,667;

а ₉ = min { а * , а ₂ } = min { 0,667; 0,667 } = 0,667.

Построим функции принадлежности переменной выхода, используя для этого статистические характеристики предикатных правил (таблица 2).

При построении функции принадлежности будем исходить из следующих соображений:

• -    диапазон 1 (таблица 4.2) представляет собой отрезок значений переменной выхода, для которых функция принадлежности равна единице;

• -    диапазон 2 (таблица 4.2) представляет собой отрезок значений переменной выхода, для которых функция принадлежности имеет ненулевое значение;

• - используется линейная функция принадлежности Т-класса.

Полученные функции принадлежности для различных значений лингвистической переменной приведены на рисунке 5. Отрезок на рисунке 5 [b, c] соответствует диапазону 1 (таблица 2), а отрезок [a, d] - диапазону 2 (таблица 2).

Далее, согласно алгоритму Мамдани, формируем теперь функции принадлежности каждого из оставшихся девяти предикатных правил, используя функции принадлежности (рисунок 5) и значения уровней отсечения (4):

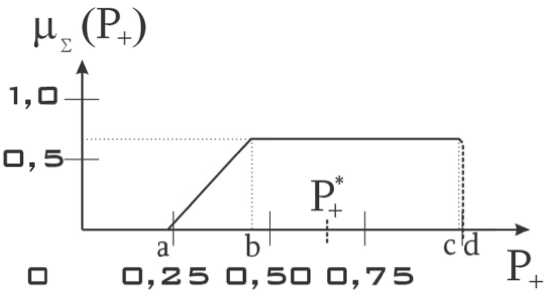
Рис. 6. Интегральная функция принадлежности переменной выхода

Таким образом, на основе имеющейся базы знаний можно оценить значение вероятности успешного преодоления кризиса предприятием, соответствующим исходным данным (3), как 67 %.

ВЫВОДЫ И ДИСКУССИЯ

Анализ полученного чёткого значения вероятности успешного преодоления кризиса предприятием зависит от конкретной решаемой задачи. Например, прямая дотационная поддержка предприятий может осуществляться при значениях вероятности успешного преодоления кризиса ниже 50 %. В этом случае данное предприятие не попадает в перечень критических. Однако рациональнее всего разработать стратегию реогранизации производств со слабой динамикой, реализуемых предприятием, с целью снижения интегрального показателя недина-мичности (3). Для достижения такой цели могут быть использованы мероприятия различных уровней:

– уровня предприятия;

– регионального уровня;

– федерального уровня.

В этом случае будет наблюдаться рост вероятности успешного преодоления кризиса.

Таким образом, по результатам проделанной работы можно сделать ряд выводов.

– Предложенный способ оценки кризисоу-стойчивости предприятия позволяет решать задачи кризисной поддержки предприятий и реорганизации производств со слабой динамикой.

– Основным преимуществом предложенного способа оценки кризисоустойчивости является отсутствие необходимости анализа стохастической постановки задачи и исследования точности переменной выхода.

– Главным недостатком можно считать зависимость результата оценки от алгоритма построения математической модели (в работе был использован алгоритм Мамдани). Однако данный недостаток не является специфическим только для аппарата нечётких множеств. При проверке статистических гипотез с использо- ванием нескольких критериев зачастую возникают ситуации, когда часть используемых критериев предлагает отвергнуть проверяемую гипотезу, а часть согласны с её принятием. По сути, это тоже нечёткость, которая устраняется в статистике она рисками совершения ошибок I-го или II-го родов.