Оценка крупномасштабных железнодорожных проектов: неосистемный подход
Автор: Кибалов Евгений Борисович, Шибикин Дмитрий Дмитриевич
Рубрика: Управление в социально-экономических системах
Статья в выпуске: 3 т.19, 2019 года.
Бесплатный доступ
Проблема оценки общественной эффективности крупномасштабных железнодорожных проектов (далее КПЖД) рассматривается в настоящей статье в свете системной парадигмы Я. Корнаи и ее инструментальной конкретизации как неосистемного подхода. В этом контексте КПЖД анализируются как большие и сложные социотехнические системы. В качестве объектов исследования выступают Ленско-Камчатская и Приполярная железнодорожные магистрали, находящиеся на стадии прединвестиционных обоснований в первом случае и частичной реализации во втором, когда неопределенность затрат и результатов чрезвычайно высока. Для оценки сравнительной эффективности названных проектов были использованы компьютерные продукты - зарубежные и отечественные, предназначенные для работы в рамках теории принятия сложных решений с полувербальными моделями и экспертной информацией. Вычислительные эксперименты показали, что разные компьютерные продукты как средства поддержки процедур принятия инвестиционных решений дают аналитикам неодинаковые рекомендации о предпочтительности сравниваемых проектов. Показано, что причина заключается в неадекватном учете в зарубежных продуктах (применительно к крупномасштабным проектам) фактора неопределенности. Делается вывод о продуктивности инструментария неосистемного подхода, реализованного авторами статьи, в качестве интегратора вербальных и математических моделей при оценке крупномасштабных проектов в ситуации неопределенности.
Крупномасштабный железнодорожный проект, системная парадигма, неосистемный подход, компьютерный продукт, ленско-камчатская магистраль, приполярная магистраль, критерии теории принятия решений
Короткий адрес: https://sciup.org/147232258
IDR: 147232258 | УДК: 330.322 | DOI: 10.14529/ctcr190310
Текст научной статьи Оценка крупномасштабных железнодорожных проектов: неосистемный подход
Проблема оценки общественной эффективности крупномасштабных железнодорожных проектов (далее КПЖД) рассматривается в настоящей статье в свете системной парадигмы Я. Кор-наи [1]. В работах Г.Б. Клейнера [2, 3] она была развита в форме новой методологии применения системного инструментария в экономических исследованиях (как теория «среднего» уровня [4]) и получила название «неосистемный подход» [2]. Наша исходная позиция состоит в анализе КПЖД как большой и сложной социотехнической системы, и поэтому термин «неосистемный подход» вынесен в название статьи, а ее содержание акцентировано на сравнении характеристик системного подхода «без» – и с приставкой «нео» на конкретном примере.
Я. Корнаи в своей парадигме предлагает построить систему оценки «великих, уникальных, неповторяющихся социальных изменений» скачкообразного типа, которую, на наш взгляд, следует назвать в соответствии с объектом оценки глобальной. Ее ключевым положением является интегративный принцип при оценке последствий подобных мегаизменений, вносимых в сложившийся внутригосударственный, а также мировой социальный порядок. Новая парадигма не сводится к какой-либо частной дисциплине, будь то экономика, социология или политология. Названные дисциплины предлагается рассматривать как комплексную «всеобъемлющую, цельную общественную науку» и особое внимание при этом уделять взаимодействию различных сфер функционирования общественной системы (не только экономики и политики, но также культуры, идеологии и истории). Это отличает парадигму Корнаи от иных системных парадигм, которые по своей сути (за исключением марксистской и ее модификаций) всего лишь междисциплинарны, а в большинстве случаев, как например методики «затраты – выгоды» и «стоимость – эффективность», опираются на постулаты экономической теории (см., например, [5, 6]).
Б.Г. Клейнер в своей трактовке неосистемного подхода также ограничивает степень глобальности системной парадигмы Корнаи уже в названии предлагаемой методологии, декларируя ее экономическое первородство и тем самым сужая общесистемный смысл парадигмы. Для оценки общественной эффективности КПЖД такое обеднение состава эффектов (прямых и косвенных), порождаемых крупномасштабными проектами, приводит к недооценке их роли как драйверов активизации экономического роста экономики и благосостояния социума. Конкретно из-за недоразвитости, например, системы железных дорог на Дальнем Востоке России падает качество жизни дальневосточников и в ситуации санкций затруднен маневр по усилению торговоэкономических связей со странами АТР. Первое ведет к обезлюдиванию суверенных территорий России, второе чревато международной изоляцией страны, а все вместе угрожает ее национальной безопасности.
Для теоретического анализа в рамках системной парадигмы Я. Корнаи не характерно использование математических моделей, в частности эконометрических. Эти модели отличаются высоким уровнем абстракции, и по необходимости работающие с ними ученые вынуждены исследовать узкий «кусок реальности» в ущерб системной полноте исследования. Напротив, сторонники системной парадигмы ради полноты готовы серьезно поступиться научной строгостью и точностью. В методологии Клейнера вопрос ставится более кардинально. Предлагается считать, что основное отличие новой системности (неосистемного подхода) от старой состоит в отказе от математической теоретико-множественной (эндогенной) основы систем и в переходе к структурной (экзогенной), в основе своей философской, теории систем.
Здесь следует подчеркнуть, что проблема соотношения теоретико-множественного и системного подхода не нова и обсуждается последние 40 лет в трудах отечественных и западных ученых. На уровне качественных определений идея множества как «многое, мыслимое как целое» состоит в том, что в ней сущность целого сводится к сущности элементов множества. В системном подходе, наоборот, «целое мыслится как многое». Конструктивный вывод как результат многолетних дискуссий, с которым авторы настоящей статьи согласны, состоит в том, что оба подхода взаимодополнительны, а системные аналитики при оценке КПЖД «обязаны владеть теоретико-множественным аппаратом во всей его строгости и математической мощи» [7, c. 72, 83].
В описании системной парадигмы Корнаи и методологии Клейнера по непонятным причинам фактор неопределенности, тотально влияющий на принятие сложных решений на всех уровнях общественного устройства современного мира, прямо не упоминается, а обсуждается, если можно так выразиться, метафорически. Относительно предсказательной силы инструментария системной парадигмы сам Корнаи отзывается скептически, т. е. ставит под сомнение его способность вскрыть неопределенности будущего. Он считает, что ожидаемый результат применения нового подхода пока не достигнут, а весьма скромные результаты «получены с большой степенью неведения», т. е. они по-прежнему неопределенны и пользоваться ими в практических приложениях следует с осторожностью.
В свою очередь Клейнер в предложенной методологии понятие неопределенности развития систем мезоуровня – объектов и проектов – вводит через понятие плохо предсказуемого взаимодействия четырех «джиннов»: вариативности, перемен, однообразия и застоя. Оставляя в стороне религиозные трактовки термина «джинн», укажем на его происхождение от арабского слова «джана» – скрытый. Действительно, будущее, образно выражаясь, скрыто от лиц (и организаций), принимающих решения, завесой неопределенности. Как эту завесу сделать более прозрачной, в методологии прямо не обсуждается, хотя делается два важных методических вывода, существенных для понимания особенностей КПЖД: а) типовой продукт (услуга) этой проектной системы – преобразование экономической системы, вмещающей проектную систему, б) эксклюзивный – нарушение гомогенности пространственно – временной среды проекта, что генерирует неопределенность при оценке эффективности проекта.
Выводы в прикладном аспекте служат ориентирами для постановки проблемы оценки крупномасштабных инвестиционных проектов на железнодорожном транспорте с учетом фактора неопределенности. Решение непростых задач, возникающих в этой связи, облегчается тем, что к настоящему времени наукой, если судить по литературе вопроса, проблема недетерминированности внутренних и внешних связей крупномасштабных и сложных систем осознана достаточно глубоко и давно (см., например, [8]). Тем не менее понимание того, что специфика объекта управления определяет специфику системы оценки эффективности таких систем, хозяйственной практикой в должной степени не достигнуто и сегодня. Крупномасштабные проекты здесь являются учебным примером, и настоящая статья написана, в частности, для того, чтобы прояснить некоторые «темные места» в описанных выше системных парадигме и методологии применительно к железнодорожному транспорту. Далее для прояснения теоретических неясностей применяется стандартный в науке прием – вычислительный эксперимент.
С этой целью при оценке двух КПЖД – Приполярной и Ленско-Камчатской железнодорожных магистралей (рис. 1), – находящихся на стадии предынвестиционных обоснований, когда неопределенность затрат и результатов чрезвычайно высока, нами были использованы компьютерные продукты – зарубежный и отечественный, предназначенные для работы в рамках теории принятия сложных решений с полувербальными моделями и экспертной информацией. Смысл вычислительных экспериментов заключался в сопоставлении предполагаемых результатов оценки названных КПЖД, полученных с помощью компьютерных продуктов, реализующих разные методологические установки: Expert Choice Т. Саати, когда многое мыслится как целое, и авторский ASPER-D, где целое мыслится как многое.
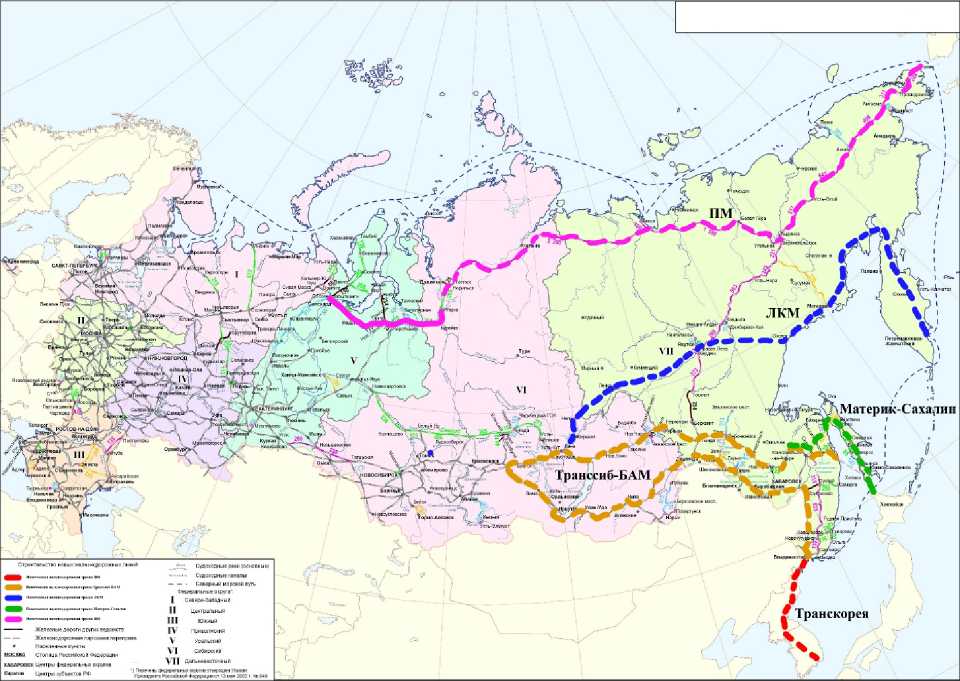
Рис. 1. Крупномасштабные железнодорожные проекты на востоке России, находящиеся в разной стадии реализации
Expert Choice – коммерческая версия известной АНР (Analityc hierarchy process) Т. Саати [9]. В работах [10, 11] указаны недостатки методики, но тем не менее она оказалась коммерчески успешной, поскольку, будучи пионерной разработкой, первой вышла на рынок систем поддержки принятия таких решений (в основном инвестиционных), когда традиционные числовые показатели экономической эффективности оказались недостаточными и должны были дополняться показателями социальной, экологической, технологической и иными видами эффективности [12].
В связи с тем, что методика Саати описана в десятках публикаций на английском и русском языках (см., например, [13, 14]), ограничимся далее схематическим представлением только ее ключевых инструментов (рис. 2). Это необходимо для сравнения с инструментарием, предложен- ным нами в разработке ASPER-D (Automatic System of Process Expert Range Dialogue – система автоматической обработки экспертных суждений в режиме диалога) для решения тех же проблем, что и Expert Choice. Но поскольку описание ASPER-D ранее не публиковалось, приведем его в нижеследующей врезке.
Методические основы ASPER-D базируются на ключевых понятиях системного анализа: дерево целей, альтернативы, экспертные оценки, система для решения проблем. Проблемы, для разрешения которых предназначен продукт, являются слабоструктурированными, т. е. значительная часть переменных и параметров, характеризующих конкретную проблему, описываются либо вербально, либо в порядковых шкалах. Количественные описания также имеют место, но они не превалируют. Методический подход, использованный в ASPER-D, вытекает из особенностей слабоструктурированных проблем, а именно:
-
1. Радикальная неопределенность проблемы. На первом этапе «вскрывается» с помощью дерева целей. Вскрытие происходит постепенно, по этапам структуризации:
-
а) в шкале классификационной – когда разрабатывается структура дерева целей;
-
б) в шкале порядковой – когда вершины дерева целей упорядочиваются по важности для достижения подцелей;
-
в) в шкале количественной – когда порядковые шкалы трансформируются в количественные с использованием коэффициентов относительной важности, нормированных к единице на каждом уровне дерева целей.
-
2. Альтернативные варианты решения проблемы. Разрабатываются экспертами как вербальные описания взаимоисключающих вариантов решения проблемы. Описание альтернатив должно быть компактным и контрастным, а число аспектов в описании альтернативы должно соответствовать числу аспектов проблемы, структурированных в дереве целей.
-
3. Сценарии развития внешней среды оцениваемых альтернатив описываются вербально как сценарии-контрасты. Минимальное число сценариев три: оптимистический, пессимистический, наиболее вероятный.
-
4. Оценочная матрица. По результатам реализации трех предыдущих этапов формируется оценочная матрица, строки которой есть оцениваемые альтернативы, а столбцы – сценарии-контрасты. Элементами матрицы являются исходы актуализации пары «альтернатива – сценарий», где численное значение исхода определяется на основе экспертных суждений.
-
5. Правила выбора наиболее предпочтительных альтернатив. Предпочтительные альтернативы выбираются по оценочной матрице на основании критериев: Вальда, Сэвиджа, максимакса, Гурвица, обобщенного критерия Гурвица – в случаях радикальной неопределенности и Байеса – Лапласа – для случаев неопределенности вероятностной.
-
6. Проверка согласованности экспертных суждений. Осуществляется по каждой оценочной процедуре с помощью коэффициента конкордации сравниваемого с табличной нормой, при заданном уровне альфа.
Отметим, что в сравниваемых методиках на этапе целевой структуризации сложной проблемы комплексной оценки проектов в основу положена одна и та же математическая структура – иерархия. Такой подход означает, что системный анализ начинается с целей и критериев их достижения, обеспечиваемого разными проектами в разной степени. И дело не только (и не столько) в том, что в обеих методиках с помощью одной и той же математической структуры строится полуформальная модель системы целей, именуемая деревом целей. Суть в том, что на первоначальных исходных стадиях осуществления проекта во главу угла ставится и с помощью дерева целей по возможности решается задача «вскрытия» так называемой целевой неопределенности, порождаемой нестабильностью внешней среды проекта, неоднородностью критериев оценки и некомпетентностью лиц (или организаций), проект инициирующих. Последнее преодолевается на основе экспертных и компьютерных технологий, оцифровывающих экспертные суждения и дающих возможность использовать компьютеры как усилители интеллекта аналитиков и лиц, принимающих решения.
Чтобы продемонстрировать не только общность двух сравниваемых далее методик, но и неодинаковость подходов к построению оценочной системы «дерево целей – проекты», обратимся к рис. 2 и 3.
Уровни иерархии
Общее благосостояние страны
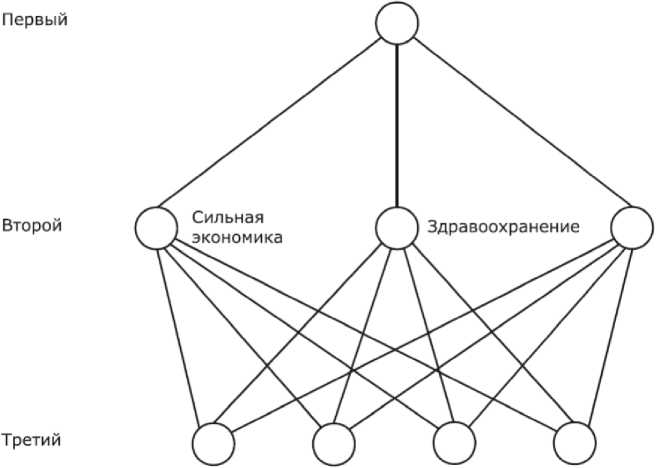
Национальная оборона
Отрасли промышленности
Рис. 2. Схема решения проблемы оценки в Expert Choice
Чтобы продемонстрировать, как это делается в ASPER-D, и на конкретном примере сравнить результаты, полученные по указанным методикам при оценке одних и тех же проектов, обратимся сначала к рис. 1. Изображенные на нем КПЖД – Приполярная и Ленско-Камчатская магистрали – являются объектами оценки их сравнительной эффективности, а полученные с помощью программных продуктов ASPER-D и Expert Choice результаты далее комментируются.
Начнем с демонстрации дерева целей в ASPER-D (см. рис. 3) как основы целевой структуризации процедур оценки, формирования системы оценочных критериев и многомерной функции ценности сравниваемых проектов. Дерево целей строится экспертами в назывной шкале в процессе «мозгового штурма» и соответствующая информация вводится для дальнейшей обработки. Система процедур ASPER-D на основе экспертных оценок выявляет наиболее предпочтительную альтернативу из числа оцениваемых: в нашем случае это КПЖД – Приполярная или Ленско-Камчатская магистраль.
Для разъяснения процедур ASPER-D в смысле их отличия от процедур Expert Choice подчеркнем, что сначала в ASPER-D оценивается не вектор коэффициентов относительной важности (КОВ) целей, а матрица отношений этих коэффициентов.
Пусть T 1 , . „, T n - цели критериального среза. Допустим, что p = ( p 1 , . „, p n ) > 0 - вектор «истинных» искомых коэффициентов (неизвестный нам). Тогда оцениваемая матрица отношений имеет вид S ( p ) = ( s iy ( p )) П , где S y ( p ) = Pi/P y • Очевидны следующие ее свойства:
s ii ( p ) = p i( p i = 1 (на диагонали стоят единицы); (1)
-
s iy ( p ) ■ S yi ( p ) = ( p i/ p y ) ■ ( p y / p i ) = 1 (симметричные элементы взаимно обратны); (2)
-
s ty ( p ) ■ s yk ( p ) = ( p t ( P j ) ■ ( p y /Pk ) = pi ( Pk = s tk ( p )• (3)
0. Генеральная цель: создание системы железных дорог, решающей проблему "транспортной недостаточности" восточного макрорегиона России
Матрица состоятельна , если она обладает первыми двумя свойствами, и сверхтранзитивна , если для нее выполнено свойство (3). Легко проверить, что первые два свойства следуют из третьего, всякая сверхтранзитивная матрица состоятельна.
Теперь рассмотрим некоторые варианты формирования матрицы S , помятуя, что ее элемент si j – это исходная оценка отношения коэффициентов относительной важности целей Ti и T j на основании экспертной информации.


0.3. Обеспечение хозяйственного освоения прибрежных территорий Дальнего Востока и ресурсного потенциала Камчатки
0.1. Обеспечение хозяйственного освоения территорий Российской Арктики и районов Крайнего Севера
0.2. Обеспечение национальной безопасности России в арктическом и дальневосточном секторах восточного макрорегиона
Коэффициенты относительной важности (КОВ)
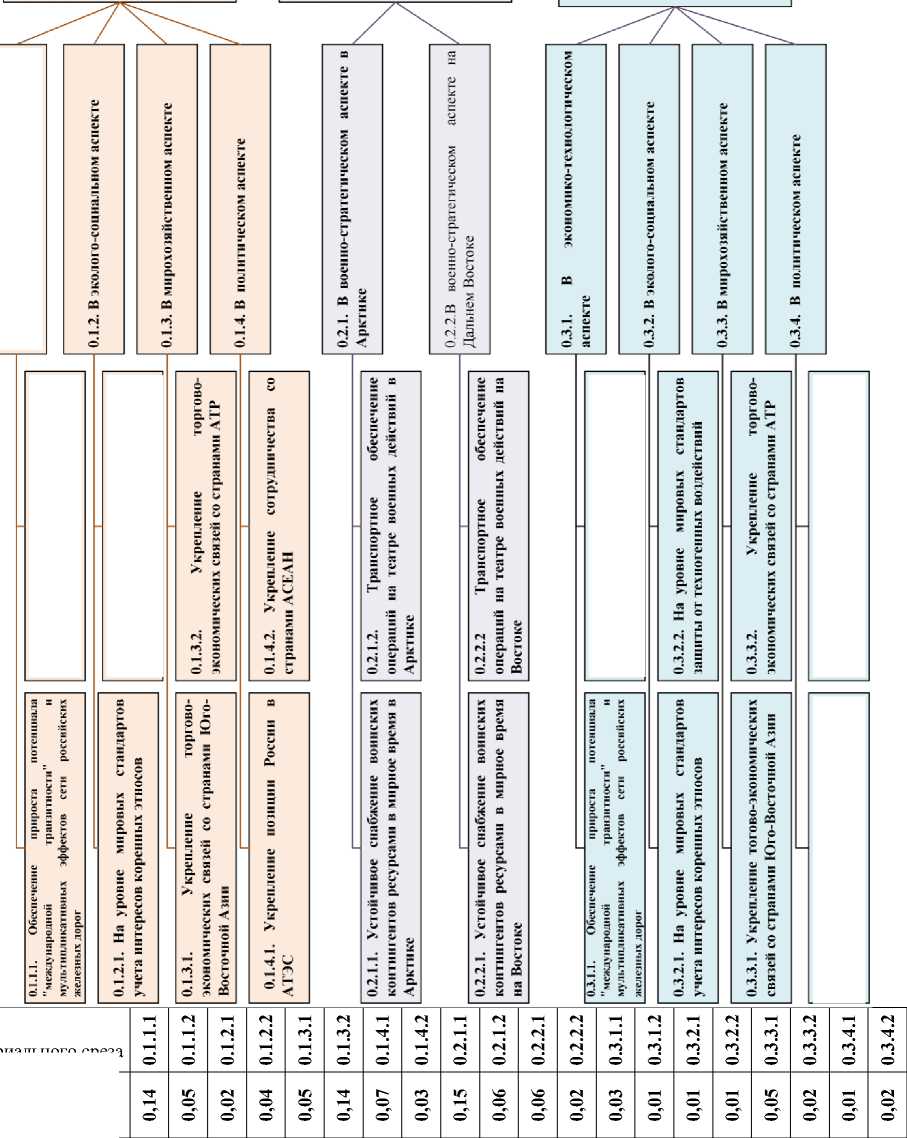
Рис. 3. Система целей КПЖД (после квантификации)
|
© |
|
|
3 © © |
|
|
© я |
|
|
© |
|
|
as |
|
|
о |
те |
|
X |
S |
|
|
те |
© |
|
|
X в «5 = X X а» = = |
X с J 5 й S S 3 Z |
о 1 |
|
о |
1 |
|
X |
|
|
н а те з я S = 5 £ « з 5 В О О В в в I £ П ^ h те и Я » |
|
|
В В |
|
|
= 5 |
|
™ !■ |
|
X X |
|
<е те в |
|
-3 |
|
- L. О |
|
- 2 х |
|
х ч g g И X |
|
£ =! |
|
3 5 = |
|
5 * % |
|
■ 6 8 |
|
U в с |
|
3 X |
|
ri 5 5 |
|
— X - |
|
П те © |
|
о а х |
|
5 х IS |
|
> |
|
|
5 и |
|
Коды критериального среза
Т.Л. Саати предложил попарно сравнивать цели критериального среза, сопоставляя каждой паре ( Ti , Tj ) оценку в соответствии с табл. 1.
Понятно, что пара ( Ti , Ti ) получит оценку 1, и достаточно сравнить n ( n – 1)/2 пар ( Ti , Tj ) для i < j . «Чувствительный» эксперт может использовать промежуточные значения оценок. Если экспертов несколько, то выставленные ими оценки усредняются. Результирующие оценки и образуют матрицу S . Если эксперт один, то матрица S состоятельна, в противном случае состоятельность не гарантирована.
Таблица 1
Шкала относительной значимости
|
Соотношение значимости целей |
Количественная оценка |
|
Равная важность |
1 |
|
T i умеренно превосходит T j |
3 |
|
Ti сильно превосходит T j |
5 |
|
T j умеренно превосходит T i |
1/3 |
|
T j сильно превосходит T i |
1/5 |
В ASPER-D использован подход к формированию исходной матрицы S , предложенный А.Б. Хуторецким [15] и устраняющий произвол выбора количественных оценок соотношения значимости целей в методе Т. Саати. В соответствии с этим подходом каждому эксперту предлагают упорядочитьвсе сравниваемые цели по неубыванию значимости (вклада в достижение генеральной цели). Упорядочение имеет очевидные достоинства по сравнению с попарными сравнениями: экспертиза проходит быстрее; эксперт лучше выявляет свои предпочтения, обозревая цели в совокупности; гарантирована транзитивность результата экспертизы. Экспертизу, в которой участвуют m экспертов, можно интерпретировать как « турнир » между сравниваемыми целями. В этом турнире сравнение целей Ti и T j одним экспертом является «партией» между ними: цель, которую эксперт считает более важной, «выигрывает» очко, если же цели равнозначимы по мнению эксперта, то каждая получает половину очка. Таким образом, между любыми двумя целями T i и T j происходит «локальный турнир» из m партий; пусть a ij – число очков, присвоенных в этом турнире цели T i (цель T i «набрала» a ij очков, играя против T j ). Конечно, любая цель «против себя» получает половину очка в каждой партии, поэтому a ii = m /2. Отношение величин a ij и a ji является естественной исходной оценкой относительной значимости целей T i и T j .
Заметим, что сформировать матрицу S , полагая s ij = a ij / a j i , мы можем, только если все a ij не равны нулю (нет такой пары целей, в отношении которой мнения всех экспертов совпадают). Тем не менее такая ситуация возможна и ее вероятность растет с ростом квалификации экспертов. Поэтому, если среди a ij есть нули, введем «нейтрального» эксперта, для которого все цели равноценны. Это увеличит все a ij на 0,5 и снимет проблему. Итак, s ij = a ij / a ji , если a ij ≠ 0 для всех i и j , иначе s ij = ( a ij + 0,5)/( a ji + 0,5).
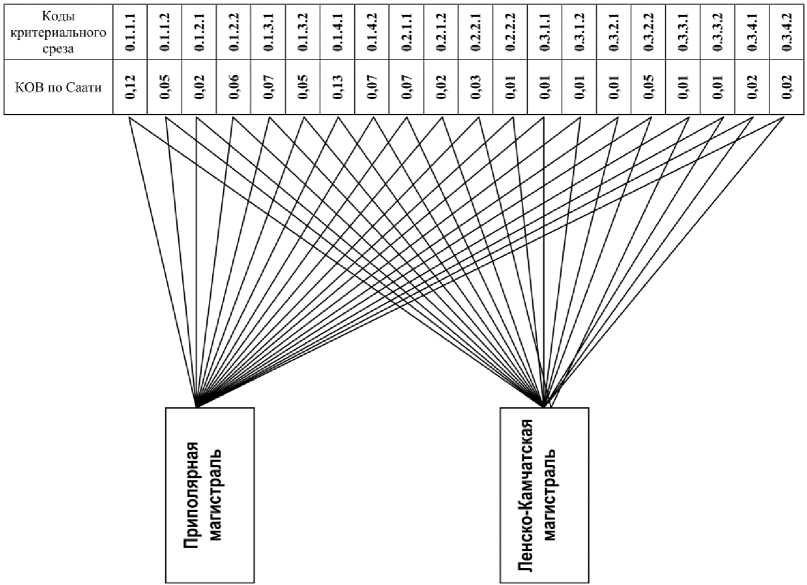
Итак, в столбце «КОВ EC » табл. 2 (числовая конкретизация матрицы S) указаны полученные с помощью продукта Expert Choice коэффициенты относительной важности подцелей критериального среза дерева целей, изображенного на рис. 3, а в столбце «КОВ AD » – те же коэффициенты, полученные с помощью программного продукта ASPER-D.
Действуя далее по методике Саати (см. рис. 2), т. е. при базовом (определенном) сценарии, получаем следующий результат (рис. 4 и табл. 3).
Начнем со сценариев-контрастов (табл. 4). Подчеркнем, что в методологии системного анализа сценарии не предназначаются для прогнозирования (предсказания) будущего; они дают лишь преимущественно качественное описание возможных состояний неопределенного будущего, если и когда оно меняется радикально. В нашем случае объектом сценирования служит внешняя среда КИП – экономика России в целом, представляемая как многослойная система, где нижним слоем является Восточный регион, о «транспортной недостаточности» которого речь шла выше. Как возможные трансформации модели состояния экономики и общества России в перспективе до 2035 г. были описаны три сценария-контраста (см. табл. 4).
Таблица 2
|
Критерии |
0,14 |
0,05 |
0,02 |
0,04 |
0,05 |
0,14 |
0,07 |
0,03 |
0,15 |
0,06 |
0,06 |
0,02 |
0,03 |
0,01 |
0,01 |
0,01 |
0,05 |
0,02 |
0,01 |
0,02 |
Ср. геом. |
КОВ EC* |
КОВ AD** |
|
0.1.1.1 |
1 |
5 |
7 |
5 |
5 |
1 |
7 |
9 |
1 |
5 |
5 |
7 |
9 |
9 |
9 |
9 |
5 |
7 |
9 |
7 |
6,10 |
0,12 |
0,14 |
|
0.1.1.2 |
0,20 |
1 |
3 |
3 |
1 |
0,14 |
0,33 |
3 |
0,20 |
1,00 |
1,00 |
3 |
3 |
5 |
5 |
5 |
1 |
3 |
5 |
5 |
2,44 |
0,05 |
0,05 |
|
0.1.2.1 |
0,14 |
0,33 |
1 |
0,20 |
0,14 |
0,11 |
0,20 |
0,20 |
0,11 |
0,20 |
0,20 |
1 |
0,33 |
3 |
3 |
3 |
0,33 |
1 |
3 |
1 |
0,93 |
0,02 |
0,02 |
|
0.1.2.2 |
0,20 |
0,33 |
5 |
1 |
1,00 |
0,14 |
0,33 |
5 |
0,14 |
0,33 |
0,33 |
5 |
5 |
7 |
7 |
7 |
1,00 |
5 |
7 |
5 |
3,14 |
0,06 |
0,04 |
|
0.1.3.1 |
0,20 |
1 |
7 |
1 |
1 |
0,14 |
1,00 |
5 |
0,11 |
1,00 |
0,20 |
7 |
3 |
7 |
7 |
7 |
1 |
7 |
7 |
7 |
3,53 |
0,07 |
0,05 |
|
0.1.3.2 |
1,00 |
7 |
9 |
7 |
7 |
1 |
3 |
9 |
1 |
5 |
5 |
7 |
7 |
9 |
9 |
9 |
5 |
7 |
9 |
7 |
6,20 |
0,12 |
0,14 |
|
0.1.4.1 |
0,14 |
3 |
5 |
3 |
3 |
0,33 |
1 |
5 |
0,14 |
3 |
3 |
5 |
5 |
5 |
5 |
5 |
3 |
5 |
5 |
5 |
3,48 |
0,07 |
0,07 |
|
0.1.4.2 |
0,11 |
0,33 |
5 |
0,20 |
0,2 |
0,11 |
0,20 |
1 |
0,11 |
0,20 |
0,20 |
5 |
1 |
7 |
7 |
7 |
0,33 |
5 |
7 |
5 |
2,60 |
0,05 |
0,03 |
|
0.2.1.1 |
1,00 |
5 |
9 |
7 |
5 |
1,00 |
7 |
9 |
1 |
5 |
5 |
9 |
7 |
9 |
9 |
9 |
5 |
9 |
9 |
9 |
6,50 |
0,13 |
0,15 |
|
0.2.1.2 |
0,20 |
1 |
5 |
3 |
1 |
0,20 |
0,33 |
5 |
0,20 |
1 |
1 |
5 |
5 |
7 |
7 |
7 |
1 |
5 |
7 |
5 |
3,35 |
0,07 |
0,06 |
|
0.2.2.1 |
0,20 |
1 |
5 |
3 |
1 |
0,20 |
0,33 |
5 |
0,20 |
1,00 |
1 |
5 |
5 |
7 |
7 |
7 |
1 |
5 |
7 |
5 |
3,35 |
0,07 |
0,06 |
|
0.2.2.2 |
0,14 |
0,33 |
1 |
0,20 |
0,14 |
0,14 |
0,20 |
0,20 |
0,11 |
0,20 |
0,20 |
1 |
0,33 |
3 |
3 |
3 |
0,33 |
1 |
3 |
1 |
0,93 |
0,02 |
0,02 |
|
0.3.1.1 |
0,11 |
0,33 |
3 |
0,2 |
0,33 |
0,14 |
0,20 |
1,00 |
0,14 |
0,20 |
0,20 |
3 |
1 |
5 |
5 |
5 |
0,33 |
3 |
5 |
1 |
1,71 |
0,03 |
0,03 |
|
0.3.1.2 |
0,11 |
0,2 |
0,33 |
0,14 |
0,14 |
0,11 |
0,20 |
0,14 |
0,11 |
0,14 |
0,14 |
0,33 |
0,20 |
1 |
1 |
1 |
0,20 |
1,00 |
1 |
0,33 |
0,39 |
0,01 |
0,01 |
|
0.3.2.1 |
0,11 |
0,2 |
0,33 |
0,14 |
0,14 |
0,11 |
0,20 |
0,14 |
0,11 |
0,14 |
0,14 |
0,33 |
0,20 |
1,00 |
1 |
1 |
0,20 |
1,00 |
1 |
0,33 |
0,39 |
0,01 |
0,01 |
|
0.3.2.2 |
0,11 |
0,2 |
0,33 |
0,14 |
0,14 |
0,11 |
0,20 |
0,14 |
0,11 |
0,14 |
0,14 |
0,33 |
0,20 |
1,00 |
1,00 |
1 |
0,20 |
1,00 |
1 |
0,33 |
0,39 |
0,01 |
0,01 |
|
0.3.3.1 |
0,20 |
1 |
3 |
1 |
1 |
0,20 |
0,33 |
3 |
0,20 |
1,00 |
1,00 |
3 |
3 |
5 |
5 |
5 |
1 |
3 |
5 |
3 |
2,25 |
0,05 |
0,05 |
|
0.3.3.2 |
0,14 |
0,33 |
1,00 |
0,20 |
0,14 |
0,14 |
0,20 |
0,20 |
0,11 |
0,20 |
0,20 |
1,00 |
0,33 |
1 |
1 |
1 |
0,33 |
1 |
3 |
1 |
0,63 |
0,01 |
0,02 |
|
0.3.4.1 |
0,11 |
0,2 |
0,33 |
0,14 |
0,14 |
0,11 |
0,20 |
0,14 |
0,11 |
0,14 |
0,14 |
0,33 |
0,20 |
1,00 |
1,00 |
1,00 |
0,20 |
0,33 |
1 |
0,33 |
0,36 |
0,01 |
0,01 |
|
0.3.4.2 |
0,14 |
0,20 |
1 |
0,20 |
0,14 |
0,14 |
0,20 |
0,20 |
0,11 |
0,20 |
0,20 |
1,00 |
1,00 |
3 |
3 |
3 |
0,33 |
1,00 |
3 |
1 |
0,95 |
0,02 |
0,02 |
|
49,62 |
1,00 |
1,00 |
|||||||||||||||||||||
Оценка эффективности ПМ и ЛКМ по Саати
* КОВ по Expert Choice;
** КОВ по ASPER-D.
КПЖД 1
КПЖД 2
Рис. 4. КОВ критериального среза по Саати и схема оценки при базовом сценарии
Оценочная матрица по Саати
Таблица 3
|
Альтернатива |
Базовый сценарий |
|
ЛКМ |
0,176 |
|
ПМ |
0,824 |
Таблица 4
Сценарии-контрасты
|
1. Модель экономики и общества России в интервале 2020–2035 гг. |
||
|
1.1. Рыночная экономика с сильным государственным регулированием и ориентацией в своем развитии на Восточный вектор |
1.2. Экономика при ситуационном государственном регулировании и многовекторной ориентацией в своем развитии |
1.3. Рыночная экономика при слабом государственном регулировании и ориентацией в своем развитии на Западный вектор |
Список литературы Оценка крупномасштабных железнодорожных проектов: неосистемный подход
- Корнаи, Я. Системная парадигма / Я. Корнаи // Вопросы экономики. - 2002. - № 4. - С. 4-22.
- Клейнер, Г.Б. Системная парадигма в экономических исследованиях: новый подход / Г.Б. Клейнер. - http://kleiner.ru/wp-content/uploads/2014/12/Sistemnaya-paradigma-v-e'konomicheskih-issledovaniyah.pdf (дата обращения: 09.01.2019).
- Клейнер, Г.Б. Эволюция институциональных систем / Г.Б. Клейнер. - М.: Наука, 2004. - 240 с.
- Merton, Robert K. On Sociological Theories of the middle range / Robert K. Merton // On Theoretical Sociology. Five Essays. Old and New. -N.-I: Free Press; L.: Macmillan, 1967.
- Квейд, Э. Анализ сложных систем / Э. Квейд; пер. с англ. под ред. И.И. Ануреева, И.М. Верещагина. - М.: Советское радио, 1969. - 520 с.
- Хитч, Чарлз Дж. Военная экономика в ядерный век: пер. с англ. / Чарльз Хитч, Роланд Маккин; под ред. и с предисл. [с. 5-25] канд. экон. наук полк. А.А. Корниенко и канд. ист. наук кап. 1 ранга В.М. Кулакова. - М.: Воениздат, 1964. - 624 с.
- Шнейдер, Ю.А. Теория множеств и теория систем / Ю.А. Шнейдер // Системные исследования. Ежегодник 1978. - С. 70-85.
- Петраков, Н.Я. Фактор неопределенности и управление экономическими системами / Н.Я. Петраков, В.И. Ротарь; отв. ред. докт. физ.-мат. наук С.А. Айвазян. - М.: Наука, 1985. - 191 с.
- Saaty T.L. The analytic hierarchy process. - N.-Y.: McGraw Hill, 1980. - 288 p.
- DOI: 10.21236/ADA214804
- http://www.gorskiy.ru/Articles/Dmss/AHP.html (дата обращения: 21. 02. 2019).
- Подиновский, В.В. О некорректности метода анализа иерархий / В.В. Подиновский, О.В. Подиновская // Проблемы управления. - 2011. - № 1. - С. 8-13.
- Boyle, H.F. Investment Analysis: US Oil and Gas Producers Score High in University Survey / H.F. Boyle, G.K. Sehenck // Hydrocarbon Economics and Evaluation Symposium, Dallas, 14-15 March, 1985.
- Saaty, T. Decision making with the analytic hierarchy process / T. Saaty // International journal of services sciences. - 2008. - Vol. 1. - P. 83-98.
- DOI: 10.1504/IJSSCI.2008.017590
- Саати, Т. Принятие решений. Метод анализа иерархий: пер. с англ. / Т. Саати. - М.: Радио и связь, 1993. - 320 с.
- Хуторецкий, А.Б. Экспертное оценивание объектов по неквантифицируемому критерию с помощью модели Бержа - Брука - Буркова: препринт / А.Б. Хуторецкий. - Новосибирск: ИЭ и ОПП СО РАН, 1994. - 15 с.


