Оценка межрегионального неравенства в Российской Федерации по индексу социального благополучия населения

Автор: Бобков В.Н., Губарев Р.В., Дзюба Е.И., Файзуллин Ф.С.

Журнал: Экономические и социальные перемены: факты, тенденции, прогноз @volnc-esc

Статья в выпуске: 5 т.17, 2024 года.

Бесплатный доступ

В рамках исследования была поставлена цель разработки адекватного (высокоточного) инструментария, позволяющего проводить не только ретроспективную, но и перспективную оценку межрегионального неравенства по уровню жизни в Российской Федерации, исходя из индекса социального благополучия населения, являющегося результатом свертки частных индексов. Сначала выдвигается гипотеза о возможности построения адекватной прогностической (традиционной эконометрической) модели зависимости среднедушевых денежных доходов населения от группы факторов. Информационной базой исследования послужили официальные данные региональной статистики за 2015-2022 годы. В ходе эмпирического исследования (корреляционно-регрессионного анализа) были разработаны три эконометрические модели, различающиеся количеством факторов (от 2 до 4). Они позволяют (согласно средней ошибке аппроксимации, принимающей значения из интервала от 8,8 до 9,6% для разных эконометрических моделей) лишь с приемлемой степенью точности аппроксимировать данные региональной статистики. Далее проверялась аналогичная гипотеза, но предполагающая применение другого инструментария (индексный метод в сочетании с искусственным интеллектом), позволяющего измерять зависимость уровня жизни населения от группы факторов. В ходе нейромоделирования было установлено, что любая из пяти искусственных нейронных сетей, включенных в байесовский ансамбль, позволяла аппроксимировать данные региональной статистики с высокой степенью точности (со средней ошибкой от 2,8 до 3,9%). Таким образом, вторую гипотезу можно считать подтвержденной. В рамках исследования прогностическая функция была реализована путем формирования байесовского ансамбля искусственных нейронных сетей. Полученные результаты эмпирического исследования могут выступить в качестве научной базы при корректировке (актуализации) социально-экономической политики регулирования уровня жизни населения и его межрегионального неравенства среди субъектов РФ.

Еще

Регионы России, межрегиональное неравенство, уровень жизни, денежные доходы, индексный метод, корреляционно-регрессионный анализ, искусственный интеллект, прогнозирование

Короткий адрес: https://sciup.org/147245928

IDR: 147245928 | DOI: 10.15838/esc.2024.5.95.3

Текст научной статьи Оценка межрегионального неравенства в Российской Федерации по индексу социального благополучия населения

В настоящее время Россия принимает активное участие в реализации международной программы ООН «Цели устойчивого развития». Десятой целью является сглаживание социального неравенства. Различают несколько видов социального неравенства. В рамках данного исследования ограничимся изучением монетарного (доходного) неравенства.

Опираясь на статистические данные, кратко охарактеризуем его уровень в современной России. Так, например, значение коэффициента фондов принимало практически идентичное значение порядка (14) и в 2000, и в 2022 году. В 2023 году соотношение денежных доходов 10% наиболее и 10% наименее обеспеченного населения страны составляло 14,8 и было несколько ниже, чем в 2015 году (15,5). Однако и в настоящее время (2023 год) в отдельных регионах России значение коэффициента фондов значительно превышает среднероссийское. Так, в частности, в Ненецком автономном округе зна- чение показателя составляет 19,3, в Республике Адыгее – 15,5, Краснодарском крае – 15,7, Тюменской области с АО – 19,2 (из-за аномально высокого значения коэффициента фондов в Ямало-Ненецком автономном округе – 22,8), Республике Саха (Якутии) – 16,1, Магаданской и Сахалинской областях – 15,5 / 15,6 и, наконец, в Чукотском автономном округе – 17,3.

Значение децильного коэффициента в 2015–2019 гг. и 2021 году в России составляло порядка 7–7,2. В 2022 и 2023 гг. соотношение минимальных доходов 10% наиболее обеспеченного и максимальных доходов 10% наименее обеспеченного населения России принимало более низкие значения, 6,6 и 6,8 соответственно. Однако и в настоящее время (2023 году) в отдельных регионах (их список практически идентичен вышеприведенному) значение децильного коэффициента, как и коэффициента фондов, было значительно больше, чем в среднем по стране.

О высокой степени поляризованности российского общества по денежным доходам на современном этапе развития страны свидетельствует и ряд других показателей. Так, например, если в 2023 году среднедушевые денежные доходы граждан из первой группы (5,5%) составляли 14564 руб., то граждан из пятой группы (46,4% от общей величины денежных доходов) – 123349 руб., т. е. были выше практически в 8,5 раза. При этом необходимо отметить очень высокую степень концентрации населения с наибольшими денежными доходами (5-я группа) в столице. Так, порядка 43,3% от общероссийского значения показателя приходилось на г. Москву, а с учетом г. Санкт-Петербурга превышало отметку в 50%.

Таким образом, можно сделать вывод, что в современной России важным направлением государственной социальной политики выступает сглаживание межрегионального монетарного неравенства. Развитие такого направления в условиях ряда негативных внешних факторов, в частности санкционного давления на национальную экономику со стороны США и стран Европейского союза, предполагает наличие адекватного инструментария для мониторинга ситуации.

В связи с этим целью данного исследования является оценка межрегионального неравенства в Российской Федерации по индексу социального благополучия населения с применением искусственного интеллекта. Такой адекватный (высокоточный) метод экономикоматематического моделирования позволяет проводить не только ретроспективную, но и перспективную оценку изучаемого явления. Для достижения поставленной цели были решены следующие задачи:

– проведен анализ межрегионального неравенства по уровню жизни населения;

– разработан методический инструментарий оценки межрегионального неравенства по индексу социального благополучия;

– выполнена группировка регионов по индексу социального благополучия, сформирован прогноз.

Объектом данного исследования являются субъекты Российской Федерации. Предмет исследования – измерение уровня жизни их населения.

Достижение поставленной цели и решение задач предопределили структуру работы: вначале уточняется понятийный аппарат, затем проводится тематическое эмпирическое исследование.

Обзор литературы

Сложность дефиниций «качество и уровень жизни населения» привела к появлению множества различных их трактовок, небезуспешная попытка классификации (систематизации) которых предпринята в работе (Спиридонов, Найденова, 2024). Так, по мнению авторов вышеуказанной научной статьи, через призму категорий «потребности», «интересы» и «ценности» все многообразие трактовок можно объединить в три подхода: 1) базовый подход, учитывающий потребности (П-подход); 2) аксиологический подход, учитывающий ценности (Ц-подход); 3) синтез первых двух подходов (ПЦ-подход). Авторы данного исследования в части трактовки дефиниций «качество и уровень жизни населения» придерживаются базового подхода (основанного на потребностях). В свою очередь, удовлетворение потребностей населения предполагает наличие различных источников денежных доходов (включая заработную плату).

В рамках анализа эффективности деятельности органов исполнительной власти на мезоуровне управления монетарное неравенство населения России оценивается через темпы роста реальных денежных доходов населения и реальной среднемесячной заработной платы1. Это позволяет задействовать управленческий фактор в регулировании социально-экономических неравенств в нашей стране (Мерзляков, Богданов, 2022). Однако данные показатели через динамику сопоставимых цен учитывают изменение душевых доходов и заработной платы только внутри регионов. Если их применять для измерения межрегионального неравенства, то его уровень не будет отражать межрегиональные различия в уровне жизни населения, поскольку не учитывает разную покупательную способность населения в российских регионах.

О важности учета различий в покупательной способности населения для обеспечения корректности проводимых межрегиональных сравнений свидетельствует ряд тематических работ (Бобков, Одинцова, 2020, с. 179–182; Суринов, Луппов, 2022; Бобков, Гулюгина, 2023).

Согласно авторскому определению, покупательная способность населения по доходам и заработной плате представляет собой количество наборов прожиточного минимума / потребительских корзин (в среднем на душу населения, трудоспособного населения), приходящихся на заданный размер душевых денежных доходов, заработной платы. Этот показатель измеряет уровень жизни населения, т. е. текущее потребление2 (Бобков, Гулюгина, 2023). Соответственно, межрегиональное неравенство покупательной способности населения по денежным доходам измеряет разрывы среднего уровня жизни у населения российских регионов3.

Опираясь на тематические труды (Ибрагимова, Франц, 2020; Дорофеев, 2021; Шаталова, Касаткина, 2022 и др.), можно сделать вывод, что для оценки социального неравенства по доходам и богатству в России (ресурсное неравенство) и за рубежом, как правило, применяют несколько показателей (коэффициентов или индексов): коэффициент Джини, коэффициент фондов, децильный коэффициент, семейство обобщенных мер энтропии, T- и L-индексы Тейла, а также семейство индексов неравенства

Аткинсона. При этом в работе (Ибрагимова, Франц, 2020, с. 77) справедливо отмечается, что наиболее распространенным показателем неравенства по доходам и богатству является коэффициент Джини. Помимо него, исследователи в вышеуказанной работе с целью изучения вклада неравенства возможностей в неравенство доходов и заработной платы в РФ применяли L-, T-индексы Тейла и индексы Аткинсона.

Потребность производить более точные измерения привела к использованию в межрегиональных сопоставлениях индексного метода, в рамках которого интегральный показатель (индекс) включает несколько частных индексов. В работе (Симионеску и др., 2020) с целью оценки кадровой региональной дифференциации применялся интегральный индекс, учитывающий шесть базовых компонент (частных индексов) трудового потенциала субъектов РФ: 1) продолжительность трудовой жизни; 2) уровень трудовой активности населения; 3) уровень профессиональной подготовки занятого населения; 4) фондовооруженность труда работников; 5) среднедушевой валовой региональный продукт и 6) среднемесячная заработная плата работников. Исходя из этого перечня, можно сделать вывод, что исследователи одновременно изучают несколько видов социальных неравенств (в частности, по занятости, доходам и уровню образования).

В настоящее время результаты, полученные индексным методом, могут быть существенно дополнены путем применения искусственных нейронных сетей или методов машинного обучения. Так, в частности, метод интеллектуального анализа данных «случайный лес» (см., например, Breiman, 2001) позволяет выявлять скрытые взаимозависимости между различными индикаторами (Зарова, Дубравская, 2020), исследуя влияние экономических показателей на уровень неформальной занятости в российских регионах.

Необходимо отметить, что в последнее время начали появляться работы, не ограничивающиеся ретроспективной оценкой изучаемого феномена с помощью индексного метода. В них проводится многомерный кластерный анализ, дополняющий результаты рейтингования субъектов РФ, причем такой анализ осуществляется и с применением различных методов искусственного интеллекта (ИИ).

Например, исследование (Леонидова и др., 2022) посвящено измерению доходного неравенства населения российских регионов с помощью искусственного интеллекта. Проводится многомерный кластерный анализ по пяти частным показателям (индикаторам): 1) среднедушевые денежные доходы; 2) среднемесячная номинальная начисленная заработная плата; 3) численность населения с доходами ниже величины прожиточного минимума; 4) коэффициент Джини и 5) коэффициент фондов. Иерархическое объединение (см., например, Shetty, Singh, 2021) субъектов РФ по изучаемому явлению в кластер производится методом Варда с применением библиотеки Orange машинного обучения языка программирования Python. Однако до сих пор практически отсутствуют статьи российских ученых, реализующие на основе ИИ прогностическую функцию. При этом за рубежом, наоборот, известно достаточно много работ с применением искусственных нейронных сетей для перспективной оценки социально-экономических характеристик различных систем (Qiu et al., 2019; Jin et al., 2022; Zhang et al., 2022 и др.).

Данные и методы исследования

В данном исследовании совмещены индексный метод и применение искусственного интеллекта для определения индекса уровня жизни, который назван авторами индексом социального благополучия населения . Проведено оценивание межрегионального неравенства уровня жизни по данному индексу. Результаты исследования дополняют способы оценивания уровня жизни населения и его межрегиональные сопоставления. Ретроспективная оценка углубляется путем кластеризации регионов России по индексу социального благополучия населения. Также реализована прогностическая функция динамики вышеуказанного индекса.

Гипотеза исследования состоит в том, что индекс социального благополучия населения позволяет более точно измерить уровень жизни населения. Из этого вытекает достаточно корректное определение межрегионального неравенства уровня жизни населения. Задачи (кластеризация и прогнозирование) в рамках работы решались с применением искусственного интеллекта (искусственных нейронных сетей). Все это составляет элементы новизны исследования.

В рамках работы предпринята попытка соединить в индексе социального благополучия региона оценивание уровня жизни через свертку частных индексов, в центре которых индекс покупательной способности заработной платы, дополненный рядом других, с применением искусственного интеллекта, способного обеспечить высокую точность аппроксимации исходных данных региональной статистики и последующего прогнозирования. Полученный таким комбинированным способом индекс социального благополучия положен авторами в основу выявления и прогнозирования межрегионального неравенства уровня жизни населения. Полагаем, что определение индекса социального благополучия может быть одним из адекватных инструментов для мониторинга текущей ситуации, связанной с уровнем жизни населения, прогноза возможных изменений и сокращения его межрегиональных разрывов. В данном исследовании с учетом вышеизложенных подходов к определению индикаторов изучения уровня жизни предпринята попытка с помощью последовательных итераций предложить адекватную (высокоточную) эконометрическую модель его оценивания и применения для межрегиональных сопоставлений. В исходной позиции с учетом тематических исследований (Ибрагимова, Франц, 2020; Жи-тин, Прокофьев, 2022) считаем возможным предложить следующую систему факторных показателей:

1) среднемесячная номинальная начисленная заработная плата работников организаций (X₁), руб.;
2) численность занятых, приходящихся на одного пенсионера (X₂), чел.;
3) уровень занятости населения в возрасте 15–72 лет (X₃), %;
4) уровень участия в рабочей силе населения в возрасте 15–72 лет (X₄), %;
5) доля населения с денежными доходами ниже величины прожиточного минимума / границы бедности, 2021–2022 гг. (X₅), %;
6) удельный вес городского населения (X₆), %;
7) удельный вес занятого населения с высшим образованием (X₇), %;
8) удельный вес индивидуальных предпринимателей (X₈), %.

Таблица 1. Матрица парных коэффициентов корреляции К. Пирсона

Показатель	Y	X 1	X 2	X 3	X 4	X 5	X 6	X 7	X 8
Y	1
X 1	0,920	1
X 2	0,679	0,608	1
X 3	0,649	0,517	0,637	1
X 4	0,573	0,480	0,684	0,842	1
X 5	-0,560	-0,358	-0,309	-0,642	-0,336	1
X 6	0,478	0,437	0,397	0,637	0,457	-0,554	1
X 7	0,306	0,251	0,432	0,097	0,181	-0,085	0,084	1
X 8	0,181	0,158	0,051	0,253	0,060	-0,198	0,108	0,018	1
Источник: составлено авторами.

Оценим силу влияния каждого из факторов на результативный показатель (Y, среднедушевые денежные доходы населения) на основе расчета и анализа парных коэффициентов корреляции К. Пирсона по данным региональной статистики за 2015–2022 гг.⁴ (табл. 1) .

Первый фактор оказывает сильное влияние на результативный показатель. Между группой факторов (со второго по шестой) и результативным показателем существует прямая (за исключением пятого фактора) связь средней силы. Наконец, седьмой и восьмой факторы слабо влияют на результативный показатель, следовательно, включать их в модель нецелесообразно. Необходимо отметить, что третий и четвертый факторы сильно связаны между собой, однако значение их парного коэффициента корреляции К. Пирсона не превышает 0,85. Отсюда мультиколлинеарность в исходных данных отсутствует, следовательно, для формирования ряда эконометрических моделей может применяться система из первых шести факторов. По результатам корреляционно-регрессионного анализа были исключены третий и шестой факторы. Параметр уравнения регрессии для третьего фактора оказался незначимым. Помимо этого, у вышеуказанных факторов был некорректный (отрицательный) знак в уравнении регрессии, противоречащий социальноэкономическому смыслу. Результаты проверки ряда эконометрических моделей на адекватность (точность аппроксимации исходных данных) представлены в таблице 2.

Согласно значению коэффициентов детерминации (превышающих 0,9), каждая из трех эконометрических моделей позволяет с высокой степенью точности прогнозировать значение результативного показателя. Однако, исходя из средней ошибки аппроксимации (Е), принимающей значения более 8%, все модели обеспечивают лишь приемлемую точность прогнозирования. Поэтому далее в рамках исследования с целью построения высокоточной модели, оценивающей социальное благополучие населения субъектов РФ, применяется индексный метод в сочетании с искусственным интеллектом. Полученный индекс является индексом социального благополучия населения. С учетом результатов ранее проведенного корреляционнорегрессионного анализа частными являются

Таблица 2. Оценка адекватности ряда эконометрических моделей

Модель	Вид уравнения регрессии	R²	Нормированный R²	E, %
Первая	Y=-1916,4+0,504X₁+5428,3X₂+188,8X₄-591X₅	0,924	0,923	8,8
Вторая	Y=8469,2+0,506X₁+7068,2X₂-609,2X₅	0,922	0,922	8,9
Третья	Y=17523,4+0,567X₁-648,8X₅	0,907	0,907	9,6
Источник: составлено авторами.

4 Регионы России. Социально-экономические показатели. 2023: стат. сб. М.: Росстат.

индексы шести первых факторных показателей. Расчет индекса социального благополучия населения производится при следующих основных условиях.

1. Все частные индексы считаются равнозначными. «Свертка» осуществляется по формуле простой среднеарифметической.
2. Учитывается необходимость подчинения исходной информации закону нормального распределения, т. е. асимметрия не должна превышать 0,5. С целью снижения значения показателя (при необходимости) применяется процедура трансформации исходной информации (извлекается корень второй или третьей степени из нормализованных значений частных показателей)⁵.
3. Нормализация значений частных показателей осуществляется максиминным способом. При этом размах вариации определяется в погодовом разрезе.
4. Рост значений частных показателей в динамике является позитивной тенденцией, за исключением пятого фактора.
5. Первый фактор в расчетах фигурирует в сопоставимых ценах для всех регионов России. За базу сравнения принимается стоимость фиксированного набора потребительских товаров и услуг в г. Москве, для других субъектов РФ вводятся поправочные коэффициен-
ты. Вследствие этого первый частный индекс представляет собой индекс покупательной способности населения региона по среднемесячной номинальной начисленной заработной плате работников организаций. Он оказывает наиболее сильное влияние на интегральный индекс социального благополучия населения, который в результате произведенных преобразований представляет собой авторский интегральный индекс уровня жизни населения региона.

Результаты исследования

Результаты расчета индекса социального благополучия населения и последующего ранжирования (формирование рейтинга) регионов России представлены в таблице 3 .

Коэффициент межрегиональной дифференциации индекса социального благополучия населения (рассчитывается как отношение наибольшего значения индекса к наименьшему) составил 4,74 раза в 2015 году, 3,67 раза в 2016 году, 3,85 раза в 2017 году, 4,32 раза в 2018 году, 4,41 раза в 2019 году, 3,97 раза в 2020 году, 3,92 раза в 2021 году и 3,65 раза в 2022 году. В период 2019–2022 гг. дифференциация субъектов РФ по индексу социального благополучия населения снижалась. В 2022 году по сравнению с 2015 годом значение коэффициента сократилось в 1,3 раза.

Таблица 3. Индекс / рейтинг социального благополучия населения субъектов РФ

Субъект РФ	Значение индекса ( y ) / Ранг согласно значению y
Субъект РФ	2015 г.	2016 г.	2017 г.	2018 г.	2019 г.	2020 г.	2021 г.	2022 г.
Белгородская область	0,613/ 29	0,627/ 21	0,649/ 19	0,602/ 21	0,606/ 19	0,641/ 15	0,638/ 21	0,642/ 19
Брянская область	0,512/ 61	0,511/ 60	0,516/ 58	0,451/ 60	0,453/ 62	0,466/ 62	0,482/ 63	0,469/ 67
Владимирская область	0,598/ 32	0,573/ 34	0,597/ 32	0,530/ 39	0,556/ 33	0,569/ 32	0,581/ 33	0,620/ 25
Воронежская область	0,557/ 47	0,555/ 46	0,583/ 37	0,532/ 37	0,544/ 35	0,568/ 33	0,589/ 30	0,597/ 30
Ивановская область	0,560/ 45	0,548/ 51	0,585/ 35	0,484/ 52	0,497/ 48	0,494/ 51	0,557/ 40	0,559/ 41
Калужская область	0,656/ 18	0,662/ 14	0,674/ 14	0,644/ 13	0,628/ 14	0,656/ 14	0,677/ 13	0,666/ 16
Костромская область	0,527/ 58	0,534/ 56	0,550/ 54	0,472/ 55	0,487/ 52	0,502/ 48	0,508/ 54	0,500/ 58

5 Рейтинг инновационного развития субъектов Российской Федерации (2023). Выпуск 8 / В.Л. Абашкин, Г.И. Абдрахманова, С.В. Бредихин и др.; под ред. Л.М. Гохберга; Национальный исследовательский университет «Высшая школа экономики». М.: НИУ ВШЭ. С. 52.

Продолжение таблицы 3

Субъект РФ	Значение индекса ( y ) / Ранг согласно значению y
Субъект РФ	2015 г.	2016 г.	2017 г.	2018 г.	2019 г.	2020 г.	2021 г.	2022 г.
Курская область	0,566/ 43	0,560/ 43	0,579/ 40	0,521/ 41	0,534/ 39	0,543/ 41	0,578/ 34	0,568/ 37
Липецкая область	0,589/ 34	0,594/ 28	0,619/ 26	0,573/ 27	0,580/ 26	0,606/ 23	0,609/ 27	0,617/ 26
Московская область	0,734/ 8	0,733/ 7	0,763/ 7	0,747/ 7	0,737/ 7	0,740/ 7	0,738/ 9	0,728/ 8
Орловская область	0,484/ 67	0,481/ 67	0,486/ 67	0,405/ 69	0,382/ 73	0,414/ 70	0,433/ 70	0,417/ 71
Рязанская область	0,475/ 68	0,483/ 65	0,509/ 61	0,422/ 65	0,472/ 56	0,462/ 63	0,471/ 65	0,496/ 59
Смоленская область	0,573/ 39	0,550/ 49	0,577/ 41	0,504/ 46	0,463/ 59	0,491/ 54	0,510/ 53	0,540/ 46
Тамбовская область	0,499/ 63	0,491/ 63	0,513/ 60	0,434/ 64	0,442/ 65	0,480/ 56	0,491/ 62	0,506/ 57
Тверская область	0,607/ 30	0,590/ 29	0,618/ 28	0,573/ 26	0,573/ 28	0,586/ 28	0,585/ 32	0,587/ 34
Тульская область	0,613/ 28	0,612/ 26	0,625/ 24	0,576/ 25	0,585/ 25	0,616/ 21	0,626/ 24	0,629/ 21
Ярославская область	0,670/ 13	0,648/ 17	0,655/ 17	0,604/ 20	0,590/ 23	0,614/ 22	0,641/ 20	0,628/ 22
город Москва	0,905/ 1	0,920/ 1	0,925/ 1	0,942/ 1	0,922/ 1	0,934/ 1	0,957/ 1	0,928/ 1
Республика Карелия	0,505/ 62	0,514/ 59	0,508/ 64	0,448/ 61	0,473/ 55	0,477/ 59	0,475/ 64	0,467/ 68
Республика Коми	0,643/ 20	0,615/ 25	0,603/ 31	0,564/ 28	0,559/ 32	0,553/ 38	0,546/ 44	0,530/ 49
Архангельская область	0,562/ 44	0,547/ 53	0,573/ 43	0,511/ 44	0,513/ 42	0,515/ 47	0,540/ 46	0,527/ 51
Вологодская область	0,570/ 41	0,577/ 33	0,560/ 49	0,493/ 48	0,510/ 44	0,544/ 40	0,523/ 50	0,530/ 50
Калининградская область	0,662/ 16	0,638/ 19	0,639/ 21	0,586/ 24	0,600/ 21	0,597/ 26	0,610/ 25	0,624/ 24
Ленинградская область	0,651/ 19	0,641/ 18	0,673/ 15	0,615/ 17	0,607/ 18	0,625/ 19	0,642/ 19	0,697/ 12
Мурманская область	0,739/ 7	0,731/ 8	0,745/ 8	0,707/ 8	0,707/ 8	0,707/ 9	0,748/ 7	0,728/ 9
Новгородская область	0,604/ 31	0,586/ 30	0,592/ 33	0,523/ 40	0,511/ 43	0,493/ 53	0,545/ 45	0,531/ 48
Псковская область	0,491/ 66	0,489/ 64	0,471/ 69	0,416/ 67	0,451/ 63	0,439/ 66	0,497/ 59	0,478/ 63
город Санкт-Петербург	0,850/ 3	0,856/ 3	0,882/ 2	0,880/ 2	0,858/ 3	0,879/ 2	0,906/8 3	0,893/ 3
Республика Адыгея	0,347/ 80	0,302/ 80	0,309/ 80	0,279/ 77	0,333/ 76	0,363/ 75	0,305/ 77	0,323/ 77
Республика Калмыкия	0,387/ 77	0,406/ 73	0,410/ 76	0,328/ 76	0,321/ 77	0,375/ 74	0,349/ 74	0,377/ 73
Республика Крым	0,426/ 74	0,388/ 75	0,439/ 73	0,363/ 74	0,413/ 68	0,438/ 67	0,442/ 69	0,432/ 70
Краснодарский край	0,539/ 54	0,540/ 54	0,563/ 46	0,514/ 43	0,515/ 41	0,538/ 42	0,548/ 43	0,549/ 43
Астраханская область	0,614/ 27	0,585/ 31	0,630/ 23	0,541/ 35	0,537/ 38	0,554/ 37	0,563/ 39	0,581/ 35

Продолжение таблицы 3

Субъект РФ	Значение индекса ( y ) / Ранг согласно значению y
Субъект РФ	2015 г.	2016 г.	2017 г.	2018 г.	2019 г.	2020 г.	2021 г.	2022 г.
Волгоградская область	0,577/ 37	0,564/ 40	0,575/ 42	0,540/ 36	0,525/ 40	0,556/ 36	0,575/ 35	0,597/ 29
Ростовская область	0,529/ 57	0,548/ 52	0,553/ 53	0,492/ 49	0,498/ 47	0,532/ 43	0,550/ 42	0,566/ 38
город Севастополь	0,617/ 25	0,566/ 37	0,606/ 30	0,608/ 19	0,614/ 16	0,605/ 24	0,652/ 15	0,667/ 14
Республика Дагестан	0,413/ 75	0,405/ 74	0,411/ 75	0,337/ 75	0,354/ 75	0,321/ 77	0,310/ 76	0,352/ 74
Республика Ингушетия	0,369/ 78	0,372/ 76	0,444/ 72	0,386/ 72	0,396/ 70	0,391/ 71	0,346/ 75	0,344/ 75
Кабардино-Балкарская Республика	0,471/ 69	0,440/ 72	0,450/ 71	0,421/ 66	0,414/ 67	0,440/ 65	0,462/ 66	0,471/ 66
Карачаево-Черкесская Республика	0,311/ 81	0,281/ 81	0,263/ 81	0,219/ 81	0,218/ 81	0,235/ 82	0,255/ 81	0,282/ 80
Республика Северная Осетия – Алания	0,465/ 71	0,440/ 71	0,487/ 66	0,473/ 54	0,379/ 74	0,323/ 76	0,379/ 73	0,409/ 72
Чеченская Республика	0,409/ 76	0,366/ 78	0,350/ 78	0,265/ 78	0,281/ 78	0,263/ 81	0,276/ 80	0,269/ 81
Ставропольский край	0,513/ 60	0,509/ 61	0,509/ 62	0,456/ 59	0,482/ 53	0,498/ 50	0,500/ 57	0,509/ 56
Республика Башкортостан	0,552/ 51	0,548/ 50	0,557/ 50	0,480/ 53	0,474/ 54	0,493/ 52	0,507/ 55	0,521/ 53
Республика Марий Эл	0,518/ 59	0,495/ 62	0,496/ 65	0,394/ 70	0,428/ 66	0,422/ 69	0,446/ 68	0,448/ 69
Республика Мордовия	0,557/ 46	0,558/ 44	0,556/ 52	0,461/ 58	0,510/ 45	0,472/ 61	0,521/ 51	0,562/ 39
Республика Татарстан	0,715/ 9	0,705/ 9	0,716/ 9	0,671/ 10	0,667/ 10	0,690/ 11	0,710/ 10	0,715/ 10
Удмуртская Республика	0,639/ 21	0,619/ 23	0,619/ 27	0,557/ 31	0,541/ 36	0,570/ 31	0,571/ 36	0,560/ 40
Чувашская Республика	0,570/ 42	0,530/ 57	0,520/ 57	0,448/ 62	0,456/ 61	0,474/ 60	0,494/ 61	0,488/ 61
Пермский край	0,578/ 36	0,571/ 35	0,562/ 47	0,493/ 47	0,498/ 46	0,531/ 44	0,552/ 41	0,541/ 45
Кировская область	0,554/ 49	0,553/ 48	0,567/ 44	0,509/ 45	0,488/ 51	0,519/ 46	0,527/ 49	0,523/ 52
Нижегородская область	0,663/ 15	0,667/ 12	0,685/ 12	0,636/ 14	0,636/ 13	0,662/ 13	0,673/ 14	0,679/ 13
Оренбургская область	0,556/ 48	0,554/ 47	0,567/ 45	0,517/ 42	0,458/ 60	0,483/ 55	0,496/ 60	0,472/ 65
Пензенская область	0,553/ 50	0,561/ 41	0,529/ 56	0,492/ 50	0,469/ 57	0,478/ 57	0,530/ 48	0,481/ 62
Самарская область	0,675/ 12	0,666/ 13	0,665/ 16	0,626/ 15	0,611/ 17	0,637/ 16	0,650/ 16	0,656/ 17
Саратовская область	0,551/ 52	0,536/ 55	0,515/ 59	0,446/ 63	0,495/ 50	0,499/ 49	0,514/ 52	0,547/ 44
Ульяновская область	0,550/ 53	0,557/ 45	0,557/ 51	0,466/ 57	0,466/ 58	0,477/ 58	0,504/ 56	0,532/ 47
Курганская область	0,429/ 73	0,368/ 77	0,367/ 77	0,258/ 79	0,264/ 79	0,309/ 78	0,277/ 79	0,284/ 79
Свердловская область	0,681/ 11	0,651/ 16	0,651/ 18	0,591/ 23	0,604/ 20	0,617/ 20	0,642/ 18	0,625/ 23

Окончание таблицы 3

Субъект РФ	Значение индекса ( y ) / Ранг согласно значению y
Субъект РФ	2015 г.	2016 г.	2017 г.	2018 г.	2019 г.	2020 г.	2021 г.	2022 г.
Тюменская область	0,763/ 5	0,761/ 5	0,777/ 5	0,761/ 6	0,747/ 6	0,748/ 6	0,760/ 6	0,749/ 6
Челябинская область	0,665/ 14	0,656/ 15	0,682/ 13	0,661/ 12	0,661/ 11	0,673/ 12	0,684/ 12	0,666/ 15
Республика Алтай	0,351/ 79	0,327/ 79	0,324/ 79	0,241/ 80	0,260/ 80	0,301/ 79	0,282/ 78	0,254/ 82
Республика Тыва	0,191/ 82	0,251/ 82	0,240/ 82	0,218/ 82	0,209/ 82	0,290/ 80	0,244/ 82	0,291/ 78
Республика Хакасия	0,530/ 55	0,515/ 58	0,531/ 55	0,467/ 56	0,447/ 64	0,437/ 68	0,498/ 58	0,510/ 55
Алтайский край	0,495/ 65	0,468/ 69	0,468/ 70	0,378/ 73	0,395/ 71	0,387/ 72	0,407/ 71	0,474/ 64
Красноярский край	0,498/ 64	0,483/ 66	0,508/ 63	0,594/ 22	0,595/ 22	0,600/ 25	0,633/ 23	0,612/ 28
Иркутская область	0,595/ 33	0,583/ 32	0,581/ 39	0,531/ 38	0,540/ 37	0,546/ 39	0,565/ 38	0,587/ 33
Кемеровская область	0,616/ 26	0,609/ 27	0,610/ 29	0,543/ 34	0,555/ 34	0,565/ 34	0,571/ 37	0,572/ 36
Новосибирская область	0,624/ 23	0,627/ 20	0,638/ 22	0,564/ 29	0,577/ 27	0,579/ 30	0,610/ 26	0,596/ 31
Омская область	0,629/ 22	0,616/ 24	0,620/ 25	0,563/ 30	0,563/ 30	0,594/ 27	0,596/ 29	0,592/ 32
Томская область	0,530/ 56	0,566/ 38	0,561/ 48	0,552/ 32	0,560/ 31	0,562/ 35	0,586/ 31	0,557/ 42
Республика Бурятия	0,471/ 70	0,442/ 70	0,428/ 74	0,405/ 68	0,384/ 72	0,384/ 73	0,381/ 72	0,331/ 76
Республика Саха (Якутия)	0,588/ 35	0,561/ 42	0,585/ 36	0,615/ 16	0,622/ 15	0,629/ 17	0,637/ 22	0,635/ 20
Забайкальский край	0,576/ 38	0,568/ 36	0,581/ 38	0,487/ 51	0,496/ 49	0,521/ 45	0,533/ 47	0,520/ 54
Камчатский край	0,702/ 10	0,678/ 10	0,686/ 11	0,675/ 9	0,694/ 9	0,723/ 8	0,739/ 8	0,735/ 7
Приморский край	0,623/ 24	0,626/ 22	0,645/ 20	0,610/ 18	0,589/ 24	0,628/ 18	0,648/ 17	0,648/ 18
Хабаровский край	0,656/ 17	0,676/ 11	0,701/ 10	0,669/ 11	0,638/ 12	0,697/ 10	0,699/ 11	0,705/ 11
Амурская область	0,573/ 40	0,564/ 39	0,592/ 34	0,550/ 33	0,564/ 29	0,585/ 29	0,599/ 28	0,615/ 27
Магаданская область	0,842/ 4	0,824/ 4	0,868/ 4	0,863/ 4	0,836/ 4	0,876/ 4	0,912/ 2	0,897/ 2
Сахалинская область	0,746/ 6	0,747/ 6	0,769/ 6	0,783/ 5	0,765/ 5	0,787/ 5	0,796/ 5	0,809/ 5
Еврейская автономная область	0,464/ 72	0,469/ 68	0,475/ 68	0,394/ 71	0,412/ 69	0,456/ 64	0,451/ 67	0,488/ 60
Чукотский автономный округ	0,861/ 2	0,863/ 2	0,876/ 3	0,875/ 3	0,866/ 2	0,877/ 3	0,882/ 4	0,877/ 4
Miny	0,191	0,251	0,240	0,218	0,209	0,235	0,244	0,254
Maxy	0,905	0,920	0,925	0,942	0,922	0,934	0,957	0,928

Примечание: Архангельская область указана в составе с Ненецким автономным округом, а Тюменская область – с Ханты-Мансийским автономным округом – Югрой и Ямало-Ненецким автономным округом.

Источник: составлено авторами.

Лидерами рейтинга (первые пять мест) в анализируемом периоде являлись г. Москва и Санкт-Петербург, Магаданская область, Чукотский автономный округ и Сахалинская область. При этом необходимо отметить, что на протяжении всего анализируемого периода даже у безусловного лидера рейтинга – г. Москвы – значение индекса было менее 1, следовательно, столица не является абсолютным лидером, т. е. лидером по всем шести частным индексам одновременно. В состав аутсайдеров рейтинга (последние пять мест) также на регулярной основе входили Чеченская Республика, Карачаево-Черкесская Республика, Республика Алтай, Курганская область и Республика Тыва.

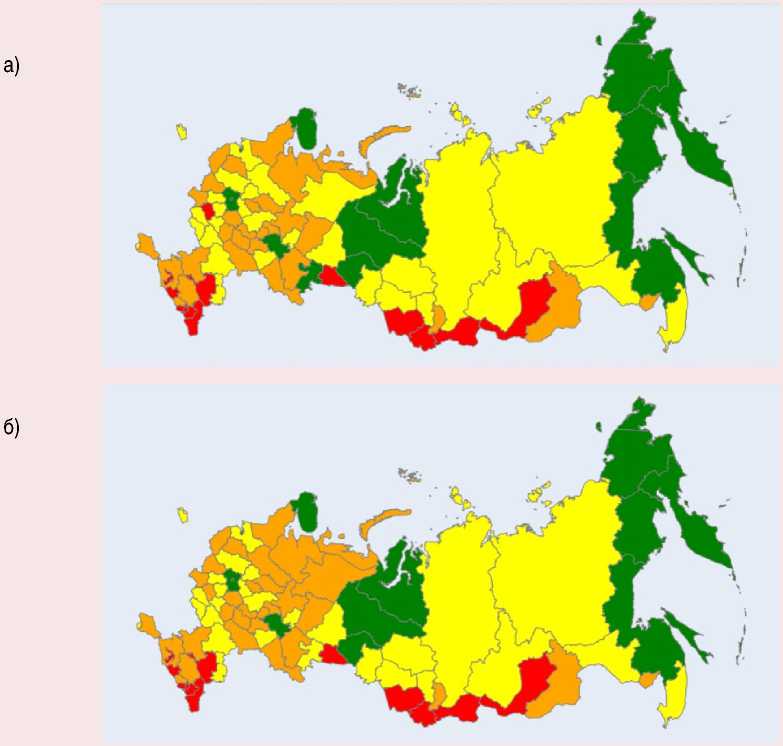
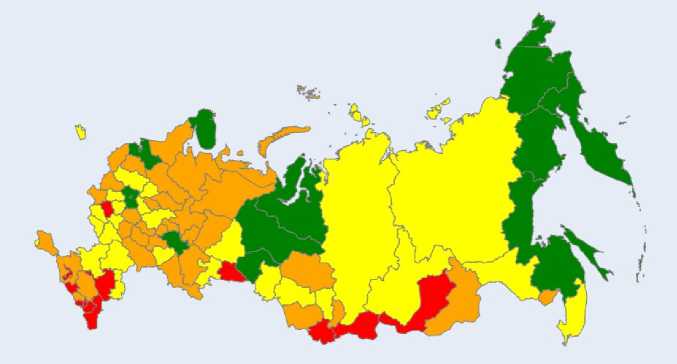
Далее на примере 2020–2022 гг. проводится кластеризация субъектов РФ по индексу социального благополучия населения с помощью искусственного интеллекта. Кластерный анализ осуществляется методом самоорганизующихся карт Т. Кохонена в демо-версии программного продукта Deductor Studio Lite 5.1. Обучение каждой такой карты производится при следующих основных условиях: 1) способ начальной инициализации – обучающее множество; 2) Гауссова функция соседства. Исходя из расчета и анализа наибольшего и наименьшего значений индекса принято решение о целесо- образности выделения четырех кластеров регионов России, характеризующихся высоким, выше среднего, средним и ниже среднего уровнем социального благополучия населения. Результаты ежегодного распределения субъектов РФ согласно y представлены на рисунке 1.

Далее проанализируем изменения в кластерной структуре российских регионов (табл. 4) . Большая часть (порядка 70–72%) субъектов страны в 2020–2022 гг. характеризовалась либо выше среднего, либо средним уровнем индекса социального благополучия населения. При этом на разных «полюсах» (примерно по 13– 15%) ежегодно располагались регионы с высоким и ниже среднего уровнем индекса социального благополучия населения.

Необходимо отметить устойчивость сформировавшейся кластерной структуры субъектов РФ на протяжении последних трех лет анализируемого периода. Практически неизменным оставалось количество регионов как в первом, так и в четвертом кластерах. Незначительные (по количеству) переходы регионов России наблюдались лишь между вторым и третьим кластерами.

Корректность процедуры (кластерного анализа с применением искусственного интеллекта) подтверждается рядом показателей (табл. 5) .

Таблица 4. Кластерная структура субъектов РФ по индексу социального благополучия населения

Кластер	2020 год		2021 год		2022 год
Кластер	число регионов	%	число регионов	%	число регионов	%
Первый	12	14,6	11	13,4	12	14,6
Второй	29	35,4	28	34,1	26	31,7
Третий	28	34,1	31	37,8	32	39,0
Четвертый	13	15,9	12	14,6	12	14,6
Источник: составлено авторами.

Таблица 5. Оценка адекватности процедуры кластеризации субъектов РФ в Deductor Studio Lite 5.1

Показатель	2020 год	2021 год	2022 год
Максимальная ошибка	2,58Е-0,3	7,91Е-0,3	2,88Е-0,3
Средняя ошибка	2,83Е-0,4	6,83Е-0,4	3,63Е-0,4
Распознано (%)	100	100	100
Источник: составлено авторами.

Рис. 1. Распределение субъектов РФ по индексу социального благополучия населения в 2020 (а), 2021 (б), 2022 (в) году

в)

Примечание:

первый кластер

второй кластер

третий кластер

четвертый кластер

Источник: составлено авторами.

Все наблюдения ежегодно были полностью распознаны. На устойчивость полученных результатов также указывает одинаковый порядок в 2020–2022 гг. как средней, так и максимальной ошибки. Далее реализуется прогностическая функция также с помощью искусственного интеллекта в демоверсии программного продукта Deductor Studio Lite 5.1. Ввиду ограничения по количеству наблюдений (не более 150) нейромоделирование осуществляется на примере 50 субъектов РФ, входящих в Центральный, Северо-Западный, Южный, Северо-Кавказский, Уральский и Дальневосточный федеральные округа, за 2020–2022 гг.

«Выходная» переменная – индекс социального благополучия населения. К «входным» переменным относятся первый, второй, четвертый и пятый факторы. По причине относительно малого массива данных обучение нейромо- делей осуществляется на всем множестве наблюдений. Конфигурация сформированного байесовского ансамбля нейромоделей представлена в таблице 6.

В байесовский ансамбль были включены пять нейромоделей либо с одним, либо с двумя скрытыми слоями. При этом варьировалось число нейронов в скрытых слоях с шагом – 4.

Оценим адекватность сформированного байесовского ансамбля нейромоделей с помощью как автоматически определяемых, так и самостоятельно рассчитанных показателей ( табл. 7, 8 ). Во втором случае дополнительно определяются средняя (Е) и максимальная ошибка (maxe) аппроксимации исходных данных, также рассчитывается частотный критерий качества нейромоделирования (количество (N) и процент (P) корректно распознанных наблюдений при 5 и 8% индивидуальной ошибке аппроксимации).

Таблица 6. Конфигурация байесовского ансамбля нейромоделей

Нейромодель	Количество скрытых слоев	Число нейронов		Активационная функция
Нейромодель	Количество скрытых слоев	в первом скрытом слое	во втором скрытом слое	Активационная функция
Первая	1	4	-	Гипертангенс
Вторая	1	8	-
Третья	1	12	-
Четвертая	2	8	8
Пятая	2	8	12
Источник: составлено авторами.

Таблица 7. Система автоматически рассчитанных показателей адекватности байесовского ансамбля нейромоделей

Нейромодель	Максимальная ошибка	Средняя ошибка	Распознано (%)
Первая	9,13Е-0,3	1,23Е-0,3	100
Вторая	9,17Е-0,3	9,35Е-0,4	100
Третья	1,08Е-0,2	1,23Е-0,3	100
Четвертая	5,32Е-0,3	4,87Е-0,4	100
Пятая	5,65Е-0,3	5,17Е-0,4	100
Источник: составлено авторами.

Таблица 8. Дополнительные показатели адекватности байесовского ансамбля нейромоделей

Нейромодель	Е, %	N		P		maxe, %
Нейромодель	Е, %	e = 5%	e = 8%	e = 5%	e = 8%	maxe, %
Первая	3,7	109	140	72,7	93,3	13,9
Вторая	2,8	127	143	84,7	95,3	14,4
Третья	3,3	117	142	78	94,7	13,6
Четвертая	3,9	104	135	69,3	90	11,3
Пятая	3,6	110	138	73,3	92	10,8
Источник: составлено авторами.

Согласно как средней, так и максимальной ошибке наиболее адекватной из пяти нейромоделей является четвертая искусственная нейронная сеть. Близкие с ней значения показателей демонстрирует пятая нейромодель.

Если исходя из средней ошибки аппроксимации и частотного критерия качества наиболее адекватной является вторая нейромодель, то согласно максимальной ошибке аппроксимации – пятая искусственная нейронная сеть. Учитывая значения всех показателей адекватности, можно сделать вывод, что искусственный интеллект позволяет с высокой степенью точности аппроксимировать исходные данные, необходимые для формирования прогноза по индексу социального благополучия населения субъектов РФ.

Реализуем прогностическую функцию с помощью сформированного байесовского ансамбля нейромоделей на примере регионов-лидеров рейтинга для 2024–2025 гг. (табл. 9, рис. 2) . При этом значения факторных показателей назначены экспертами исходя из тенденций их изменения в динамике за 2015–2022 гг. Согласно данным сформированного прогноза, в 2024–2025 гг. ожидается сохранение лидерства г. Москвы по индексу социального благополучия населения.

При этом прогнозируется практически фиксация значения результативного показателя у региона-лидера. На 2–3-м местах рейтинга предположительно расположатся, соответственно, Магаданская область и г. Санкт-Петербург. При этом для каждого из двух вышеука-

Таблица 9. Прогнозирование индекса социального благополучия населения (у) с помощью искусственного интеллекта

Субъект РФ	2024 год (оценка)					2025 год (оценка)
Субъект РФ	x₁	x₂	x₄	x₅	^y	x₁	x₂	x₄	x₅	^y
г. Москва	0,995	1,000	0,910	0,997	0,945	0,997	1,000	0,915	0,998	0,946
г. Санкт-Петербург	0,905	0,810	0,905	1,000	0,905	0,910	0,820	0,910	1,000	0,908
Магаданская область	1,000	0,800	0,980	0,900	0,912	1,000	0,810	0,985	0,910	0,914
Сахалинская область	1,000	0,625	0,890	0,935	0,827	1,000	0,635	0,910	0,940	0,834
Чукотский автономный округ	0,985	0,870	1,000	0,925	0,885	0,990	0,880	1,000	0,930	0,887
Источник: составлено авторами.

Рис. 2. Индекс социального благополучия населения регионов-лидеров рейтинга

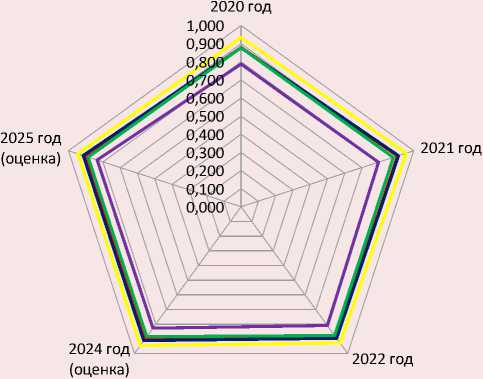
г. Москва

^^^^^m г. Санкт-Петербург

^^^^^и Магаданская область

^^^^^^^^м Сахалинская область

^^^^^^^в Чукотский автономный округ

Источник: составлено авторами.

занных регионов-лидеров рейтинга в 2024– 2025 гг. ожидается рост значения индекса.

Исходя из данных рисунка 2, между 2–4-м регионами-лидерами рейтинга по индексу социального благополучия населения наблюдается высокая плотность итоговых результатов в 2020–2022 гг. и ожидается ее сохранение на протяжении всего периода прогнозирования. При этом необходимо отметить достаточно большой отрыв 5-го места от 4-го в рейтинге индекса.

Таким образом, индексный метод в сочетании с искусственным интеллектом обеспечивает высокую точность оценки по индексу социального благополучия населения субъектов РФ. Полученные в ходе эмпирического исследования результаты могут быть интерпретированы в рамках так называемой ординалистской парадигмы: «увеличивается – уменьшается» (Fleming, 1952).

В настоящее время, как правило, уполномоченными органами власти на мезоуровне составляются прогнозы социально-экономических индикаторов с помощью сценарного подхода, реализуемого экспертами и поэтому отличающегося высокой степенью субъективности. Разработанный инструментарий позволит повысить точность перспективной оценки изучаемого явления.

Обсуждение результатов

В современной России, как справедливо отмечается в работах (Лапин и др., 2020; Черныш, 2021; Пугачев, 2023), наблюдается высокий (или даже избыточный) уровень монетарного неравенства населения по сравнению с рядом стран мира. Идентичный вывод можно сделать самостоятельно, если проанализировать изменение в динамике значения коэффициента Джини по душевым денежным доходам для России при сравнении с другими странами мира.

Необходимо отметить, что в современной России (2000 год – настоящее время) «пик» по коэффициенту Джини по денежным доходам (порядка 0,42–0,422 в 2007–2010 гг. и 2012 году) пройден. В 2022 году значение показателя повторило исторический минимум, зафиксированный в 2000 году (0,395). Помимо этого, в разрезе регионов ситуация существенно отличается от среднероссийской. В ряде из них наблюдается значительно более высокий уро- вень монетарного неравенства населения. Так, в частности, значение коэффициента Джини по денежным доходам в 2022 году в г. Москве составляло 0,412, в Ненецком автономном округе – 0,419, в Тюменской области – 0,426, в Ямало-Ненецком автономном округе – 0,44, в Чукотском автономном округе – 0,41. На другом полюсе находятся регионы с монетарным неравенством существенно ниже среднероссийских значений: Костромская область, Республика Хакасия – 0,320, Республика Калмыкия – 0,313, Республика Ингушетия – 0,311, Еврейская автономная область – 0,3106. Коэффициент межрегиональной дифференциации (отношение наибольшего значения показателя к наименьшему) составляет 1,4 раза.

В 2022 году наиболее высокая покупательная способность населения по душевым денежным доходам зафиксирована в Ямало-Ненецком автономном округе (6,1 ПМ (прожиточных минимума) рег.), г. Москве (4,8 ПМ рег.), г. Санкт-Петербурге (4,6 ПМ рег.), Ненецком автономном округе (4,3 ПМ рег.) и Сахалинской области (4,0 ПМ рег.). На противоположном полюсе располагались Еврейская автономная область (1,9 ПМ рег.), Республика Калмыкия (1,89 ПМ рег.), Карачаево-Черкесская Республика (1,8 ПМ рег.), Республика Ингушетия (1,7 ПМ рег.) и Республика Тыва (1,6 ПМ рег.). Коэффициент межрегиональной дифференциации покупательной способности населения (соотношение наибольшего и наименьшего значения показателя) равен 3,8 (Бобков, Гулюгина, 2023, с. 114, 137–139).

Коэффициент межрегиональной дифференциации индекса социального благополучия населения составил в 2022 году 3,65 раза – 0,96 от значения аналогичного индекса покупательной способности населения, т. е. они имеют близкие значения. Также имеются точки пересечения по распределению субъектов РФ на разных полюсах рейтинга. Например, в группе регионов-лидеров для двух вышеуказанных показателей находятся г. Москва, Санкт-Петербург и Сахалинская область, а в группе регионов-аутсайдеров – Карачаево-Черкесская Республика и Республика Тыва.

Необходимо отметить, что близкие коэффициенты межрегиональной дифференциации по индексу социального благополучия населения и покупательной способности населения значительно выше аналогичного коэффициента, измеряющего межрегиональную дифференциацию распределения ресурсов уровня жизни (в нашем случае – коэффициента Джини по денежным доходам), примерно в 2,6–2,7 раза.

Вместе с тем результаты измерения межрегиональной дифференциации по индексу социального благополучия населения частично не совпадают с результатами его измерения по покупательной способности населения по душевым денежным доходам. По состоянию на 2022 год списки лидеров и аутсайдеров по индексу социального благополучия населения не полностью совпадали: по первому индексу в верхнюю группу, кроме трех совпадающих субъектов, попали ЯмалоНенецкий автономный округ и Ненецкий автономный округ, а в нижнюю группу, кроме двух совпадающих субъектов, попали также Еврейская автономная область, Республика Калмыкия и Республика Ингушетия; по второму индексу, соответственно, Магаданская область, Чукотский автономный округ и Республика Алтай, Чеченская Республика, а также Курганская область.

Это обусловлено учетом в индексе социального благополучия населения большего количества факторов, определяющих его значение, несмотря на то, что определяющим в нем является покупательная способность населения по среднемесячной начисленной заработной плате работников организаций.

Для более детального анализа результатов исследования, включая их прогнозную оценку, т. е. определения, за счет каких факторных показателей произошло / может произойти улучшение или ухудшение индекса социального благополучия населения, необходимо произвести декомпозицию факторов, заложенных в модель определения данного индекса, или воспользоваться параллельным прогнозом покупательной способности населения, являющейся факторным показателем, наиболее сильно влияющим на динамику индекса социального благополучия населения.

Заключение

Учитывая площадь России, разнообразие условий жизни и большое количество регионов, в рамках исследования внимание было сфокусировано на изучении возможностей более точного определения социального благополучия населения для повышения результативности социальной политики на мезоуровне управления и использования индекса социального благополучия населения для оценивания межрегиональной дифференциации уровня жизни. В настоящее время на регулярной основе (ежегодно) проводится оценка результативности деятельности органов исполнительной власти в субъектах РФ. В аспекте уровня жизни она опирается на учет изменений в динамике темпов роста реальных денежных доходов населения и реальной среднемесячной заработной платы. При межрегиональных сопоставлениях уровня жизни населения они, в части официальных оценок, не учитывают региональные различия покупательной способности населения и ряд других факторов, формирующих его уровень жизни, в связи с чем в рамках нашего исследования была предпринята попытка устранить этот недостаток и предложить авторский подход, состоящий в определении индекса социального благополучия населения с помощью искусственного интеллекта, который более точно измеряет динамику уровня жизни и может быть применен для оценки его межрегиональной дифференциации.

Эмпирическим путем было доказано, что индексный метод в сочетании с искусственным интеллектом позволяет с более высокой степенью точности аппроксимировать данные региональной статистики. Так, если для каждой из трех разработанных традиционных эконометрических моделей средняя ошибка аппроксимации составляла порядка 9–10%, то любая из пяти искусственных нейронных сетей, включенных в байесовский ансамбль, позволяла аппроксимировать исходные данные со средней ошибкой в размере 3–4%. Поэтому среднесрочный прогноз социального благополучия населения субъектов РФ на примере регионов-лидеров рейтинга был сформирован с помощью индексного метода и искусственного интеллекта.

Таким образом, результаты, полученные в рамках исследования, могут:

– являться научной базой для принятия эффективных управленческих решений руководством российских регионов по повышению уровня жизни населения;

– применяться федеральными органами власти для оценивания межрегиональной дифференциации уровня жизни по индексу социального благополучия населения;

– ориентировать государственную социальную политику на повышение индекса социального благополучия населения российских регионов и выравнивание его региональных значений.

Авторы не исключают применения одновременно всех рассмотренных выше способов оценивания возможной социальной динамики в регионах Российской Федерации и измерения межрегиональной дифференциации: ресурсного обеспечения уровня жизни (индекса Джини по душевым денежным доходам); покупательной способности населения по душевым денежным доходам и индекса социального благополучия населения. Сопоставление этих показателей позволит выявлять одинаково и разнонаправленные процессы, влияющие на формирование уровня жизни населения, и принимать «взвешенные» управленческие решения. Соответственно, полезно было бы проводить межрегиональные сопоставления по всем трем рассмотренным показателям: индексу Джини по доходам, покупательной способности населения по душевым денежным доходам и индексу социального благополучия населения.

Список литературы Оценка межрегионального неравенства в Российской Федерации по индексу социального благополучия населения

Бобков В.Н., Гулюгина А.А. (2023). Мониторинг доходов и уровня жизни населения России – 2022 год. Выпуск 1 (202). М.: ИЭ РАН.
Бобков В.Н., Одинцова Е.В. (2020). Социальное неравенство в России // Журнал Новой экономической ассоциации. № 3. С. 179–184. DOI: 10.31737/2221-2264-2020-47-3-8
Дорофеев М.Л. (2021). Современная долговая проблема США в контексте регулирования социально-экономического неравенства // Вестник Томского государственного университета. Экономика. № 54. С. 273–286. DOI: 10.17223/19988648/54/16
Житин Д.В., Прокофьев А.Д. (2022). Этнотерриториальные особенности социального неравенства в США // Вестник Санкт-Петербургского университета. Науки о земле. № 2. С. 333–359. DOI: 10.21638/spbu07.2022.207
Зарова Е.В., Дубравская Э.И. (2020). Метод «случайный лес» в исследовании влияния макроэкономических показателей регионального развития на уровень неформальной занятости // Вопросы статистики. № 6. С. 37–55. DOI: 10.34023/2313-6383-2020-27-6-37-55
Ибрагимова З.Ф., Франц М.В. (2020). Неравенство возможностей: теория и практика измерения на микроданных RLMS-HSE // Экономическая политика. № 1. С. 64–89. DOI: 10.18288/1994-5124-2020-1-64-89
Лапин Н.И., Ильин В.А., Морев М.В. (2020). Экстремальные неравенства и социальное государство (часть 1) // Социологические исследования. № 1. С. 4–17. DOI:10.31857/S013216250008378-8
Леонидова Г.В., Басова Е.А., Рассадина М.Н. (2022). Кластерный анализ доходного неравенства населения российских регионов // Проблемы развития территории. № 6. С. 94–114. DOI: 10.15838/ptd.2022.6.122.6
Мерзляков А.А., Богданов В.С. (2022). Об исследовании социолого-управленческих аспектов регулирования социальных неравенств в регионах России // Вестник Института социологии. № 4. С. 130–143. DOI: 10.19181/vis.2022.13.4.853
Пугачев А.А. (2023). Экономическое неравенство граждан за гранью средних показателей: проблемы диагностики в условиях его трансформации // Экономические и социальные перемены: факты, тенденции, прогноз. № 3. С. 141–158. DOI: 10.15838/esc.2023.3.87.7
Симионеску М., Кривокора Е., Фурсов В., Астахова Е. (2020). Проблемы развития трудового потенциала регионов Российской Федерации с учетом их дифференциации // Terra Economicus. № 2. С. 117–138. DOI: 10.18522/2073-6606- 2020-18-2-117-138
Спиридонов А.Ю., Найденова А.А. (2024). Качество жизни населения: подходы к определению понятия, формирование системы сбора данных и методики оценки // Экономика труда. № 8. С. 1159–1180. DOI: 10.18334/et.11.8.121438
Суринов А.Е., Луппов А.Б. (2022). Дифференциация доходов населения и стоимость жизни на субрегиональном уровне. Оценки для России // Экономический журнал ВШЭ. № 4. С. 552–578. DOI: 10.17323/1813-8691-2022-26-4-552-578
Черныш М.Ф. (2021). Институциональные основы неравенства в современном обществе // Мир России. № 3. С. 6–28. DOI: 10.17323/1811-038X-2021-30-3-6-28
Шаталова О.М., Касаткина Е.В. (2022). Социально-экономическое неравенство регионов РФ: вопросы измерения и долгосрочная ретроспективная оценка // Экономические и социальные перемены: факты, тенденции, прогноз. № 4. С. 74–87. DOI: 10.15838/esc.2022.4.82.5
Breiman L. (2001). Random Forests. Machine Learning, 45(1), 5–32. DOI: 10.1023/ A:1010933404324
Fleming M. (1952). A cardinal Concept of Welfare. The American Economic Review, XLI, 287.
Jin N., Yang F., Mo Yu. et al. (2022). Highly accurate energy consumption forecasting model based on parallel LSTM neural networks. Advanced Engineering Informatics, 51, 101442. DOI: 10.1016/j.aei.2021.101442
Qiu J., Wang B., Zhou C. (2019). Forecasting stock prices with long-short term memory neural network based on attention mechanism. PLoS ONE, 2.15(1): e0227222. DOI: https://doi.org/10.1371/journal.pone.0227222
Shetty P., Singh S. (2021). Hierarchical clustering: A survey. International Journal of Applied Research, 7(40), 178–181. DOI: 10.22271/allresearch.2021.v7.i4c.8484
Zhang Q., Abdullah A.R., Chong C.W., Ali M.H.A. (2022). Study on regional GDP forecasting analysis based on Radial Basis Function Neural Network with Genetic Algorithm (RBFNN-GA) for Shandong economy. Computational Intelligence and Neuroscience, 12. DOI: 10.1155/2022/823530

Еще

Статья научная