Оценка области однозначной проекции поверхности отрицательной кривизны
Бесплатный доступ
Рассматривается поверхность с отрицательной гауссовой кривизной, которая однозначно проектируется на круг. Получены достаточные условия, при которых существует оценка для радиуса круга.
Поверхности отрицательной гауссовой кривизны, уравнение монжа-алтера гиперболического типа, оценка области однозначной проекции
Короткий адрес: https://sciup.org/147158753
IDR: 147158753
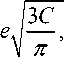
Список литературы Оценка области однозначной проекции поверхности отрицательной кривизны
- Ефимов, Н.В. Исследование полной поверхности отрицательной кривизны/Н.В. Ефимов. -М.: Докл. АН СССР, 1953. -640 с.
- Heinz, E. Über Flachen mit eineindeutiger Projektion auf eine Ebene, deren Krümmungen durch Ungleichungen eingeschränkt sind/E. Heinz//Math. Ann. -1955. -V. 129, № 5. -P. 451-454.
- Ефимов, Н.В. Оценки размеров области регулярности решений некоторых уравнений Монжа-Ампера/Н.В. Ефимов//Математический сборник. -1976. -Т. 100(142), № 3(7). -С. 356-363.
- Азов, Д.Г. Об одном классе гиперболических уравнений Монжа-Ампера/Д.Г. Азов//Успехи математических наук. -1983. -Т. 38, № 1. -С. 153-154.
- Брысьев, А.Б. Оценка области регулярности решений некоторых нелинейных дифференциальных неравенств/А.Б. Брысьев//Украинский геометрический сборник. -1985. -Вып. 28. -С. 19-21.
- Азов, Д.Г. Изометрическое погружение «-мерных метрик в евклидовы и сферические пространства/Д.Г. Азов//Вестник Челябинского государственного университета. -1994. -№ 1(2). -С. 12-17.
- Азов, Д.Г. Погружение методом Д. Блануши некоторых классов полных n-мерных римановых метрик в евклидовы пространства/Д.Г. Азов//Вестник Московского университета. -1985. -№ 5. -С. 72-74.
Статья научная
