Оценка оптимального номера останова итераций при восстановлении импульсной характеристики искажающей системы

Решение задачи идентификации модели искажающей системы часто необходимо при проведении научных исследований и технических испытаний различны х устройств. Как правило, идентификация системы используется для оценки качества работы оборудования с целью обнаружения неполадок и при их наличии коррекции выходных данных.

При невозможности устранения неполадки на аппаратном уровне, например, в устройствах дистанционного зондирования Земли, часто прибегают к созданию цифровых корректирующих систем, позволяющих устранить последствия работы неисправной техники на уровне выходных данных.

Из-за погрешностей наблюдения за реакцией системы, больших объёмов статистических данных, задача идентификации почти всегда плохо обусловлена. Улучшение обусловленности задачи возможно, например, за счёт отбора информативных данных [1-2].

Для систем, допускающих линейное приближение, ставится задача решения стохастической системы линейных алгебраических уравнений (СЛАУ) [3-4]. В предлагаемой работе исследуется способ получения вычислительно устойчивых решений задачи идентификации линейной системы, основанный на применении итерационных методов, обладающих свойством рег уляризации [5-6].

1.    Постановка задачи идентификации

Рассмотрим уравнение линейной искажающей системы типа свёртки

y(n) = Th(k)■ x(n-k), (1) ke D где x (n) и y (n) - входной и выходной сигналы, соответственно, h (n) - импульсная характеристика (ИХ) искажающей системы , заданн ая на конечной области определения D .

Уравнение (1) имеет запись в виде СЛАУ X • h = y , где X - теплицева матрица, составленная из отсчётов входного сигнала. В случ ае двумерной свёртки (1) матрица X блочно теплицева с тепли-цевыми блоками. Положим, что сигналы x и y размера M , а ИХ состоит из N отсчётов, при этом M >> N, где N - нечётно.

Наблюдение выходного сигнала производится неточным образом. Вместо y наблюдают y = y + Ау , где Аy - реализация вектора случайных величин и E(Аyi) = 0, D(Аyi) = ^2 < ^ . Тогда СЛАУ имеет вид y = X • h + Аy, X e RMxN, he RN, y e RM .

Решение СЛАУ (2) h является оценкой решения h точной задачи.

Возмущённая постановка задачи идентификации совпадает с постановкой задачи классического регрессионного анализа [7]. Метод наименьших квадратов (МНК) для задачи (2) позволяет получить оценку h , наилучшую в классе линейных несмещённых оценок, но неустойчивую в случае плохой обусловленности матрицы X , т.е. E^h^ >>|| h ||².

Решение СЛАУ (2) определим, как решение задачи h = inf || h || на множестве Q = { h : Q ( h ) = Q min } , где ^Q min = h mf ^Q ( h ) ^{и Q} ( h ) =| X • h - j y |², ^а |^|| ^{- евк}лидова норма.

Под обусловленностью задачи идентификации будем понимать число обусловленности для задачи псевдообращения матрицы X , в дальнейшем – просто число об условленности матрицы X , определяемо е в [3] как k ₂ ( X ) = || X |I • | X ⁺|| = a , • a N ¹, где a i - сингулярные (или главные) числа матрицы X , а X ⁺ - псев-дообратная матрица Мура-Пенро уза. Также отметим, что матрица X имеет полный столбцовый ранг равный N и k ₂ ( X ) < ^ .

При больших размерностях СЛАУ использование прямы х методов может быть затруднительно по причине ограничения на доступную оперативную память ЭВМ. В этом случае оказывается эффективным применени е различных итерационных методов, одно из преимуществ которых – возможность учёта нелинейных ограничений искомого решения.

Однако в случае плохой обусловленности матрицы СЛАУ большинство итерационных методов [8] имеют медленную сходимость. Более того, при наличии возмущений вектора правой части предельная точка итераций часто сколь угодно далека от искомого решения.

2.    Номер останова как параметр регуляризации

Типичным поведением итерационного приближения является убывание н евязки реш ения, при этом ошибка, начиная с некоторого n_opt , неограниченно растёт. Общей проблемой применения итерационных методов для решения возмущённых СЛАУ является выбор номера останова, близкого к n_opt , позволяющего обеспечить вычислительную устойчивость результата.

Далее, в качестве показателя интенсивности возмущений выходного сигнала, будем использовать соотношение шум-сигнал 8 = D ( А у ) • D ( у ) ^{- 1} • 100% .

На рис. 1 показаны результаты идентификации ИХ системы при 8 = 0% (рис. 1 а ) и в случае возмущений (рис. 1 б ) при 8 = 3%. Для решения задачи применялся итерационный метод наискорейш его спуска (НС) с критерием останова hir^{1 + 1} - #||< 10^{- 8} . Решение точной задачи (рис. 1 а ) при этом треб ует 1000 итераций. При таком же количестве итераций приводится решение приближенной задачи (рис. 1 б ).

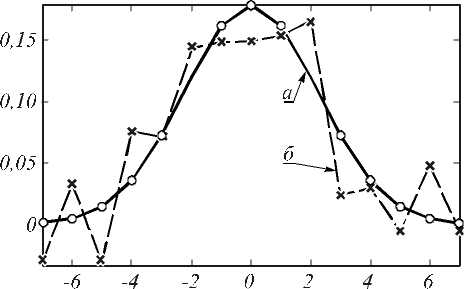
Рис. 1. Решение точной задачи (а) и оценка решения (б) по возмущённым данным

Рассмотрим ошибку решения задачи идентификации

• А( n ) = ||hn) — h\|2,                                        (3)

где h – псевдорешение СЛАУ (2) при отсутствии возмущений Ау = 0 , а hn) - итерационное приближение на шаге n решения СЛАУ (2). Оптимальным номером останова итераций будем называть величину nopt = arg min А( n) .                              (4)

nE N

Очевидно, что непосредственная минимизация функц ионала (3) невозможна ввид у отсутствия априорной информации о А у . Необходимое условие [5] того, чтобы итерационный алгоритм обладал свойством регуляризации, имеет вид

/€ n^opt ) - h

^ 0, при ||А у || ^ 0 .

Рассмотрим регуляризованную систему нормальных уравнений для СЛАУ (2)

( X T • X + «• I ) • h _a = X T • у , aE ( 0, +^ ] , (6) где a - параметр регуляризации, а I - единичная матрица размера N . Тогда с использованием принципа невязки [6] можно установить связь между параметром регуляризации a и номером останова итераций n

I x • < — у ||=| X • h ⁿ ) - у || . (7)

При этом малые номера останова n соответствуют крайне большим значениям параметра a и наоборот.

3.    Оценивание номера оптимальной итерации на основе функции перекрёстной значимости

В работе [5] предлагается оценивать оптимальный номер останова итераций на основе ф ункци и перекрёстной значимости (cross-validation method) [9]. Данный метод выбора параметра a не требует априорной информации о возмущениях в задаче. Суть состоит в ми нимизации ф унк ционала

—2

1                                             1                                          2

V ^(a) = м i ^{1 —} A ^(a)) ^ ^у "• м^{ттсе ( 1 —} A ^{(a)) (8)}

по параметру a .

В формуле (8) A ( a ) = X • ( X T • X + a E ) • X T . Очевидно, что минимизация V ( a ) связана с большим количеством затрат вычислительных ресурсов ЭВМ.

Рассмотрим алгоритм НС, последовательность приближений € ⁿ ) которого определяется соотношениями

€ ^{n + 1 )} = h ⁿ ) — в _n • g ^{( n} ) , g ^{( n} ) = — X T • ( у — X • h ⁿ > ) , (9)

в n =|| g ^{( n} )||2-|| X • g ^{( n} f² . (10)

Необходимо отметить, что у этого метода есть серьёзный недостаток – при нахождении каждого след ующего приближения т реб уется две трудоёмкие операции умножения. В [8] показан приём того, как можно избежать двукратного умножения.

Подобно [5] через e ^{( n} ) = у — X • h € ⁿ ) обозначим вектор невязки и введём матрицу невязки E ^{( n} ) е R^{m х м} , позволяющую выразить вектор невязки в виде е ^{( n} ) = E ^{( n} ) • у . Показано, что для алгоритма наискорейшего спуска матрица невязки представима в виде

E ⁽ n ^{+ 1 )} = ( I -p n - X - X T ) - E ⁽ n > .                    (11)

В итоге, для итерационных алгоритмов ф унк- ционал (8) имеет вид

U ⁽ n ) = M -I E" ^y 2 - MTrace ( E "' )   .

В [5] значение nU = arg min U (n) рассматривает-n ся как оценка оптимального номера останова nopt .

• 4.    Оценивание номера оптимальной итерации на основе регуляризованного решения

с несмещённым квадратом длины

В работе [10] указывается, что среднеквад рати- ческая погрешность E

вызывается смещени-

ем квадрата длины, т.е. величиной E||h -||h||2 и рассматривается класс оценок с несмещённым квад- ратом длины

Неравенство

E [ Q ... ] = ( ^M - N Н' <  f [ Q ( h ) ] =     (13)

= E[Q(X+ -y)] = M -§", показывает, что использование МНК приводит к «дефекту» средней величины суммы квадратов невязок. В результате естественно определить регуляризованные оценки € для которых E [ Q (h)] = M -^". С целью устранения этого дефекта в [10] предлагается определять регуляризованные оценки из совместного решения уравнений (6) и

Q ( h ) = Q min +Y .

Параметр у предлагается выбирать как

Y = N - ( M - N ) ^-1 - Q min .

Очень просто реализовать решение уравнений (6) и (14) с использованием итерационных методов, основываясь на том факте, что при n ^ ^, Q(hn))^Qmin. В итоге, оценка оптимального но мера останова имеет вид ny = arg min (Q (hn)) + y) •

• 5.    Обсуждение численных методов

Вычисление n _y не требует априорной информации об искажающей системе, однако необходимо предварительно вычислить величину Q _min , что эквивалентно решению СЛАУ (2). Формально

Q min = ||( X ■ X ⁺ - 1 ) - у| f = ( M - N K.         (16)

Выражение (16) указывает способ вычисления Qmin . В случае, если информация о дисперсии возму- щений вектора правой части отсутствует, то значение (16) можно вычислить различными методами из [11].

В данной работе величина Q _min вычисляется простым образом – с использованием определения псев-дообратной матрицы X ⁺ = X T - ( X - X T ) . Необходимо отметить, что для вычисления псевдообратных матриц разработаны алгоритмы Гревилля и БенИзраэля, описание которых дано в [3]. В задаче идентификации искажающих систем часто необходимо определить дисперсию аддитивной шумовой составляющей. Выражение (16) позволяет точно определить ^ " при известных входном и выходном сигналах.

Рассмотрим СЛАУ (6), где вместо единичной матрицы I используется некоторая положительно определённая матриц а S

( X T - X + a- 5 ) - h _a X T -у , ае ( 0, +- ] .       (17)

В случае (17) методы, описанные в разделах 3 и 4, оказываются инвариантными относительно выбора матрицы S . Последнее не позволяет рассматривать номер останова, как параметр регуляризации задачи идентификации, связанный с a соотношением (7).

Запишем разложение Холецкого матрицы 5 = R ^T - R , где R - верхнетреугольная матрица. Тогда СЛАУ (17) можно привести к каноническому виду с единичной матрицей след ующим образом

( X T - X +а- R T - R ) -^€ _а = X T - у ,

R ^{- T} - ( X ^T - X +а- R ^T - R ) - h a = R ^{- T} - X T-y ^

^ ( R ^{- T} - X T - X +a- R ) - h a = R ^{- T} - X T - y ^

^ ( R ^{- T} X T^T X - R - ^{- 1} +a- 1 ) - R - h a = R ^{- T} - X ^T - y .

Введём обозначение X - R ¹ = X и R - h a = zt, тогда решение СЛАУ (17) эквивалентно последовательному решению СЛАУ

( X T - X +a- 1 ) - € _a = X ^T - y                   (18)

и

R -^€ a = € a .                                         (19)

При этом решение СЛАУ (18) предлагается искать итерационными методами с оценкой оптимального номера останова итераций n U или n _y . Полученное решение z^n ) корректируется до ^€^ n ) СЛАУ (19) с верхнетреугольной матрицей R .

Этап решения уравнения (19) может включать учёт априорной информации о ИХ искажающей системы. Если известно, что ИХ неотрицательна, то решение (19) необходимо искать в смысле МНК с ограничением на неотрицательность. Соответствующий метод NLSQ описан в [11]. Переопределение СЛАУ (19) единичной строкой позволит учесть нормировку искомой оценки. Таким образом, появляется возможность учёта различных нелинейных ограничений не только в ходе итерационного про- цесса, но, что предпочтительней, – после его окончания. Отметим, что переход от матрицы X к матрице X определяет детерминированное предыскажение в ходного сигнала x .

6.    Выбор стабилизирующего функционала

Под регуляриз ированным решением СЛАУ (17) понимается

€ = arg min ‘ e R N

(I | x . ‘ - j?| 12+«•

II S . ‘ l² ) ,

где последнее слагаемое называют стабилизирующим функционалом [6,12], который определяет матрица S . Авторы предлагают выбрать в качестве матрицы S дискретный аналог дифференцирующего оператора S_diff . Для одномерных сигналов S_diff определяется ленточной матрицей с шириной ленты , равной трём. В случ ае двумерных сигналов предлагается выбрать матрицу S_diff как дискретный ан алог

d[.] d[.j

оператора ——+——, где v 1 и v 2 - переменные по d v 1    d v ₂

перпендикулярным направлениям.

Укажем вид предлагаемой матрицы S_diff для одномерного случая (случай двух координат крайне громоздок)

SdD = diag (-1,—,-1;-1) +diag (3,—,3; 0)+ (20) +diag (-1, —,-1; 1), где diag (a ; i) - обозначает матрицу, у которой на диагонали с номером i расположен вектор a . Известно, что осцилляции восстановленной ИХ преобладают на краях решения, поэтому целесообразно «прижимать» края регуляризованного решения. Для этих целей предлагается использовать S = Sdiff + P, где в одномерном случае матрица P = diag (p,0, — ,0, p; 0), p > 0.

7.    Вычислительные эксперименты идентификации ИХ

Исследование применения на практике рассматриваемых методов приводится как для одномерных, так и для двумерных тестовых сигналов из [13, 14] при 8 , равной 1%, 5%, 10% (рис. 2, 3). Предполагается, что входной сигнал задан точно, то есть возмущения матрицы X отсутств уют. Истинная ИХ искажающей системы изображена на рис. 4.

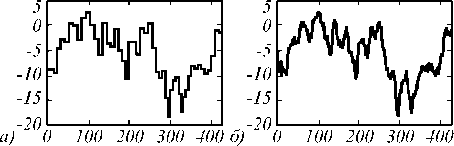
Рис. 2. Тестовые входной (а) и выходной (б) одномерные сигналы. Выходной сигнал для случая 5 = 1%

Рис. 3. Тестовые входное (а) и выходное (б) изображения.

Выходное изображение для случая 5 = 1% . Показано

в инвертированных цветах

Ошибка восстановления ИХ вычисляется по формуле

8 n =| ‘ n )- ‘ |2 .                                     (21)

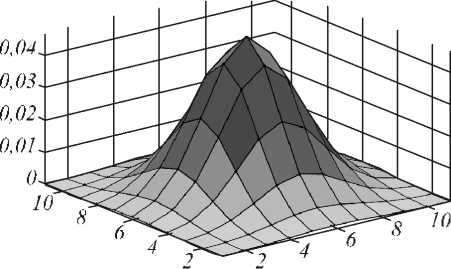
Рис. 4. Истинная гауссообразная ИХ искажающей системы

На рис . 5 изображены восстановленные ИХ при уровне шума 5%.

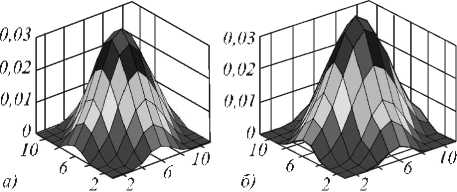
Рис. 5. Восстановленные ИХ для n _Y (а) и n U (б) при уровне шума 5 = 5%

В таблице 1 приводится сравнение качества восстановления ИХ двумя методами, отличающимися оценкой оптимального номера останова итераций.

Оптимальное значение номера останова вычислялось по формуле (4). Обозначения t _Y и t U - время (в секундах), необходимое для восстановления ИХ.

Таблица 1. Показатели качества оценки ИХ по изображениям на рис. 3.

8	n opt	n Y	n U	t Y	t U	8 n Y	8 n u
1%	336	81	179	13	188	0,029	0,026
5%	55	15	41	3	46	0,036	0,033
10%	35	6	23	1,6	28	0,039	0,034

Для одномерной искажающей системы истинная ИХ изображена на рис. 6 а . Восстановленные по сигналам на рис. 2 ИХ для уровня шума 5% приведены на рис. 6 б , в .

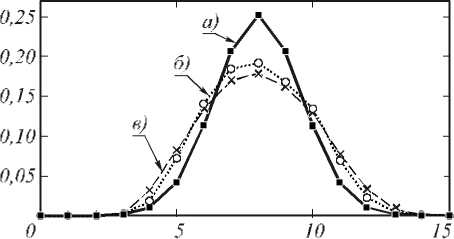
Рис. 6. Истинная ИХ (а), восстановленные ИХ для n_U (б) и n _γ (в) и при уровне шума δ = 5%

В таблице 2 приводится сравнение исслед уемых методов.

Таблица 2. Показатели качества оценки ИХ по тестовым сигналам на рис. 2

δ	n opt	n γ	n U	t γ	t U	ε n γ	ε n U
1	557	156	447	0,09	39	0,076	0,06
5	182	38	173	0,02	15	0,11	0,09
10	79	26	138	0,01	12	0,12	0,10

8.    Обсуждение результатов

Как показывают вычислительные эксперименты, предлагаемый выбор стабилизирующего функционала позволяет существенно уменьшить осцилляции краёв искомого решения. Учёт нелинейного ограничения на неотрицательность ИХ можно было бы осуществлять на каждой итерации метода с использованием проектирования, что не влияет на сходимость метода в принципе, однако изменяет скорость сходимости. Ввиду того, что ограничение нелинейное, провести формальный анализ скорости сходимости метода в этом случае не представляется возможным. В работе ограничение на неотрицат ель-ность ИХ учитывается после завершения итерационного процесса при решении СЛАУ (18). Таким образом, оценка скорости итерационного метода (9)-(10) из [8] остается неизменной.

Результаты, приведенные в таблицах 1 и 2, показывают, что оценка оптимального номера останова nU гораздо ближе к nopt , чем nγ . Однако, вычисление номера nU неэффективно в смысле необходимых затрат ресурсов ЭВМ. Более того, использование nU становится невозможным, начиная с некоторой размерности сигналов. Так при размерности изображения более 64×64 пикселя возникают существенные затруднения при хранении матрицы невязки в оперативной памяти ЭВМ. В этом ключе выгодно отличается оценка nγ , так как не требует громоздких матричных умножений на каждой итерации. Более того, при исполь- зовании номера останова nγ итерационный метод НС может быть записан в спектральной форме, что позволит избежать операций умножения матриц вообще и перейти к умножению спектров подобно алгоритму Ван Циттерта. Коэффициент метода НС βn также может быть вычислен в спектральной области с использованием обычного равенства Парсеваля.

На рис. 7 а приведены графики зависимости величины ε _{n γ} (рис. 7 а , кривая 1) и ε _n (рис. 7 а , кривая 2) от уровня шума δ для задачи идентификации ИХ по сигналам на рис. 2. На рис. 7 б показаны зависимости t _γ ( δ ) (рис. 7 б , кривая 1) и t_U ( δ ) (рис. 7 б, кривая 2), значения указаны в секундах.

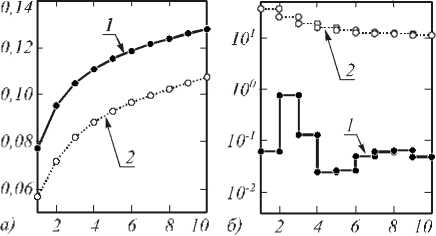
Рис. 7. Зависимость ошибок ε _{n γ} , ε _nU (а) и времени восстановления t _γ , t_U (б) от уровня шума δ

Таким образом, использование оценки оптимального номера останова на основе функции перекрёстной значимости оказывается неприменимым на практике ввид у большого количества затрат ресурсов ЭВМ. Разумный компромисс межд у точностью и ресурсоёмкостью демонстрирует оценка оптимального номера останова n _γ .

Заключение

На практике часто входной сигнал отсутствует или задаётся неточно, при этом в постановке задачи идентификации матрица X становится возмущённой. Для кусочно-постоянных сигналов возможно с определённой точностью по выходному сигналу оценить входной с использованием методов фильтрации, например, [14]. Рассматриваемые алгоритмы могут быть применены и в этом случае, однако вопрос о качестве восстановления остаётся открытым.

Главным преимуществом оценивания оптимального номера останова итераций на основе регуляризованного решения с несмещённым квадратом длины является сущ ествование «быстрого» алгоритма и незначительные требования к объёму оперативной памяти ЭВМ. Предлагаемая работа может иметь развитие в задачах восстановления сигналов при известной модели искажающей системы .

Работа выполнена при поддержке РФФИ (проект № 10-01-00723-а).