Оценка ошибок регрессионных моделей

Y = f(Xi, ... , Xp 31, ... , вm + е, где 31, ..., pm — неизвестные параметры;

е — ошибка аппроксимации У посредством функции регрессии.

В частности, если m = p + 1 и f(Xi, ..., Xp, Po, Pi,..., вp) =

= в о + P 1 X 1 + ... + в p X p , мы имеем модель множественной линейной регрессии

^Y = в о + 3 1 X 1 + ... + в p X p + е.

В этом уравнении некоторые независимые переменные могут быть функциями других переменных или друг друга.

Пусть в = (в₀,..., в ) ^т — вектор параметров размера ( р + 1) х 1, Y = (у, ..., у ) ^т — вектор из n наблюдений, е = ( е 1 , ... , е_п ) ^т — вектор из n ошибок и

X =

x 11

x 12

1    x _{1 n}

x p 1 x p 2

...

x pn

есть ( р + 1) х n — матрица плана. Тогда для модели множественной регрессии имеем

Y=А в + е,             (1)

где е имеет нормальное многомерное распределение N(0, с² • I); I — единичная матрица.

Оценки, которые минимизируют сумму квадратов отклонений

5 = (Y - X • в) • (Y - X • в) , являются (частными) коэффициентами регрессии. Вектор МНК-оценок b = ( b ₀, b 1 ,..., b_p ) ^r получается из решения системы нормальных уравнений

(ХТ • Х)в = ХТ • Y.

Решение этой системы имеет вид

b = (XT • X)-1 (XT • Y)

а его ковариационная матрица равна cov( b ) = о ²( X ^T • X ) ^{- 1}.

Иногда оценку b ₀ называют свободным членом, константой или смещением по Y. Оценка уравнения множественной линейной регрессии (или плоскость наименьших квадратов) может быть записана в виде

Y = X • B или y = b „ + b. • х . + ... + b„ • х„. (2) 0  11     pp

Y — оценочное значение зависимой переменной.

При этом фактическое значение Y = Y + e, где е — вектор ошибок, e е N( 0; о2 • I). При этом если зависимая переменная y £ N(a; 02 • I), то отличие между фактическим значением и его оценкой будет существенно и вектор ошибок e £ N( 0; 02 • I).

В настоящей работе мы попытались рассмотреть эту проблему более подробно.

Пусть распределение из п наблюдений зависимой переменной У не подчиняется нормальному закону распределения.

I. Пусть некоторое подмножество значений (у, ..., у) из множества (у 1 , ..., у ) (п>К) удовлетворяет этому закону.

1) Построим уравнение модели, используя выборку из первых к наблюдений величины У ук) = х к)в + ек), ук) = (У1,..., Ук)г, в = (в0,..., вр)г, ек) = (ер..., ек)т,

	( 1	х11	■ хр1'
Х к =	1	х12	х р2
	1 V	х 1к	х рк 2

Методом наименьших квадратов найдем оценки коэффициентов множественной линейной регрессии

(У^(к) - Х^(к) ■ в) Т ■ (У к - Х^(к) ■ в) ^ min .

Получим вектор коэффициентов: в= ( b ₀,..., b/.

Оценка уравнения имеет вид:

У(к) = Х(к^В иёи

У к = b o + b 1 Xi^k + • • + b p Xp k .

• 2)    Применим полученный вектор коэффициентов В = ( b ₀, ..., b p ) T ко всей выборке объема п, для оценки переменной У:

У(п) = Х(п)В или у(п) = b0 + Ь1Х1п + • + bpxp^, где У(п) = (у,,...,уп), в = (Ь^.Ь/,

	( 1	х11	■ хр1'
Х(п) =	1	х12	•• хр2
	1 V	х 1п	- хрп ,

• 3)    Ошибка аппроксимации У посредством функции регрессии

_е(п) = _У(п) - У ^(п)         (3)

не будет являться нормально распределенной случайной величиной, е ( ^п) g N(0; o ² ■ I) . Проведем ее оценку методом наименьших квадратов:

e(n) = R(t) + e1(n), где              R (t) —тренд;

е1(п) = (е1р е12, ... ,е1п) — вектор оценки остат ков в (3) и е1(п) ^ N(0;o2 ■ I)

• 4)    Окончательно получим:

Y ( ^k) + e ( ^k) = X^(k>B + e^(k),                 выборка

У^(п) + R(t) + e/ⁿ⁾ = X^B + R(t) + e/ⁿ⁾ выборка

• II.    Пусть выборка ( у ..., у_п) не содержит ни одного подмножества значений, распределенных по нормальному закону.

• 1)    Построим уравнение модели, используя всю выборку п наблюдений величины У: у n> = х " р + е ^{( n}\

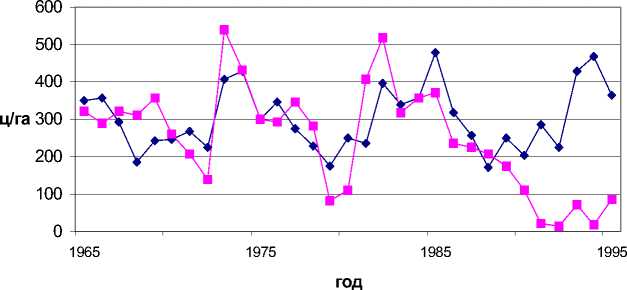
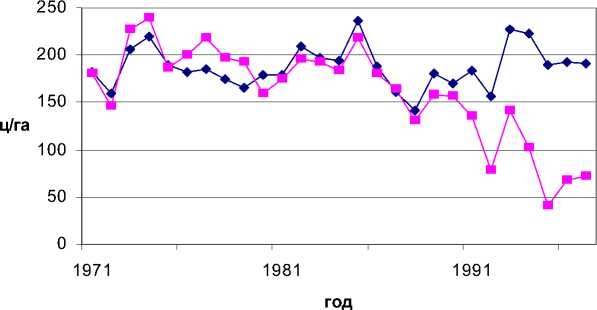
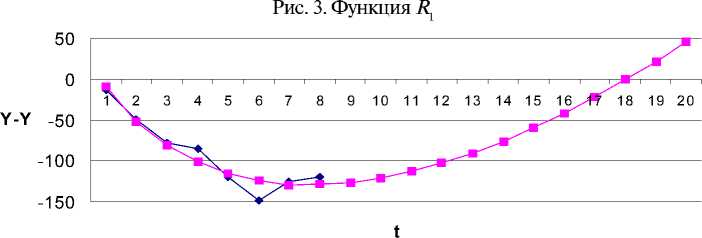
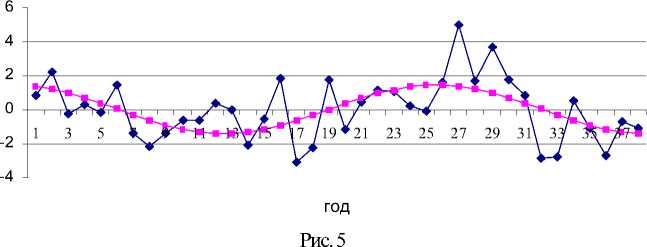
Уn" = (У1, ... , у")', в = (во, ... ,в,)г, е

х11

Х^(п) =

х12

V

х1п

хр1

хр2

хрп J

Методом наименьших квадратов найдем оценки коэффициентов

(У^(п) - Х^(п) ■ в) ■ (У^(п) - Х^(п) ■ в) ^ min.

Получим вектор коэффициентов В = (b ..., b)^T.

Оценка уравнения имеет вид:

У^(п) = Х^(п)В или

У(^П) = bo + Ь1Х1^(п) + • + ЬрХр^(п).

• 2)    Ошибка аппроксимации

е^(п) ^ \(0;^ ■ I), _e(n = Y⁽n) - Y⁽ⁿ⁾.

Проведем ее оценку методом наименьших квадратов е<п) = R(t) + e1(n), тогда е!п) ^ N(0;^2 ■ I).

• 3)    Окончательно получим

Y = Y⁽ⁿ⁾ + R(t) + e1⁽ⁿ⁾ =

= X⁽ⁿ⁾B + R(t) + e1⁽ⁿ⁾ =

= b 0 + b1 x 1⁽ⁿ⁾ + • + bpXpn + R(t) + e1⁽ⁿ⁾.

Рассмотрим применение теории на практических примерах.

Пример 1.

Выпишем математическую модель, описывающую взаимосвязь урожайности томатов с природно-климатическими факторами в условиях Нижнего Поволжья.

⁽У1,-,Ук)

⁽Ук +1,-,Уп)

В данной работе использовались следующие статистические данные:

• -    среднемесячная температура воздуха за год (t1), 1960—2000 гг.;

• -    среднемесячная температура воздуха за теплый период (t2), 1960—2000 гг.;

• -    абсолютный максимум температуры воздуха (Г3), 1960—2000 гг.;

• -    относительная влажность (q), 1960— 2000 гг.;

• -    сумма осадков за год (m1), 1960— 2000 гг.;

• -    сумма осадков за теплый период года (m2), 1960—2000 гг.;

• -    числа Вольфа (W), 1749—2000 гг.;

• -    поток солнечного радиоизлучения на волне 10,7 см (2800 мГц) (R), 1961— 1990 гг.;

• -    количество солнечных вспышек (SW), 1967—1990 гг.;

• -    урожайность томатов на опытной станции ВИР (У1), 1965—2000 гг.;

• -    урожайность томатов в Волгоградской области (У), 1971—2000 гг.

В результате проведенных исследований получены следующие выводы:

• 1.    Распределение чисел Вольфа подчиняется показательному закону с функцией плотности fx) = 0,02е"⁰-^02x(x > 0).

• 2.    Распределение случайных величин t1, t2, t3, m1, m2, q, SW— подчиняется нормальному закону распределения.

• 3.    Выборка урожайности томатов за 1965— 1990 гг. на опытной станции ВИР (за 1971— 1990 гг. в целом по области) подчиняется нормальному закону.

• 4.    Выборка урожайности томатов за 1965— 2000 гг. на опытной станции ВИР (за 1971— 2000 гг. в целом по области) не подчиняется нормальному закону.

В результате анализа получены уравнения для оценки урожайности на ВИР:

У = 1347,65 — 1,4178 • W — 2,6717 • m2 —

• — 23,519 • t3 + 0,138 • t2 • m2,      (4)

в области

• У1 = 488,324 — 0,23 • W— 0,47 • m2 — 6,59 • t3 +

+ 0,016 • t2 • m2.             (5)

При этом для первого уравнения F-отношение F« 5,24 и коэффициент детермина-

Рис. 1. Фактический и оценочный урожай томатов на ВИР (1965—1996 гг.)

Y

Y

Рис. 2. Фактический и оценочный урожай томатов в области (1971—1999 гг.)

Y1

Y1

ции Г = 0,488 (для второго — F® 6,8, Г = 0,63). При уровне значимости а = 0,05 можно говорить о том, что полученная взаимосвязь не случайна.

Как было отмечено ранее, выборка за 1965—2000 гг. из генеральной совокупности, описывающей урожайность томатов, не удовлетворяет нормальному закону распределения. На основании уравнений (3) и (4) построим теоретическую кривую, характеризующую изменчивость урожайности томатов на опытной станции ВИР и в целом по области за 1965—1999 гг. (см. рис. 1 и 2).

Пусть

R (t) = Y (t) - Y (t),              (5‘)

где t = 1 в 1991 г., t = 2 в 1992 г., t = 3 в 1993 г. и т. д.;

Y(t) — фактическая урожайность в Волгоградской области в период времени t;

Y(t) — теоретическое значение урожайности в период времени t, вычисленное при помощи уравнений (3) и (4).

Пусть

R1(t) = a + bt + ct,          (6)

где t e R+, c > 0 для исследуемого периода. Или

R2(t) = a + b • t + c • t • ln(t).       (7)

При этом нам важны те значения параметра t, при которых функция R< 0.

Коэффициенты a, b, c уточним с помощью регрессионного анализа. При этом мы получим дополнительную регрессионную статистику, на основании которой появится возможность уточнить то значение параметра t, при котором R< 0.

R1 = 3,5 • t — 48 • t + 34,        (8)

• -    стандартные ошибки коэффициентов seb = 10,7; set = 7,1; se² = 0,98;

• -    коэффициент детерминации R = 0,94;

• -    стандартная ошибка оценки se_R = 12,7;

• -    F-значение F=40,9;

• -    степени свободы df = 5;

• -    регрессионная сумма квадратов ssreg = 13 272;

• -    остаточная сумма квадратов ss = 809,76.

R2 = 69,6 — 78,52 •t + 25,8 • t• ln(t), (9)

• -    стандартные ошибки коэффициентов se_b= 31,8; set = 21,025; se_tln(t) = 8,7;

• -    коэффициент детерминации R²= 0,93;

• -    стандартная ошибка оценки se_R = 14,5;

• -    F-значение F = 31;

• -    степени свободы df = 5;

• -    регрессионная сумма квадратов ss_reg = 13 032;

• -    остаточная сумма квадратов ss = 1 050,2.

Следуя за определением функции R (см. рис. 3 и 4), найдем такие значения t, при которых R1 и R2 достигают минимума, и R1 = 0, R2 = 0. R1 = 3,5 t²- 48 t + 34, производная R1 = 7t- 48, t ~ 7.

Рис. 4. Функция R2

R = 69,6 — 78,52 • t + 25,8 • t• 1п(0, производная R1‘= -52,72 + 25,8 • ln(t), t« 8.

R1 = 0 при t1 « 0,7 « 1, t₂ « 13;

R2 = 0 при t1 ® 1, t₂® 18.

Окончательно получим следующую модель урожайности томатов в Волгоградской области (при этом е^п ^ N(0;o² • I))

Y + e<^k = X^(kB + e<^k =

Y=

= 488,324 - 0,23 • W - 0,47 • m 2

• -6,59 • t3 + 0,016 • t2 • m 2 + e^(k) , для выборки 1965 - 1990 гг.

У"’ + R( t) + e,⁽ⁿ⁾ = X⁽ⁿ⁾B + R( t) + e,⁽ⁿ⁾ =

= 488,324 - 0,23 • W - 0,47 • m 2 - 6,59 • t3 +

+ 0,016 • t2 • m 2 + 69,6 - 78,52 • t + 25,8 • t• ln(t) + e,⁽ⁿ⁾ для выборки 1991 - 2010гг.

Пример 2.

При построении математической модели прогнозирования урожайности сорго зернового учитывались погодные условия Волгоградской области за последние 50 лет — средняя (t) и максимальная (T) температура воздуха, сумма осадков (m) за теплый период года, числа Вольфа (W — характеристика солнечной активности). Получено уравнение:

Y = 3,24 — 0,03 • m + 0,5 • t —

— 0,00055 • T• m — 0,16 • T + 0,005 • W

При этом коэффициент детерминации г²= 0,42, коэффициент значимости уравнения — 0,01. Однако распределение урожайности сорго зернового подчиняется показательному, но не нормальному закону распределения. Оценим ошибки уравнения при помощи метода наименьших квадратов. Пусть

R (t) = Y (t) - Y (t).

Тогда

R(t) = 0,015 + 1,54 • sin(Пt -1,55) + e1, где t — дата (год) исследования;

е1 — остатки уравнения регрессии, e1^N(0, о^ I).

Тип функции R (t) подбирался по виду кривой остатков (см. рис. 5).