Оценка ожидаемой эффективности инвестиционного проекта в ситуации неопределенности
Автор: Беккер Роман Волдемарович, Кибалов Евгений Борисович
Рубрика: Управление в социально-экономических системах
Статья в выпуске: 2 т.17, 2017 года.
Бесплатный доступ
Анализируется проблема оценки ожидаемой эффективности сооружения мостового перехода в мегаполисе, расположенном на разных берегах крупной равнинной реки. Предлагается подход к решению проблемы на основе применения экономико-математических методов и экспертных технологий, позволяющих определенным образом формализовать и раскрывать различные виды неопределенности, что способствует принятию обоснованных инвестиционных решений. Для решения задач, возникающих в рамках названной проблемы, применяется критерий теории принятия сложных решений Кофмана, аппарат размытых множеств и методика формирования информационной базы расчетов на основе экспертных оценок Ван Вестендорпа. В экспериментальных расчетах, проведенных с помощью разработанной системы моделей на примере предлагаемого к строительству четвертого автодорожного моста через р. Обь в г. Новосибирске, продемонстрированы последствия принятия проектировщиками, инвесторами, строительными подрядчиками и будущими эксплуатантами моста решений, учитывающих не только их коммерческие интересы, но и интересы жителей города - будущих пользователей услугами нового искусственного сооружения.
Ожидаемая эффективность, инвестиционный проект, фактор неопределенности, автодорожный мост, плата за проезд, критерий кофмана, размытые множества, методика ван вестендорпа
Короткий адрес: https://sciup.org/147155179
IDR: 147155179 | УДК: 69 | DOI: 10.14529/ctcr170210
Текст научной статьи Оценка ожидаемой эффективности инвестиционного проекта в ситуации неопределенности
Общим недостатком наиболее часто используемых в традиционных методиках показателей эффективности инвестиционных проектов является предположение о детерминированности входных данных, что приводит к получению смещенных оценок показателей эффективности и риска. Указанное предположение представляется неоправданным упрощением реальности, так как любой инвестиционный проект зависит от множества разнообразных факторов, неоднозначно влияющих на степень его эффективности и рискованности. С одной стороны, принятие обоснованного риска открывает возможность получения различного рода выгод, но, с другой, если риск должным образом не обоснован , появляется возможность потери различного рода ресурсов, недополучения ожидаемого дохода или появления дополнительных расходов в ходе реализации проекта [1].
С учетом сказанного возникает проблема адаптации традиционных методик, регламентирующих оценку экономической эффективности инвестиционных проектов, к ситуациям оценки в условиях объективно существующей неопределенности. Ниже предлагается подход к решению проблемы на основе применения экономико-математических методов и экспертных технологий, позволяющих определенным образом формализовать и раскрывать различные виды неопределенности, что способствует, на наш взгляд, принятию разумных инвестиционных решений.
Существуют различные подходы к учету фактора неопределенности при оценке инвестиционных проектов. Согласно классификации по Найту [2] в зависимости от того, какая информация о состоянии внешней среды доступна в момент принятия решения, различают:
-
– вероятностную (стохастическую) неопределенность;
-
– радикальную (интервальную) неопределенность;
-
– интервально-вероятностную неопределенность.
Понятие вероятностной неопределенности (стохастики) используется в расчетах эффективности, когда «степень возможности» актуализации рассматриваемых сценариев или параметров инвестиционного проекта характеризуется их вероятностями или же, в случае непрерывно меняющихся параметров, – вероятностными распределениями. Использование терминов «случайность», «вероятность» при описании неопределенности, связанной с оценкой эффективности проектов, возможно, когда вероятности отдельных сценариев их реализации точно определены (заранее известны).
В условиях вероятностной неопределенности критерий ожидаемого эффекта, обеспечивающий рациональное экономическое поведение инвесторов, рассчитывается, как показано в [3], по формуле математического ожидания
Эож = УЭkPk , (1) k где Эож – ожидаемый интегральный эффект проекта; Эk – интегральный эффект при k-м сценарии; рk – вероятность актуализации этого сценария.
Использование математического ожидания эффекта в качестве критерия эффективности подвергается критике. Критика связана с тем, что рассчитанный по этой формуле критерий эффективности проекта плохо учитывает риск, генерируемый разбросом эффекта от его среднего значения. Это означает, что одинаковые по своей величине, но противоположные по знаку отклонения при использовании данного способа расчета взаимно погашаются, в то время как для экономического субъекта они могут иметь разную значимость.
Ситуации, когда неопределенность в отношении определения затрат и результатов проекта носит вероятностный характер, а вероятности исчисляются на основе объективной статистики, встречаются в экономике довольно редко. Чаще применяются так называемые субъективные вероятности, под которыми принято понимать вероятности, установленные путем экспертной оценки. Опираясь на объективные или субъективные вероятности отдельных сценариев, экономические субъекты могут принимать решения относительно реализуемых в этих условиях проектов. Соответствующее правило названо критерием Байеса и сформулировано следующим образом: если распределение вероятностей возможных состояний задано дискретно в виде р = [р1, …, рk, …, рn], то в соответствии с данным критерием для вероятности р любое решение (например, j) предпочтительнее другого (например, k) в том случае, если mm
У pa y > У P i a ik , (2) i = 1 i = 1
где a ij – прибыль экономического субъекта, связанная с i -м «состоянием природы» и с j -м решением этого субъекта ( i = 1, …, m ; j = 1, …, n ); p i – вероятность (объективная или субъективная) i -го «состояния природы».
Как было отмечено ранее, при установлении субъективных вероятностей обычно используются экспертные оценки. Однако, как свидетельствуют многочисленные психологические исследования, люди плохо справляются с оценкой вероятностей и, как правило, недооценивают или переоценивают последствия маловероятных сценариев [3].
Радикальная неопределенность возникает в том случае, когда какая бы то ни было информация о вероятностях отдельных сценариев отсутствует (или известно, что реализация любого из этих сценариев вообще не является случайным событием и не может быть охарактеризована в терминах вероятностей). В условиях радикальной неопределенности не существует ни исходной статистической базы для экспертных оценок, ни достаточного числа экспертов, которые могли бы высказать согласованное мнение о вероятностях актуализации отдельных сценариев конкретного инвестиционного проекта. Такая ситуация, характеризующаяся отсутствием статистической устойчивости, вызвана, как правило, уникальностью крупных и сложных инвестиционных проектов.
В условиях радикальной неопределенности «степень возможности актуализации» неопределенных параметров устроена по следующему принципу: все значения параметра в соответствующем интервале считаются возможными («степень возможности актуализации» равна единице), а значения, находящиеся вне этого интервала, – невозможными («степень возможности актуализации» равна нулю). На этом основании данный вид неопределенности называется интервальной. Обычно же об интервальной неопределенности говорят, если об эффекте проекта известно только некоторое (например, дискретное) множество его возможных значений, но не распределение вероятностей на этом множестве.
Управление в социально-экономических системах
Наиболее общая расчетная формула для определения ожидаемого интегрального эффекта инвестиционного проекта в условиях радикальной (интервальной) неопределенности предложена Л. Гурвицем. Она известна под названием «критерий оптимизма-пессимизма». Согласно критерию Гурвица для каждого решения необходимо определить линейную комбинацию минимального (min) и максимального (max) выигрыша и считать наиболее предпочтительным тот проект, для которого эта величина окажется наибольшей:
vH = max i [ a max a i + (1 - a ) min j a ], (3) где ae [0, 1] - коэффициент пессимизма-оптимизма, который принимает значение в зависимости от отношения лица, принимающего решение к риску, от его склонности к оптимизму или к пессимизму.
Помимо рассмотренных выше крайних случаев на практике могут встретиться и промежуточные (смешанные) виды неопределенности, где сочетаются оба рассмотренных вида неопределенности. Для количественной оценки эффективности инвестиционных проектов в условиях интервально-вероятностной неопределенности может быть предложена следующая расчетная формула (см. [3]), обеспечивающая получение экономически корректных результатов. При наличии каких-либо ограничений на вероятности отдельных сценариев или отдельных значений эффекта ( p t ) ожидаемый эффект может быть рассчитан по следующей формуле, которая является своеобразным обобщением формулы Гурвица:
г
г
Эп „ = X • max ож p1,p2 ,...
Е Э iPi +( 1 -х) " min Е Э p?i
V i
p 1 , p 2 ,... ^ i
где максимум и минимум рассчитываются по всем допустимым (удовлетворяющим всем исходным ограничениям) сочетаниям вероятностей отдельных сценариев.
Анализ представленных выше методов количественной оценки эффективности инвестиционных проектов в условиях неопределенности позволяет сделать вывод, что существующие методы ограниченно способны формально описать и учесть всё возможное разнообразие видов неопределенности. Подавляющее большинство методов формализует неопределенности лишь в качестве распределений вероятностей, построенных на основе субъективных экспертных оценок, что в большинстве реальных ситуаций представляется неоправданной идеализацией. Таким образом, в рассмотренных методах неопределенность, независимо от ее природы, отождествляется со случайностью, и это не позволяет учесть всё возможное разнообразие видов неопределенностей, воздействующих на инвестиционный проект.
Использование вероятностного подхода в инвестиционном анализе затрудняется по определенным причинам. К одному из существенных обстоятельств, не позволяющих определить вероятность исхода каждого из предлагаемых вариантов действий путем изучения большого числа случаев, относится уникальность крупномасштабных инвестиционных проектов. Отмеченный факт обуславливает отсутствие возможности свести воедино аналогичные случаи (если таковые вообще существуют) в количестве, достаточном для выработки состоятельного умозаключения по поводу действительной вероятности определенного исхода в заданной ситуации [2].
Кроме того, обычные количественные методы малопригодны для анализа сложных систем, в которых участвует человек, т. е. систем социотехнических. Суть этого принципа можно выразить примерно так: чем сложнее система, тем менее мы способны дать точные и в то же время имеющие практическое значение суждения о ее поведении [4]. Для получения существенных выводов о поведении сложной системы необходимо отказаться от высоких стандартов точности, характерных для простых систем, и привлекать для ее анализа приближенные по своей природе подходы. Одним из таких подходов является теория нечётких множеств, предложенная Л. Заде [4].
Аппарат нечетких множеств широко используется при математическом описании сложных систем в условиях неопределенности, позволяя формализовать знания, представленные в качественной форме, не требуя выполнения предпосылок применимости теории вероятностей. Категория нечёткости и связанные с ней методы важны и по той причине, что с их появлением стало возможно подвергать количественной оценке те явления, которые раньше требовали использования весьма грубых моделей [5, 6].
В настоящей статье мы используем комбинацию методов, опирающихся на теории принятия решений и нечетких множеств. В первом случае неопределенность трактуется нами как риск по Найту [2], во втором случае как приблизительность (расплывчатость) значений независимых и зависимых переменных инвестиционного проекта.
Использование аппарата нечетких множеств предполагает формализацию исходных параметров и целевых показателей эффективности инвестиционного проекта в виде вектора интервальных значений (нечеткого интервала), попадание в каждый интервал которого характеризуется некоторой степенью неопределенности. Данный подход позволяет формализовать и использовать всю доступную неоднородную информацию (детерминированную, интервальную, статистическую, лингвистическую), что повышает достоверность и качество принимаемых стратегических решений относительно конкретного инвестиционного проекта [1]. Далее на конкретном примере показано, как оценка риска неэффективности инвестиционного проекта строительства крупного автодорожного моста через р. Обь (далее – Мост) нами проведена с использованием критериев теории принятия решений и аппарата нечетких множеств.
В качестве критерия оценки эффективности инвестиционного проекта Моста принят стандартный (целевой) для существующих методик показатель чистого дисконтированного дохода (NPV), рассчитываемый по следующей формуле и представляющий собой разницу между суммой денежных поступлений и суммой всех затрат, порождаемых реализацией проекта, дисконтированных (приведенных) к началу проекта:
nn
NPV = -У — t— + V-- t— ,
Z1(1 + r) t £(1 + r) t где It – инвестиционные затраты в период t; CFt – поступления денежных средств в период t; r – ставка дисконтирования; n – количество временных периодов t.
В силу того, что точный объем необходимых инвестиций, эксплуатационных затрат, а также доход от платы за проезд по Мосту точно неизвестны (имеет место фактор неопределенности в определении прогнозных значений данных показателей), проведем оценку риска рассматриваемого инвестиционного проекта в терминах размытых множеств. При формализации проблемы оценки будем следовать Недосекину [7], а в части прогнозных значений экономических показателей опираться на первоисточники1.
В случае интересующего нас Моста значение NPV инвестиционного проекта будет являться нечетким числом (NPV = (NPVmin, NPVmax)), так как нечеткий вид (в соответствии с первоисточниками) имеют показатели в правой части формулы (5):
-
– значение общего объема затрат инвестора на строительство и содержание объекта в течение жизненного цикла проекта по предположению колеблется между 40 и 50 млрд руб.
-
– ожидаемый доход от платы за проезд за весь срок эксплуатации объекта в зависимости от трафика может составить 47,9 млрд руб. при загрузке Моста, равной 86 тыс. автомобилям в сутки, и 14,4 млрд руб., если загрузка составляет 30 % от указанной.
NPV = — (40; 50) + (14,4; 47,9) ^
NPV min = –50 + 14,4 = –35,6 млрд руб.;
NPV max = –40 + 47,9 = 7,9 млрд руб.
В качестве граничного условия эффективности рассматриваемого проекта ( G ) принято значение G = 0. Это означает, что проект будет считаться неэффективным, если суммарное значение дохода от сбора платы по Мосту за весь жизненный цикл проекта не покроет вложенных инвестором в данный проект денежных средств.
Для оценки риска неэффективности проекта строительства Моста, воспользуемся формулой из [7], позволяющей найти степень риска (φ) в случае интервально заданного значения NPV и точечно заданного граничного условия эффективности ( G ):
Управление в социально-экономических системах
' 0,
G - NPV 1 NPV 2 - NPV 1 , 1
при G < NPV 1 ;
при NPV 1 < G < NPV 2 ;
при G > NPV 2 .
Подставив в формулу (6) значения показателей рассматриваемого проекта, получим
0 - ( - 35,6)
35,6
43,5
= 0,818.
Ф =---------
7,9 - ( - 35,6)
Таким образом, риск неэффективности данного проекта составляет 0,818.
Как видно из формулы (6), значение φ находится в диапазоне [0; 1], где 0 означает, что риск неэффективности проекта отсутствует, а степень риска, равная единице означает, что инвестиции окажутся неэффективными и, следовательно, риск убыточности проекта строительства Моста 0,818, выявленный нашим расчетом, очень высок.
Углубим наш анализ, имея ввиду, что значение граничного параметра G , как следует из вышесказанного, критически зависит от суммарного значения дохода от сбора платы по Мосту за весь жизненный цикл проекта. В проектной документации Моста [10] приведена интенсивность движения транспорта по проектируемому объекту при различных (прогнозируемых) значениях тарифных ставок за проезд. Опираясь на эти данные, определим наиболее предпочтительный для инвестора тариф за проезд по Мосту в определенных условиях.
Для сравнения представленных в проектной документации тарифов и выбора более предпочтительного из них воспользуемся критерием Кофмана [12]. Наиболее предпочтительная стратегия из числа допустимых по данному критерию определяется исходя из следующего условия si > sj, если a qt + p q0 + уq+ > aqj + pq 0 + уq+ ,
где si и s j – в нашем случае тарифные стратегии (далее – Тарифы) при их попарном сравнении;
P = 1 -a-у ;(8)
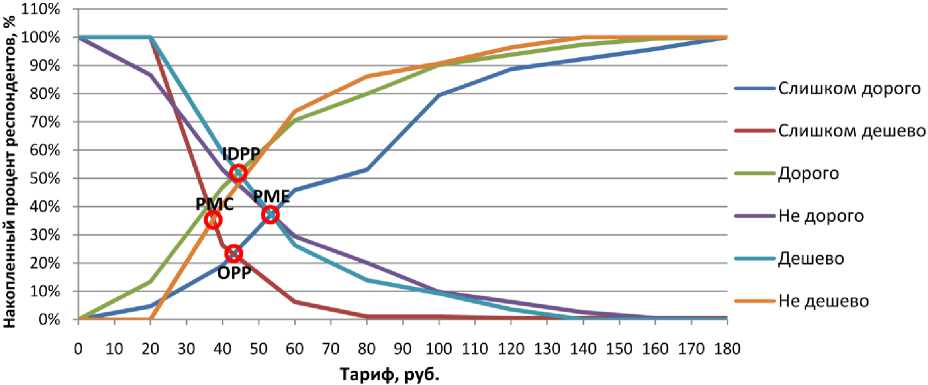
q- = Mr {akr Iakr qk = Mr {akr I Pi < akr < p2}; q+= Mr {akr I akr > P 2 }, где M - средний выигрыш, полученный на подмножестве сценариев qk , определяемый по следующей формуле при наличии нескольких значений akr, удовлетворяющих условию akr < p1: q- = £ akr • gr, r Gqk где gr – возможность актуализации сценария. Средние значения выигрыша, полученного на подмножестве сценариев q0 и q"+ , определяются аналогично. В приведенном критерии результат меньший, чем р1, объявляется «неудачей», а больший, чем р2, оценивается как «успех». Возможность актуализации неудачи оценивается как α·100 %, а успеха – γ·100 %. Все параметры субъективные. Как указано в проектной документации, тарифы за проезд по Мосту будут дифференцированы по категориям транспорта. Как видно из табл. 1, с целью определения тарифных ставок для 1, 2, 3 и 4 категорий транспортных средств (ТС) установлены повышающие коэффициенты, на которые умножается базовая ставка: для 1 категории ТС повышающий коэффициент равен 1, для 2 категории – 1,5, для 3 категории – 2 и для 4 категории – 3. Поэтому далее будет определяться наиболее предпочтительная для инвестора базовая тарифная ставка. Таблица 1 Тарифный план для различных категорий транспортных средств Тарифная группа Категория транспорта Тариф, руб./проезд 1 Легковые автомобили, мотоциклы 50 70 100 2 Грузовые ТС от 2 до 8 т 75 105 150 3 Грузовые ТС от 8 до 14 т 100 140 200 4 Грузовые ТС, автопоезда более 14 т 150 210 300 Представленная в проекте Моста суммарная интенсивность движения по нему всех категорий транспорта на расчётный срок (20 лет) – период n (см. (5)) за вычетом срока строительства, выглядит следующим образом (табл. 2). Таблица 2 Среднегодовая суточная интенсивность движения Тариф (базовый) Интенсивность движения, авт./сут 50 88 480 70 80 395 100 68 735 Однако трафик при платном использовании Моста может оказаться существенно ниже установленного в проектной документации. Учет такой возможности требует рассмотрения трех возможных сценариев – пессимистического, базового и оптимистического. В базовом варианте интенсивность движения по Мосту будет, по предположению, соответствовать значениям, приведенным в проектной документации. В пессимистическом сценарии предполагается, что в случае установления базового тарифа в размере 50 руб. трафик может составить 60,4 % от установленного в проекте Моста, при тарифе 70 руб. – 37,1 % от установленного в базовом сценарии, при 100 руб. – 30,7 % от базового сценария2. В оптимистическом сценарии установлено 20%-ное увеличение значений интенсивности движения при каждом из представленных тарифов (см. табл. 2). По итогам социологического опроса, проведенного проектировщиками Моста, было установлено, что около 20 % респондентов считают платную эксплуатацию вообще плохой идеей и, если плата будет установлена, они не станут ездить по новому Мосту вообще. Тем не менее оптимистический сценарий развития соответствует предположению, что после возведения Моста данная категория автомобилистов будет пользоваться новым искусственным сооружением, несмотря на высказанное в ходе социологического опроса негативное мнение. С учетом различных сценариев интенсивность движения всех категорий ТС по проектируемому Мосту в зависимости от установленного тарифа будет выглядеть следующим образом (табл. 3). Таблица 3 Интенсивность движения транспорта по Мосту при различных сценариях Стратегии (тариф, руб.) Сценарии (интенсивность, авт./сут) r1 r2 r3 Пессимистический Базовый Оптимистический s1 50 53 442 88 480 106 176 s2 70 29 827 80 395 96 474 s3 100 21 102 68 735 82 482 Установим степень возможности актуализации каждого из представленных сценариев с использованием аппарата нечётких множеств, а именно с использованием нечёткой лингвистической переменной. Степень возможности актуализации пессимистического сценария в терминах Управление в социально-экономических системах размытых множеств оценивается как высокая, базового сценария – средняя, а оптимистического – низкая. Введем лингвистическую переменную «возможность актуализации сценария» с подмножествами «низкая», «средняя», «высокая». Также введем носитель х – отрезок вещественной оси [0; 1], на котором определим набор функций принадлежности (µ) по всем указанным подмножествам лингвистической переменной «возможность актуализации сценария» (рис. 1). Представленные на рис. 1 функции принадлежности для каждого подмножества являются трапециевидными. Верхнему основанию трапеции соответствует 100%-ная уверенность в принадлежности уровня возможности актуализации сценария выбранному нечеткому подмножеству (проекция верхнего основания трапеции на область определения носителях образует интервал достоверности). По мере удаления от интервала достоверности уверенность в классификации снижается до нуля, что отражают боковые ребра трапеции. Проекция этих ребер на область определения носителя образует два интервала неуверенности. Все остальные интервалы в области определения носителя формируют объединенный интервал недостоверности, отражающий 100%-ную уверенность, что эти уровни не принадлежат данному нечеткому подмножеству. Рис. 1. Функции принадлежности лингвистической переменной «возможность актуализации сценария» С целью применения обозначенных выше подмножеств в критерии Кофмана проведем так называемую свёртку каждого из подмножеств, позволяющую перейти от векторной формы их представления к одномерной. Как показано в [4], по следующей формуле найдем значения подмножеств «низкая», «средняя» и «высокая» (табл. 4): n A = £нi • Xi, (13) i=1 где А – подмножество лингвистической переменной; µi, i = 1, …, n – степень принадлежности элемента xi подмножеству А; xi – носитель нечёткого множества. низкая = 0 · 1 + 0,1 · 1 + 0,2 · 1 + 0,3 · 0,5 + 0,4 · 0 = 0,45; средняя = 0,2·0 + 0,3·0,5 + 0,4· 1 + 0,5· 1 + 0,6· 1 + 0,7·0,5 + 0,8·0 = 2; высокая = 0,6·0 + 0,7·0,5 + 0,8· 1 + 0,9· 1 + 1 · 1 = 3,05. Критерий Кофмана предполагает использование нормированных значений возможности актуализации сценариев, поэтому для дальнейших вычислений пронормируем полученные значения подмножеств по формуле Wt= . (14) Z Ri i=1 Таблица 4 Нормированные значения подмножеств лингвистической переменной Подмножества Расчётные значения (Ri) Нормированные значения (Wi) Низкая 0,45 0,082 Средняя 2 0,364 Высокая 3,05 0,554 ∑ 5,5 1 Далее определялся доход инвестора за 20 лет эксплуатации моста при указанной выше интенсивности движения в разрезе трех сценариев развития транспортной ситуации. Согласно расчетам проектировщиков при трафике в 86 047 автомобилей в сутки годовой доход от сбора платы прогнозируется в объеме 4292 млн руб. при базовой тарифной ставке, равной 100 руб. Поделив указанное значение годового дохода (4292 млн руб.) на 86 047 проезжающих по мосту автомобилей в сутки, получим прогнозируемый годовой доход, который в среднем планируется получать с одного проезжающего по Мосту автомобиля в сутки. Он оказывается равным 0,05 млн руб. при тарифе в 100 руб. Соответственно, при тарифе 70 руб. доход с одного проезжающего по Мосту автомобиля составит 0,035 млн руб. при тарифе 50 руб. – 0,025 млн руб. Умножив полученные значения на интенсивность движения и на количество лет (20) эксплуатации Моста (период n за вычетом продолжительности строительства), получим прогнозируемый доход инвестора при различных базовых тарифных ставках за проезд и различных сценариях (табл. 5). В пессимистическом сценарии расчёт дохода выглядит следующим образом: – при тарифе 50 руб.: 0,025 · 53 442 · 20 = 26 721 млн руб.; – при тарифе 70 руб.: 0,035 · 29 827 · 20 = 20 879 млн руб.; – при тарифе 100 руб.: 0,05 · 21 102 · 20 = 21 102 млн руб. Для базового и оптимистического сценария расчет дохода от сбора платы за проезд выполняется аналогичным образом. Таблица 5 Доход инвестора от платы за проезд при различных сценариях Стратегии (тариф, руб.) Годовой доход с 1 авт./сут, млн руб. Сценарии (интенсивность, авт./сут) r1 r2 r3 Пессимистический Базовый Оптимистический s1 50 0,025 26 721 44 240 53 088 s2 70 0,035 20 879 56 277 67 532 s3 100 0,05 21 102 68 735 82 482 На основе данных табл. 5 определим с использованием критерия Кофмана наиболее предпочтительный для инвестора в заданных условиях тариф. Исходя из информации проектировщиков Моста, затраты инвестора на строительство и содержание в течение 20 лет мостового перехода составят 45 399 млн руб. Данное значение будет взято в качестве граничного значения p1, доход ниже которого будет считаться «неудачей». Расчёт среднего выигрыша для каждой стратегии будет определен исходя из условия, что возможность актуализации неудачи α оценивается средней (см. табл. 4). В качестве p2 будет взято значение, отражающее 20%-ную прибыль вложенных инвестором средств, то есть р2 = 45 399· 1,2 = 54 478,8 ≈ 54 479 млн руб. Возможность актуализации успеха γ определена в терминах размытых множеств как низкая. Определим значения qk, qk и qk для каждой стратегии (тарифа) по формуле (12). В дальнейших расчётах значения возможности актуализации сценариев из табл. 4 будут пронормированы по формуле (14) с целью получения в конечном итоге адекватных реальности значений суммарного дохода инвестора за весь срок эксплуатации Моста. Управление в социально-экономических системах Для тарифа 50 рублей: q5-0 = 26 721 • 0,6 + 44 240 • 0,4 = 33 728,6 млн руб. q00 = 53 088 млн руб. Значения, удовлетворяющие условию (11), в данной стратегии отсутствуют. Для тарифа 70 рублей: q7"0= 20 879 млн руб. Для данной стратегии отсутствуют значения, находящиеся в интервале p1< akr< p2. q +0 = 56 277 • 0,82 + 67 532 • 0,18 = 58 302,9 млн руб. Для тарифа 100 рублей: q-00 = 21102 млн руб. Для данной стратегии также отсутствуют значения, удовлетворяющие условию (10). q1+00= 68 735 • 0,82 + 82 482 • 0,18 = 71 209,5 млн руб. Далее для каждой из представленных тарифных стратегий рассчитаем по формуле (7) среднее значение выигрыша с целью дальнейшего сравнения данных тарифов и выбора наиболее предпочтительного из них. Как было упомянуто выше, степень возможности актуализации неудачи α оценивается как средняя, а возможность актуализации успеха γ оценивается как низкая. На основе данного заключения указанным факторам присваиваются значения 0,364 и 0,082 соответственно (см. табл. 4). Тогда по формуле (8) β = 0,554. Указанные значения α, β и γ будут в дальнейших расчетах также пронормированы по формуле (14). Для тарифа 50 руб.: s50 = 0,4 · 33728,6+0,6 · 53088 = 45344,2 млн руб. Для тарифа 70 руб.: s70 = 0,82 · 20879+0,18 · 58302,9 = 27615,3 млн руб. Для тарифа 100 руб.: s100 = 0,82 · 21102+0,18 · 71209,5 =30121,4 млн руб. Таким образом, из представленных расчетов видно, что наиболее предпочтительным в заданных условиях будет базовый тариф в размере 50 руб. Тогда тарифная ставка для 1 категории ТС составит 50 руб., для 2 категории – 75 руб., для 3 и 4 категорий – 100 руб. и 150 руб. соответственно. Полученное суммарное значение дохода инвестора от сбора платы за проезд при базовом тарифе в размере 50 руб. не покрывает ожидаемых затрат на реализацию данного проекта. Ожидаемый доход инвестора, согласно расчётам, полученным при использовании критерия Кофмана, составляет 45 344,2 млн руб., что на 55 млн руб. меньше затрат, предполагаемых проектировщиками Моста. Однако полученный результат является средневзвешенным значением возможных исходов, при котором степень возможности актуализации каждого из сценариев использовалась в качестве весов. Поэтому в данном подходе полученное среднее значение дохода инвестора в значительной степени зависит от заданной для каждого сценария степени возможности актуализации, устанавливаемой субъективно. Для повышения степени достоверности определяемого уровня тарифной платы за проезд по Мосту был проведен поверочный расчет с помощью методики Ван Вестендорпа (van Westendorp PSM – price sensitivity measurement) [13]. В ходе исследования было опрошено 194 респондента, которым задавалось четыре вопроса: А. Как Вы считаете, какая плата за разовый проезд по новому мосту для Вас являлась бы настолько высокой, что Вы не стали бы ездить по нему вообще? Б. Какая плата за поездку по мосту Вам представляется настолько низкой, что имело бы смысл задуматься о его преимуществах перед другими мостами с точки зрения скорости передвижения в часы пик? В. Какая стоимость одной поездки по новому мосту кажется Вам высокой, но при которой Вы считали бы для себя возможным пользоваться этим мостом? Г. Какая сумма разовой оплаты проезда по мосту, с Вашей точки зрения, наиболее приемлема для Вас, и Вы бы выбрали поездку по новому мосту, считая это выгодным для себя? В результате ответов респондентов на представленные вопросы порождаются шесть распределений ответов: А – слишком дорого, Б – слишком дешево, В – дорого, Ва – не дорого (как дополнительное значение к В), Г – дешево, Га – не дешево (как дополнительное значение к Г). Полученные распределения изображены в виде графика на рис. 2. По оси абсцисс отложены значения тарифных ставок, по оси ординат – накопленный процент респондентов – участников опроса. Рис. 2. Распределения ответов респондентов Пересечение кривых «дорого» и «дешево» дают точку безразличия (IDPP – indifference price point) – это тариф, который большинство людей не считает дорогим или дешевым, им безразлично. Точка пересечения кривых «слишком дорого» и «слишком дешево» дает оптимальную величину тарифной ставки (OPP – optimum price point). Это точка, в которой меньше всего людей отказываются от поездки по Мосту из-за его высокого тарифа. Пересечение кривых «слишком дешево» и «не дешево» дает точку предельной дешевизны (PMC – point of marginal cheapness). Пересечение «слишком дорого» и «не дорого» дает точку предельной дороговизны (PME – point of marginal expensiveness). Данный подход определения «ценовых вех» позволил определить границы, между которыми должна находиться тарифная ставка за проезд по Мосту. На основе полученных точек пересечения кривых (см. рис. 2) можно сделать вывод, что тариф за проезд должен быть установлен приблизительно в интервале от 35 руб. (точка PMC) до 55 руб. (точка PME). Также по графику видно, что точка, отражающая оптимальную тарифную ставку (OPP), приближенно равна значению 43 руб., а точка безразличия (IDPP) – 44 руб. Таким образом, полученные по критерию Кофмана и по методике Ван Вестендорпа значения наиболее предпочтительной базовой тарифной ставки находятся в интервале 43–50 руб. В связи с этим можно сделать вывод, что установление инвестором базовой тарифной ставки, близкой к данным значениям, позволит получить максимально возможный (по условиям платежеспособного спроса) доход от сбора платы за проезд по Мосту. Согласно последней информации, Новосибирская область решила взять на себя расходы, связанные с подготовкой стройплощадки, чем существенно снизила предполагаемые проектировщиками затраты инвестора, в том числе на погашение кредитов, а также пересмотрела расходы инвестора, связанные с содержанием Моста в период эксплуатации. Всё это позволит, как предполагают в правительстве области, снизить затраты инвестора почти в 1,8 раза [14]. В таком случае при установлении базовой тарифной ставки в интервале 43–50 руб. суммарное значение дохода инвестора от сбора платы за проезд позволит не только покрыть затраты на реализацию рассматриваемого инвестиционного проекта, но и получить прибыль. Управление в социально-экономических системах Авторы благодарят зав. сектором ИЭОПП СО РАН к.э.н. Горяченко Е.Е. за ценные консультации в процессе написания настоящей статьи.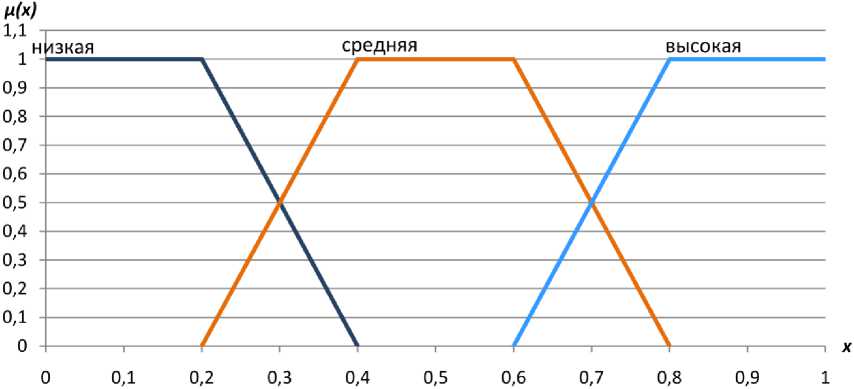
Список литературы Оценка ожидаемой эффективности инвестиционного проекта в ситуации неопределенности
- Деревянко, П.М. Оценка проектов в условиях неопределенности/П.М. Деревянко. -http://www.cfin.ru/finanalysis/invest/fuzzy_analysis.shtml (дата обращения: 03.01.2017).
- Найт, Ф.Х. Риск, неопределенность и прибыль: пер. с англ./Ф.Х. Найт. -М.: Дело, 2003. -360 с.
- Виленский, П.Л. Оценка эффективности инвестиционных проектов. Теория и практика: учеб. пособие/П.Л. Виленский, В.Н. Лившиц, С.А. Смоляк. -2-е изд., перераб. и доп. -М.: Дело, 2002. -888 с.
- Заде, Л. Понятие лингвистической переменной и его применение к принятию приближенный решений/Л. Заде; пер. с англ. Н.И. Ринго; под ред. Н.Н. Моисеева и С.А. Орловского. -М.: Мир, 1976. -167 с.
- Жирабок, А.Н. Нечеткие множества и их использование для принятия решений/А.Н. Жирабок. -http://window.edu.ru/resource/814/20814/files/0102_109.pdf (дата обращения: 08.02.2017).
- Гельруд, Я.Д. Оптимизация развития холдинговой структуры с использованием нечеткой логики/Я.Д. Гельруд//Управление проектами и программами. -2007. -№ 3. -С. 182-190.
- Недосекин, А.О. Оценка риска инвестиций для произвольно-размытых факторов инвестиционного проекта/А.О. Недосекин, А.М. Кокош. -http://www.ifel.ru/br3/5.pdf (дата обращения: 17.12.2016).
- Постановление Правительства Новосибирской области «О заключении концессионного соглашения о строительстве и эксплуатации на платной основе мостового перехода через р. Обь в створе ул. Ипподромской г. Новосибирска» от 2 июня 2016 г. № 159-п (ред. от 14.07.2016). -http://www.invest.nso.ru/ru (дата обращения: 08.01.2017).
- Инвестору четвертого моста в Новосибирске гарантировали доход в 91 млрд//Информационно-аналитическое интернет-издание «Тайга.инфо». -http://tayga.info/news/2016/06/02/~127790/(дата обращения: 09.01.2017).
- Проектная документация мостового перехода через р. Обь в створе ул. Ипподромской г. Новосибирска. Прогноз интенсивности движения с учетом платной эксплуатации мостового перехода. Книга 1.4. -СПб.: АО «Институт «Стройпроект», 2015.
- Титов, С.М. Презентация мостового перехода через р. Обь в створе ул. Ипподромской в г. Новосибирске (Центральный мост) (Москва, 08.12.2015 г.)/С.М. Титов. -М., 2015.
- Хозяйственный риск и методы его измерения: пер. с венг./Т. Бачкаи, Д. Месена, Д. Мико и др. -М.: Экономика, 1979. -184 с.
- Ценовые методы исследования в маркетинге. -http://works.doklad.ru/view/8Na3xqgcFKI/2.html (дата обращения: 26.02.2017).
- Добрались до министров: «После этих дел я по четвертому мосту никогда не проеду»//Информационно-аналитическое интернет-издание «Тайга.инфо». -http://tayga.info/133194 (дата обращения: 21.03.2017).


