Оценка параметров игр с иерархическим вектором интересов

Введение. В играх с иерархическим вектором интересов [1, 2] предполагается, что n игроков образуют сообщество, которое разбивается на группы. Считается, что само сообщество - группа нулевого уровня S 0. Она разбивается на группы первого уровня, каждая из которых, в свою очередь, разбивается на группы второго уровня и т.д. Sj - множество номеров игроков, входящих в группу j уровня k. Последний m -й уровень, образуют группы, каждая из которых состоит только из одного игрока.

В играх этого типа принято, что выигрыши каждого Фго игрока wi зависят от величины выигрыша wj каждой группы Sj, в которую он входит и важности A ^j данной группы для него.

В свою очередь wj зависит от величины ресурсов xl, выделяемых всеми игроками, входящими в группу Sj . Предполагается, что wj монотонно возрастает при увеличении xl для каждого игрока 1. Явный вид функции wj определяется отдельно для каждой прикладной задачи [3].

Таким образом, чем большим ресурсом обладает группа, тем больше выигрыш для входящих в нее игроков.

Однако вопросы о разбиении множества игроков на иерархически организованные группы и оценка важности групп для игроков ранее не рассматривались. Решение этих задач является целью данной работы.

Графовая модель. Очевидно, что объединение игроков в группу может быть вызвано только наличием у них общей цели. Таким образом, каждый игрок может иметь несколько целей, а цели отдельных игроков могут как совпадать, так и различаться [4]. Данная ситуация может быть описана на языке теории графов.

Обозначим через Zk - множество целей игрока k; Z = U ^ ₌₁ Zk - множество целей всех игроков. Построим неориентированный раскрашенный граф G = ( 1,Е,д ), г де I - множество вершин, которые соответствуют игрокам ( | I | = n); E - множество ребер, соединяющих те вершины, которые имеют общие цели; д : E ^ Z - функция такой раскраски ребер, что каждой цели соответствует свой цвет ребра.

В отличие от классического определения клики [5] введем аналогичное определение для раскрашенного графа. Будем называть одноцветной кликой множество попарно смежных вершин, причем смежность определяется ребрами одного цвета. Одноцветная клика называется максимальной, если она не содержится в другой клике с большим количеством вершин.

Попадание игроков в одну группу определяется наличием у них общей цели. Следовательно, указанные игроки соответствуют вершинам графа, объеденным в клики, которые образуют ребра, имеющие цвет, соответствующий данной цели. Весом клики будем называть выигрыш соответствующей группы.

Выигрыш каждого игрока тем больше, чем больше выигрыш групп, в которые он входит. Естественно предположить, что чем больше важность цели для игрока, тем больше ресурс, который он готов выделить для группы, определяемой этой целью, и, следовательно, выигрыш самого игрока.

Обратимся к разработке метода оценки важностей целей и весов клик, определяемых ими.

Оценки важности целей и весов клик. Понятие « важность » является качественным понятием. Для получения количественных оценок качественных показателей может использоваться метод анализа иерархии, предложенный Томасом Саати [6].

Суть метода состоит в следующем. На основе попарного сравнения экспертных оценок важности целей игрока строится матрица по следующему правилу.

Шаг 1. Составить матрицу A = ( aij ) следующим образом:

' 1, 3, если цели i и j одинаково важны; если цель i несколько важнее цели j; aij = 5, если цель i существенно важнее цели j 7, если цель i значительно важнее цели j .9, если цель i абсолютно важнее цели j; aij = a-1 •

Шаг 2. Найти собственный вектор x матрицы A = ( aij ), соответствующий ее максимальному собственному значению.

m

Шаг 3. Нормировать вектор x = ( x 0 , ...,x_m ) (то есть получить ^2 xi = 1).

i =0

Координаты вектора x можно рассматривать в качестве коэффициентов важности целей для данного игрока.

Таким образом, описан метод, позволяющий количественно оцепить важности целей для каждого игрока.

В соответствии с ранее сделанным предположением каждый игрок i выделит для группы Sj pec у pc Ak ■ xi , г де xi - общий ресурс игрока г. Следовательно вес одноцветной клики, соответствующей группе Sj может быть о пределен, как wj ( Ak ■ xi ,i E Sj).

Построение иерархически организованных групп. Группы игроков, соответствующих максимальным кликам, имеющим наибольший вес,составляют первый уровень иерархии.

Опишем процедуру формирования иерархической структуры групп игроков. Найдем максимальную одноцветную клику с наибольшим числом вершин, которая будет соответствовать первой группе первого уровня S1. Эту процедуру будем применять к оставшимся вершинам до их исчерпания. Таким образом, будут найдены группы первого уровня иерархии.

Из каждой клики, соответствующей группам первого уровня, исключим определяющие их ребра. К каждой из них в отдельности применим описанную выше процедуру. Тем самым будут определены группы второго уровня иерархии. Процесс продолжается до тех пор, пока все клики не станут одновершинными, что соответствует последнему уровню т.

Численный пример. Пусть множество игроков и их цели описаны графом, приведенном на рис. 1 (различие целей (цветов ребер) показано различием типов линий).

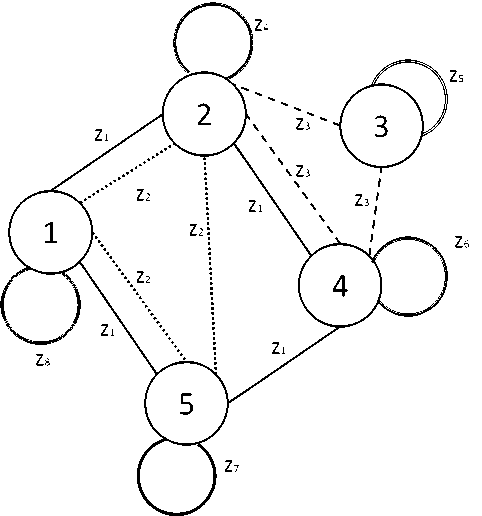
Рис. 1. Неориентированный граф с цветными ребрами, описывающий множество игроков

В результате использования метода получено следующее разбиение сообщества игроков на иерархически упорядоченные группы (рис. 2):

Рис. 2. Иерархическое представление групп субъектов

Заключение. Описанные методы позволяют находить иерархическую структуру групп игроков, позволяющую максимизировать их выигрыши. Кроме того, найденные параметры позволяют использовать теорему Гермейера и Вателя, сформулированную и доказанную в [1], для нахождения равновесия по Нэшу.