Оценка параметров эллиптического контура

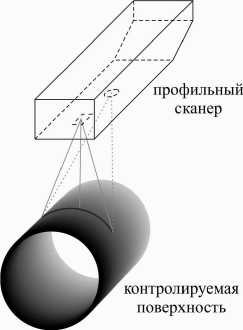
Бесконтактный оптический способ измерения получил широкое распространение в различных технологических процессах и измерительных системах. Оптические устройства применяются для измерения расстояния – либо в виде дальномеров или в виде профильных сканеров, которые позволяют строить 2D контур (профиль).

При производстве труб возникает вопросы контроля диаметра трубы и оценки ее отклонения от номинала. В современном производстве для этих целей используют профильные системы, которые позволяет измерять контур объекта, представляя его в виде совокупности точек (см. рис. 1 а). Измеренный контур трубы, что естественно, будет представлять собой эллипс (см. рис. 1 б).

Задача оценивания параметров эллипса интересна не только с практической, но с научной точки зрения. С точки зрения науки интерес представляет вывод алгоритма оценивания совокупности его параметров (значению полуосей, координат центра эллипса и угла поворота). А практическая значимость работы заключается в применении разработанного способа для автоматизации сбора параметров по контролю качества труб и конических поверхностей.

1. ПОСТАНОВКА ПРОБЛЕМЫ

Исследования в этой области, а именно оценивание параметров эллипса, проводилось в основном зарубежными авторами [1]-[7]. Основополагающей работой является [1], в которой автором предложен следующий подход: уравнение эллипса записывается в форме:

F ( a, x ) = a • x = ax ² + bxy +

+ cy ² + dx + ey + f = 0

, где a = [a b c d e f ]T, x = [x2 xy y2 x y 1]T

Проводится минимизация выражения

N

D ( a ) = Z F ( x i ) 2

i = 1

, при котором выполняется условие a2 + 0,5b2 + c2 = 1 (алгебраическая инва-риантная константа, верная для уравнения эллипса). После нахождения коэффициентов [a b c d e f ], определяются канонические параметры эллипса – величина большой и малой полуоси, угол поворота и координаты центра.

В работах [2]-[7] алгоритмы строятся аналогичным образом, с той лишь разницей, что выбираются другие инварианты.

В данной статье предлагается новый способ к решению указанной проблемы. Он отличается более общим методологическим подходом при выводе алгоритма оценивания параметров, не предполагает наличие инвариантов и использует только аналитические уравнения, описывающие контур.

Основная идея заключалась в оценке параметров эллипса с помощью итерационных методов решения нелинейных уравнений, содержащие функции синуса и косинуса. Эта идея была подсказана устройством фазовой автоподстройки частоты (ФАПЧ). В частности, похожий прием был использован в работе [8] для оценивания параметров компенсатора искажений квадратурного амплитудного модулированного сигнала (КАМ-сигнала). Представленная работа является продолжением работы [9] и [10], где были ис-

a

Рис. 1. К задаче оценивания параметров эллипса

б

пользованы похожие приемы для оценивания параметров контура на плоскости.

Эллиптические контуры представляют собой линии второго порядка – окружности и эллипсы, которые описываются уравнением вида:

xz

-у + . = 1 .

a ² b ²

В ходе измерений производится оценка параметров контура, по которым определяется качество его изготовления – отклонение от номинальных параметров и дефекты изготовления.

Преобразование, связывающее между собой координаты эллипса ( x , z ) (см. формулу 1) и координаты контура, получаемого в профильной системе ( xs , zs ), имеет вид:

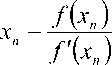
– решение системы нелинейных уравнение методом простой итерации, которая сводится к следующему: для системы уравнений x — f (x, z ) = 0

• <             , итерационное решение -

• . z - g (x, z ) = 0
3.    АЛГОРИТМ ОЦЕНИВАНИЯ КООРДИНАТ ЦЕНТРА ЭЛЛИПСА

x n + 1 = ^f ( x n , z n )> z n + 1 = g ( x n , z n ) .

Для вывода алгоритма оценки координат его центра будет использовано уравнение окружности с центром в точке ( X , Z ):

( xs - X ) ² + ( zs - Z ) ² = R² ,         (3)

где xs , zs – координаты точек контура, R – радиус.

В уравнении (3) присутствует три неизвестных – R , X , Z , которые необходимо оценить.

Для решения использовался метод наименьших квадратов, и для этого была использована функция, которую необходимо минимизировать:

f ( X, Z, R ) = ^ [ ( xS i - X ) ² + ( zS i - Z ) ² - R ² ] 2 ^ min , ⁽4) i = 1

где xs_i , zs_i – координаты точек контура, N – количество точек контура.

Наиболее очевидный способ поиска минимума функции – это нахождения частных производных по искомым переменным и сведения его к системе нелинейных уравнений. Однако это способ не дал практических результатов – итерационный способ решения уравнения приводит к некорректным результатам (не выполняется условие сходимости).

Вместо этого использовался следующий прием.

При фиксированном значении R=r можно оценить параметры X , Z :

N ₂

f ( X , Z ) = У [ ( xs i - X ) + ( zs i - Z ) - r 2 ] ^ min, (5)

i = 1

Решение определяется системой нелинейных уравнений, найденных путем дифференцирования выражение (5) по параметрам ( X , Z ) :

' A ₂ • X ³ + B ₂ • X ² + C ₂ • X + D ₂ = 0;

_A3 • Z ³ + B 3 • Z ² + C 3 • Z + D 3 = 0.

где A2 = 4N, B2 =-12•^Txsi, i=1

N

C = y {12 • xs ²

2i i=1

- 4 • r ² + 4 ( Z - zs_t ) ² } ,

N ₂ D₂ = У { - 4 • xs , ( xs ² - r ² + ( Z - 2Sj )² 2 iii

= 1

N

A. = 4 N B, =-12•¥ zs - 33 i

,                             i = 1           ,

N

C 3 = Ev ² • zs i ² - 4 • r ² + 4 ( X - zs i ) ²}.

i = 1

N

D₃ = У {- 4 • zs ,. ( zs ²

3        ii i=1

- r ²+ ( X

- xs i ) л.

N – количество точек в контуре (профиле).

Итерационное решение имеет вид:

X

n + 1

A 2 • X n + B 2 • X 2 + D 2

C 2

Z

n + 1

A 3 • Z n + B 3 • Z n + D 3

C 3

• 1.    Выбираем первоначальные значения X₀,Z₀,R₀и n=0.

• 2.    Определяем X_n+1,Z_n+1при r = R_n по формуле (8).

• 3.    Вычислить f (Rn), f'(Rn) при x0 = X_n+1, z0 = Z_n+1по формулам (8) и (11).

• 4.    Вычислить f (Rn + 5), f'(R_n + 5) при x0 = X_n+1, z0 = Z_n+1по формулам (8) и (11).

• 5.    Вычислить Rn₊₁по формуле (10).

• 6.    n = n + 1 и перейти к шагу №2.

4.    ТОЧНАЯ ОЦЕНКА ПАРАМЕТРОВ

Переходов от шага №6 к шагу №2 определяет количество итераций алгоритма – n .

На выходе работы алгоритма имеется грубая оценка параметров, который обозначим как ( X ', Z ' ) .

Зная оценку координат центра ( X ', Z ') , можно оценить параметры - a , b , р . Для этого рассчитывается расстояние от ( X ', Z ') до точек контура ( xs i , zs i ) и угол, который формируют прямые, проходящие через ( X ', Z ') и ( xs i , zs i ) :

r=7( xsi - X)2+(zsi - Z)2, ai = atan2 ((zsi - Z), (xsi - X))          .(12)

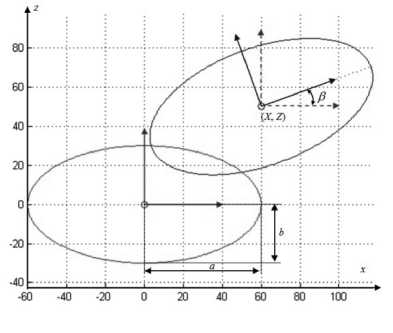
Максимальное значение max ( r ) будет являться грубой оценкой параметра a ' , минимальное значение min ( r i ) - b' . В направлении, где r. достигает своего максимума, будет определять угол поворота в . Для подтверждения этого вывода на рис. 2 представлена геометрическая иллюстрация.

При фиксированном значении X = x 0, Z = z 0 можно оценить параметр R :

N ₂ f ( R ) = У [ ( xs i - x0 ) + ( zs i - z 0 )² - R ² ] ^ min .(8) i = 1

Решать уравнение (9) будем искать в следующем виде:

q ( R ) = f ( R ) - f ( R + 5 ) » 0 ,     (9)

где 5 - малая величина (в расчетах было использовано 5 = 10 - 6 ).

Тогда

Последний этап – это точное оценивание параметров - a , b , X , Z , в . На этом этапе одновременно используется поиск по сетке (фиксируется значения параметров a , b ), также итерационная процедура - по параметрам X , Z , в .

R

n + 1

= R n

q (Rn)

q'(Rn)

= R n

f (R)-f(R+5) (10) f ■( R)-f'(R + 6)’ (10)

N f ‘(R ) = -4 R •УК xsi i=1

^{- x 0 ) 2 +( zs} i ^{- z 0 ) 2 - R 2} } ,(11)

Объединяем описанные выражения в единую процедуру оптимизации. Алгоритм имеет следующий вид:

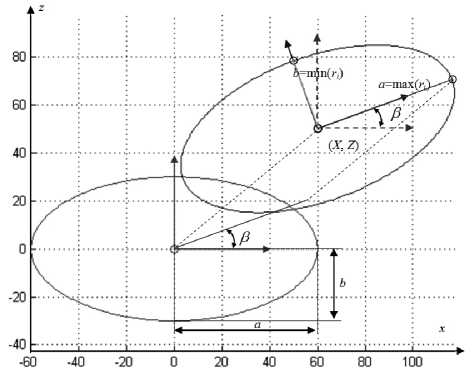
Рис. 2. К оценке параметров величины полуосей и угла поворота

Преобразуем координаты ( xs . , zs i ) в ( xs 1 i , zs1 i ) согласно найденным в , ( X ', Z ' ) :

' xs 1 .?		^ cos ( e ')	- sin ( e ')	0"	- 1
zs 1 i	=	sin ( e ')	cos ( e ')	0	X
I1 J		I 0	0	1,

' A • A e ⁷ + B₁ • A e ⁶ + C _VA^ + D 1 • A e ⁴ + + E₁ •A e ³ + F -ee ² + G1 A^e + H 1 = 0, A, •A X ³ + B, •A X ² + C •A X ¹ + D, = 0, 2222

_ A ₃ • A Z ³ + B ₃ • A Z ² + C ₃ • A Z ¹ + D ₃ = 0.

Итерационное решение имеет вид:

	f1	0	- X ')		f xs
X	0	1	- Z '	X	zsi	.            (13)
	10	0	1 J		I1 J

A e „ + 1

A • Ae ; + B 1 • Ae n + c 1 • а д⁵ + D 1 • Ae⁴ 4 + e 1 • a e n + f • A e n + h 1 G 1

Обозначим как ( A X , A Z ) и A e — поправки к центру эллипса и углу разворота. Координаты точек ( xs 1 . , zs 1 i ) связаны с координатами точек «идеального» контура эллипса ( x i , z i ) через преобразование:

xs = x • cos ( A e ) - z • sin ( А в ) +A X , zs = x • sin ( A e ) + z • cos ( A e ) +A Z .

Тогда:

x = ( xs - X 0 ) • cos ( A e ) + ( zs - A Z ) • sin ( A e ), z = - ( xs - X 0 ) • sin ( A e ) + ( zs -A Z ) • cos ( A e ) (^)

Подставим (15) в выражение (1), получим:

(( xs - X 0 ) • cos ( e ) + ( zs - Z 0 ) • sin ( в )) 2 b ² +

( - ( xs - X 0 ) " sin ( e ) + ( zs - Z 0 )¹ cos ( e )) 2 a 2 - (16)

- a ² b ² = 0

Полагая, что Ae мал (- 5 < Ae < 5 градусов), заменим функции косинуса и синуса на их лине- аризованные выражения:

sin ( A e ) «A e , cos ( A e ) «1 - 0,5A e 2 .

Подставляя (19) в (18) получаем: ( ( xs 1 - A X ) • ( 1 - 0,5 A e ² ) + ( zs1 - A Z ) • A e ) 2 b ² + ( - ( xs l -A X ) • в + ( zsl -A Z ) • cos ( 1 - 0,5 A e ² )) 2 a ² -

- a ² b ² = 0                                        .(18)

При фиксированных значениях a , b , можно найти параметры ( A X ,A Z ) и A e , для этого используем метод наименьших квадратов, минимизирую функцию:

f(AX,AZ,e) = £fexs 1. -AX)'(1 -0,5Ae2)+(zs1. -AZ)• Ae)2b2 + i=1

( - ( xs l . - A X ) • A e + ( zs 1 . - A Z ) • cos ( 1 - 0,5 A e ² )) 2 a ² - a ² b ² }         .(19)

Решение определяется системой нелинейных уравнений, найденных путем дифференцирования выражение (19) по искомым параметрам ( a x , a z , e ) .

После приведения выражений к единому виду, можем записать:

A 2 •A X n + B 2 •A X n ² + D 2

^{A X} n + 1

C ₂

A A 3 • Z n + B 3 •A Z n + D 3

^{A Z}n +1              _r

C ₃

Выражения для коэффициентов A ₁, B ₁ и т.д. в формулах (21) – (22) представляют собой полином с большим числом переменных. Для их вычисления в аналитическом виде целесообразно использовать математические пакеты (например, Matlab, MathCad и т.д.).

Так как в данном алгоритме используется поиск по сетке параметров a , b , то каждому паре этих значений ставится в соответствие вычисленные параметры ( A X , A Z ) , A e и метрика:

N metric =H(( x 1.-AX)• cos(Ae)+(z 1. -AZ)• sin(Ae))2 • b2 +

. = 1

( - ( x 1 . -A X ) • sin ( A e ) + ( z 1 . -A Z ) • cos ( A e )) ² • a ² - a ² b ² }

Таким образом, отыскивая минимум метрики (28), будут оценены параметры a , b . А используя найденные значения ( A X , A Z ) , A e ,определятся параметров X , Z , e , которые связаны через следующую матрицу:

f cos ( e )	- sin ( e )	X )	f cos ( A e )	- sin ( A e )	A X J"1
sin ( e )	cos ( e )	Z =	sin ( A e )	cos ( A e )	A Z   x
I 0	0	1 J	.1    0	0	1 J
f cos ( e ,) -		sm( e ’)	0 у1 f 1	0 - X 'A	- 1
x sin ( e ')    cos ( e ')			0 x 0	1    - Z ‘	. (24)
V	0	0	1 J V 0	0 1 J,

ЗАКЛЮЧЕНИЕ

В статье представлен алгоритм оценивания параметров эллиптического контура: значения полуосей, координат центра и угла поворота. Данная задача была сведена к системе нелинейных уравнений, решаемой итерационным способом. Результаты работы планируется использовать для автоматизации сбора параметров по контролю качества труб и конических поверхностей, конту- ры которых измеряются с помощью профильных систем. Дальнейшие исследования вопросов совмещения и оценки параметров будут связаны со сложными контурами, отдельные части которых описываются различными уравнениями.