Оценка племенной ценности быков-производителей бурой швицкой породы методами множественной линейной регрессии

Введение. Оценка племенной ценности быков-производителей является основополагающим фактором при повышении породности стада и устойчивой передачи потомкам наследственной основы. Современные методы оценки, применяемые, в основном, в странах ближнего и дальнего зарубежья, ориентированы на использование геномной селекции [2]. Основное преимущество данной технологии заключается в возможности получить достоверную информацию о племенных качествах производителей с вероятностью от 60% и более [3, 5]. В условиях активной интенсификации и оптимизации селекционных программ геномная оценка является актуальным и пер-септивным направлением в исследованиях, направленных на повышение рентабельности репродукторов за счет достаточно точной и быстрой оценки животных.

Основными элементами геномной оценки быков-производителей служат специально разработанные племенные индексы, выражаемые в относительных

величинах [4]. В зависимости от страны, где проводился геномный анализ, значения индексов идентифицируются по-разному. Однако основополагающим массивом всегда выступают общая племенная ценность, продуктивность (молочная, мясная) и здоровье животных.

В данной статье была изучена степень взаимосвязи и влияния геномных индексов на общую племенную ценность быков-производителей бурой швиц-кой породы при использовании методов множественной линейной регрессии.

Материалы и методы исследований. Объектом исследований служили быки-производители бурой швицкой породы австрийского происхождения (n=300), рожденные в 2021 году. Данные по бонитировке племенных индексов изучаемых животных представлены на площадке организации «Центральной рабочей группы австрийских животноводов», доступ: Zuchtwert Austria. Методика проведения исследований отражена в таблице 1.

Таблица 1 – Схема исследований

Быки-производители бурой швицкой породы (n=300)
Изучаемые индексы
GZW		MW			FW		FIT
Общая племенная ценность (ОПЦ)		Молочная продуктивность (МП)			Откормочные качества (ОК)		Фитнесс (Ф)
Множественная линейная регрессия (МНА)
Метод Enter			Пошаговый метод
Статистические методы
rP	ANOVA			R2		МНК
Корреляция Пирсона	Дисперсионный анализ			Коэффициент детерминации		Метод наименьших квадратов

В предыдущих исследованиях [1, 2] мы уже подробно останавливались на описательной характеристике изучаемых индексов. В связи с этим в представленной статье будет дана их упрощенная расшифровка. Для удобства восприятия дальнейшее обозначение индексов GZW, MW, FW, FIT представлено следующими аббревиатурами: ОПЦ (общая племенная ценность), МП (молочная продуктивность), ОК (откормочные качества), Ф (фитнесс) соответственно.

Для моделирования взаимосвязи общей племенной ценности (зависимой переменной) с молочной продуктивностью, откормочными качествами и фитнесом (независимыми переменными) использовалась множественная линейная регрессия (МНА). Чтобы вычислить предполагаемые отношения между изучаемыми переменными, использовали два метода: Enter (принудительное) и пошаговое включение. Первый подразумевает введение в регрессионный анализ всех изучаемых предикторов вне зависимости от того, имеют ли они значимое влияние или нет. Пошаговый метод позволил автоматически устранить незначимые предикторы, если таковые не входили в противоречие с логикой изучаемого признака.

Статистические методы включали определение:

корреляций по Пирсону ( rP) – линейной взаимосвяз и, которая принимает значения от -1 до 1; дисперсионный анализ (ANOVA) – оценка влияния факторов на изучаемый признак; коэффициент детерминации ( R²) – теснота связей между факторами регрессии и зависимой переменной; метод наименьших квадратов (МНК-оценка) – способ аппроксимации регрессионной линии, при котором сумма квадратов разностей между наблюдаемыми и предсказанными значениями минимизируется.

Для обработки информационных показателей использовался пакет статистического программного обеспечения BM SPSS Statistics 27.0.1 IF026.

Результаты исследований и их анализ . В первый этап исследований входило изучение корреляционный матрицы индексов с целью определения значимости показателей для дальнейшего анализа (таблица 2). Мультиколлинеарность значимости общей племенной ценности с молочной продуктивностью и фитнесом находилась на достаточно высоком уровне – 0,0005, соответственно к данным показателям применять регрессионную модель нежелательно. Поскольку дальнейший анализ основывался на стандартном методе ( Enter ), применялось принудительной включение всех изучаемых значений.

Таблица 2 – Матрица корреляции

Показатели		ОПЦ	МП	ОК	Ф
Корреляция Пирсона ( rP)	ОПЦ	1,000	0,645	0,122	0,288
	МП	0,645	1,000	0,039	-0,496
	ОК	0,122	0,039	1,000	-0,041
	Ф	0,288	-0,496	-0,041	1,000
p (односторонняя)	ОПЦ	-	0,0005	0,018	0,0005
	МП	0,0005	-	0,250	0,0005
	ОК	0,018	0,250	-	0,241
	Ф	0,0005	0,0005	0,241	-

Примечание: p – значимость

Последующие операции, связанные с построением регрессии по методу Enter , будут обозначаться моделью №1.

В таблице 3 выявлена теснота взаимосвязей дисперсии, где предикторами выступают: (константа), М

П, ОК, Ф; зависимая переменная – ОПЦ. Процедура оценки линейной модели №1 позволила провести интерпретацию данных, которые предложены ниже (таблица 3).

Таблица 3 – Сводка для модели №1

Модель	R	R2	Скорректированный R2	S e	Дарбин-Уотсон
1	0,960	0,921	0,920	1,508	1,868

Примечание: S e – стандартная ошибка оценки

Связь зависимой переменной с совокупностью независимых (R) составила 0,960 или 96%. Коэффициент множественной детерминации (R2) соответственно демонстрирует также высокое значение – 0,921. Таким образом, доля дисперсии переменной отклика составила 92,1% вариаций. Иначе говоря, дисперсия зависимой переменной обусловлена всеми независимыми переменными. Средние расстояния наблюдаемых значений отклоняются от линии регрессии на 1,508. Автокорреляция остатка по Дарбину-Уотсону составила 1,868, что свидетельствует о корректности проведения регрессионного анализа, так как полученное значение входит в интервал от 1,5-2,5.

Таблица 4 – ANOVA для модели №1

Модель		TSS	df	Средний квадрат	F	p
1	Регрессия	7769,322	3	2589,774	1139,072	0,0005
	Остаток	666,159	293	2,274
	Всего	8435,481	296

Примечание: TSS – сумма квадратов; df – степени свободы

Согласно данным таблицы 4, доля дисперсии ОПЦ под влиянием МП, ОК и Ф составила 7769,3, при этом доля без влияния (остаток) – 666,1, что согласуется с полученным коэффициентом множественной детерминации. Достоверность построенной связи при критерии Фишера ( F ) равном 1139 обладала достаточно высокой значимостью – на уровне 0,0005 или 99,9995%.

Перед анализом таблицы 5 внесем ясность для понимания представленных обозначений: т – отношение коэффициента регрессии к стандартной ошибке; SEM – стандартная ошибка, Н/СК – не/стандартизованные коэффициенты. Стоит отметить, что значения стандартизованных коэффициентов достаточно близки к нестандартизированным, то есть имеющиеся данные стремятся к нормальному распределению. Среднее значение переменной ответа (константы) нестандартизированных коэффициентов при равенстве нулю переменных-предикторов составило -76,619. По таблице также видно, что все изучаемые индексы имеют значительный вклад в формирование константы (общей племенной ценности), поскольку значимость для них составила не более 0,0005 или 99,9995%.

Таблица 5 – МНК-оценка параметров квадратичных моделей по методу Enter

Модель	НК		СК	т	p
	B	SEM	Бета
(Константа)	-76,619	3,722		-20,583	0,0005
МП	1,030	0,019	1,043	55,155	0,0005
ОК	0,089	0,013	0,114	6,949	0,0005
Ф	0,686	0,016	0,811	42,859	0,0005

Соответственно уравнение регрессии для модели №1 будет иметь следующий вид:

ОПЦ=-76,619+1,030*(МП)+0,089*(ОК)+0,686*(Ф);

При внесении в формулу средних значений предикторов получаем:

ОПЦ=-76,619+1,030*(130)+0,089*(100)+0,686*(110)= 141,641 .

Основываясь на статистке остатков (таблица 6)   ченных в диапазон минимального и максимального делаем вывод, что регрессионная модель по методу   показателей – 123,51-149,73.

Enter соответствует предсказанным значениям, вклю-

Таблица 6 – Статистика остатков для модели №1

Показатели	Минимум	Максимум	Среднее	SD	n
Предсказанное значение	123,51	149,73	133,15	5,123	297
Остаток	-3,872	4,552	0,0005	1,500	297
Стандартная: Предсказанное значение	-1,882	3,237	0,0005	1,000	297
Стандартная: Остаток	-2,568	3,019	0,0005	0,995	297

Примечание: SD – стандартная отклонения

При построении графиков стандартизированных остатков и нормальности наблюдений (рисунок 1,2) можем отметить отсутствие выбросов и линейно- возрастающую зависимость при получении ожидаемой вероятности.

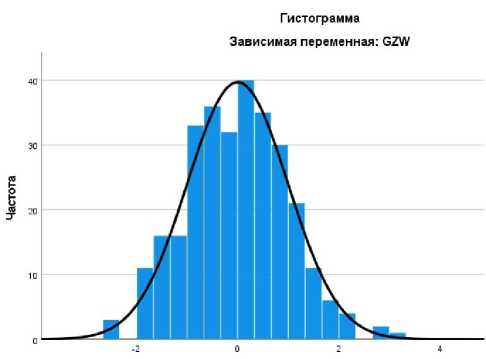
Регрессия Стандартизованный остаток

Рис. 1 – Гистограмма остатков

Нормальный Р-Р график регрессии Стандартизованный остаток

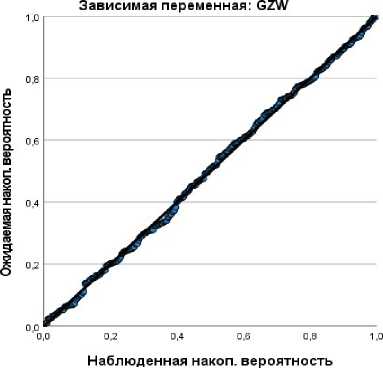
Рис. 2 – Р-Р график наблюдений

Учитывая тот факт, что метод Enter при построении корреляционный матрицы выявил высокий показатель значимости зависимой переменной (ОПЦ) с предикторами (МП и Ф), полученные результаты имеет смысл ставить под сомнение. Для этого воспользуемся пошаговым методом, который устранит неточности или подтвердит корректность проведенного анализа. Поскольку статистика остатков идентична модели №1, а дисперсионный анализ также демонстрирует значимую связь, повторное построение данных таб- лиц мы исключим.

Введенные в пошаговый метод новых моделей соответствует следующим переменным: модель №2 : константа, МП; модель №3 : константа, МП, Ф; зависимая переменная для всех предикторов остается прежней – ОПЦ. Стоит отметить, что при использовании пошагового метода , программа повторно обраб отала модель №1, установив истинность полученны х ранее значений.

Таблица 7 – Сводка для моделей № 2 и 3

Модель	R	R2	Скорректированный R2	S e
2	0,645	0,417	0,415	4,084
3	0,953	0,908	0,907	1,625

Согласно данным таблицы 7, коэффициент множественной детерминации (R2) для модели №2 составил 0,417 или 41,7%, для модели №3 – 0,908 или 90,8%. В первом случае мы можем сделать вывод, что долю изменчивости ОПЦ независимая переменная – МП объясняет лишь на 41% случаев. Тогда как совокупность индексов МП и Ф демонстрировали почти 91%.

Таблица 8 – МНК-оценка параметров квадратичных моделей пошагового метода

Модель		НК		СК	т	p
		B	SEM
2	(Константа)	55,880	5,329		10,486	0,0005
	МП	0,637	0,044	0,645	14,514	0,0005
3	(Константа)	-67,860	3,774		-17,982	0,0005
	МП	1,032	0,020	1,046	51,344	0,0005
	Ф	0,683	0,017	0,807	39,630	0,0005

По таблицы 8 видно, что все индексы, введенные в модели №2 и 3, имеют значительный вклад при формировании константы – на уровне 0,0005. Осно- вываясь на значениях нестандартизированных коэффициентов и переменных отклика, построим уравнения регрессий.

Уравнение регрессии для модели №2 будет иметь следующий вид:

ОПЦ=55,880+0,637*(МП);

ОПЦ=55,880+0,637*(130)= 138,69 .

Уравнение регрессии для модели №3 будет иметь следующий вид:

ОПЦ=-67,860+1,032*(МП)+0,683(Ф);

ОПЦ= ОПЦ=-67,860+1,032*(130)+0,683(110)= 141,43 .

Полученные результаты демонстрируют, что индекс общей племенной ценности также соответствует предсказанным значениям, включенным в диапазон минимального и максимального показателей – 123,51149,73. При этом совокупность независимых переменных оказывает на увеличение показателя большее влияние.

Выводы. Таким образом, результаты проведения регрессионного анализа вне зависимости от применяемого метода наглядно демонстрируют высокую степень взаимосвязи между переменными. Средние значения общей племенной ценности при построении уравнения регрессии составили для 1, 2 и 3 моделей 141,6; 138,7; 141,4 соответственно. Согласно разработанной спецификации по оценке племенного потенциала быков-производителей, показатель ОПЦ (GZW), принимающий значения близкие к 150, свидетельствует о наибольшей ценности животных.