Оценка погрешностей определения параметров движения по информации инерциального измерительного блока

оценивания параметров движения с помощью ФК на основе различных вариантов математических моделей датчиков и фильтров.

Методика и последовательность проведения исследования. Рассматривалась динамическая система, построенная на основе передаточная функций чувствительного элемента (ЧЭ) датчика, и математических моделей, описывающих сигналы и шумы ЧЭ. Реализация математических моделей ФНЧ и ФК осуществлялась на основе стандартных библиотек программы MatLAB Simulink. Исследовалась эффективность работы ФК и ФНЧ при оценивании полезного сигнала с возмущениями в виде белого или цветного шума, а также натурных сигналов микромеханических гироскопов (ММГ) и акселерометров (ММА). Блок-схема программы моделирования в Simulink MatLAB приведена на рис. 1.

Оценки сигналов н М I simm

Сигнал ЧЭ

Генератор белого шума

• •    03 ⁴ * ¹

• •    Фильтр Калмана для модели датчика без ФНЧ

• •    03] н « । »                                з

Фильтр Калмана для модели датчика 2-го порядка

_ , Kalman _ _ ,        .----—----.

Filter ^z-”* н ^11,3 I

Генератор синусоиды с частотой 30Гц

Фильтр Калмана

для ФФ 1-го лоэядка

Рис. 1. Структурная схема математического моделирования

При математическом моделировании рассматривалась динамическая система [4]

x[n +1] = A • x[x] + B • u[n] + G • w[n], yv [n ] = C • x[n ] + D • u [n] + H • w[n] + v[n ] (1)

с известными входами динамической системы u и возмущениями по входам w и измерениям ν , которые являются «белым» шумом со следующими характеристиками:

ЛГ {w} = М {v} = О, М щГО ■ w(r)^r ; = Q ■ 6\t — г)

M {и V) ’ ^v(^r)^T } = ^" sk) — t), M {v(O ■ u^r)^r} = TV ■ оУ — г)

где A - матрица состояния; В - матрица управления; G - матрица ошибок; С - матрица измерений; D - матрица прямой связи; Н - матрица шумов наблюдения; R, О, N- матрицы ковариаций.

В этом случае фильтр Калмана описывается уравнениями:

х[» +1] = А ■ Ар?] + В ■ «[»] + £ ■ (у_у — С ■ х[и] -D л[л]).

- Г-Д»] |я«]

С-(/-АС)1    Г(/-С рув СЕ

■х[п] + ■          ■

I-F-C        -FD Е

?/[??] _34И_

где матрица коэффициентов Ьи новая матрица коэффициентов обратных связей F определяется на основе решения матричного алгебраического уравнения Риккати. Обновленная матрица коэффициен тов обратных связей F применяется для того, чтобы уточнить предсказание х[п] на основе измерения УИ- х[и +1] = х[и] + F ■ (>’„[»]- С ■ х[?Л — D ■ ?/[//])

где х[и + 1] - оценка сигнала, I - единичная матрица, F- матрица коэффициентов обратной связи.

Математическая модель формирующего фильтра. При построении математической модели ФК применяется динамическая система, описываемая дифференциальным уравнением преобразования входного белого шума цифровым формирующим фильтром. Рассмотрим дифференциальное уравнение ФФ первого порядка [1]:

х(0+ А ■ ^(О = ^^deP ■ ^<0 ₍₅₎

на вход которого поступает белый шум w(0 единичной интенсивности И с дисперсией ^, на выходе образуется экспоненциально - коррелированный случайный процесс.

Дифференциальное уравнение математической модели ФФ запишем в виде:

0,003183 ■ х +1 • х = 1,414 • ivf t)        ^

Преобразовав уравнение (6) к дискретному виду получим выражение:

х1>л+1 = х1л.(1-314Д6.Т)+44^^

где Т - период квантования, равный 2е-О5с, величина которого задавалась в соответствии с условиями числовой устойчивости этого и последующих рекуррентных уравнений ЧЭ.

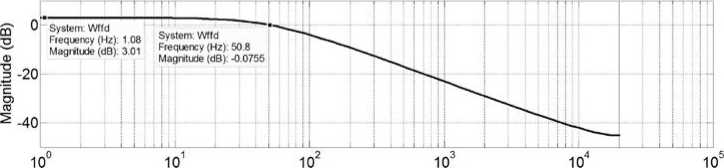
График АЧХ формирующего фильтра (7) приведен на рис. 2. Из графика АЧХ ФФ видно, что полоса пропускания составляет 50,8 Гц.

Freauencv fhM

Рис. 2. График АЧХ ФФ

Упрощенные математические модели

ММА. Для учёта в уравнениях фильтра Калмана параметров акселерометра воспользуемся математической моделью ММА ADXL 203 [5] структурная схема которой приведена на рис. 3.

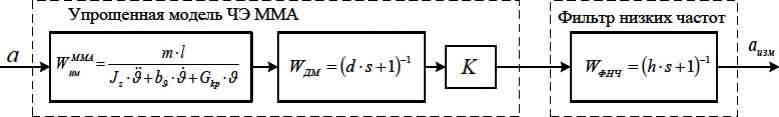
ттл-МШ пл ттл

Рис. 3. Упрощенная математическая модель ММА маятникового типа ' им , Дм , фнч - передаточные функции ЧЭ ММА, демодулирующего фильтра и ФНЧ выходного каскада, К - коэффициент усиления

Запишем дифференциальное уравнение усеченной математической модели ММА:

8,374 e - 10 • x + 5,788 e - 06 • x + 1 - x = 0,011 - U

В уравнении (8) не учтены члены с производными выше второго порядка на основании проверки устойчивости и частотных характеристик полной и усеченной моделей. Аналогичное усечение проводилось и с другими моделями для снижения порядка ФК.

Преобразовав уравнение (8) к дискретному виду получим выражения:

_< ^x 1, n + 1 = x 1 n ⁺ T • ^x 2 n ,

\ x _{2 n} = - 1.1942e + 09 • T • x 1 _n + (1-1.0494e + 10 • T ) • x _{2 n}

+ T • 1.3136e + 07 • U 1 _n

Матрицы пространства состояний:

фнч мма

A^чэ мма

T

T • 1.313e + 07

График АЧХ ММА без ФНЧ приведен на рис. 4.

- 1.1942e + 09 • T (1-1.0494e + 10 • T )

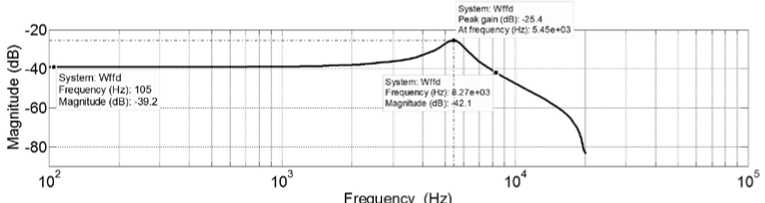
Рис. 4. График АЧХ ЧЭ ММА

Дифференциальное уравнение усеченной математической модели ММА с учётом фильтра низких частот выходного каскада запишем в виде:

9,165 e - 08 • x + 0,003213 • 5c + 1 x = 0,9983 • U

Преобразовав уравнение (11) к дискретному виду получим выражения:

f x1, n+1 = x1 n + T • x 2 n , tx 2n =-1.0911e + 07 • T • x1 n + (1-3.5057e + 04 • T) • x 2n + T •1.0893e + 07 • U1 n,

мма

Матрицы пространства состояний:

B

фнч мма

- 1.0911e + 07 • T

T

(1-3.5057e + 04 • T )

T • 1.0893e + 07

График АЧХ ММА с ФНЧ приведен на рис. 5.

Рис. 5. График АЧХММА с ФНЧ

Из рис.4, 5 видно, что полоса пропускания ЧЭ составляет 8,27e+03 Гц, с учетом ФНЧ она сужается до 50,1 Гц.

Упрощенная математическая модель ММГ. В качестве датчика угловой скорости рассматривался ММГ типа CRG20, построенный по RR-схеме вибрационного гироскопа. Упрошенную математическую модель ММГ представим в виде [6, 7]:

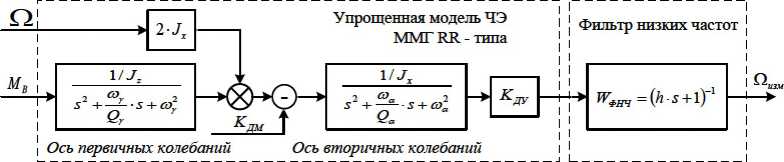
Рис. 6. Упрощенная математическая модель ММГ RR-типа:

где - ^юг , ®<х - угловые частоты колебаний ИМ, Qy, Qa- добротности, ^, J_z- моменты инерции ротора, Q - входная угловая скорость, М _в - момент привода инерционной массы, ^ду - коэффициент датчика угла, К₃м - коэффициент датчика момента, ^_и™ - измеренное значение угловой скорости

Дифференциальное уравнение упрощенной математической модели ЧЭ ММГ [8]:

х + 0,6406е - 06•х + 1,026е + 07 ■ х = 1,905е + 06 ■ U

Преобразовав уравнение (14) к дискретному виду получим выражения:

■\n+i = ты+г'^2^

х_2л = 1.02 бе + 07 ■ Т ■ х_1л + (1 - 0,6406е - 06 Т^ х_2л + Г 1,905е + 06 -Ц_и

Матрицы пространства состояний:

Г-1,905е + 06

-1,026е + 07-Г (1 - 0,6406е — 06 ■ Г)

График АЧХ ММГ без ФНЧ приведен на рис. 7.

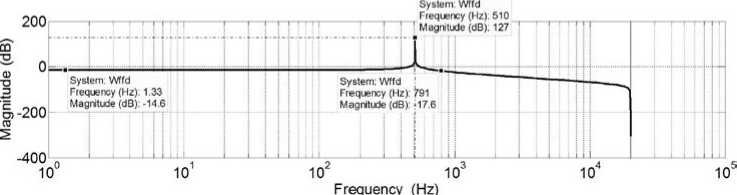
Рис. 7. График АЧХ ММГ без ФНЧ

Дифференциальное уравнение усеченной 1,002 х+ 26120■ х +1,026е + 07 = 1,905е + 06-67 математической модели ЧЭ ММГ с учётом филь-                                    (17)

тра низких частот выходного каскада:

Преобразовав уравнение (17) к дискретному виду получим выражения:

Х„+1 =Х1П+Г-Ж2П>

|х,„ =-1.0240е + 07-Г-х1п + (1 - 2.6067е + 04-Г)-х2„ + Г-1,9012е + 06

277                                                171 X                                        2                                                      171                              / 1 у

<Ф™ —

ЛШ2

Матрицы пространства состояний:

1                             Т '

-1.0240е + 07 ■ Т (1 - 2.6067е + 04 ■ Т)

уф™

о

Г-1.90126 + 06

График АЧХ ММГ с ФНЧ приведен на рис. 8.

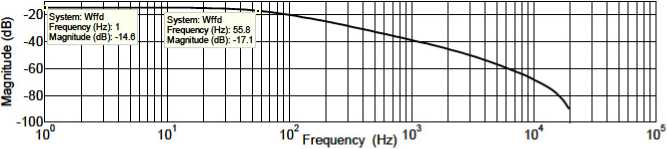
Рис. 8. График АЧХ ММГ с ФНЧ

Из графиков 7, 8 видно, что полоса пропускания математической модели ММГ без ФНЧ составляет 791 Гц, с ФНЧ - 55,8 Гц.

Результаты анализа погрешностей при стационарных и нестационарных возмущениях. Для анализа погрешностей использовались натурные записи сигналов ММГ марки CRG20 (ф. Sili-conSensing) и ММА марки ADXL203 (ф. AnalogDevices) на неподвижном основании с возможностью наложения полезной составляющей различного вида. Результаты сравнивались с оценками этих сигналов при наложении белого шума в качестве порождающего и измерительного шумов. Получено, что применение стационарного линейного фильтра низких частот с полосой пропускания 50 Гц на осно- ве ФНЧ первого порядка позволяет снизить шум датчика до 4.0244e-04 ед. (СКО) при входном шуме 0.0010 ед. (СКО). В результате анализа погрешностей ФК на основе математических моделей ЧЭ датчиков (ММГ и ММА) получено, что снижение шумов практически не происходит. При работе ФК на основе математической модели ЧЭ ММА (по формуле 12) шум снижен до 9.9677e-04 м/с2 (СКО), а при ФК на основе математической модели ЧЭ ММГ (по формуле 18) до 9.9671e-04 град/с (СКО).

Для определения влияния ФК на основе ЧЭ ММА (ЧЭ ММГ) построен амплитудный спектр ошибки оценивания (рис. 9), вычисленный как разность входного белого шума и выходного сигнала после ФК на основе ЧЭ ММА.

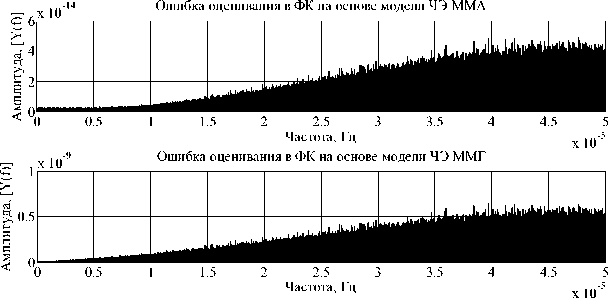
Рис. 9. График амплитудного спектра ошибки оценивания при обработке в ФК на основе модели ЧЭ ММА и ЧЭ ММГ, [ у ( f ) ] = [ м / с ² Гц ]

Из графика видно, что амплитудные спектры сигналов после обработки в ФК с учётом математических моделей ЧЭ ММА и ММГ соответствует идеальным АЧХ, приведенным на рис. 3 и 6. В результате анализа погрешностей ФК на основе математической модели ЧЭ ММА (ЧЭ ММГ) с учётом фильтра низких частот получено (уравнения 14 и 20), что при наличии белого шума с СКО 0.0010 м/с2 (град/с) ошибка снижена до 6.5225e-04 м/с2 (СКО) и 6.4969e-04 град/с (СКО) для ММА и ММГ соответственно.

0.04

ФК для модели ЧЭ ММА с ФНЧ

0.02

S ч с

S

0.04

0.02

S ч с

S

100    150    200    250    300    350    400    450    500

Частота, Гц

ФК для модели ЧЭ ММГ с ФНЧ

100    150    200    250    300    350    400    450    500

Частота, Гц

Рис. 10. График амплитудного спектра ошибки оценивания при обработке в ФК на основе модели ММА с ФНЧ сигнала белого шума, [ у ( f ) ] = [ м / с ² Гц ]

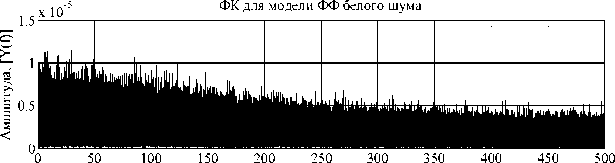
Из графиков амплитудных спектров (рис. 10) видно, что полоса пропускания ФК для модели ФФ, модели ММА и модели ММГ практически соответствует идеальной АЧХ (рис.4 и 7). На графике видно, что в полосе пропускания сигналы амплитудного спектра ФК идентичны. После частоты 50 Гц наблюдается спад АЧХ. В результате анализа погрешностей ФК первого порядка на основе математической модели ФФ (уравнение 7) для белого шума получено, что при оценивании сигнала белого шума с СКО 0.0010 м/с2 (град/с) ошибка снижена до 6.6766e-04 м/с2. На графике амплитудного спектра (рис. 11) видно, что полоса пропускания ФК для модели формирующего фильтра составляет 50 Гц. В табл. 1 сведены результаты вычислений статистических характеристик моделирования ФК на основе различных вариантов математических моделей.

Частота, Гц

Рис. 11. График амплитудного спектра ошибки оценивания при обработке в ФК на основе ФФ, [ У ( f ) ] = [ м / с ² Гц ]

Таблица 1. Результаты вычислений статистических характеристик моделирования

Статистическая характеристика сигнала	Статистические характеристики сигнала
	СКО, м/с2	Дисперсия, м2/с4	Матем. ожидание, м/с2
Параметры входного белого шума	0.0010	1.0009e-06	2.1592e-06
Фильтр низких частот	4.0244e-04	1.6196e-07	-3.7106e-0
ФК для математической модели ММА без ФНЧ (2 порядка)	9.9677e-04	9.9355e-07	1.6409e-05
ФК для математической модели ММГ без ФНЧ (2 порядка)	9.9671e-04	9.9343e-07	1.6409e-05
ФК для математической модели ММА с ФНЧ (2 порядка)	6.5225e-04	4.2542e-07	-3.6302e-06
ФК для математической модели ММГ с ФНЧ (2 порядка)	6.4969e-04	4.2209e-07	-3.6306e-06
ФК для ФФ (1 порядка)	6.6766e-04	4.4577e-07	-3.6283e-0

Из таблицы 1 видно, что при подавлении белого шума наибольшую эффективность показал линейный ФНЧ. Применение ФК на основе математической модели ЧЭ без учёта ФНЧ не приводит к снижению шумов. Оценим эффективность применения ФК при обработке натурного сигнала ММА ADXL203 и ММГ CRG20 в статическом режиме работы на неподвижном основании. Результаты работы при оценке в ФК сигналов ММА приведены в табл. 2.

Результаты моделирования при оценке в ФК сигналов ММГ приведены в табл. 3. Из табл. 2, 3 следует, что применение ФК для ФФ и ФК для математической модели ММА (ММГ) с ФНЧ позволяют практически с одинаковой эффективностью снизить ошибку оценивания полезного сигнала. На рис. 12 показаны амплитудные спектры сигналов ММА и оценок в ФК. На рис. 13 показаны амплитудные спектры сигналов ММГ и оценок в ФК.

Таблица 2. Результаты работы при оценке в ФК сигналов ММА

Статистическая характеристика сигнала	Статистические характеристики сигнала
	СКО, м/с2	Дисперсия, м2/с4	Матем. ожидание, м/с2
Параметры входного шума ММА	0.0063	3.9233e-05	1.2510e-04
Фильтр низких частот	0.0055	3.0774e-05	-3.9078e-05
ФК для математической модели ММА без ФНЧ	0.0063	3.9230e-05	1.2510e-04
ФК для математической модели ММА с ФНЧ	0.0050	2.5246e-05	-3.8926e-05
ФК для ФФ (1 порядка)	0.0047	2.2232e-05	1.2441e-04

Таблица 3. Результаты моделирования при оценке в ФК сигналов ММГ

Статистическая характеристика сигнала	Статистические характеристики сигнала
	СКО, м/с2	Дисперсия, м2/с4	Матем. ожидание, м/с2
Параметры входного шума ММГ	0.5127	0.2629	-0.0654
Фильтр низких частот	0.4327	0.1873	-0.0652
ФК для математической модели ММГ без ФНЧ	0.5127	0.2629	-0.0654
ФК для математической модели ММГ с ФНЧ	0.3451	0.1191	-0.0651
ФК для ФФ (1 порядка)	0.3535	0.1250	-0.0652

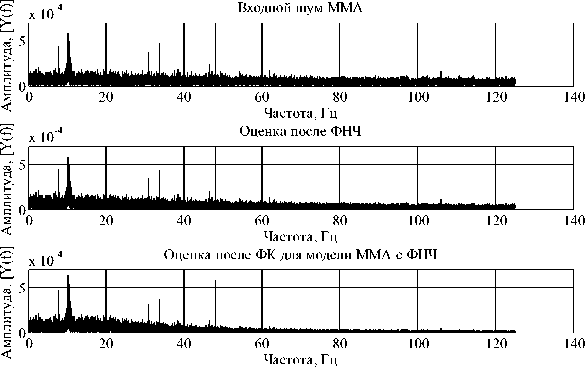
Рис. 12. График амплитудного спектра ошибки оценивания при обработке в ФК сигнала ММА, [ у ( f ) ] = [ м / с ² Гц ]

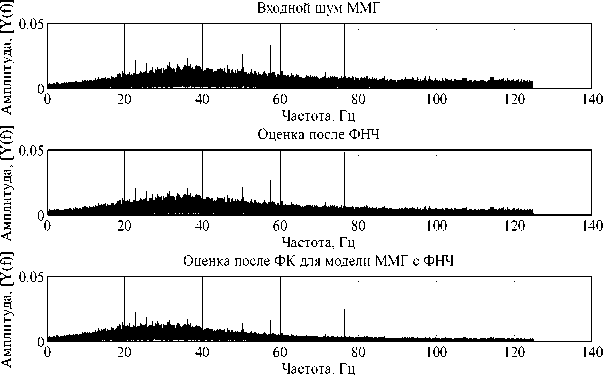
Рис.13. График амплитудного спектра ошибки оценивания при обработке в ФК сигнала ММА, [ у ( f ) ] = [ м / с ² Гц ]

При обработке в ФК на основе математической модели ММА и ММГ с учетом ФНЧ на амплитудном спектре наблюдается снижение помехи после частоты 50 Гц. Оценим эффективность работы ФК при обработке нестационарного сигнала в виде синусоиды частотой 30 Гц с наложенным белым шумом. Применим интегральную оценку погрешностей определения полезной составляющей сигнала за время 60 с. Результаты моделирования нестационарного приведены в табл. 4. Из табл. 4 следует, что при обработке нестационарного сигнала в ФК для математических моделей ММГ и ММА с ФНЧ интегральные значения ошибки оценивания полезного сигнала (синусоиды) на порядок меньше, чем другие варианты алгоритмов.

Таблица 4. Результаты нестационарного моделирования

Статистическая характеристика сигнала	СКО шума, ед/с	Интегральная оценка ошибки ед/с
Параметры входного шума	1.0083e-03	1.8819e-06
Фильтр низких частот	4.0244e-04	1.3246e-06
ФК для математической модели ММГ без ФНЧ (2 порядка)	1.0083e-03	1.8819e-06
ФК для математической модели ММГ без ФНЧ (2 порядка)	9.4502e-04	1.6680e-06
ФК для математической модели ММГ с ФНЧ (2 порядка)	6.4592e-04	1.2677e-07
ФК для математической модели ММА с ФНЧ (2 порядка)	6.4293e-04	1.2052e-07
ФК для ФФ (1 порядка)	6.6520e-04	1.6105e-06

Выводы:                                   3.

• 1.    При построении алгоритмов оценивания полезных составляющих сигналов на фоне шумов ММА ADXL203 и ММГ CRG20 нецелесообразно учитывать математические модели датчиков выше второго порядка.

• 2.    При обработке сигналов датчиков на неподвижном основании наибольшую эффективность, в   4.

• 3.    При моделировании обработки сигналов дат-   ₅

смысле снижения СКО погрешности, показал ФК на основе формирующего фильтра первого порядка и штатный ФНЧ ММА. При обработке натурных сигналов датчиков этот эффект усилился.

чиков на подвижном основании интегральные зна-    ^.

чения ошибок оценивания полезной составляющей сигнала в ФК на основе математической модели датчиков с учётом ФНЧ за 60 с. на порядок меньше, чем дают другие рассмотренные варианты алго-    6.

ритмов.