Оценка погрешности численного метода решения одной обратной задачи

В различных приложениях, например, в теории динамических измерений [1], возникают проблемы, приводящие к краевым задачам для обыкновенных дифференциальных уравнений с неклассическими краевыми условиями – многоточечные краевые задачи, задачи с распределенными данными и т.п.

Многие подобные задачи могут быть сформулированы как линейные краевые задачи:

Г L [ x ]= x ( n ) + P n- 1 x ( n 1) ++ p 1 x + p 0 x = f ( t ) ,

I Uj(x)     aj, j 1,2, *.., n, где Pi (t) , f (t) - непрерывные на [a,b] функции, aj - числа, Uj (x) - линейные, линейнонезависимые функционалы.1

Краевая задача (1) — это прямая задача нахождения x ( t ) при заданной f ( t ) . Задачу нахождения правой части f ( t ) по экспериментально измеренной функции e( t ) будем называть обратной задачей .

1.    Метод обращения

Одним из наиболее эффективных методов решения обратной задачи является метод обращения дифференциального оператора (1) с помощью функции Грина, использующий хорошо известное соотношение для решения полуоднородной краевой задачи:

b j G(t,T)f (т)dT = x(t), a

где G ( t,T ) - функция Грина этой задачи.

1 Без ограничения общности можно считать, что aj = 0.

В.И. Заляпин, Ю.С. Попенко, Е.В. Харитонова

Содержательной частью описываемого метода является построение функции Грина G ( t, т ) , осуществляемое в два этапа - сперва строится функция Грина G ( t,т ) вспомогательной задачи

Г x ⁽ n ) = f ( t) ,

I Uj(x) = 0, j = 1, 2 ,...,n, которая может быть найдена непосредственно по определению с использованием фундаментальной системы решений соответствующего однородного уравнения.. На втором этапе численно отыскивается функция Грина основной задачи G(t, т), оказывающаяся решением интегрального уравнения Фредгольма II-го рода:

b

G ( t,s )

-

G ( t,s ) = J

G ( t, т ) V ( т, s ) dт.

a

Детали и необходимые подробности можно найти в [2, 3].

На основании этих соображений был построен алгоритм решения обратной задачи теории, и написана компьютерная программа с использованием пакета Mathematica 8.0. ²

Предложенный подход поддается распараллеливанию, которое было реализовано [4] с использованием языка Си++ и стандарта MPI-2 (Message Passing Interface). Программа для высокопроизводительного вычислительного кластера « СКИФ Аврора » суперкомпьютерного центра ЮУрГУ (8832 вычислительных ядра, 117,64 триллиона операций в секунду) находится в стадии разработки. Подробности в [4].

2.    Регуляризация

Важным вопросом, возникающим в контекстсте описанной выше процедуры, является вопрос о точности получаемого решения. Численная реализация метода предполагает последовательное решение двух интегральных уравнений – уравнения (4) для нахождения функции Грина G ( t,т ) и уравнения (2) для нахождения функции f ( t ) . И если первая из задач особых проблем в плане точности получаемого численного решения перед исследователем не ставит – уравнение (4) является уравнением Фредгольма II рода, то вторая относится к классу задач, решения которых неустойчивы к малым изменениям исходных данных. Поскольку правая часть рассматриваемого уравнения – экспериментально определяемая функция e( t ) , а ядро - результат применения численных процедур решения уравнения (4), то для нахождения решений уравнения (2) необходимо так построить процедуру решения, чтобы погрешности в определении ядра и правой части не сильно портили ее решение – рассматриваемую задачу необходимо регуляризовать.

Мы использовали метод регуляризации А.Н. Тихонова [5], сводящий задачу решения уравнения (2) к задаче минимизации функционала

M ^а = kAf - x| |² + а • Q ² ,                               (5)

где - Q ² стабилизатор, взятый в виде

b

Q ² = j p ( t ) f ² ( t )

dt,

P ( t ) >  0 ,

a

α – параметр регуляризации, который определяется из условия минимума невязки и зависит от точности задания правой части уравнения (2).

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

Напомним, что псевдорешением операторного уравнения Af = x называется решение f, минимизирующее невязку x = arg inf || Af — x|| .

Уравнение может иметь несколько псевдорешений. Обозначим через Q совокупность всех его псевдорешений, и пусть ψ некоторый элемент из Q . Нормальным относительно ψ решением или ф - нормальным решением операторного уравнения называется псевдорешение f 0 с минимальной нормой kf - ψk , то есть такое, что

Il f 0 ^{— ф|} = f ^f Il f ^{— ф|} •

Если ф = 0 , то f 0 называется просто нормальным решением. Рассмотрим операторное уравнение

Af = x, f _e F, x _e X,

X и F – гильбертовы пространства, A – линейный вполне непрерывный оператор из F в X. Если вместо точных x и A известны их приближения x и A , такие, что

то фактически решается уравнение

Af = x, f € F, x € X.

Известно [5], что задача нахождения элемента f _α , на котором функционал (5) достигает минимального значения, имеет единственное решение. Это решение является нормальным решением, то есть при точных A и x из всех точных решений операторного уравнения в методе Тихонова автоматически выбирается нормальное решение. Если же 5 = 0 и/или е = 0 , то метод дает решение f _a , близкое к нормальному. Известные на сегодня оценки точности получены сравнением численного решения f _a и нормального решения f 0

A a f = Uf a — f 0 |.

3.    Оценивание точности по Винокурову В.А.

Наиболее удачными (с теоретической точки зрения) на этом пути нам представляются оценки, полученные В.А. Винокуровым [6].

Подробнее: пусть G = A * A, а G + - псевдообратный оператор. Тогда

I A Ы<;£= +

2 J а

α

(^{а +} | Ж )

|f 0 | ,

где A = 5 + е |f | _F .

В некоторых ситуациях оказывается полезной также оценка относительной ошибки ре-

шения. Она имеет вид:	I A f a ll _                                           m If I 5 E( а ) '                                         (7)
где	II A ° 17/ \ H H ( 5 otn + e otn )        pa E( а )= 2       VS     1 pa +1 ’

В.И. Заляпин, Ю.С. Попенко, Е.В. Харитонова причем

II -II II ~ II2                     6                         £ p = IIGII = II1 II ,       = x,  £otn = PF’

При A ^ 0 I I A f a F ^ 0 , если только выполнено a (A) = O (A ² ) .

Одновременно, полученные В.А. Винокуровым оценки дают возможность получить оп- тимальное значение параметра регуляризации αopt из соотношения a=

P I I ( 6 otn + £ otn ) 1 3

4 p

(1 + pa ) ³ .

Для нахождения решения уравнения (8) можно воспользоваться итерационными процедурами либо приближенным соотношением

α opt

P I I ( 6 otn + £ otn ) ^{1 3}

4 p

¹⁺ 3 p(

p I I ^{( 6} otn ^{+ £} otn ) ³

4 p

которое справедливо, если только

p

p I I^{( 6} otn ^{+ £} otn )

4 p

<< 1 .

Эффективные с теоретической точки зрения соотношения (6) – (9) мало пригодны для практической оценки точности получаемых решений.

4.    Эмпирическая оценка погрешности

• 4.1.    Дискретизация

Зададим на промежутке [ a ; b ] сетку a < t о < t 1 < ... < t n = d . Положим f ( t ) ~ u n ( t ) ,

где

n

U n ( t ) = ^u n X i ( t ) , i =0

X i ( t ) — базис Лагранжа конечно-элементных аппроксимаций. В дальнейшем ограничимся использованием подпространств кусочно-линейных функций, где X i ( t ) задаются соотноше-

ниями

0 ,    t < t i- 1 U t > t i +i ,

X i ( t ) =

t — t i- 1

t i ^- t i +1 t ^— t i +1

t i - t i +1

ti-1 < t < ti, ti < t < ti+1.

M ^α

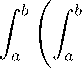
G ( t,T ) XX u n X i ( т ) dT i =1

-

\ ²            „ ь / n            \ ²

x ( t ) I dt + a p l У^ u n X i ( т ) I

)         J a   \i =1         /

dτ.

Обозначив через J i ( t ) интеграл J b G ( t, т ) X i ( т ) dT , получим:

M ^α

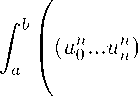
J ₀

.

.

.

J n J 0

J 0 J n

.

.

.

J _n

n

— 2£ u n J i ( t )

i =1

^  ^ 2

x + x

dt +

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

+ a ( u П ... u n )

J b ( P^X 2 ) dr   ... Jb ⁽ pX 0 A n ) d^T

•                                            .•

... .

J b ⁽ P^X n ^X 0 ) ^dт . ..   Jb ( P^X n ) d^T ,

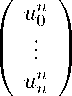
= X Mijunun-2 XX Wu+|5II2. i,j=0

Необходимое условие минимума функционала M ^α запишется в виде

∂M ^{α n}

—---= V^ Mis^n — 2 W_s = 0 ,  s = 0 , 1 , 2 , ...n.

∂un               is i          s ,            ,  , , s     i=0

В итоге получаем систему n + 1 линейных уравнений

n

X Misun = 2Ws, s = 0"П, i=0

которая и подлежит решению.

Параметр регуляризации α определялся итерационно по принципу невязки [5].

Построенные таким образом конечномерные приближения u “ ( t ) сходятся (например, [7]) к точному решению задачи при выполнении некоторых дополнительных условий. Контроль вычислений по схеме, изложенной выше, осуществлялся параллельным решением задачи конечномерной минимизации

• 4.2.    Оценивание точности решения уравнения (4)

Ядро уравнения (2) определялось в результате решения интегрального уравнения (4), являющегося при каждом фиксированном значении переменной a ≤ t ≤ b уравнением Фредгольма второго рода относительно функции G ( t, т ) = Ф _t ( т ) :

^Ф t ⁽ s )

-

b

G ( t,s ) = /

Ф t ( т ) V ( т, s ) dT,

а

ядро которого V(s,т) определяется функцией Грина G(t,т) вспомогательной задачи. Положив при каждом фиксированном значении a ≤ t ≤ b a = то <т1 < ... < тп = b,     Ф t = Ф( t,Ti),     Gt = G (t,Ti),

получим nn ф t (т) = £ф tXi (т) ,G( t,т) = 52 GtXi (т). i=0                      i=0 Обозначая Vi = / Xi (s) V (s,Tj) ds, i,j = 1, 2 ,...,n, a и подставляя в (4), приходим к дискретному аналогу рассматриваемого уравнения

n

52 Ф t ( X i ( T j ) — Vi )= ( G t , j = 0 , 1 ,...,n, i =0

В.И. Заляпин, Ю.С. Попенко, Е.В. Харитонова представляющему собой систему линейных алгебраических уравнений относительно неиз- вестных Фt. В матричной форме

( I — V )Ф t = G t

где

/ Ф 0 \

Ф 1

...

\ Ф n /

/ G0 \            / 1 — V?

^V 0 ⁿ

^V 1 ⁿ

...

1 — V /

G ¹    , I — V =      V 1 ^{0    1} - V ¹

...                                           ......

\ G n /          \  Vn

Поскольку задача решения уравнения Фредгольма второго рода корректна, и исходное интегральное уравнение (4) однозначно разрешимо, то для каждого значения N соответствующая дискретная задача однозначно разрешима. При этом конечномерные решения сходятся к точному решению уравнения.

Пусть Gn ( t,T ) - решение уравнения (4), полученное при n = N . Из вышеизложенного следует, что точность нахождения ядра уравнения (2) из уравнения (4) может быть оценена разностью двух соседних приближений для достаточно больших значений N :

AG = ||GN+i — Gn II, что дает возможность оценить величину ε – точность задания оператора A, поскольку:

A A = |A — A1 | = A G <  e.

• 4.3.    Оценивание точности решения уравнения (2)

Основные соображения, положенные в основу метода оценки точности решения уравнения (2), состоят в следующем: параллельно с задачей решения уравнения (2) относительно неизвестной функции f решается по тому же алгоритму модельное уравнение

b j G(t,T) f (T)dT = xmod(t).

a

Пусть – f _mod – известное точное решение уравнения (10) для точно известной правой части x _mod , f _mod – решение, полученное регуляризацией. Точность метода оценивается величиной A M f = If mod — f mod I .

В случае неточного задания ядра и/или правой части уравнения (2) поступаем следующим образом: возмутим точное решение уравнения (10), положив f pert ( t ) = f _mod + f ( t ) , и построим возмущенную правую часть для уравнения (10), положив x mod = x mod + п ( t ) , где П ( t ) дается соотношением

b

п ⁽ t ) = 1^{G ( t,T} ) ^ ^{( T} ) d^T‘

a

Регуляризованное решение уравнения (10) с правой частью x mod обозначим через f pert и сравним его с f mod , положив A S f = I f mod — f pert l .

Модельная задача может быть построена многими способами. Например, если есть априорная информация о структуре и поведении отыскиваемого решения f ( t ) , то в качестве x _mod ( t ) следует взять функцию

b xmod (t) =

G ( t,T ) g ( т ) dT,

a

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ где g (t) — аналог (в каком-то смысле) функции f (t).

Если априорная информация отсутствует, то на грубой сетке ( n не очень велико) отыскивается регуляризованное решение уравнения (2) и в качестве аналога g ( t ) функции f берется сглаженное (например – сплайнами невысокого порядка) регуляризованное решение.

Описанная выше эмпирическая методика оценивания точности показала свою эффективность при решении различных прикладных задач.