Оценка потенциальной помехоустойчивости алгоритма распознавания вида модуляции узкополосных сигналов методом численного моделирования

DOI:

где A ( t ) и 0 ( t ) - медленные в сравнении с го ₀ 1 функции времени (амплитуда и фаза).

При приеме и демодуляции подобных сигналов необходима предварительная оценка типа модуляции, которая может быть произведена во временной области на основе интегрального критерия узкополосности, предложенного в работе [4]. В соответствии с этим критерием вид модуляции радиосигнала – амплитудная (АМ) или угловая (ФМ, ЧМ) оценивается по вкладу в левую часть неравенства

dA dt

+

. d ® A

dt

<< ® 0,1 4

для чего необходимо вычислить и сравнить соответствующие нормы. Если основной вклад в расширение спектра осуществляет норма производной огибающей

dA dt

>>

, d © A , dt

то сигнал (1) следует считать амплитудно-модулированным. Если же расширение спектра в основном обязано второй норме dA dt

<<

, d ©

A

dt

то мы имеем дело с угловой модуляцией сигнала. Конкретный ее вид (ЧМ или ФМ) можно установить только на основании априорной информации о типе модулятора на передающей стороне. Соответствующие нормы в соотношениях (3) и (4) должны быть вычислены во временной области по модели сигнала (1) на основе определений огибающей и фазы с использованием преобразований Гильберта [2].

Структура алгоритма приведена на рисунке 1 и содержит два квадратурных канала и блоки выполнения отдельных операций.

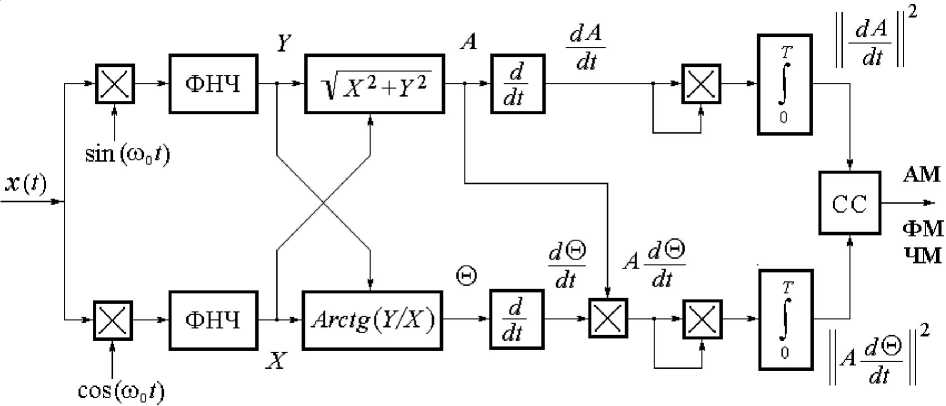
Рис. 1. Структура алгоритма распознавания вида модуляции по интегральному критерию

Перемножитель и фильтр низких частот (ФНЧ) представляют собой коррелятор разностной частоты [1], формирующие квадратурные компоненты X и Y для вычисления огибающей A ( t ) и фазы © ( t ) узкополосного сигнала. Схема сравнения (СС) осуществляет компарирование норм || dA/dt\ и || Ad®/dt\ |.

Методом численного моделирования в работе проведена оценка потенциальной помехоустойчивости алгоритма распознавания вида модуляции узкополосных радиосигналов путем расчета точности его работы на фоне аддитивных помех.

Для оценки помехоустойчивости использовались временные последовательности сигналов с тональной амплитудной x ₁ [ k ] и фазовой x ₂ [ k ] модуляцией вида

• x 1 [ k ] = A ₀[1 + m sin( Q k A t )]cos( m ₀ k A t );                             (5)

x 2 [ k ] = A ₀ cos[ o ₀ k A t + m sin( Q k A t )],                              (6)

где ю ₀ = 2 n f ₀ , f ₀ = 64,0 ; Q = 2 n F ; F = 1,0 ; A t = 0,001 , m = 0,5 , A ₀ = 1,0 , k = 1,...1024 .

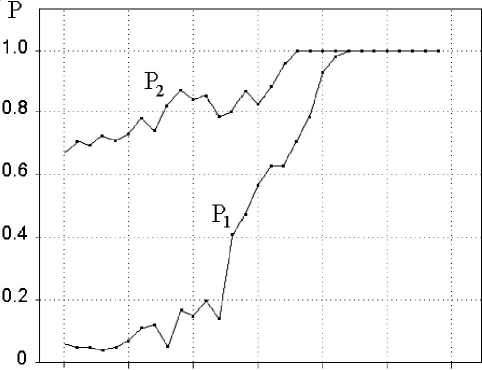
К каждой последовательности были добавлены отсчеты белого гауссова шума n(t) с распределением W(n) = N(0,оП). Затем во временной области вычислялись нормы || dA[dt^ и || Ad©/dt\\ по моделям сигналов (5) и (6) и производилось их сравнение. Методом статистического модели- рования определялась вероятность правильных решений при различном уровне аддитивного шума сn. Результаты моделирования получены усреднением по 200 значениям и представлены на рисунке 2, где приведены вероятности правильного распознавания P1 (для АМ-сигнала) и P2 (для ФМ-сигнала).

40   -30   -20   -10     0     10    20

А1/сг_п , dB

Рис. 2. Зависимость вероятностей правильного распознавания вида модуляции P ₁ (АМ) и P ₂ (ФМ) в сигналах (5) и (6) от отношения сигнал/шум

Следует отметить, что энергетические спектры последовательностей (10) и (11) достаточно близки, однако чувствительность идентификации к аддитивному шуму у них различна. Как следует из рисунка 2, предлагаемый алгоритм с большей вероятностью определяет сигналы с фазовой модуляцией, в то время как для правильной идентификации амплитудной модуляции (при P1 >  0,8) требуется отношение сигнала к шуму на 10 дБ выше, чем для фазовой.