Оценка потенциальной помехоустойчивости стробоскопического преобразователя периодических импульсных сигналов методом численного моделирования

DOI:

Стробоскопическое преобразование является эффективным методом обработки периодических сигналов, позволяющим сравнительно простыми техническими средствами согласовать частотный диапазон широкополосных импульсных сигналов с возможностями низкочастотной аппаратуры [10; 11]. Основным ограничением использования этого метода является требование к периодичности исследуемых сигналов на интервале наблюдения, однако в большинстве практических задач выполнение этого условия не представляет сложности. Временное квантование, присущее этому методу, хорошо сочетается с принципом цифровой фильтрации, что стимулирует использование стробоскопических методов в системах цифровой обработки сигналов наносекундной длительности [1; 6].

Преобразование временного масштаба широкополосных радиосигналов представляет значительный интерес в ряде задач локации и связи [4; 5]. В настоящее время потенциальные возможности стробоскопической трансформации наиболее полно реализуются в осциллографической технике. Так, например, произведение чувствительности на рабочую полосу частот у стробоскопических приборов на 2–3 порядка выше, чем у обычных аналоговых [3]. В реальных условиях радиоэлектронная аппаратура работает при действии различного вида помех, что сказывается на качестве ее работы. В этой связи представляет интерес оценка допустимого уровня внешних помех, не снижающих заданной погрешности работы стробоскопического преобразователя.

В радиотехнике под потенциальной помехоустойчивостью систем обычно понимается зависимость погрешности обработки сигнала от отношения сигнала к шуму на ее входе. В этой связи представляет интерес оценка допустимого уровня помех на входе стробоскопического преобразователя, не снижающих эффективность его работы. В предлагаемой работе производится расчет потенциальной помехоустойчивости стробоскопической обработки некоторых моделей периодических видео- и радиосигналов при действии на входе преобразователя нормального шума (аддитивная помеха) и при нарушении синхронизации входных сигналов и стробирующих импульсов (мультипликативная помеха).

1.    Линейная модель стробоскопического преобразователя

При теоретическом анализе в работе используется упрощенная линейная модель стробоскопического преобразователя (рис. 1), введенная А.И. Найденовым [10] и состоящая из мультипликативного элемента (См), осуществляющего перемножение входного и стробирующего сигналов и узкополосного фильтра (Ф), выделяющего одну из спектральных составляющих продуктов преобразования.

В качестве входных периодических импульсных сигналов использованы модели видеосигналов, представленных на рисунке 2 и описываемых соотношением (1) [7]:

N

x(t) = ^ X o (t - kT )

k=1

где T — период повторения; X 0 (t) — форма сигнала в одном периоде; X — число периодов. Параметры моделей: T = 64 ms; А _т = max(X ₀ (t)) = 10; X = 65.

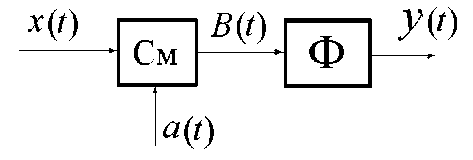
Рис. 1. Модель стробоскопического преобразователя

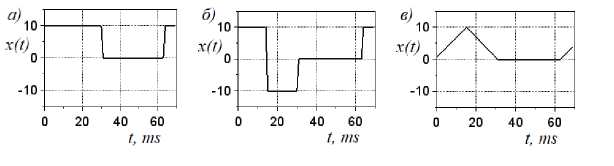
Рис. 2. Модельные видеосигналы: прямоугольной ( а ), биполярной ( б ) и треугольной ( в ) формы на входе стробоскопического преобразователя

Стробирующий сигнал a(t) имеет вид прямоугольного видеоимпульса A 0 (t) длительностью т _и = 3 ms с периодом следования Т 1 = 65 ms. Таким образом, шаг считывания составляет NT = Т 1 — Т = 1ms. Фильтрация выходного сигнала стробоскопического смесителя В(t) осуществлялась с использованием алгоритмов быстрого преобразования Фурье (БПФ):

y ^{( t )} = ^F 1W ^w) ^{F [ В} (i)] } ,

где k(j w) — частотная характеристика фильтра преобразователя (ФНЧ).

2.    Моделирование работы стробоскопического преобразователя видеосигналов на фоне аддитивных и мультипликативных помех

Для оценки потенциальной помехоустойчивости к последовательности исследуемых сигналов (1) добавлялся белый гауссов шум l(t) c распределением W (|) = N (0, а | ). Уровень шума (а | ) изменялся в пределах (0,05 — 1, 0)A _m . На рисунке 3 приведены результаты численного моделирования для видеосигналов с усреднением по 10 значениям. На них приведена относительная погрешность воспроизведения формы модельных сигналов (1) в зависимости от отношения сигнала к шуму A _m /^ i :

1 v ^{A V}II м ^ |ЛУ о |

1 ы

У му 2 = 1

N

£ (У [k] — Y ₀ [k]) ²

k=1

N

У ^ k

/г=1

где М =10 — количество усреднений.

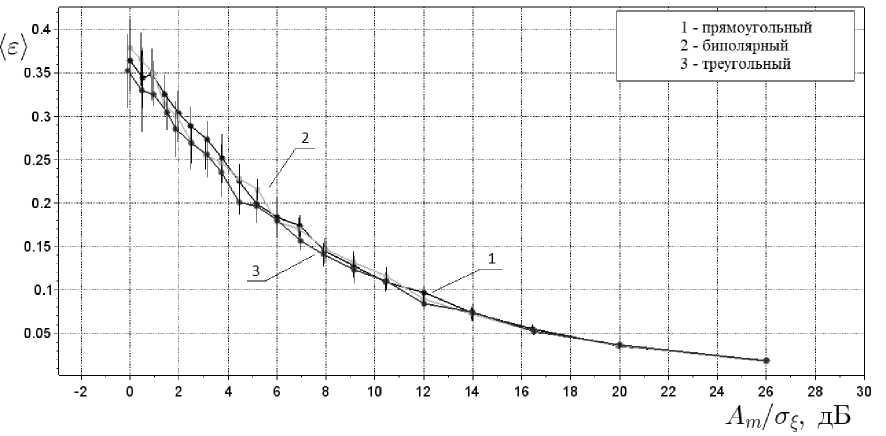
Рис. 3. Зависимость относительной ошибки воспроизведения от отношения сигнал/шум для прямоугольного (1), биполярного (2) и треугольного (3) видеосигналов

Как следует из графика, для обеспечения погрешности, например, для треугольного видеосигнала не более 18%, необходимо, чтобы уровень шума не превышал 6 дБ. Моделирование мультипликативной помехи для видео- и радиосигналов происходило путем вобуляции положения стробирующего сигнала по равновероятному закону распределения в пределах от 2 до 8 ms [9]. Численные значения параметров модели были выбраны в соответствии с рисунком 2. Среднеквадратичное отклонение строба определялось по формуле:

^ t =

V

Е [ р<М - <  р , >] ²

к=1

N -

где { P _t } — массив значений мультипликативного шума с равновероятным законом распределения; < P _t >  — среднее значение массива.

На рисунке 4 представлена зависимость относительной ошибки воспроизведения видеосигналов от временной нестабильности (a _t ) стробирующих импульсов. Так, например, для обеспечения погрешности не более 35%, необходимо обеспечить уровень временной нестабильности стробирующих импульсов для биполярного сигнала не более ~ 0, 5 ms.

3.    Моделирование обработки радиосигналов в схеме радиоимпульсного стробирования

Стробоскопическая обработка периодической последовательности радиосигналов предполагает когерентность исследуемых x(t) и стробирующих a(t) радиоимпульсов на интервале наблюдения t Е [0,NT] :

NN

x(t) = ^ X0(t — kT) cos(ш0t);     a(t) = ^ A0(t — kT1) cos(ш1t).

k=i

При стробоскопической обработке радиосигналов в модели преобразователя (рис. 1) фильтр нижних частот (ФНЧ) заменяется на полосовой фильтр, выделяющий спектральные компоненты на выходе смесителя в окрестности разностной частоты несущих Q = Шо — Ш 1 [8].

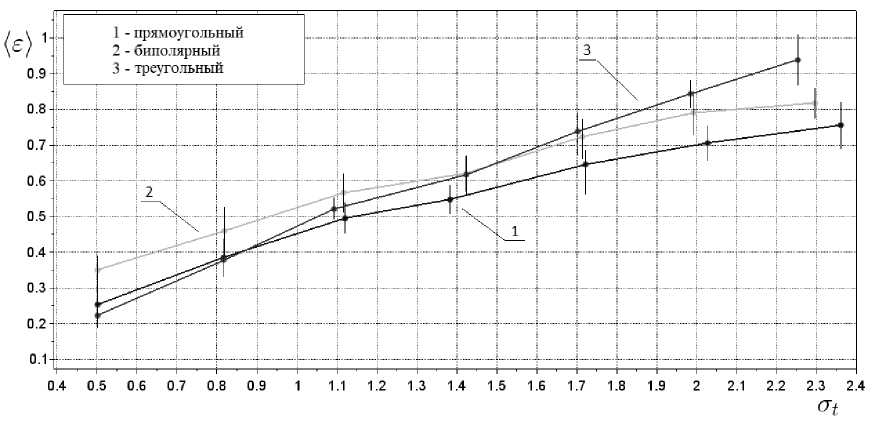
Рис. 4. Зависимость относительной ошибки воспроизведения видеосигналов от временной нестабильности ( о ) стробирующих импульсов для: прямоугольного (1), биполярного (2) и треугольного (3) сигналов

Для расчета помехоустойчивости использовались модели радиосигналов с прямоугольной и гауссовой огибающей, представленные на рисунке 5 и описываемые соотношениями (6) и (7) cоответственно:

a) X o (t) = Х _т при t £ [0, Т 1 ],   0 при t £ [0,T i ];

b) X o (t) = Х _т exp

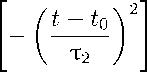
при t £ [0, 2t ₀ ],

0 при t / [0, 2t ₀ ].

Параметры моделей: Х _т = 10; t ₁ = 25 ms; т ₂ = 5 ms; t ₀ = 12, 5 ms; ш ₀ = = 2nf o ; f o = 1,0 kHz; Ш 1 = 2nf i ; f i = 0, 9 kHz.

Стробирующий радиоcигнал a(t) моделировался коротким радиоимпульсом прямо угольной формы с несущей частотой f1, длительностью 5 ms и периодом повторения

T1 = T + AT, где AT = 0,1 ms — шаг считывания. График зависимости относительной ошибки от отношения сигнал/шум приведен на рисунке 6.

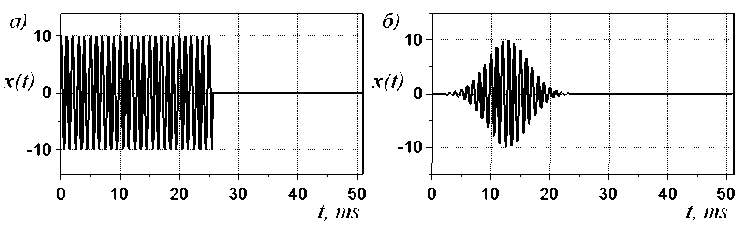
Рис. 5. Радиосигналы с прямоугольной (а) и гауссовой (б) огибающей на входе схемы радиоимпульсного стробирования

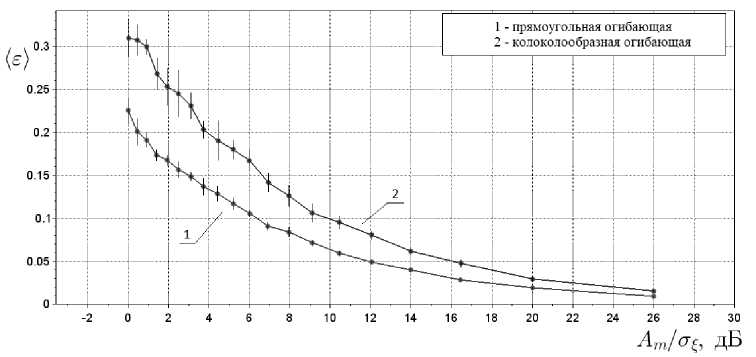
Рис. 6. Зависимость относительной ошибки воспроизведения от отношения сигнал/шум для радиосигналов с прямоугольной (1) и гауссовой (2) огибающей

Исследование помехоустойчивости модели стробоскопического преобразователя при работе с когерентной последовательностью сложных сигналов проводилось на примере радиосигнала с линейной частотной модуляцией (ЛЧМ-сигнала). Вид сигнала приведен на рисунке 7.

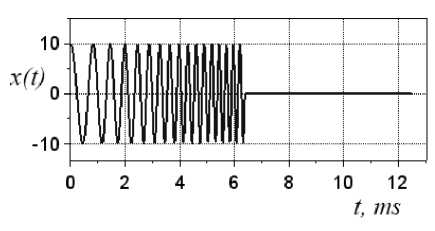
Рис. 7. ЛЧМ-радиоимпульс на входе стробоскопического преобразователя

В данной работе математическая модель ЛЧМ-радиосигнала и стробирующего импульса описывается соотношением (8). Исследуемый и стробирующий сигналы были выбраны одинаковыми, что имитирует работу корреляционного приемника РЛС [2]:

x(t) =

A(t) cos ^0t +--t²^

где A(t) — прямоугольная огибающая ЛЧМ-радиоимпульса длительностью т _и .

Моделирование производилось на временном интервале t Е [0,NT ], девиация частоты составляла AF = 1, 63 kHz, а база сигнала ~ 10, 5. Результаты моделирования на фоне аддитивной помехи для ЛЧМ-импульса представлены на рисунке 8.

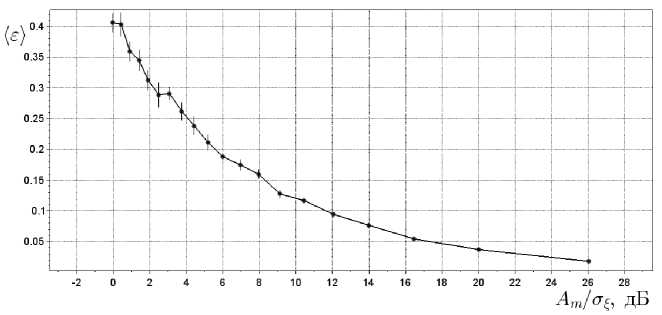
Рис. 8. Зависимость относительной ошибки воспроизведения ЛЧМ-радиоимпульса от отношения сигнал/шум

Заключение

В работе использована математическая модель стробоскопического преобразователя периодических сигналов, включающая в себя перемножитель и узкополосный фильтр. Методом численного моделирования произведен расчет погрешности воспроизведения видео- и радиоимпульсных сигналов на фоне белого гуссового шума.

В результате проведенных численных экспериментов показано, что нарушение синхронизации исследуемого и стробирующего сигналов в большей степени влияет на точность воспроизведения входных сигналов по сравнению с аддитивным шумом.

Полученные в поцессе моделирования результаты позволяют оценить допустимый уровень помех при стробоскопической обработке широкополосных импульсных радиосигналов на этапе проектирования радиотехнических систем.