Оценка процесса переноса энергии в тепловом накопителе с высокотемпературным рабочим телом при его разрядке

Хранение тепловой энергии является перспективной экологически чистой и энергосберегающей технологией с незначительными потерями тепла. Накопление перекачиваемой тепловой энергии играет ключевую роль в крупномасштабном сборе и использовании традиционных и возобновляемых ресурсов с присущими им свойствами, такими как непостоянство и нестабильность. Несоответствие между спросом и предложением энергии требует дополнительных исследований в области экономически эффективных и крупномасштабных технологий хранения энергии, ориентированных на получение экологически чистой энергии, которые могут эффективно устранить эти недостатки [1, 2]. Для компенсации пикового потребления требуется включение в состав систем теплоснабжения нако- пителей тепловой энергии [3, 4]. Аккумулирование тепловой энергии уже обладает широким спектром применений [5–8]. На сегодняшний день представлено множество концептуальных прототипов крупномасштабных накопителей энергии, которые в основном включают в себя явное хранение тепла, скрытое хранение тепла (накопление тепла с фазовым переходом) и термохимическое хранение тепла [9–12]. Таким образом, основной принцип накопления энергии сводится к процессу преобразования энергии из одной формы в другую, которую можно сохранять, а затем при необходимости преобразовывать обратно в ее первоначальную форму.

Актуальность исследования

Наиболее важным критерием при проектировании накопителей тепла является обеспечение надежности и безопасности энергоснабжения, которые обеспечиваются выбором рабочего тела на основе таких параметров, как теплопроводность, теплоемкость, коэффициент теплового расширения и др. [13, 14]. При этом любая система аккумулирования тепла требует надлежащей изоляции для предотвращения тепловых потерь и обеспечения долгосрочного хранения энергии [15, 16]. Таким образом, актуальной темой исследования является анализ эффективности теплоизоляционных конструкций, покрывающих тепловой накопитель, и их выбор при проектировании с точки зрения теплопередачи.

Постановка цели исследования

Целью данной работы является исследование процесса переноса энергии в тепловом накопителе при его разрядке. В непосредственные задачи исследования входило провести анализ материалов для системы аккумулирования тепловой энергии (высокотемпературного рабочего тела, теплоизоляционных материалов), разработка методики оценки разрядки теплового накопителя энергии.

В качестве рабочего тела предлагается использовать графит. Выбор этого материала обусловлен высокой теплопроводностью и стабильностью при повышенных температурах, что позволяет ему эффективно хранить большие объемы тепловой энергии (температура плавления графита составляет свыше 3600 °C) [17, 18]. Однако про- блемой при проектировании теплового накопителя является выбор тепловой изоляции, удовлетворительно работающей при температуре ~ 2000 °C. Использование традиционных теплоизоляционных материалов в качестве изоляции не представляется возможным из-за того, что температура плавления этих материалов обычно не превышает 1200 °C.

Научная новизна

Научная новизна заключается в разработке теплового накопителя энергии с использованием высокотемпературного рабочего тела для аккумулирования и последующего высвобождения тепловой энергии (рис. 1) и алгоритма оценки его разрядки в зависимости от характеристик эксплуатации. Результаты будут полезны для будущего развития теплоаккумулирующих систем и их оптимизации.

Рассмотрим основные элементы разработанного теплового накопителя энергии. Высокотемпературный жидкометаллический теплоноситель 1 предназначен для эффективной передачи тепловой энергии к рабочему телу 3 или от него. В качестве теплоносителя применяется олово, так как характеризуется низкой температурой плавления и высокой теплопроводностью [19]. Цилиндрический канал 2 изготовлен из высокоплавкого материала вольфрама (температура плавления вольфрама составляет свыше 3400 °C) с целью обеспечения долговечности и целостности структуры при высоких

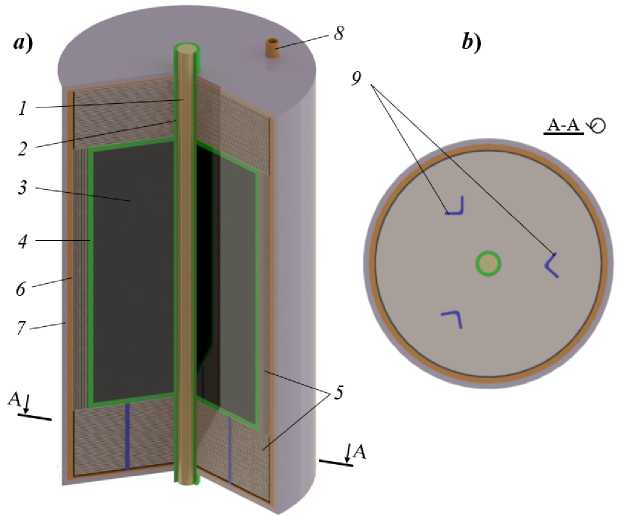
Рис. 1. Принципиальная схема теплового накопителя энергии: a – с многоступенчатым разрезом, b – с наклонным разрезом через плоскость сечения A-A : 1 – высокотемпературный жидкометаллический теплоноситель; 2 – цилиндрический канал; 3 – твердотельный теплоаккумулятор; 4 – контейнер; 5 – экраны; 6 – корпус; 7 – теплоизоляция;

8 – патрубок; 9 – опорные элементы

Fig. 1. Schematic diagram of a thermal energy storage device: a – with a multistage section, b – with an inclined section through the section plane A-A : 1 – high-temperature liquid metal coolant; 2 – cylindrical channel; 3 – solid–state heat accumulator; 4 – container; 5 – screens;

6 – casing; 7 – thermal insulation; 8 – flange; 9 – support elements

температурах. Твердотельный теплоаккумулятор 3 из графита предназначен для хранения тепловой энергии. Контейнер хранения теплоаккумулятора 4 выполнен из вольфрама и служит для защиты и хранения графита. Для минимизации тепловых потерь контейнер 4 помещается в систему теплоизоляции, состоящую из двух контуров: первый – экраны из вольфрама 5 , второй – минеральная вата 7 .

Вольфрам является эффективным барьером для радиационных потерь в дополнение к его способности функционировать при высоких температурах ввиду его высокой плотности и металлических свойств, которые способствуют значительному отражению и поглощению теплового излучения. Для укрепления конструктивной прочности теплового накопителя энергии между теплоизоляционными контурами устанавливается металлический корпус 6 . В верхней части теплового накопителя энергии размещен патрубок 8 , предназначенный для удаления воздуха и закачки в него аргона.

Применение аргона обосновано тем, что он препятствует химической реакции между графитом и кислородом, тем самым способствуя стабильности и продолжительности эксплуатации теплового накопителя. При достижении температуры свыше 400 °C графит в условиях кислородсодержащей атмосферы подвергается окислительному процессу, что приводит к его постепенной деградации и утрате теплопроводных характеристик [20]. Выделяющийся в процессе окисления графита углекислый газ снижает объем активного материала, сохраняющего тепло, и повышает риск потери герметичности и структурной целостности накопителя энергии.

В качестве второго контура теплоизоляции теплового накопителя энергии 7 используем минеральную вату, так как она обладает низкой теплопроводностью и высокой термостойкостью, кроме того, является сравнительно недорогой среди других материалов.

В нижней части разработанного устройства располагаются опорные элементы 9 , позволяющие его устанавливать вертикально.

Принцип действия накопителя основан на том, что избыточная энергия может быть эффективно задействована для нагрева олова 1 до температуры 2000–2500 °C с помощью трубчатого электронагревателя. Протекая в цилиндрическом канале 2, олово передает тепло графиту 3, который аккумулирует ее. Учитывая, что олово находится в твердом состоянии при температуре ниже 232 °C, необходимо применение магнитогидродинамических (МГД) насосов для обеспечения его циркуляции. В моменты, когда сеть испытывает дефицит электроэнергии, инициируется обратный процесс: нагретое олово проходит через тепловой накопитель энергии, отбирая тепловую энергию от графита, и далее направляется в систему, интегриро- ванную с МГД-генератором, который преобразует тепловую энергию обратно в электрическую, позволяя таким образом устранять дефициты мощности в энергосистеме. Такая конфигурация обеспечивает не только повышенную надежность энергоснабжения, но и способствует более эффективному использованию возобновляемых источников энергии.

Методы исследования

Решение поставленных задач осуществляется на основе исследования процесса теплопередачи через теплоизоляционные контуры теплового накопителя энергии.

Модель циклически работающего теплового накопителя энергии можно представить в виде упрощенной схемы (рис. 2) для разработки методики оценки его разрядки. При ее разработке были приняты следующие допущения: 1) процесс является стационарным, 2) размеры канала с оловом считаются пренебрежимо малыми, 3) температура на внешней поверхности графита принималась постоянной, 4) тепловой поток от графитового твердотельного теплоаккумулятора распределяется равномерно в осесимметричном направлении.

Для получения расчетных результатов задавались следующие начальные параметры: радиус и высота теплового накопителя энергии – 0,125 и 0,25 м соответственно; общая толщина каждого слоя первого теплоизоляционного контура, представляющего собой экран из вольфрама толщиной 0,9 мм и аргоновую прослойку газа толщиной 0,1 мм, составляла 1 мм.

На первом этапе осуществлялся расчет геометрических размеров системы теплоизоляции теплового накопителя энергии по выражениям (1)–(13). На данном этапе базовыми параметрами являются тепловой поток Q = 800 Вт, подводимый к графиту, и температура наружной стенки графита t _1.0 = 2000 °C. Искомыми параметрами являются толщины двух контуров системы теплоизоляции и расчет температурного поля.

Ввиду того, что теплообмен в накопителе энергии протекает при высоких температурах, необходимо учитывать все его виды. В таком случае расчет толщины теплоизоляции и температурного поля в накопителе энергии представляет собой задачу многослойной цилиндрической стенки, чем осложняется. В частности, необходимо учесть разделение заданного теплового потока ( Q = 800 Вт), проходящего через каждый теплоизоляционный слой накопителя энергии, на три составляющие (кондуктивный Q_T , конвективный Q_C и лучистый Q R теплообмен). Каждая расчетная формула для соответствующего теплового потока содержит температуры на границах рассчитываемого слоя теплоизоляции. В результате данная задача в явном виде решена быть не может. Таким образом, расчет геометрических размеров системы тепло-

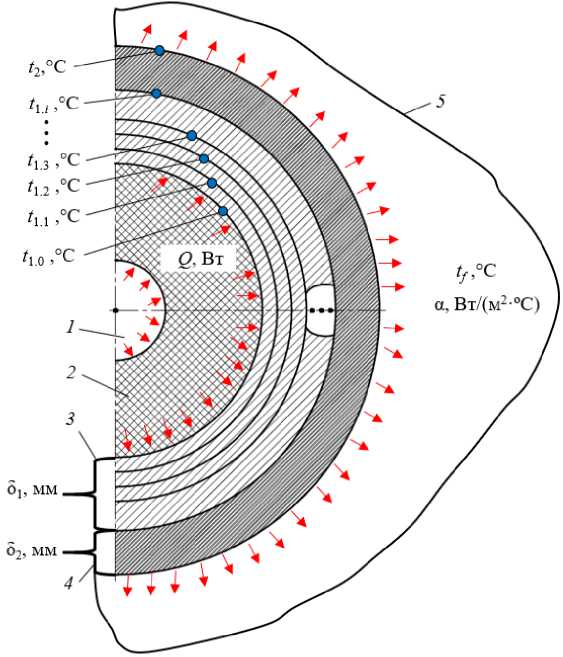
Рис. 2. Упрощенная схема циклически работающего теплового накопителя энергии с высокотемпературным рабочим телом: 1 – высокотемпературный жидкометаллический теплоноситель; 2 – твердотельный теплоаккумулятор; 3 – первый теплоизоляционный контур; 4 – второй теплоизоляционный контур; 5 – окружающая среда Fig. 2. Simplified diagram of a cyclically operating thermal energy storage device with a high-temperature working fluid: 1 – high-temperature liquid metal heat transfer fluid; 2 – solid-state heat accumulator; 3 – first thermal insulation layer; 4 – second thermal insulation layer; 5 – surrounding environment

изоляции накопителя энергии осуществляется методом приближений (итерационным расчетом).

Упрощенный алгоритм расчета представлен на рис. 3.

При расчете каждого слоя теплоизоляции первого контура задавалось итерационное значение разницы температур ΔT между соседними стенками, равное 1 °C с шагом 1 °C (шаги 2–4). Стоит отметить, что температура одной из стенок, расположенной ближе к графиту, является известной. Например, для первого слоя теплоизоляционного контура данная температура равна t1.0 = 2000 °C. Вводимое приближенное значение ΔT позволяет рассчитать температуру второй стенки t1.1. Далее вычисляется расчетный тепловой поток Q (шаг 5), состоящий из кондуктивного, конвективного и лучистого по формуле (11). После чего осуществляется проверка соответствия расчетного теплового потока с базовым значением (шаг 6) и вычисляется неопределенность между ними, которая должна составлять менее 5 %. В ином случае расчет теплоизоляционного слоя осуществляется заново с увеличением ΔT на 1 °C (итерационный процесс) (шаг 7). Таким образом, проводится рас- чет каждого слоя теплоизоляции первого контура и определяется их количество (шаг 10). Расчет его толщины завершается в том случае, если температура последнего теплоизоляционного слоя составляет менее 900 °C (шаг 9), что позволяет использовать классические теплоизоляционные материалы более экономически выгодные, например, минеральную вату.

Следующим шагом является итерационный расчет толщины второго теплоизоляционного контура (шаг 11). На первой итерации толщина принимается равной 0,1 мм (шаг 12). Далее (шаг 13) рассчитывается температура на внешней стенке второго теплоизоляционного контура t 2 , которая должна быть равна значению из диапазона от 50 до 350 °C (шаг 14). В ином случае расчет толщины второго теплоизоляционного контура осуществляется заново с увеличением δ 2 на 1 мм (итерационный процесс) (шаг 15). Далее рассчитывается коэффициент теплоотдачи и расчетный тепловой поток Q ₃ (шаг 16), который сравнивается с базовым значением (шаг 17). При неопределенности между потоками более 5 % осуществляется переход к следующей итерации (шаг 15).

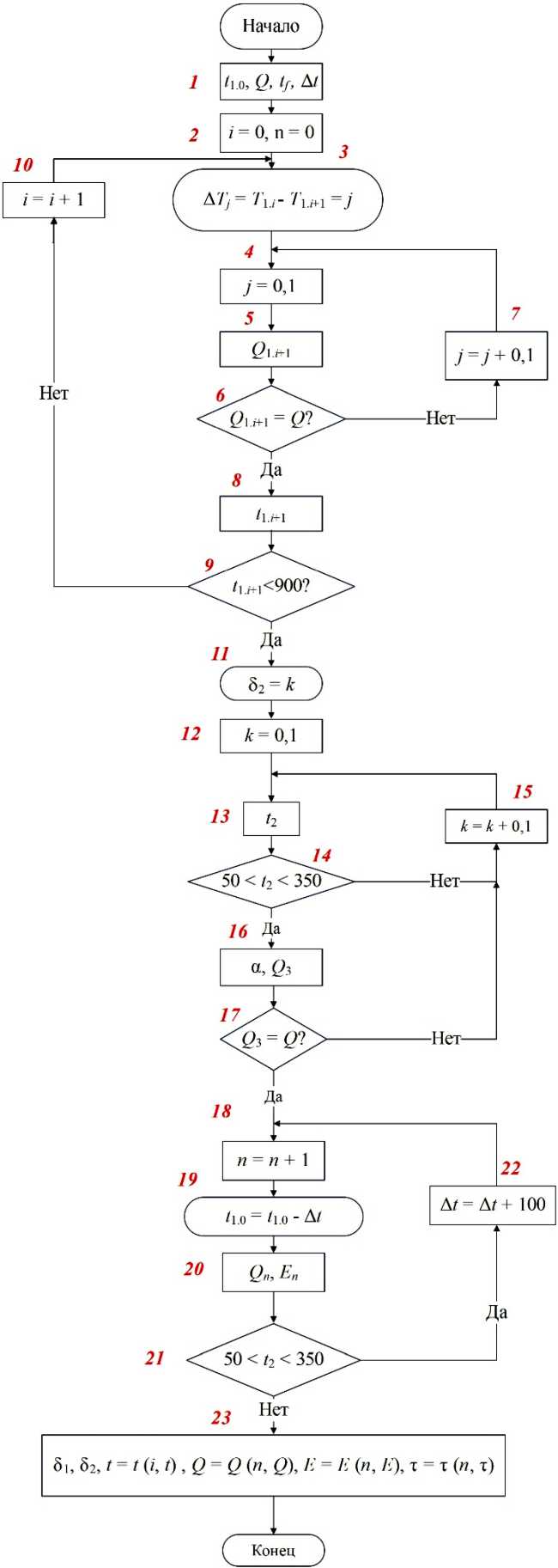
Рис. 3. Алгоритм оценки разрядки теплового накопителя энергии

Fig. 3. An algorithm for evaluating the discharge of a thermal energy storage device

На втором этапе рассматривается процесс разрядки теплового накопителя энергии с высокотемпературным рабочим телом. Данный подход реализуется путем расчета и сравнения между собой нескольких стационарных режимов работы теплового накопителя, характеризующихся различной температурой t _1.0 , которая для каждого последующего режима понижается с заданным шагом Δ t = 100 °C. При этом базовые значения теплового потока Q переопределяются. Используя рассчитанные значения хранимой энергии на различных стационарных режимах, можно оценить потери энергии при каждом шаге понижения температуры на Δ T и оценить время разрядки устройства по выражениям (14) и (15) соответственно (шаги 18–20). Итерационный расчет завершается в тот момент времени, при котором температура наружной стенки накопителя энергии t ₂ принимает минимальное допустимое значение (шаг 21).

Расчетный тепловой поток, проходящий через каждый слой первого теплоизоляционного контура, вычислялся по выражению

Q 1.i = Q R ( 1. i ) + Q T ( 1. i ) + Q C ( 1. i ) , ⁽¹⁾

где ε i +1 – коэффициент излучения вольфрамовой стенки ( i + 1)-го слоя.

Кондуктивный тепловой поток вычислялся по формуле

Q T ( 1. i )

^{2 n} h ^ f ( t 1i ^— t 1i + 1 )

ln r + 1

ri

где i – порядковый номер теплоизоляционного слоя (см. рис. 2).

Лучистый тепловой поток Q_R (_{1. i} ) :

где h – высота вольфрамовой стенки, м; λ f – коэффициент теплопроводности аргона, Вт/(м·°C); t 1. i – абсолютная температура вольфрамовой стенки i -го слоя, °C; T _{1. i +1} – температура вольфрамовой стенки ( i + 1)-го слоя, °C, r_i и r_{i +1} – радиус вольфрамовой стенки i -го и ( i + 1)-го слоя соответственно, м.

Из-за ограниченности замкнутого пространства, в котором осуществляется переда тепловой энергии (между слоями первого теплоизоляционного контура), конвективный теплообмен рассматривается условно. Для его расчета применяется формула (6), где перенос тепла происходит посредством теплопроводности, в которой вводится эквивалентный коэффициент теплопроводности λ e , Вт/(м·°C), вычисляемый по формуле

^ e = S k ^ f , (7)

Q r ( i i ) = C i — i + 1 Ft

—

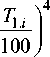
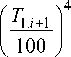
Ф ,

где С_{i - i +1} – коэффициент взаимного излучения, Вт/(м²·К⁴); F_i – поверхность излучения, м²; T _{1. i} – абсолютная температура вольфрамовой стенки i -го слоя, К; T _{1. i +1} – абсолютная температура вольфрамовой стенки ( i + 1)-го слоя, К; φ – средний угловой коэффициент, определяемый формой и размерами участвующих в теплообмене поверхностей,

где εk – коэффициент конвекции, принимаемый равным 1 при GrPr < 1000, или при GrPr > 1000, определяемый по формуле ek = 0,18 (GrPr )0,25,                          (8)

где Pr – число Прандтля, Gr – число Грасгофа рас-

считываем по выражению

Gr =

gh ³P( F t 1i + 1 )

v ²

,

их взаимным расположением и расстоянием меж-

где g – ускорение свободного падения, м/с²; ν – коэффициент кинематический вязкости, м²/с; β – температурный коэффициент объемного расширения, рассчитываемый по выражению, 1/К:

ду ними.

Коэффициент взаимного излучения вычислялся по формуле

в =

.

273 + t 1. i + 1

C / — / + 1

1     F i ( J1_

C⁺F + 1 1 C + 1 C o

Таким образом, выражение (1) может быть преобразовано к виду

Q 1. i = Q r (m) +S _kQ T ( 1.i ) .                       (11)

где C_i и C_{i +1} – коэффициент излучения вольфрамовой стенки i -го и ( i + 1)-го слоя соответственно, Вт/(м²·К⁴); F_{i +1} – поверхность излучения, м²; C ₀ – коэффициент лучеиспускания абсолютного черного тела, Вт/(м²·К⁴).

Коэффициент излучения вольфрамовой стенки i -го теплоизоляционного слоя рассчитывается по выражению

C i = C qS / ,                                       (4)

где ε _i – коэффициент излучения вольфрамовой стенки i -го слоя.

Коэффициент излучения вольфрамовой стенки ( i + 1)-го теплоизоляционного слоя:

Тепловой поток Q ₂ , проходящий через второй теплоизоляционный контур из минеральной ваты, равен кондуктивному. Тогда расчетное выражение будет выглядеть следующим образом:

Q 2 =

^{2 n} h ^ ( t 1.i ^— t 2 )

r ln ^rm

r 1. i

^C i + 1 = ^C 0 ^s i + 1 ,

где λ – коэффициент теплопроводности минеральной ваты, Вт/(м·°C); r m – наружный радиус стенки минеральной ваты, м.

Тепловой поток Q 3 от наружной стенки второго теплоизоляционного контура к окружающей среде вычислялся по уравнению

Q 3 = F m a ( 1 2 — t f ) , (13)

где F m – площадь наружной стенки из минеральной ваты, м²; α – коэффициент теплоотдачи от наружной стенки накопителя энергии к внешней среде, Вт/(м²·°C); t f – температура внешней среды, °C.

В выражении (13) коэффициент теплоотдачи α может быть вычислен по эмпирической формуле (14), которая справедлива для расчета теплоотдачи в закрытом помещении и является применимой при рабочих температурах от 50 до 350 °C.

Как было отмечено ранее, рассматриваемый процесс переноса тепловой энергии принимается стационарным. Исходя из этого, полная хранимая тепловая энергия в теплоаккумуляторе может быть рассчитана по выражению

E = mC p t io , (14)

где m – масса графитового твердотельного тепло-аккумулятора, кг; C p – изобарная теплоемкость графита, Дж/(кг·°C).

При изменении температуры t1.0 наступает другой стационарный режим. Таким образом, по формуле (14) можно вычислить хранимую энергию в теплоаккумуляторе для нового режима. Следовательно, оценочное время разрядки тепло- вого накопителя энергии можно вычислить на ос- нове сравнения двух стационарных режимов:

т =

E n - E n + 1 0,5 ( Q n + Q n + 1 ) ^,

где E n и E n +1 – хранимые тепловые энергии в тепловом накопителе при различных стационарных режимах, Дж; Q n и Q n +1 – тепловые потоки, соответствующие различным стационарным режимам, Вт.

Результаты исследований

На основе разработанного алгоритма были рассчитаны геометрические размеры двух теплоизоляционных контуров теплового накопителя энергии, значения которых составили δ1 = 0,139 и δ2 = 0,016 м. Уменьшение температуры графитового твердотельного теплоаккумулятора с шагом Δt = 100 °C для выявления различных стационарных режимов осуществлялось при температуре от 2000 до 700 °C, при которых базовый тепловой поток Q был равен от 800 до 172 Вт. При температуре менее 700 °C выражение (13) не может быть использовано, так как температура наружной стенки теплового накопителя составляет менее 50 °C (рис. 4). Сравнение различных стационарных режимов позволило оценочно установить, что за 72 ч тепловой накопитель энергии разряжается до 26,7 % (рис. 4, 5), при этом температура теплоаккумулятора уменьшается от 2000 до 700 °C.

Анализ доли тепловых потерь в тепловом накопителе энергии показал, что при высоких температурах передача тепла обусловлена преимущественно лучистым теплообменом (рис. 6–8). По мере удаления от графита, т. е. снижения температуры теплоизоляционных слоев первого контура, доля тепловых потерь радиацией уменьшается, а конвекцией, оцениваемой через эквивалентный коэффициент теплопроводности по выражениям (7) и (11), – увеличивается.

В ходе расчетов получена экспоненциальная зависимость температуры наружной стенки теплового накопителя энергии от времени его работы со средним квадратичным отклонением 0,99:

1 2 = 122 e ^{- 0,013 т} . (16)

Также получено выражение для оценки доли остаточного заряда теплового накопителя энергии от времени его работы со среднеквадратичным отклонением 0,99:

E+- = 0 ₉₇ e " "18^{: E} n ^,

.

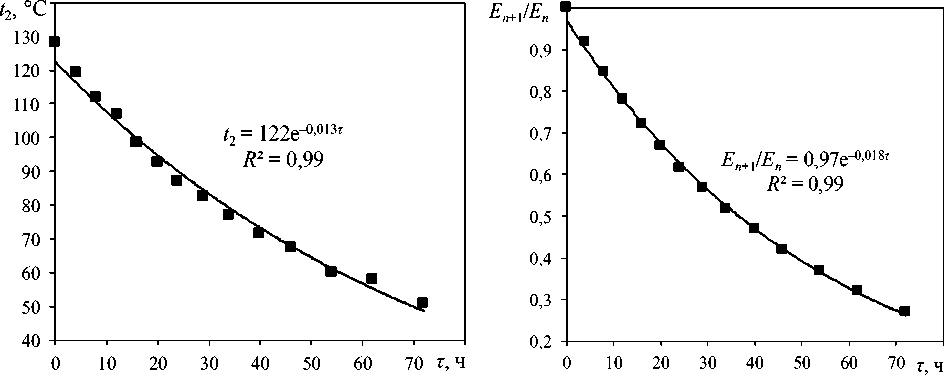
Рис. 4. Зависимость температуры наружной стенки теплового накопителя энергии от времени его работы

Fig. 4. Dependence of the temperature of the outer wall of the thermal energy storage on the duration of its operation

Рис. 5. Зависимость доли остаточного заряда теплового накопителя энергии от времени его работы

Fig. 5. Dependence of the proportion of residual charge of the thermal energy storage on the duration of its operation

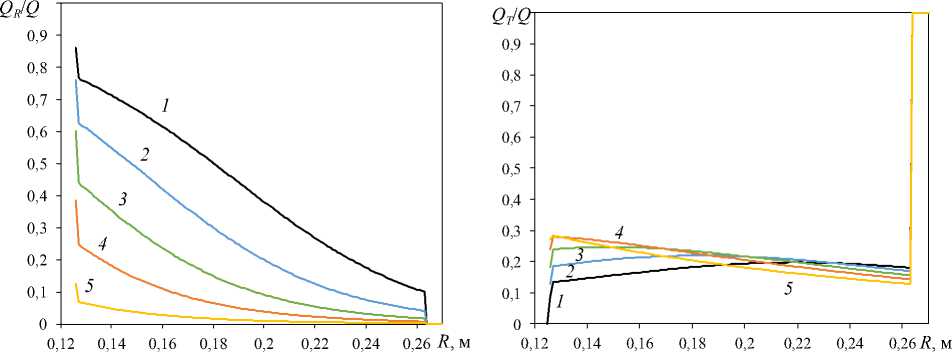
Рис. 6. Зависимость доли тепловых потерь излучением в теплоизоляции накопителя энергии радиусом R при различных стационарных режимах, характеризующихся температурой графита t 1.0 , °C: 1 – 2000; 2 – 1700; 3 – 1400;

4 – 1100; 5 – 700

Fig. 6. The dependence of the share of thermal losses by radiation in the thermal insulation of an energy storage device with radius R under various stationary conditions characterized by graphite temperature t 1.0 , °C: 1 – 2000;

2 – 1700; 3 – 1400; 4 – 1100; 5 – 700

Рис. 7. Зависимость доли тепловых потерь теплопроводностью в теплоизоляции накопителя энергии радиусом R при различных стационарных режимах, характеризующихся температурой графита t 1.0 , ºC: 1 – 2000;

2 – 1700; 3 – 1400; 4 – 1100; 5 – 700

Fig. 7. The dependence of the share of thermal losses by thermal conductivity in the thermal insulation of an energy storage device with radius R under various stationary conditions characterized by graphite temperature t 1.0 , °C: 1 – 2000;

2 – 1700; 3 – 1400; 4 – 1100; 5 – 700

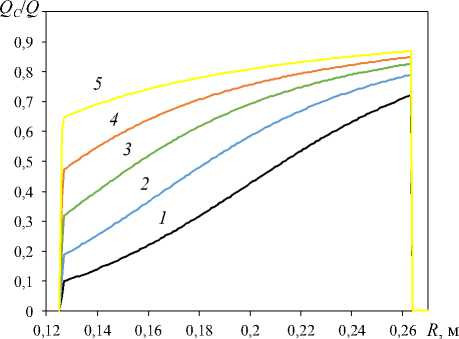
Рис. 8. Зависимость доли тепловых потерь конвекцией в теплоизоляции накопителя энергии радиусом R при различных стационарных режимах, характеризующихся температурой графита t 1.0 , °C: 1 – 2000; 2 – 1700; 3 – 1400; 4 – 1100; 5 – 700

Fig. 8. The dependence of the proportion of thermal losses by convection in the thermal insulation of an energy storage device with radius R under various stationary conditions characterized by graphite temperature t 1.0 , ºC: 1 – 2000; 2 – 1700; 3 – 1400; 4 – 1100; 5 – 700

Резкое уменьшение потери тепла при радиусе теплового накопителя R = 0,126 м обусловлено различием степени черноты графита и вольфрамовой фольги. Это приводит к значительному отличию теплопотери в системе «графит – экран» (на стыке графита и первого теплоизоляционного слоя) от системы «экран – экран» в первом теплоизоляционном контуре. При стационарном режиме, характеризующемся температурой t 1.0 , равной 2000, 1700, 1400, 1100 и 700 °C, доля тепловых потерь излучением в теплоизоляции теплового накопителя составляет 0,86–0,09,

0,76–0,04, 0,6–0,02, 0,38–0,001 и 0,13–0,0002 соответственно (см. рис. 6).

Доля тепловых потерь теплопроводностью составляет в диапазоне от 0,1 до 0,3. Очевидно, что во втором теплоизоляционном контуре (минеральной вате) тепловые потери вызваны полностью кондуктивным теплообменом (см. рис. 7).

Доля тепловых потерь конвекцией в слое аргона между экранами из вольфрама возрастает с понижением температуры в теплоизоляции в связи с уменьшением динамической вязкости газов. При температуре графита t 1.0 , равной 2000, 1700, 1400,

1100 и 700 °C, доля тепловых потерь конвекцией в теплоизоляции теплового накопителя составляет 0,049–0,72, 0,1–0,79, 0,21–0,82, 0,37–0,84 и 0,6–0,86 соответственно (см. рис. 8).

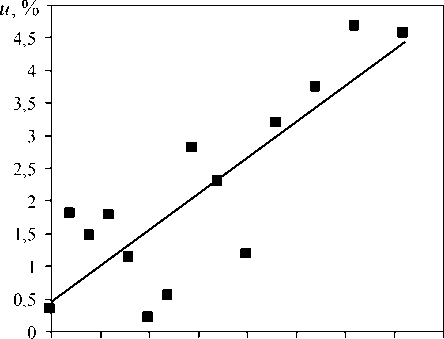
0    10   20   30   40   50   60   70 τ , ч

Рис. 9. Неопределенность итерационного расчета в различное время

Fig. 9. Uncertainty of the iterative calculation at different times

На основе анализа результатов расчета можно заключить, что допустимое отклонение до 5 % считается приемлемым показателем стационарности процесса (рис. 9). При снижении температуры графита ниже 700 °C наблюдается увеличение неопределенности итерационного расчета. Это связано с ограничениями применимости эмпирической формулы для расчета теплоотдачи от наружной поверхности теплоизоляции накопителя энергии к окружающей среде, которая актуальна для температурного диапазона от 50 до 350 °C.

Практическое значение

Разработанный алгоритм позволяет оценить геометрические размеры теплового накопителя энергии и прогнозировать время его разрядки с возможностью корректировки входных параметров. Это особенно значимо для систем, где требу- ется точная настройка на специфические условия эксплуатации, чтобы адаптировать систему под различные режимы работы.

Одним из ограничений текущего моделирования является использование формулы для оценки теплоотдачи от наружной стенки теплоизоляции к окружающей среде, применимой только при температурах от 50 до 350 °C. В связи с этим в перспективе планируется проведение физических экспериментов, что позволит уточнить и расширить применение текущей формулы. Это предоставит возможность оценить полную разрядку теплового накопителя энергии.

Выводы

На основе проведенного исследования можно сделать следующие выводы.

• 1.    Разработан алгоритм, позволяющий оценить геометрические размеры теплового накопителя энергии и время его разрядки. Получено, что при базовом значении теплового потока 800 Вт и температуре теплоаккумулятора 2000 °C толщина первого и второго теплоизоляционного контура составила 0,139 и 0,016 м соответственно.

• 2.    Сравнение различных стационарных режимов позволило оценочно установить, что за 72 ч тепловой накопитель энергии разряжается до 26,7 % (температура теплоаккумулятора падает от 2000 до 700 °C).

• 3.    Получены экспоненциальные выражения для описания уменьшения температуры наружной стенки и доли остаточного заряда теплового накопителя энергии от времени его эксплуатации.

• 4.    При высоких температурах доминирующим механизмом передачи тепла является радиационное излучение, доля которого постепенно уменьшается со снижением температуры теплоизоляционных слоев. С понижением температуры увеличивается доля конвективных потерь, оцениваемых через эквивалентный коэффициент теплопроводности.

• 5.    Представлены новые идеи для будущего развития теплового накопителя с графитом.