Оценка скорости турбулентного течения жидкости в трубопроводе на основе поверхностных измерений шума потока

В машиностроительной отрасли часто приходится иметь дело с пневматическим или гидравлическим приводом, с различного типа устройствами охлаждения или нагрева, в которых в силу иногда очень тяжелых условий эксплуатации требуется мониторинг основных параметров потока жидкой среды в трубопроводах и, в частности, температура и скорость потока. В то же время в области тяжелого машиностроения на разных принципах разрабатываются мощные силовые установки, в которых необходимо с высокой точностью контролировать температуру текущей с высокой скоростью охлаждающей жидкости, при этом установка врезных датчиков температуры в трубопровод нежелательна, а иногда и невозможна из-за резкого снижения эксплуатационных показателей. Все это требует, с учетом специфики машиностроительной отрасли, создания надежных неинтрузивных сенсоров, датчиков и методов измерений параметров потока в трубопроводах. Следует также отметить, что данная работа согласуется с поставленной правительством задачей на построение цифровой индустрии, где сенсорика, и в частности микросенсорика, является базисным элементом.

В работе рассматривается задача оценки скорости потока жидкости путем измерения интенсивности шума на поверхности трубопроводов [1], которые являются обязательными элементами гидросистем различного типа машин и механизмов. Данная задача необходима также для коррекции неинтрузивного измерения температуры потока в трубопроводе [2], так как распределение не только скорости, но и температуры зависит от величины средней скорости потока и определяет тем самым существенную часть погрешности поверхностных измерений температуры.

Известно, что источником шума в трубопроводе являются флуктуации скорости жидкости в турбулентном потоке, при этом для больших скоростей потока распределение средней скорости в поперечном сечении трубы достаточно равномерно и имеет логарифмический характер [3, 4], а общая температура потока близка к температуре в центре трубы. Однако при малых и умеренных скоростях потока, распределение температур неравномерно и составляющая от неравномерности может давать существенный вклад в общую погрешность измерений, особенно при поверхностных измерениях с помощью сравнительно точных термометров сопротивления. Очевидно, что для повышения точности неинтрузивных измерений температуры необходимо вводить поправку, являющуюся некоторой функцией средней скорости потока и способную компенсировать погрешность измерений от недостаточной степени однородности потока.

Требуется надежный и простой способ оценки скорости потока без внедрения в трубопроводную систему и непосредственно в поток, что само по себе может привести к появлению новых систематических погрешностей измерений. Необходимо выбрать такие характеристики шума турбулентного потока, которые бы могли определить его скорость; при этом требуется лишь оценочное значение, так как неоднородность потока медленно меняется в зависимости от величины средней скорости потока. Воспользуемся для решения этой задачи численным и натурным вариантом исследования.

1.    Выбор среды численного моделирования для расчета турбулентных потоков

Развитие вычислительной техники за последние годы в сочетании с развитием численных методов моделирования позволяют проводить расчеты сложных течений как внешней, так и внутренней гидродинамики трехмерных объектов.

Обычно используются осредненные по Рейнольдсу [5–8] уравнения Навье–Стокса (Reynolds-averaged Navier–Stokes, RANS) модели турбулентности (МТ), для замыкания которых используется совокупность дифференциальных уравнений, эмпирических и полуэмпирических соотношений. Также существуют модели, позволяющие непосредственно исследовать крупные вихревые структуры – метод крупных вихрей (LES), или же сразу все вихревые структуры – прямое численное моделирование (DNS). Однако их использование существенно ограничено из-за высоких вычислительных требований. Так, применение DNS основано на том, что уравнения Навье– Стокса правильно описывают как ламинарные, так и турбулентные течения, поэтому расчет турбулентных течений производится путем их непосредственного численного интегрирования, при этом должны использоваться, независимо от характера течения, трехмерные нестационарные уравнения Навье–Стокса, поскольку турбулентность является существенно трехмерной и нестационарной [9].

Кроме того, использование DNS требует достаточно точной оценки всех пространственновременных масштабов турбулентности. Наглядное представление об этих масштабах дает рис. 1, взятый нами из находящейся в свободном доступе работы [10], на котором изображен типичный энергетический спектр турбулентности при умеренных и высоких числах Рейнольдса.

Спектр содержит три области. Область I соответствует крупномасштабным «энергонесущим» вихрям с размерами порядка интегрального линейного масштаба L (ему соответствует

Численные методы моделирования

волновое число k I = 2π/L). В области III преобладают мелкие вихри с размерами поря д ка Колмогоровского η [9] и меньше с волновым числом k d = 2π/ η , вязкое трение в которых пер е водит кинетическую энергию турбулентности в тепло. Область II (инерционная область) спектра находится между областями I и III и содержит вихри с размерами L < l <  η . Влияние вязкос т и в области II отсутствует, и энергия турбулентности транспортируется от крупных к мене е крупным вихрям (энергетический каскад).

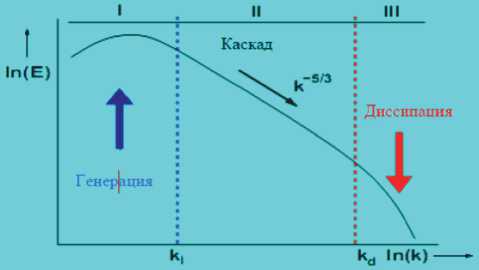
Рис. 1. Энергетический спектр турбулентного потока

Показано, что отношение максимального L и минимального η линейных масштабов турбулентности L/η пропорционально числу Рейнольдса в степени ¾, и в результате размер трехмерной сетки, нужной для расчетов с помощью DNS, растет как Re9/4, а суммарные затраты (с учетом нестационарности) на решение DNS увеличиваются с ростом числа Рейнольдса как Re11/4. Отметим, что рекомендуется иметь хотя бы 40 ячеек, расположенных в пограничном слое потока в радиальном направлении. Это делает затрудненным расчет турбулентных течений с большими числами Рейнольдса на основе самой точной DNS модели [9] в настоящее время и вынуждает использовать вспомогательные модели [6–8]. Не следует также забывать, что поставленная нами в этой работе задача имеет приближенный характер и не требует высокой точности вычислений, поэтому остановимся на двух широко используемых и существенно менее ресурсоемких k-ε и k-ω МТ [5, 7].

Стандартная k-ε модель зарекомендовала себя к ак устойчивая, экономичная и обладающая достаточной точностью для большого спектра задач. Применение в ней пристеночных функций дает возможность использовать численные модели с относительно невысоким разрешением вблизи стенок, получая при этом хорошие результаты. Вязкий подслой и переходная область пограничного слоя здесь не отыскиваются, а описыв а ются полуэмпирическими формулами (для кинетической энергии турбулентности k и скорости диссипации энергии турбулентности ε), что дает основание предполагать, что эту модель можно рассматривать как б азовую дл я решения различных прикладных задач.

На втором месте, скорее всего, стоит k-ω мо д ель. Основы этой модели были заложены А.Н. Колмогоровым [9], а ее реализация в вычислительной гидродинамик е выполнена Дэвидом Уилкоксом [11]. Стандартная k-ω МТ похожа на k- ε модель, но здесь уж е решается уравнение для скорости диссипации кинетической энергии турбулентности ω, что определяет требуемый характерный масштаб турбулентности.

Основным преимуществом k-ω МТ является то, что она обеспечивает хорошее описание пристеночных течений с большими градиентами давления и течений с отрывом пограничного слоя. К недостаткам относят более высокую степень нелинейности по сравнению с k-ε моделью, что отрицательно влияет на сходимость задачи.

Обобщая полученные данные, можно заключить, что в качестве среды моделирования, удовлетворяющей нашим сравнительно невысоким требованиям, можно выбрать любую вычислительную среду среднего класса, например Flow Simulation russian/SolidWorks/floxpress/, в которой течение в разных областях рассчитывается как турбулентное, ламинарное или переходное между этими состояниями. Реализованные в Flow Simulation двухмасштабные пристеночные функции (Two-Scales Wall Functions) позволяют реализовать два варианта расчета пограничного слоя в зависимости от значений параметров течения. Параметры турбулентности используются в качестве начальных и граничных условий на входе для внутренней задачи и внешних условий в случае решения внешней задачи. Кроме того, по умолчанию Flow Simulation генерирует параметры пограничного слоя у стенок на входах в модель. Тип пограничного слоя определяется в зависимости от числа Рейнольдса (определяется по эквивалентному гидравлическому диаметру входного отверстия, на котором и задается граничное условие: D = 4A/P, где A – площадь поперечного сечения отверстия, P – периметр отверстия). Толщина пограничного слоя находится по эффективной длине стенки, также зависящей от числа Рейнольдса.

Двухмасштабные пристеночные функции включа ю т два варианта расчет а погранич н ого слоя в зависимости от параметров течения. Модель «толстого пограничного слоя» используется для расчета пограничных слоев на подробной сетке (количество ячеек поперек пограничного слоя 6 и более). Модель «тонкого пограничного слоя» используется для расчета потока на грубой сетке (количество ячеек поперек пограничного слоя не превышает 4). Это может б ы ть течение в узких зазорах или цилиндрическое течение Куэтта. В случае перехода между толстым и тонким пограничными слоями используется комбинация этих моделей.

2.    Результаты численного моделирования

Итак, проводим расчеты в вычислительной среде Flow Simulation с настройками, учитывающими турбулентность, гравитацию и шероховатость внутренних стенок. В качестве текучей среды выбрана вода с температурами 20 и 80 °C, при этом тепловые граничные условия на стенке трубы адиабатические. Модель содержит прямолинейные участки трубопровода и два последовательных 90-градусных колена (рис. 2), определяющих стандартный тепловой компенсатор, на местных сопротивлениях которых эффект турбулентности существенно увеличивается.

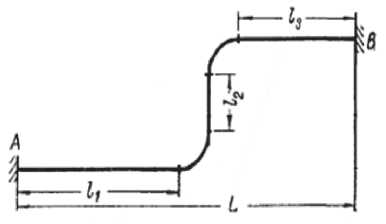
Рис. 2. Конфигурация трубопровода

Граничные условия на входе в прямолинейный участок трубы определяются нами или в виде массового расхода, или в виде скорости, а на выходе из трубопровода задается давление. Выбор в качестве граничного условия на входе скорости потока позволяет получить доступ к опциям «Задать параметры» и «Задать допол- нительные параметры» пограничного слоя, а именно: «Толщину динамического пограничного слоя», «Толщину теплового пограничного слоя», «Скорость на внешней границе пограничного слоя» и др. Это существенно увеличивает возможности расчета.

В качестве основного результата моделирования рассматривается величина удельной энергии турбулентности потока на заданном участке трубопровода. На рис. 3 и 4 представлены примеры расчетных распределений этой энергии с траекториями потока для расхода 0,05 и 0,1 кг/с в трубе ДУ50 при температуре 20 °C.

Очевидно, что энергия турбулентности максимальна у стенок в пограничном слое потока на боковой поверхности колена трубопровода. С ростом расхода жидкости вели ч ина удельной энергии достигает значений 4,4 ⋅ 10^–5 и 1,8 ⋅ 10^–4 Дж/K соответственно. Причина – влияние кривизны линий тока на турбулентность. На выпуклой стенке кривизна оказывает стабилизирую щ ее воздействие, а на вогнутой – дестабилизирующее. Это дает возможность определить мест о измерений – на боковой стороне колена, т. е. там, где достигается максимум энерги и , а значит, и максимум интенсивности шума турбулентности.

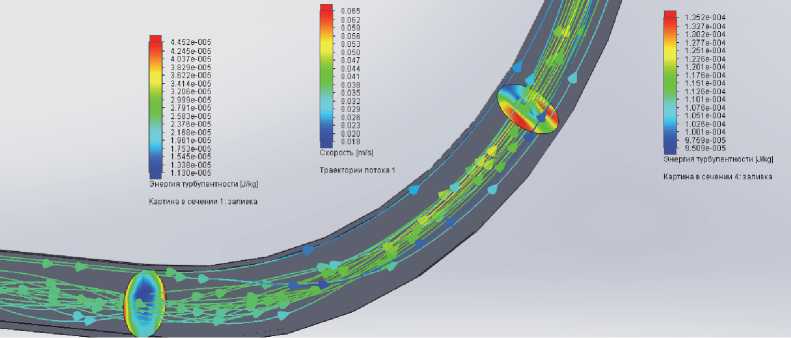
Рис. 3. Распределение удельной энергии турбулентности в начале и конце колена для расхода 0,05 кг/с

Численные методы моделирования

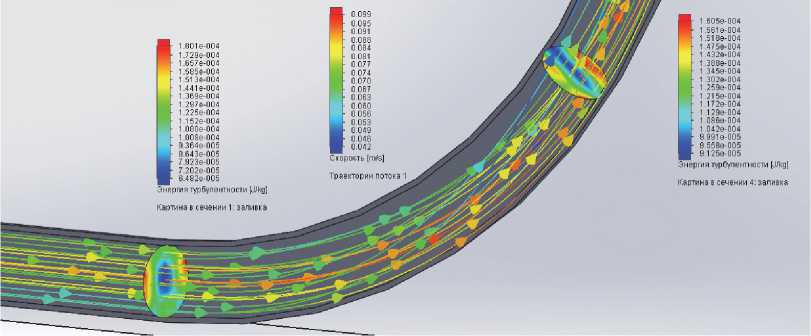
Рис. 4. Распределение удельной энергии турбулентности в начале и конце колена для расхода 0,1 кг/с

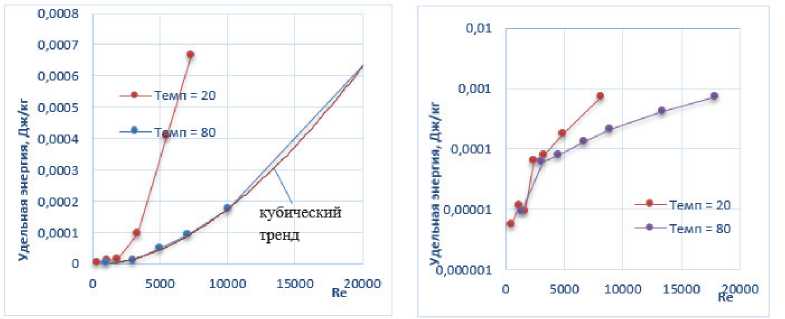
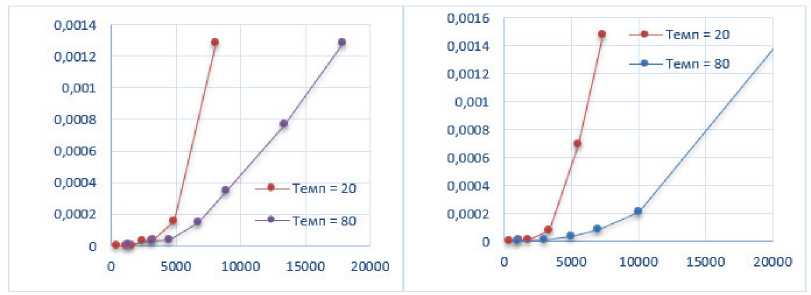
На графиках ниже (рис. 5 и 6) представлены зависимости удельной энергии турбулентности и диссипации удельной энергии в диапазоне чисел Рейнольдса 366…7320, что соответствует переходу от ламинарного потока к развитому турбулентному. Очевиден крутой характер этих зависимостей от числа Рейнольдса, причем с ростом температуры наклон характеристик падает, а значит падает и интенсивность турбулентного шума.

Чтобы аналитически определить характер этой зависимости и подтвердить тем самым корректность вычислений, воспользуемся работой Ландау [3], где делается такая оценка при помощи ряда упрощающих допущений.

а)                                                    б)

Рис. 5. Графики удельной энергии турбулентности для трубопровода ДУ50 (а) и ДУ80 (б) для двух расчетных температур потока 20 и 80 °С

а)                                                    б)

Рис. 6. Графики диссипации удельной энергии турбулентности для трубопровода ДУ50 (а) и ДУ80 (б) для двух расчетных температур потока 20 и 80 °С

Источником турбулентности является всегда некий внешний источник, затрачивающий определенную часть своей мощности на создание турбулентности, при этом в установившемся режиме эта мощность совпадает с энергией диссипации турбулентности в единицу времени и пропорциональна [3]:

ε _дисс ∼ u³/l, (1) где l – масштаб турбулентности, u – характерная средняя скорость турбулентного движения. В модели Ландау не делаются различия между скоростью турбулентного потока и скоростью турбулентных флуктуаций жидкости, так как полагается, что несжимаемая жидкость вне турбулентной области неподвижна, а сама турбулентная область является источником звука, распространение которого подчиняется волновому уравнению. На рис. 5, а представлен график кубического тренда

W = 2 ⋅ 10 ^{- 17}Re³ - 2 ⋅ 10 ^{- 12}Re² - 4 ⋅ 10 ^{- 10}Re + 2 ⋅ 10 ^{- 6}, (2) который согласуется с расчетной зависимостью при значении степени достоверности аппроксимации R² = 1, причем третья степень является минимальной для данной величины R². Это доказывает, что графики на рис. 5 и 6 согласуются с соотношением (1).

На рис. 5, б зависимость энергии турбулентности от числа Рейнольдса в отличие от рис. 5, а представлена в логарифмическом масштабе и показывает, что эта зависимость линейна, начиная со значений числа Рейнольдса Re ≈ 3000. Это позволяет рекомендовать логарифмические зависимости как энергии турбулентности, так и интенсивности турбулентного шума от скорости потока для создания линейной шкалы измерений в диапазоне умеренных и больших чисел Re. Полученные данные согласуются также с результатами моделирования других авторов [4, 12–16].

Показано, что количество энергии турбулентности, испускаемой в виде звука в единицу времени единицей массы турбулентной среды, пропорционально восьмой степени скорости турбулентного движения [3]:

ε зв ∼ u⁸/(c⁵ ⋅ l), (3) где c – скорость звука в жидкой среде.

Эти же величины определяют спектр мощности турбулентного движения жидкости, которая ограничена частотой fгр ∼u/l, (4) и такими же должны быть частоты в спектре акустического сигнала с длинами волн λ ∼ cl/u >> l, который мы и хотим определить.

Например, если масштаб турбулентности составляет 3 мм для трубы диаметром ДУ50, то для скорости водяного потока 5 м/с (Re = 249) при температуре 20 ° С характерная частота сигнала составляет f ≈ 1600 Гц. В аналогичных условиях и при скорости потока 55 м/c (Re = 2740) верхняя характерная частота сигнала уже составляет f ≈ 18300 Гц. Такие расчеты помогают определить, например, требования к датчику акустического сигнала, но являются чрезвычайно грубыми.

3.    Экспериментальное исследование

Исследование проводилось на проливном стенде ПГ Метран с целью установления частотных характеристик трубопровода при проливе воды в широком диапазоне расходов. В качестве датчика акустического сигнала использованы пьезопленочные датчики SDT1-028K (Measurement Specialties, Inc.), которые при сопротивлении на выходе 10 Мом обладают равномерной полосой пропускания 10 Гц…10 МГц и чувствительностью не хуже 2 % деформации.

Видим, что спектр сигнала на рис. 7 и 8 зависит от величины расхода, при этом с ростом расхода существенно расширяется полоса частот с мощными флуктуациями амплитуды сигнала в начальной зоне частот. Полученные зависимости отражают энергетический спектр турбулентного течения жидкости, так как деформация поверхности трубы с наклеенным на нее датчиком является следствием работы гидродинамических сил на ее упругих перемещениях.

Сравнивая рис. 7 и 8 с энергетическим спектром турбулентного потока на рис. 1, можно установить их подобие, в частности, на рис. 8 наглядно показано деление спектра на зоны c «энергонесущими» вихрями (зона I), инерционную (II) и диссипативную зону (III). Также важно отметить, что с ростом расхода расширяется полоса зоны I и несколько уменьшается величина амплитуд флуктуаций шума в ней.

Численные методы моделирования

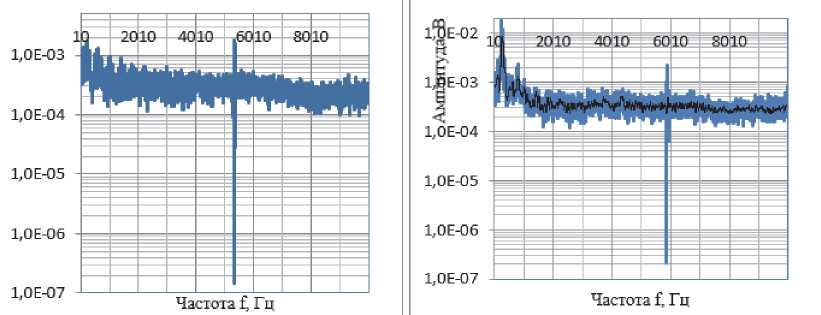
Рис. 7. Спектральная плотность сигнала пьезодатчика при расходе 0 (а) и 0,1 м3/с (б)

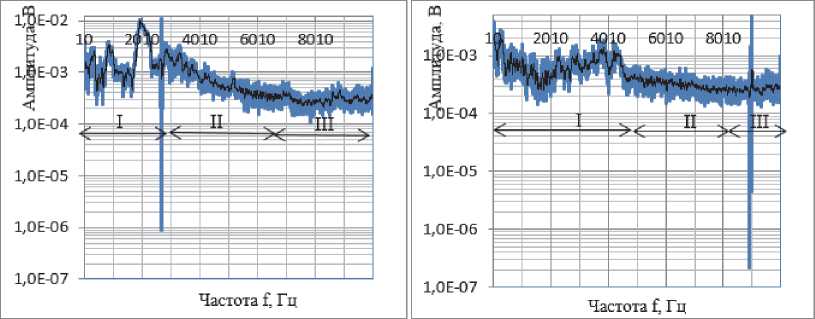
Рис. 8. Спектральная плотность сигнала пьезодатчика при расходе 0,5 (а) и 1 м3/с (б) с отображением характерных областей спектра

Из этого следует, что в качестве информационной величины можно выбрать, во-первых, ширину частотного промежутка зоны I, которая в соответствии с формулой (3) пропорциональна скорости потока (надо учитывать, что при изменении скорости может несколько меняться и масштаб турбулентности). Для получения информации о потоке можно использовать методы частотного детектирования [17–19]. Во-вторых, можно выбрать интегральное значение амплитуды сигнала датчика в полосе частот зоны I, но не будет большой ошибкой, если полосу частот интегрирования увеличить за счет включения частот зоны II и III, так как они мало интенсивны и не внесут больших искажений; при этом исчезает потребность точного определения полосы частот зоны I. Однако такое интегрирование спектральной плотности в частотной области трудно реализовать технически, поэтому можно перейти к временным сигналам, воспользовавшись формулой Рэлея [17, 20]:

∞∞

1 ∫ W( ω )d ω= ∫ a²(t)dt, ^π -∞            0

где W( ω ) – спектральная плотность энергии сигнала, ω – круговая частота сигнала, а(t) – измеряемый сигнал, t – время. Из выражения (5) следует, что для получения информации о средней скорости потока по интенсивности шума можно использовать квадратичное детектирование сигнала датчика, что делает реализацию такого подхода сравнительно простой задачей.

Выводы

В этой работе для оценки скорости турбулентного течения жидкости в трубопроводе использован численный и экспериментальный подходы. При численном моделировании турбулентного течения жидкости в трубопроводе использованы приближенные способы численного интегрирования пространственного уравнения Навье–Стокса с применением двухмасштабных пристеноч- ных функций вычислительной среды Flow Simulation. Это оправдано, учитывая приближенный характер наших вычислений.

Расчетами показано, что внутри потока зависимость энергии турбулентности описывается полиномом 3-й степени, при этом можно линеаризовать функцию измерений этой энергии при больших числах Рейнольдса, используя логарифмическую шкалу. Эти же выводы справедливы и для распространяемой внутри потока звуковой энергии, которая является частью энергии турбулентности и описывается уже волновым уравнением.

Для определения величины звуковой энергии на поверхности трубопровода использован экспериментальный подход, при этом выполнены измерения спектральной плотности акустического сигнала на поверхности трубопровода [21] проливного стенда. Показано, что получение информации о скорости потока возможно путем частотного детектирования ширины энергонесущей полосы частот спектра или квадратичного детектирования амплитудных значений акустического сигнала датчика.