Оценка сродства к электрону по данным о временах жизни отрицательных молекулярных ионов p-кумаровой и кумарин-3-карбоновых кислот

DOI:

Доктор физико-математических наук, профессор кафедры теоретической физики и волновых процессов, Волгоградский государственный университет ,

Германен является одним из ведущих перспективных 2D-материалов, имеющих структуру, аналогичную графену [7]. Обладая набором уникальных свойств [8], графен не лишен недостатков с точки зрения его интеграции в полупроводниковые устройства и преобразователи электромеханической энергии, такие как пьезорезистивные сенсоры, датчики давления, транзисторы, резисторы и многие другие. К примеру, у графена практически полностью отсутствует запрещенная зона энергий (Е _д < 0,05 мэВ), что не дает возможности закрытия канала полевого транзистора на его основе [8].

Германен, геометрическая структура которого была предсказана в 2009 г., а синтез осуществлен в 2014 г., является одним из самых перспективных наноматериалов «постграфеновой эры» [1]. Его запрещенная зона составляет в соответствии с теоретическими исследованиями величину Е _д ~ 24 мэВ, что на несколько порядков превышает графеновую. Это дает широкий спектр возможности управления его пьезорезистивными и проводящими свойствами. Способы управления можно внедрить путем внешней механической деформации наноматериала и допирования разнообразными дефектами замещения. Если объединить эти два фактора, то можно добиться вариабельного изменения свойств германена даже в ходе работы прибора на его основе.

В соответствии с поставленной научной задачей цель работы определяется как исследование пьезорезистивных свойств германеновых нанолент с изоморфными дефектами замещения, в качестве которых выбраны атомы кремния и олова. В научной литературе отсутствуют аналогичные расчеты, однако в процессе работы было проведено сравнение со свойствами примесных материалов похожей структуры.

1.    Описание модели

Структура энергетических зон деформированных нанолент (NR) описывается одномерным дисперсионным соотношением, получаемым из электронного спектра двумерного гексагонального слоя методом сворачивающихся зон. В рамках модельного подхода Хаббарда в приближении сильной связи и π-электронном приближении Хюккеля электронный спектр NR кресельного (индекс «a») и зигзагообразного (индекс «z») типов соответственно имеет следующий вид [5]:

e _a ( k ) = ± y ( 5)^ 1 ± 4cos ^^ cos [&Д ₀ (1 + 5)] + 4cos ² ^ ’

Е-z ( k ) = ± y ( 5 )

1 ± 4 cos [ kR 0 (1 + 5) ] cos ^ —L ^

+ 4 cos ² [ kR 0 (1 + 5) ] ,

где y ( 5 ) — интеграл перескока электрона между соседними атомами в деформированных нанолентах; 5 = △ R/R o — относительная деформация элементарной ячейки; R 0 — невозмущенная длина межатомной связи; к — продольная компонента волнового вектора в одномерной зоне Бриллюэна; q = 1,...п — поперечная дискретная компонента волнового вектора; п — число элементарных ячеек по ширине ленты.

Для описания энергетического спектра примесных германеновых нанолент используется модельный подход Андерсона, который подразумевает описание структур с предельно малыми концентрациями дефектов [2] и заключается в отдельном рассмотрении коллективизированных (π-электронов) и локализованных электронов. Взаимодействие между этими электронами учитывается посредством модельного параметра гамильтониана — потенциала гибридизации. Такая модель реализована для описания графеновых нанолент с точечными донорными и акцепторными дефектами замещения, однородно распределенными в кристаллической решетке наноматериала [9]. Зонная структура NR в модельном подходе Андерсона имеет следующий вид:

Е(к) = 2 [ez + е(К) ± У(е/ - e(k))2 + 36|VGeD(5) |2ж], где e(k) — электронный спектр наноленты без дефектов, описываемой соотношениями выше; е/ — энергетический уровень электрона на дефекте; ж = Nd/N — концентрация примесей; N — число элементарных ячеек в кристалле; Nd — количество дефектов в кристаллите; VceD(5) — потенциал гибридизации, представляющий собой матричный элемент энергии взаимодействия между электронами кристалла и точечного дефекта, как функция δ.

Примеси выбирались с учетом возможного изоморфного замещения атома германия элементами из IV группы: атомы кремния (Si) и олова (Sn). Для оценки энергии электрона на дефекте е _/ использовалась разность потенциалов ионизации атомов примеси и германия, которые отсчитывались от уровня Ферми:

е _/ = I _Ce — 1 st = 7, 88 эВ — 8,15 эВ = - 0, 27 эВ — для примеси кремния;

е _/ = I _Ce — I s™ = 7, 88 эВ — 7, 34 эВ = 0,54 эВ — для примеси олова.

Функциональная зависимость интеграла перескока y ( 5 ) и потенциала гибридизации V c _eD (5) от относительной деформации оценивались исходя из расчетов электронного строения германеновых нанолент с помощью метода теории функционала плотности с обменно-корреляционным потенциалом B3LYP в базисе атомных орбиталей STO-3G [6]. Квантово-химические расчеты электронного строения NRs осуществлялись для фрагмента поверхности германена размером 6 x 6 ЭЯ, в котором граничные ненасыщенные связи замыкались одновалентными атомами водорода. Атом точечного дефекта помещался в центр построенного кластера, чтобы уменьшить влияние граничных атомов водорода. Деформация структуры вдоль длины NR реализовывалась методом пошагового замораживания атомов германия на противоположных границах фрагмента. Рассчитанные функциональные зависимости y ( 5 ) и V _c eD(5) апроксимировались аналитическими выражениями экспоненциального вида:

Y = Y o exp(— 19523R), Y o = 171,11 эВ, R = R o (1 + 5),

V _GeD = V o exp(—18498R), V o (D = Si) = 132, 91 эВ, V o (D = Sn) = 175, 28 эВ .

Путем геометрической оптимизации геометрии построенного фрагмента германена методом теории функционала плотности получены длины межатомных связей недефор-мированного бездефектного германена, которые составили R 0 = 2,44 A. В расчетах использовались следующие значения деформации однородного растяжения (сжатия) в диапазоне 5 = — 0,1,... 0,1. Для нахождения продольной компоненты тензора эласто-проводимости M [2] в работах [3; 4] предложена следующая формула:

Ао1

М =--

σ0 σ где Ао = о — 00 — изменение удельной проводимости деформированного германена; σ и σ0 — проводимость деформированной и недеформированной наночастицы соответственно. Удельная продольная проводимость NR вычислялась в рамках теории Кубо — Гринвуда и модели Хаббарда с помощью метода функций Грина [2]. Итоговое выражение для продольной удельной проводимости NR, входящее в величину М, имеет следующий вид:

о = 2^iniv ^ ^ v(k)v(q) < nka > [< nqe > +5kq5ga(1 — < nka >)], где V — объем; кв — постоянная Больцмана; Т — абсолютная температура; e — элементарный заряд; k, q — двухкомпонентные волновые вектора в пределах зоны Бриллюена (ЗБ); а, в — спиновые индексы; v(k) = ▽Е(k)/1 — вектор скорости электрона в ЗБ; < П(ка) > — среднее число частиц в состоянии с волновым вектором к и спином а, выражаемое функцией Ферми — Дирака:

N e = ^(П к _а ). к,а

Поскольку примеси являются изоморфными, то число п-электронов в NR равно числу атомов в кристаллите. Для бездефектных NRs уровень химического потенциала полагался равным 0 эВ.

Методика расчета продольной компоненты тензора эластопроводимости апробирована в работах [3; 4; 9], посвященных исследованию пьезорезистивных свойств углеродных наноматериалов.

2.    Обсуждение результатов

На рисунках 1–6 приведены рассчитанные функциональные зависимости компоненты тензора эластопроводимости М от деформаций растяжения и сжатия 5 для проводящих и полупроводниковых германеновых нанолент различной ширины и геометрической конфигурации. На каждом рисунке изображены графики М (5) для различных концентраций дефектов обоих видов N _a = 1,10,100,1000,10 000. Линии на графиках соединяют расчетные точки для выявления характера изменения эластопроводимости. Расчеты проведены при температуре T = 300 K. В тексте и на рисунках использованы следующие обозначения кресельных и зигзагообразных нанолент разной ширины: m Arm, где m = 9, 10, 50, 100 ЭЯ и n Zg, где n = 9, 10 ЭЯ соответственно. Расчетная минимальная длина нанолент выбиралась размером L = 100 000 ЭЯ. При дальнейшем увеличении длины результаты расчета не изменялись.

а)

б)

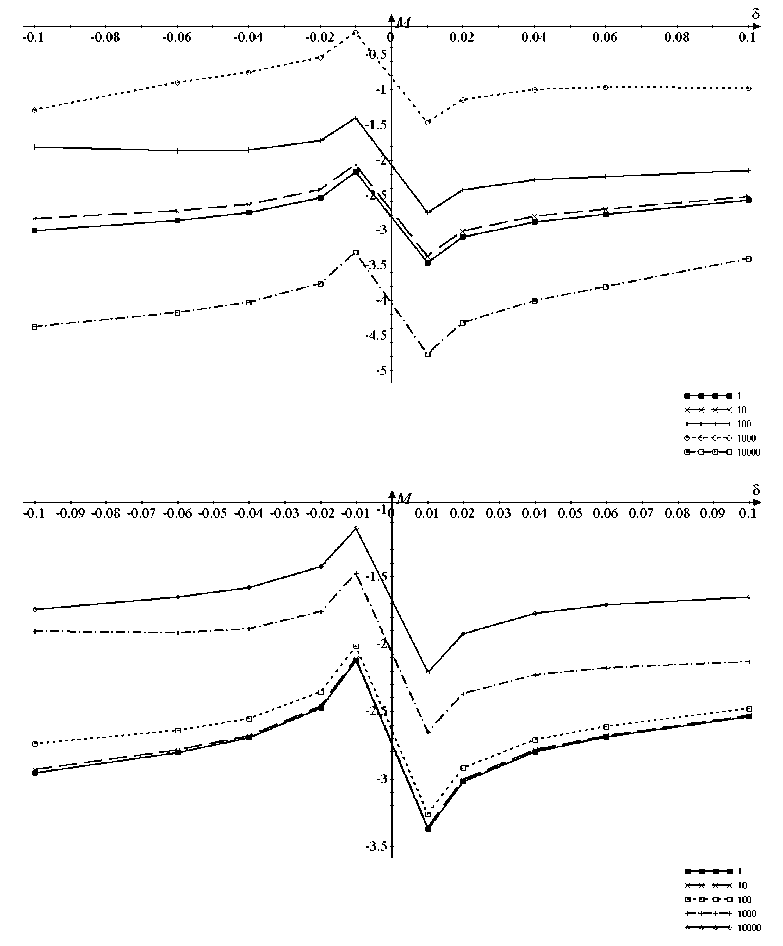
Рис. 1. Продольная компонента М тензора эластопроводимости проводящих 9 Arm GeNR как функция относительной деформации δ и концентрации дефектов атомов кремния ( а ) и олова ( б ) N _d = 1, 10, 100, 1000, 10 000

На рисунках 1, 5 и 6 наглядно продемонстрировано, что в случае проводящих нанолент типа 9 Arm, 9Zg и 10 Zg компонента М принимает отрицательные значения во всем диапазоне 5. Для деформаций сжатия (5 < 0) и растяжения (5 > 0) наблюдается монотонный рост функции М(5). Ее поведение полностью объясняют изменения в зонной структуре рассматриваемой деформированной наноленты. В области сжатия отрицательное значение M означает, что удельная проводимость увеличивается при деформации. Это следствие увеличения плотности состояний вблизи уровня Ферми, обусловленное уменьшением угла наклона дисперсионных кривых при сжатии ленты [ХФ]. Увеличение δ, в том числе и в диапазоне растяжения, соответственно увеличива- ет наклон кривых Е(к) и уменьшает плотность состояний в прифермиевской области. И как следствие, уменьшается удельная проводимость. Этот эффект связан с тем, что все большее число носителей заряда с все большими энергиями дает вклад в удельную проводимость кристаллита. Тепловые флуктуации приводят к заполнению электронами зоны проводимости NR согласно функции распределения Ферми — Дирака. Модификация электронного спектра ведет к изменению удельной проводимости, учитывающей все возможные заполненные электронные состояния, а, следовательно, к росту компоненты M с ростом величины δ.

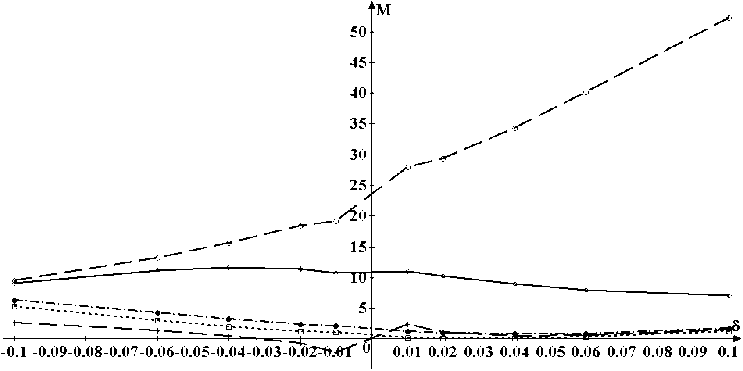
а)

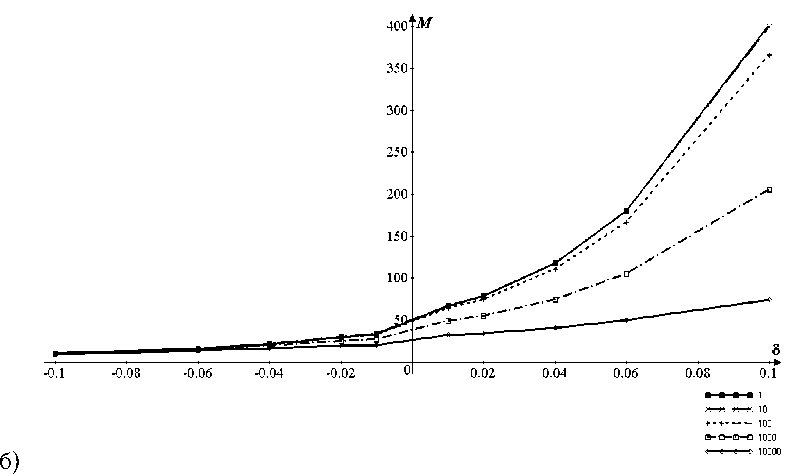
Рис. 2. Продольная компонента М тензора эластопроводимости полупроводниковых 10 Arm GeNR как функция относительной деформации δ и концентрации дефектов атомов кремния ( а ) и олова ( б ) N _d = 1, 10, 100, 1000, 10 000

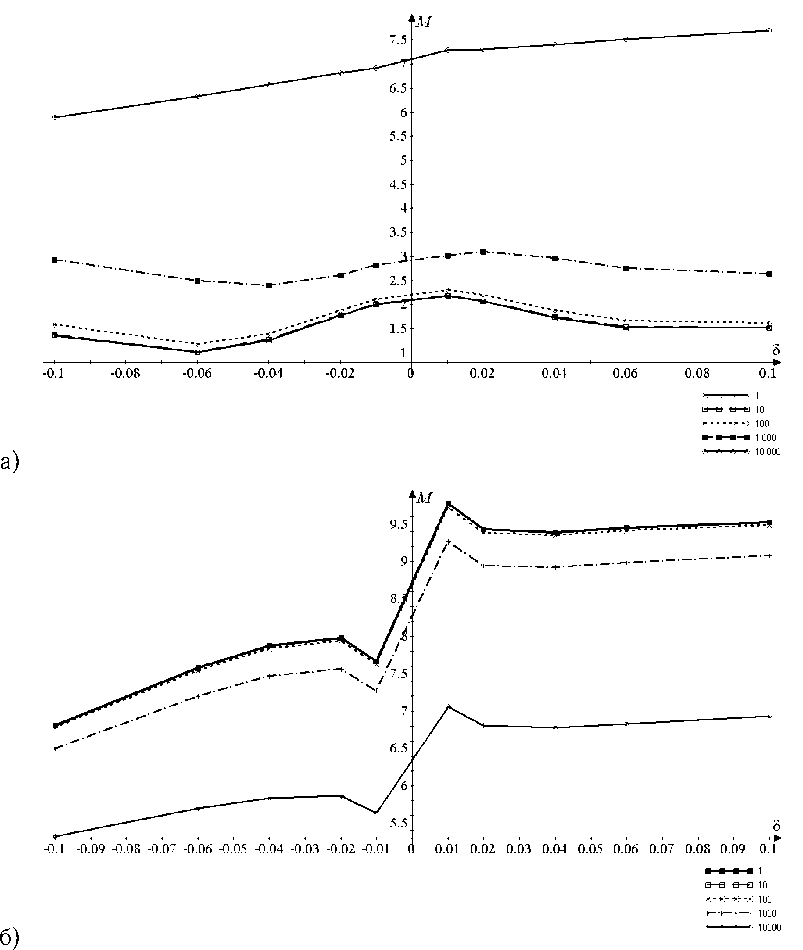
Рис. 3. Продольная компонента М тензора эластопроводимости полупроводниковых 50 Arm GeNR как функция относительной деформации δ и концентрации дефектов атомов кремния ( а ) и олова ( б ) N _d = 1, 10, 100, 1000, 10 000

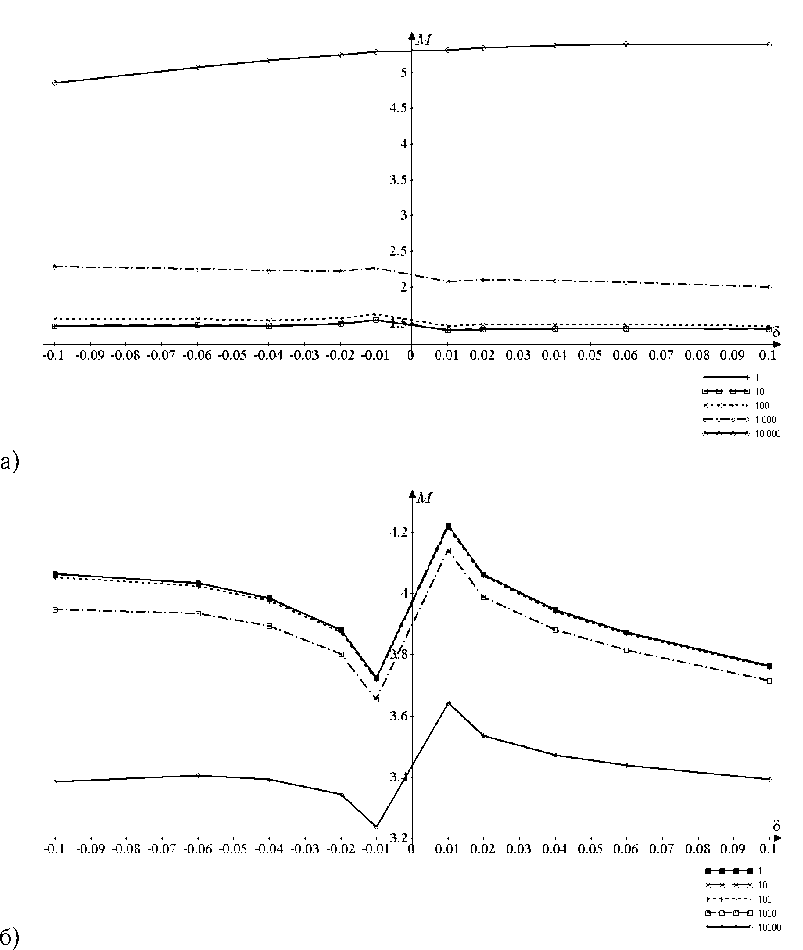
Рис. 4. Продольная компонента М тензора эластопроводимости полупроводниковых 100 Arm GeNR как функция относительной деформации δ и концентрации дефектов атомов кремния ( а ) и олова ( б ) N _d = 1, 10, 100, 1000, 10 000

Рост концентрации дефектов увеличивает численное значение величины М во всем диапазоне 5, не изменяя качественное поведение функций М (5). Таким образом, изоморфные дефекты, не изменяющие концентрацию и тип носителей заряда, увеличивают эластопроводимость и удельную проводимость нанолент. В этом эффекте проявляются два конкурирующих процесса — изменение плотности состояний вследствие деформации и изменение плотности состояний вследствие наличия примесей.

Разные типы дефектов (Si и Sn) не влияют на качественное поведение функций М(5), дают только количественное различие величины М. Единственное различие проявляется при больших концентрациях дефектов кремния Na = 10 000. Здесь график опускается ниже кривой с N = 1. Это связано с тем, что уровень электрона на дефекте близок к химическому потенциалу кристаллита (табл. 1). Рост концентрации атомов Si формирует примесную зону вблизи уровня е/, в которой присутствует энергетическая щель, также увеличивающаяся с ростом концентрации дефектов. Кроме того, примесная зона увеличивает плотность состояний вблизи уровня Ферми. Если уровень химического потенциала попадает в энергетическую щель примесной зоны, то проводимость кристаллита падает, что и наблюдается для кривой c N = 10 000.

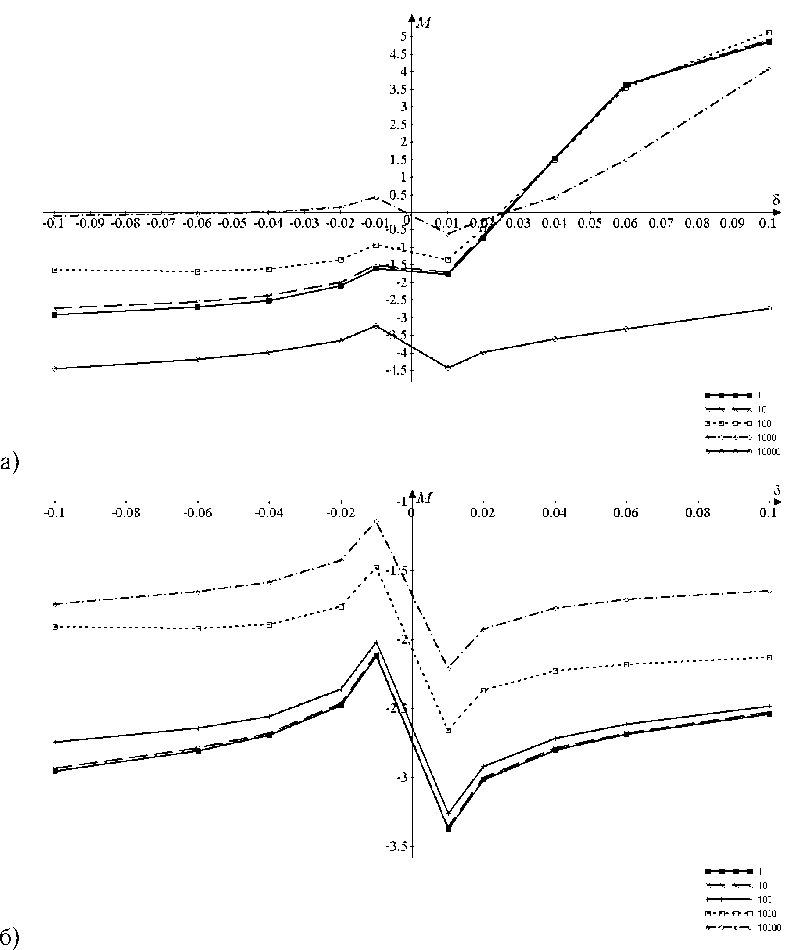
Рис. 5. Продольная компонента М тензора эластопроводимости проводящих 9 Zg GeNR как функция относительной деформации δ и концентрации дефектов атомов кремния ( а ) и олова ( б ) N _d = 1, 10, 100, 1000, 10 000

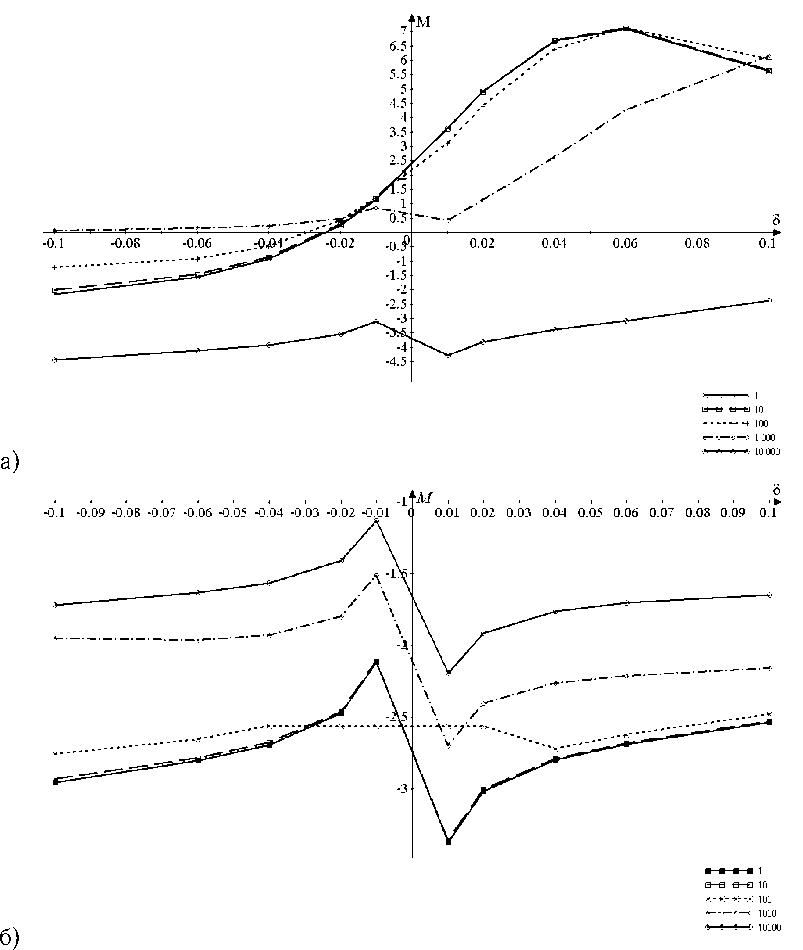
Рис. 6. Продольная компонента М тензора эластопроводимости проводящих 10 Zg GeNR как функция относительной деформации δ и концентрации дефектов атомов кремния ( а ) и олова ( б ) N = 1, 10, 100, 1000, 10 000

В случае с изоморфным дефектом олова описанного выше эффекта не наблюдается, поскольку уровень электрона на дефекте расположен относительно далеко от уровня Ферми.

Пьезорезистивность полупроводниковой германеновой наноленты структурной модификации типа «arm-chair» 10 Arm зависит от концентрации дефектов. Значения продольной компоненты тензора эластопроводимости М положительны практически во всем диапазоне δ, а тенденция ее изменения коррелирует с примесной концентрацией. Положительная величина М в области деформаций сжатия (5 < 0) означает, что проводимость наноленты уменьшается при деформации. Поскольку в полупроводниках проводи- мость обусловлена наличием запрещенной зоны шириной Ед, которая уменьшается при сжатии, то этот эффект связан с уменьшением плотности состояний. Тепловые флуктуации заполняют электронами зону проводимости NR согласно функции распределения Ферми — Дирака. Поэтому все меньшее число носителей заряда дает вклад в удельную проводимость кристаллита.

Таблица 1

Химический потенциал µ (мэВ) германеновых нанолент с изоморфным дефектом Si как функция относительной деформации 5 и концентрации дефектов N

9 Arm	N d
δ	1	10	100	1 000	10 000
-0,1	-423,31	-412,63	416,04	-466,74	-934,34
-0,06	-406,07	-406,3	-408,64	-440,59	-807,24
-0,04	-403,06	-403,25	-405,19	-430,93	-752,11
-0,02	-400,1	-400,26	-401,87	-422,77	-702,0
-0,01	-398,62	-398,77	-400,24	-419,1	-678,62
0	-397,38	-397,52	-398,86	-416,0	-657,75
0,01	-395,73	-395,85	-397,07	-412,51	-635,43
0,02	-394,3	-394,41	-395,52	-409,51	-615,48
0,04	-391,47	-391,56	-392,48	-403,98	-578,76
0,06	-388,65	-388,73	-389,49	-398,95	-546,22
0,1	-382,94	-382,99	-383,51	-389,99	-493,5
10 Arm	N d
δ	1	10	100	1 000	10 000
-0,1	-469,23	-436,72	-444,27	-503,44	-869,53
-0,06	-434,78	-416,94	-420,96	-462,75	-754,31
-0,04	-425,34	-410,76	-413,61	-446,7	-704,87
-0,02	-418,14	-405,82	-407,87	-433,42	-660,4
-0,01	-415,04	-403,63	-405,4	-427,75	-639,94
0	-401,71	-401,86	-403,4	-423,13	-621,7
0,01	-409,51	-399,62	-400,96	-418,07	-602,36
0,02	-406,87	-397,69	-398,87	-413,92	-585,16
0,04	-401,19	-393,57	-394,58	-406,63	-553,76
0,06	-394,13	-388,3	-389,35	-400,01	-526,05
0,1	-378,52	-375,08	-376,14	-386,04	-480,3

Положительное и практически монотонное поведение функции M (5) в области растяжения (5 > 0) связано с ростом удельной проводимости нанолент, что, в свою очередь, обусловлено конкуренцией двух эффектов. Это увеличение ширины запрещенной зоны с ростом деформации и увеличение плотности состояний в прифермиевской области энергий.

Разные типы дефектов (Si и Sn) в полупроводниковых нанолентах существенно влияют на качественное поведение функций M(5). В случае примеси кремния графики монотонно убывают. То есть в этом случае преобладает эффект увеличения Ед. Кривые для примеси олова монотонно возрастают, поскольку преобладает эффект увеличения плотности состояний. Проявление того или иного эффекта обусловлено различными уровнями электрона на дефекте е/ и удаленностью его от уровня химического потенциала. Следствием этого же является увеличение численного значения М с ростом концентрации атомов Si при фиксированной деформации в нанолентах. И, наоборот, уменьшение величины М с ростом концентрации атомов олова.

Таблица 2

Химический потенциал µ (мэВ) германеновых нанолент с изоморфным дефектом Sn как функция относительной деформации 5 и концентрации дефектов N

9 Arm	N d
δ	1	10	100	1 000	10 000
-0,1	-0,17	-1,69	-16,48	-135,42	-722,12
-0,06	-0,12	-1,18	-11,59	-99,7	-571,63
-0,04	-0,1	-0,99	-9,71	-85,19	-506,85
-0,02	-0,08	-0,82	-8,13	-72,6	-448,31
-0,01	-0,08	-0,75	-7,43	-66,9	-421,21
0	-0,07	-0,69	-6,86	-62,24	-398,08
0,01	-0,06	-0,63	-6,22	-56,85	-371,08
0,02	-0,06	-0,57	-5,69	-52,35	-347,94
0,04	-0,05	-0,48	-4,76	-44,31	-305,23
0,06	-0,04	-0,4	-3,98	-37,44	-266,98
0,1	-0,03	-0,28	-2,78	-26,6	-202,38
10 Arm	N d
δ	1	10	100	1 000	10 000
-0,1	-22,01	-23,03	-36,22	-0,15782	-697,42
-0,06	-3,05	-4,47	-17,95	-0,11246	-550,58
-0,04	-1,03	-2,21	-13,38	-0,09435	-487,42
-0,02	-0,4	-1,33	-10,27	-0,0789	-430,37
-0,01	-0,27	-1,09	-9,07	-0,07208	-403,98
0	-0,2	-0,94	-8,16	-0,06647	-381,5
0,01	-0,14	-0,79	-7,17	-0,06006	-355,2
0,02	-0,11	-0,69	-6,4	-0,05479	-332,69
0,04	-0,07	-0,54	-5,14	-0,04556	-291,2
0,06	-0,05	-0,43	-4,16	-0,03786	-254,08
0,1	-0,03	-0,28	-2,77	-0,02613	-191,58

При увеличении ширины полупроводниковых GeNRs на примере 50 и 100 Arm наблюдается в целом такое же поведение функции M (5), что было описано выше. Отличием является уменьшение численного значения величины М по сравнению с узкой лентой 10 Arm. Здесь проявляется еще один эффект, связанный с тем, что величина запрещенной зоны Е _д обратно пропорциональна ширине ленты. Расчеты показывают, что уровень химического потенциала µ всех изученных GeNR монотонно возрастает с ростом относительной деформации δ. Деформационный пиннинг химпотенциала обусловлен изменением зонной структуры GeNR вследствие взаимодействия электронов проводимости с дефектами структуры (Андерсоновской локализации). Поэтому увеличение концентрации точечных дефектов уменьшает значение величины µ при фиксированной деформации.

Выводы

В результате проведенного теоретического исследования изучены пьезорезистивные свойства германеновых нанолент — поведение продольной компоненты тензора эласто-проводимости, основной характеристики пьезорезистивного эффекта. Проанализированы ее зависимости от двух конкурирующих факторов: относительной деформации растяжения и сжатия и концентрации и типов примесей. Показано качественное согласие поведения тензора эластопроводимости в зависимости от добавления в структуру германена двух вариантов изоморфных дефектов из той же группы, но разных периодов.

В результате можно сделать вывод о том, что более ярко выраженными пьезорезистивными свойствами обладает германен с примесью олова. Это объясняется высокой подвижностью электронов валентной оболочки данного элемента по сравнению с атомом германия, которая оказывается более восприимчивой к деформации структуры наноленты. В соответствии с этим фактором такой материал может быть более эффективно интегрирован как базовый элемент устройств полупроводниковой электроники по причине высокой восприимчивости его свойств к эффектам деформаций и концентрации дефектов структуры, что в свою очередь дает возможность эффективного управления такими характеристиками, как проводимость и пьезорезистивность даже в ходе работы прибора на основе германена.