Оценка температуры при резании инструментами с криволинейной режущей кромкой
Автор: Рыжкин Анатолий Андреевич, Моисеев Денис Витальевич
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Технические науки
Статья в выпуске: 3 (78) т.14, 2014 года.
Бесплатный доступ
Рассмотрена теоретическая модель расчёта температуры на рабочих поверхностях инструмента с фасонным профилем режущего лезвия. Получены аналитические зависимости для оценки температурного состояния передней поверхности резца (зуба фрезы) с эллиптическим профилем в нормальных сечениях. Теоретические расчётные зависимости учитывают влияние на температуру теплофизических констант материала инструмента и детали, условия теплообмена, а также характеристики деформаций срезаемого слоя, элементы режимов резания и геометрию инструмента (при точении и фрезеровании). Полученные численные результаты температур для инструмента из твёрдого сплава марки Т15К6 и быстрорежущей стали марки Р6М5 соответствуют экспериментальным данным и могут быть использованы для прогнозирования интенсивности износа и эксплуатационной стойкости фасонного инструмента, в т. ч. резцов, дисковых и червячных фрез.
Температура резания, тепловой поток, коэффициент укорочения (усадки) стружки, угол сдвига
Короткий адрес: https://sciup.org/14250087
IDR: 14250087 | УДК: 621.9 | DOI: 10.12737/5709
Текст научной статьи Оценка температуры при резании инструментами с криволинейной режущей кромкой
Введение. В современных условиях механическая обработка материалов выполняется на высокопроизводительном оборудовании, и эффективность процесса определяется стойкостью инструмента. Этот показатель связан с температурным режимом зоны резания и уровнем средней температуры на контакте. Последняя зависит от режимов резания, физико-механических свойств инструмента и заготовки, а также от геометрии инструмента. Поэтому оценка температурного состояния зоны резания актуальна и не раз находила своё отражение в работах [1-3]. Задача решалась в одномерной постановке на примере токарного резца с прямолинейным лезвием, но для инструмента с криволинейным лезвием. Данные по определению температур по рабочим поверхностям отсутствуют.
При образовании сложных фасонных поверхностей, в т. ч. при зубофрезеровании (как по методу копирования, так и по методу обкатки) инструмент или повторяет профиль впадины зуба, или спрофилирован так, чтобы при обкатке получался требуемый профиль зуба зубчатого колеса. Наиболее часто встречающиеся профили зубчатых колёс — эвольвентный, радиусный (зацепление Новикова), циклоидальный, эллиптический и др. Суть эллиптического зацепления состоит в том, что в торцевом сечении косозубого колеса профиль зуба описывается уравнением окружности, а в сечении, нормальном зубу, получается эллипс, большая полуось которого равна радиусу окружности в торцевом сечении [4]. Параметры профилей таких зубьев и необходимые данные по профилированию обкатного инструмента были получены ранее [5-7].
Особенности сечения среза инструментом с криволинейным лезвием. В процессе резания форма криволинейного профиля зуба инструмента оказывает существенное влияние на его геометрию и на все характеристики резания. Если речь идёт о криволинейном лезвии, не остаются постоянными угол в плане, а также передний и задний углы для каждой точки криволинейной режущей кромки. Известно [8], что для криволинейного лезвия инструмента в зависимости от расположения точки на профиле изменяется и форма среза: при увеличении в плане угла ср до 90° срез становится более тонким и широким [8].
Закономерности обработки червячными фрезами зубчатых колёс с эллиптическим профилем изучались на модели при фрезеровании однозубой фрезой и точении фасонным резцом, повторяющим профиль зуба фрезы.
* Работа выполнена при финансовой поддержке РФФИ (грант № 12-08-01328-13).
Рис. 1. Сечения среза при обработке криволинейного профиля [8]
Особенность геометрии эллиптического зуба [4] заключается в следующем. В точке 1 (рис. 2) сопряжения выпукло-вогнутого профиля эллипса х = а (а — меньшая полуось эллипса) задний угол равен нулю и возрастает по мере приближения по криволинейному лезвию к точке 2, когда х = 0. Это означает, что процесс резания на вершине х = 0 будет наиболее благоприятным, а по мере приближения к малой полуоси х = а процесс резания становится невозможен. Кроме того, толщина среза, измеренная по нормали к кривой профиля в каждой точке лезвия, также разная: а3_4 >а5_6
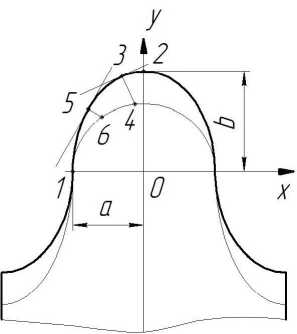
Рис. 2. Форма среза для эллиптического зуба
По этим причинам точно оценить теоретически тепловое состояние при резании криволинейным зубом, т. е. получить формулу для температуры резания, не представляется возможным. Поэтому в первом приближении следует использовать известные модели расчёта температуры для прямолинейных лезвий.
Теоретическая оценка температуры резания. Примем известную модель тепловой задачи трения [1] стружки о переднюю поверхность инструмента, полагая, что стружка в виде полубес-30
конечного стержня перемещается по неподвижному инструменту, который обменивается теплом с окружающей средой. Дифференциальное уравнение для стержня с граничными условиями имеет вид:
5^(х) Эх2
- mj^x) = О
8TyW _ (1-y0)Q
^ х=0 ^1
=()
Эх „
где q = q, • b ♦ +qTfl • y0; Аъ A2 — коэффициенты теплопроводности материала; 6* — доля теплово
го потока из зоны деформации в стружку; у0 — коэффициент ушедшего в стружку тепла трения по передней поверхности; (1 - XoYq — перешедшее в инструмент тепло от трения; а2 — коэффициент температуропроводности обрабатываемого материала; mi — коэффициент, учитывающий теплообмен инструмента с окружающей средой [1].
Определяя температуры Т^х.т) и Т^х) и приравнивая их значения при х= 0, находим коэффициент распределения тепловых потоков:
Vl3q8b*40Ja^
- у _ ЧуП ^Г 5^2Т
ПП "" ' ТП + ‘ ДП , /ГТ----
Х2 + Х^/л^ Wl, Ь^т
где Ттп — температура по передней поверхности от трения; Тдп — температура по передней поверхности от деформации сдвига; Тпп— суммарная температура по передней поверхности от трения и деформации сдвига; (7777 — тепловой поток от трения по передней поверхности.
Данное равенство выражает величину температуры на передней поверхности инструмента
в сечении, нормальном к режущему лезвию.
В свою очередь параметры, входящие в (3), находятся по формулам: q = X- • 0,252 • ст , И ПТ I/ ’— в *
qd
Ь* =
1 + 1,33.
28 • sin т =-------
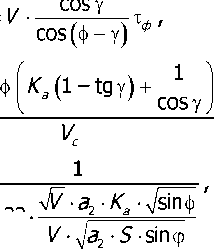
где Ка — коэффициент усадки стружки.
По полученным зависимостям производится расчёт температуры по передней поверхности инструмента с прямолинейным профилем. Чтобы перейти к модели, учитывающей тепловое состояние для криволинейного профиля, необходимо модернизировать полученные зависимости с поправкой на геометрию инструмента. Из полученных выражений видно, что формулы (5) — (7) — это функции q„ = /^(ф, у,ф), т = ^(ф, у, ф), Ь* = fз(ф, у, ф), зависящие от режущей геометрии инструмента в текущей точке (у — передний угол, ср — главный угол в плане, ф — угол сдвига). Таким образом, температура по передней поверхности инструмента при точении фасонным резцом с криволинейным профилем есть функция от входящих в неё геометрических параметров:
Тпп = ТпМ 1, ф) + Тдп (ф, Y, ф) ■
Для расчёта температуры определим параметры ср, у, ф, представив их как функции, зависящие от координаты: ф(х), у(х), ф (х) (рис. 3), т. е. возьмём бесконечное число сечений Дбм-
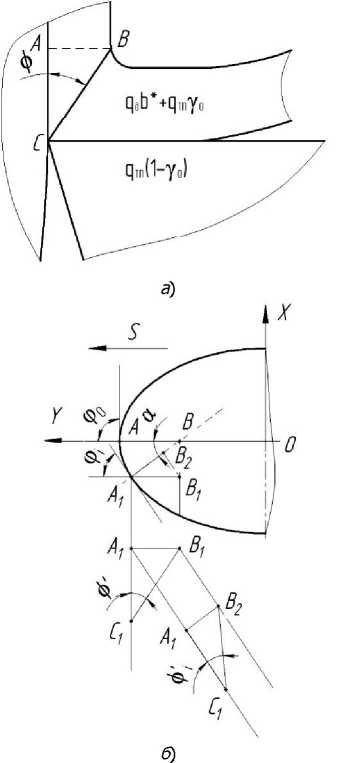
Рис. 3. Обработка криволинейным лезвием. Схема схода стружки (а); расчёта угла сдвига (б)
При расчёте необходимых параметров будем использовать уравнение эллипса:
— + 2_ = 1.
а2 Ь1
Определим параметр ф'(х). Из рис. 3 видно, что угол сдвига в нормальном сечении равен:
А,В7 И
1дф; = ^yKv = j^-COSa-^ =1дф-СО5а-К1/, где ф — угол сдвига в сечении по оси OY; Kv = ——— — коэффициент, учитывающий разную скорость резания по длине режущего лезвия; D— диаметр обработки.
Таким образом, в общем виде получим:
, . D + Ad )
ср' = arctg tgcp———cos а .
В полученном выражении неизвестным остаётся параметр а. Для его определения вое пользуемся схемой (рис. 4).
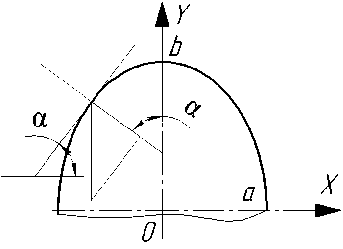
Рис. 4. Профиль эллиптического фасонного резца
Так как уравнение кривой эллипса при
X2 у>0 f(x) = b.l-^, a cos« = V а
= =, получим зависимость угла сдвига ф'
Vl + f'W от абсциссы х.
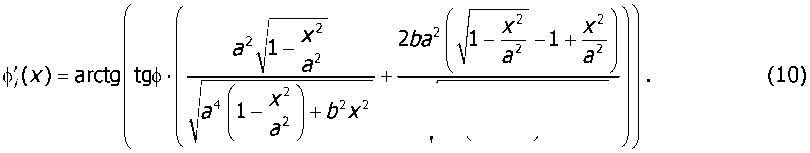
Определим параметр ф(х). Главный угол в плане как функция координаты х определяется с помощью производной функции, описывающей криволинейный профиль инструмента (рис. 3):
|
D |
a4 l-^ +^x2 |
|
1 а ) |
(И) Определим текущий передний угол у(х). В нашем случае он постоянен и равен нулю YW = 0. Учитывая зависимости (10) — (11) и (3) — (7), получим систему выражений, необходимых для расчёта температуры по передней поверхности инструмента:
ТПМ
Ф, у) =
Qtt?^Фа у) •
^,5аг^,
ф, у)
Ъ13(79(ф,
ф, у) •
b
* (ф, ф, у) • уоЛ/^(фГфл) Х2 + /^m^l, S^t^P, ф, у)
т (ф, Ф, у) = b * (ф, Ф, у) =
I/ •
^аг
• S 51пф
С учётом геометрических особенностей эллиптического профиля зуба:
у(х) =
0.
фн) = 2
- f (%)=yarctg
5 Л1--г
V
а
На основании полученных зависимостей (12) — (13) был произведён расчёт температур по передней поверхности инструмента для разных пар материалов инструмент — деталь: Т15К6 — сталь 45 (рис. 5, а), Р6М5 — сталь 45 (рис. 5, б). Рис. 5. Распределение температур по передней поверхности эллиптического фасонного резца для пар: Т15К6 — сталь 45 (а); Р6М5 — сталь 45 (б) Исходные данные (рис. 5):
режимы резания:
5=
0,14 мм/об;
D =
0,1 м;
t=
0,5ЛО-3 м; параметры эллипса:
а
= 4,5‘10-3 м;
b
= 5‘10-3 м;
— сталь 45: oB = 598 МПа;
3i
= 8-10”6 м2/с; A2 = 40,1 Вт/мтрад; cpi = 5,02"106 Дж/м3трад;
— T15K6:
3i
= IO-5
m2/c;
Ai = 27,2 Вт/мтрад; cpi = 2,72"106 Дж/м3трад;
mi
= 40
m-1;
— P6M5;
3i
= 4,3’Ю-6 м2/с; Ai = 20,4 Вт/мтрад; cpi = 4,77"106Дж/м3трад;
mi
= 46
m”1.
Из рис. 2 и 5 видно, что максимальная температура по передней поверхности резца соответствует максимальной ширине среза (х = 0). По мере приближения к периферийному участку лезвия (х = а) температура, как и ширина среза, стремится к нулю.
Заключение.
Предложенная модель позволяет получить аналитические зависимости для расчёта температуры по передней поверхности инструмента криволинейного профиля по длине его лезвия.
Полученные данные позволяют прогнозировать наибольший износ задней поверхности на участке, где температура максимальна, и оценить стойкость инструмента с криволинейным (эллиптическим) профилем режущей кромки.
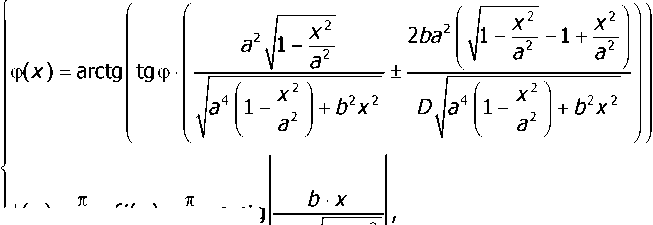
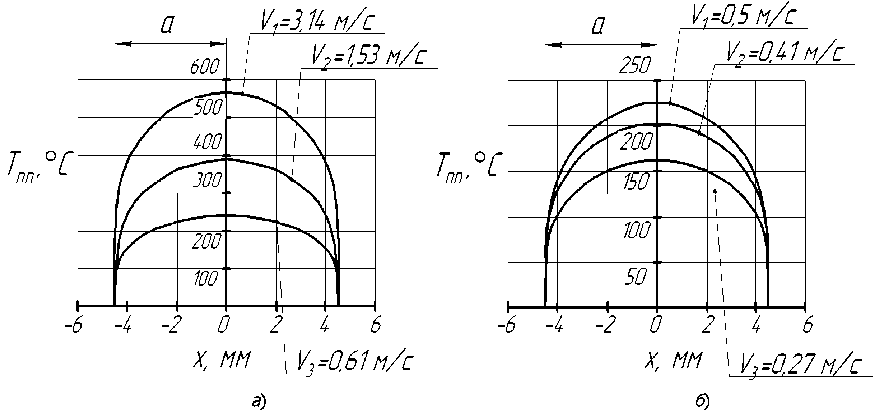
Список литературы Оценка температуры при резании инструментами с криволинейной режущей кромкой
- Рыжкин, А. А. Обработка материалов резанием: физические основы/А. А. Рыжкин. -Ростов-на-Дону: Изд. центр Дон. гос. техн. ун-та, 1995. -242 с.
- Висторопская, Ф. А. К вопросу о коэффициенте распределения теплового потока в зоне деформации при резании/Ф. А. Висторопская, А. А. Рыжкин, С. А. Моисеенко//Вестн. Дон. гос. техн. ун-та. -2012. -№ 6 (67). -С. 41-46.
- Расчёт температуры задней поверхности режущего инструмента/А. А. Рыжкин [и др.]//Проблемы синергетики в трибологии, трибоэлектрохимии, материаловедении и мехатронике: сб. тр. XI Междунар. науч.-практ. конф. -Южнорос. гос. техн. ун-т. -Новочеркасск, 2012. -С. 4-21.
- Зубчатая передача: патент 2057267 Рос. Федерация: F16H1/24/Г. П. Гребенюк. -Заявл. 07.04.93; опубл. 27.03.96, Бюл. № 9. -5 с.
- Определение координат боковых сторон зубьев колёс с эллиптическим профилем/А. А. Рыжкин [и др.]//Вестн. Дон. гос. техн. ун-та. -2009. -Т. 9, № 2 (41). -С. 284-295.
- Рыжкин, А. А. К вопросу аналитической оценки профиля эллиптического зуба колеса/А. А. Рыжкин, Д. В. Моисеев//Вестн. Дон. гос. техн. ун-та. -2009. -Т. 9, № 4 (43). -С. 698-710.
- Определение профиля червячной фрезы для изготовления зубчатых колёс эллиптического профиля/А. А. Рыжкин [и др.]//Вестн. Дон. гос. техн. ун-та. -2010. -Т. 10, № 5 (48). -C. 731-743.
- Ящерицын, П. И. Теория резания/П. И. Ящерицын, Е. Э. Фельдштейн, М. А. Корниевич. -Минск: Новое знание, 2006. -512 с.


