Оценка тенденций изменения человеческого капитала социально-экономической системы на основе применения алгоритма нейросетевого прогнозирования

Построение стратегии развития социальноэкономической системы, в которую закладывается стабильный рост ее показателей, является актуальной задачей. При ее решении должен быть использован аппарат математического моделирования, поскольку он позволяет с заданной точностью строить экономические зависимости на будущее.

Стратегия развития социально-экономической системы предполагает построение схем финансирования производственной и социальной сфер деятельности. Производственная сфера характеризуется структурой и величиной производственного капитала (ПК), методология расчета которого хорошо известна. Для оценки социальной сферы в последнее время все чаще применяется такой показатель, как человеческий капитал (ЧК), в условиях современной экономики являющийся ведущим фактором, определяющим высокие темпы развития. Следовательно, вопросы, связанные с изучением человеческого капитала, становятся важными и актуальными.

Понятие ЧК появилось в науке в XX веке в работах американских ученых-экономистов Дж. Минсера [1], Т. Шульца [2] и Г. Беккера [3]. Толчком к созданию теории ЧК послужили статистические данные, касающиеся роста экономик развитых стран мира. Анализ реальных процессов развития и роста в современных условиях привел к изучению ЧК как основного производительного и социального фактора раз- вития. За создание основ теории человеческого капитала были присуждены Нобелевские премии по экономике (Т. Шульц, 1979 г. и Г. Беккер, 1992 г.). Существенный вклад в формирование теории ЧК внес С. Кузнец. Он показал, что ЧК выступает главной доминантой возможного стабильного роста экономик развивающихся стран [4].

К числу ученых, внесших наибольший вклад в развитие теории человеческого капитала, относятся М. Блауг, М. Гроссман, М. Перлмен, Л. Туроу, Ф. Уэлч, Б. Чизуик, Дж. Кендрик, Р. Солоу, Р. Лукас, Ц. Грилихес, И. Фишер, Э. Денисон и другие экономисты, социологи и историки. Среди современных отечественных исследователей, занимающихся проблемами ЧК, можно отметить С.А. Дятлова, Р.И. Капелюш-никова, М.М. Критского, С.А. Курганского, О.И. Иванова и других. Существует несколько подходов к оценке человеческого капитала. Известны модели И. Бен-Порэта [5], Д. Хекмана [6], А.С. Акопяна, В.В. Бушуева и В.С. Голубева [7], С.Ю. Малкова, К.А. Болоховой и О.И. Давыдовой [8].

Построение общей методики расчета ЧК является достаточно трудной задачей, поскольку существует большая доля субъективных оценок при его моделировании. Различаются и позиции, на основе которых формулируется понятие ЧК, в частности, он может быть изучен с точки зрения качества жизни человека [9], его способности к высокопроизводительной деятельности [10], как объем доходов, которые способен получить человек [11] или как объем инвестиций в социальную сферу [12]. В рамках Программы развития ООН в 1990 году предложена методика оценки уровня ЧК, основанная на расчете индекса человеческого развития1.

Какой бы подход ни был выбран исследователем для оценки ЧК, важно, что в настоящее время этот показатель следует рассматривать в качестве одного из наиболее важных факторов, обеспечивающих развитие социально-экономической системы [13–17].

В нашей работе использовалась интегральная экономико-математическая модель ЧК, включающая в себя его количественные и качественные характеристики [18]. На основе этой модели производился расчет величины ЧК. Прогноз ЧК осуществлялся с применением нейросетевого алгоритма.

Нейросетевое моделирование выступает одним из математических методов исследования различного рода процессов и явлений, применяется для решения задач интеллектуального анализа и прогнозирования данных [19–22].

Изначально искусственные нейронные сети (ИНС) были сконструированы в результате изучения нервной системы живого организма [23]. Нейронная сеть является в определенном смысле аналогом мозга по качественной структуре и количеству нейронов, содержащихся в ней.

В последние десятилетия нейронные сети широко используются для прогнозирования. Прогнозирование представляет собой одну из самых востребованных, но при этом самых сложных задач интеллектуального анализа данных. Погрешность прогноза всегда зависит от выбранной модели, наличия и качества исходных данных.

Нейронные сети обладают следующими преимуществами при построении прогнозов: результативность при решении неформализованных или плохо формализованных задач; устойчивость к частым изменениям среды; эффективность при работе с большим объемом противоречивой или неполной информации. Эти преимущества актуальны, в том числе, и при применении нейронных сетей к прогнози- рованию социально-экономических процессов и явлений.

Преимущества, связанные с использованием нейросетевых моделей и их модификаций при анализе социально-экономических процессов и явлений, представлены в работах [24; 25]. Показано, что нейросетевые модели обладают свойством учитывать влияние неявных факторов и включать в исследование неочевидные математические связи, которые сложно найти с помощью классических эконометрических моделей, в частности регрессионных.

Впервые об ИНС заговорили в 40-х гг. XX века. Считается, что в качестве научного направления теория нейронных сетей была обозначена в 1943 году в работе У. Мак-Каллока и В. Питтса [26], где было показано, что любую арифметическую или логическую функцию можно реализовать с помощью простой нейронной сети. Среди основополагающих работ также следует выделить модель Д. Хэбба [27], который в 1949 году предложил первый алгоритм обучения. В 1958 году Ф. Розенблатт сконструировал модель перцептрона, содержащего один слой [28]. После некоторого охлаждения к ИНС в 70-х гг. возникла новая волна интереса. Благодаря исследованиям Т. Кохоне-на, С. Гроссберга и Д. Андерсона был достроен фундамент, на основе которого стали возможны построение и использование многослойных нейронных сетей [29; 30]. В 1974 году П. Вер-бос для обучения многослойных нейронных сетей разработал базовый алгоритм, который нашел широкое применение на практике [31]. Среди исследователей в области ИНС можно выделить также М. Минского [32], К. Фукусиму [33], Дж. Хопфилда [34], С. Хайкина [35], Р. Хехт-Нильсена [36] и др. Исследования последних лет по формированию алгоритмов нейросетевого моделирования, анализа динамических рядов, прогнозирования представлены, например, в работах [37–40].

Мы рассматриваем задачу прогнозирования человеческого капитала социально-экономической системы на основе нейросетевого алгоритма. Структура исследования представлена на рисунке 1 . Индикаторы направлений социально-экономического развития определены в соответствии с работой [41]. Алгоритм нейросетевого моделирования и прогнозирования составляющих ЧК позволяет осуществить

Рис. 1. Структура исследования

Индикаторы основных направлений социальноэкономического развития

Алгоритм нейросетевого моделирования и прогнозирования составляющих человеческого капитала

РезультатыI решения задачиI прогнозированияI качественных составляющих человеческого капитала

РезультатыI решения задачиI прогнозированияI количественных составляющих человеческого капитала

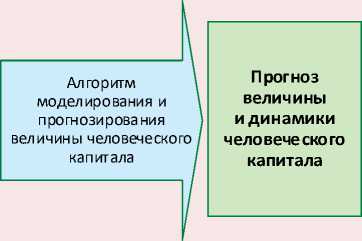
Источник: разработано авторами.

их прогноз. В алгоритме моделирования и прогнозирования величины ЧК используются результаты прогнозирования составляющих ЧК для расчета его суммарной величины.

Экономико-математическая модель человеческого капитала

Носителями человеческого капитала являются демографические элементы, каждый из которых в момент времени t характеризуется возрастом τ. Численность демографических элементов определяет количественную характеристику ЧК. Для реализации эффективной демографической политики большое значение имеет проведение таких исследований, как анализ современных демографических процессов и прогнозирование на его основе численности и структуры населения, учитывающее специфику рождаемости, продолжительности жизни, миграционных процессов, смертности.

На рисунке 2 на примере одного из регионов РФ – Удмуртской Республики (УР) – приведена динамика общей численности населения за период 1997–2018 гг., на рисунке 3 – динамика рождаемости и смертности.

Рис. 2. Динамика численности населения УР

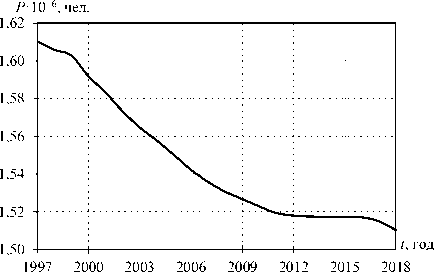
Источник: Общая численность населения Удмуртской Республики. URL:

Рис. 3. Динамика рождаемости (1) и смертности (2) населения УР

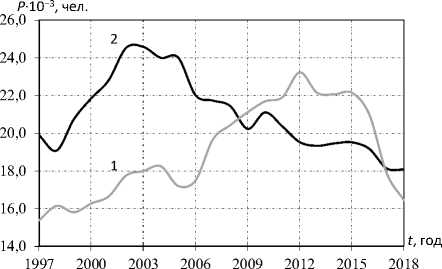
Источник: Население Удмуртской Республики по полу и возрасту. URL:

Рис. 4. Плотность распределения населения УР по возрастам: 2008 г. (1); 2018 г. (2)

ρ·10-3, чел.

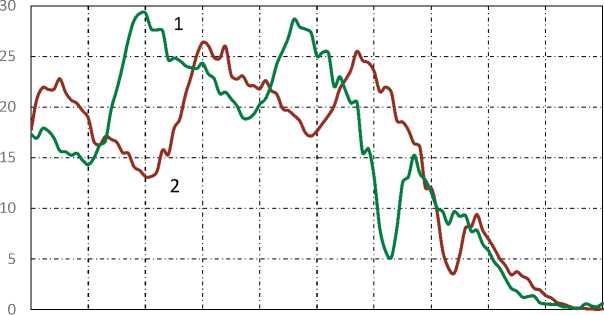
0      10     20     30     40     50     60     70     80     90    100 τ, лет

Источник: Естественное движение населения Удмуртской Республики. URL:

Расчет величины ЧК необходимо проводить с учетом демографической структуры. Важное значение в данном случае имеет распределение демографических элементов по возрастам ρ ( t , τ ). Под демографическим элементом здесь и далее будем понимать представителя народонаселения – отдельного человека, который в рассматриваемый момент времени t характеризуется возрастом τ . На рисунке 4 представлена плотность распределения населения УР по возрастам для 2008 и 2018 г. соответственно. Функция ε ( t , τ ) задает долю населения возраста τ , участвующего в общественном производстве в год t . Задача моделирования и прогнозирования демографической динамики подробно представлена в работе [42].

Для расчета величины человеческого капитала экономической системы Н(t) используется модель [18], в соответствии с которой суммарная величина ЧК населения, участвующего в общественном производстве, определяется с помощью выражения:

H ( t )=№ ah i ( t,T ) e ( t,T ) p ( t,T ) dT . (1) 0 i = ¹

Функции hi(t,τ) являются качественными составляющими ЧК: здоровье i=1, образование i=2, культура i=3. Капиталовложения в здраво- охранение повышают общий уровень здоровья в обществе, что способствует, с одной стороны, продлению экономически активной жизни отдельного демографического элемента, с другой стороны, увеличению количества экономически активных демографических элементов вследствие снижения уровня смертности. Инвестиции в образование способствуют повышению общего уровня квалификации на региональном рынке труда, открывая наибольшие резервы для роста эффективности функционирования современной экономики. Вложения в культуру улучшают среду обитания человека, формируют нравственные ценности, повышают творческий потенциал личности, что, безусловно, сказывается на социально-экономическом развитии региона.

Удельное (на одну демографическую единицу) среднестатистическое значение ЧК определяется линейной комбинацией:

h (t, t) = a 1 h 1 (t, t) + a₂ h ₂(t, t) + a₃ h ₃(t, t), (2)

« i ^e(o,i); E a =^{1, (3)} i =1

где α_i – соответствующие весовые коэффициенты для составляющих ЧК; значения h_i ( t,τ ) измеряются в денежных единицах.

При проведении исследования была принята гипотеза о равнозначности компонент ЧК: Ф = 1/3, i = 13.

Эволюция каждой из составляющих ЧК описывается уравнением:

д h j(t, t) д h (Л, t)

—dt— + —дт— = -^ h j ⁽t, т) + ^st ⁽t, т) + Pt (t, т) .(4)

В формуле (4) используются следующие обозначения для каждой i -ой составляющей ЧК: s_i = s_i ( t,τ ) – удельные расходы государства ( state – англ. «государственные»); p_i = p_i ( t,τ ) – удельные частные инвестиции ( private – англ. «частные»); v_i = v_i ( t,τ ) – коэффициент выбытия, который оценивается с помощью алгоритма идентификации [43].

Начальные условия при t = t ₀ имеют вид:

hi (to, 1) = hй(т), (i = 1,2,3), где hi0(t) – известные функции.

На левом конце демографической кривой граничные условия имеют вид:

ht (t,0) = 0, (i = 1,2,3);(6)

V

на правом конце при i = 1, 2 следует записать:

ht(t, да) « ht(t, Tm) = 0,(7)

где τ_m = τ_m(t) – время дожития δ процентов населения ( δ = 1–5% ) .

Очевидно, что коэффициенты выбытия v_i слабо зависят от времени. Зависимость от возраста для функций v_i = v_i(τ) (i = 1, 2 ) примем в виде:

^(t) =

⁰ , ^T<^T ai,                                                          ,

^{( S}i ⁽ t , ^{t) +} P. ^{( t} , ^Т)М^еХР[б , ^(t - ^T ai ^)]- 1} , ^T ai < ^T< ^T m ,

где неизвестные параметры ( s_i , ε_i ) определятся из условий:

( 5 i (t , т ) + p i ( t , т)){ехр [ e i ( t m - т ai ^)] -^1} = 1    ⁽⁹⁾

j[ s , ( t , t ) + p i ( t , t )] d t =

= J^{{( s} i ^{( t} , ^{t) +} p ^ t ,^т))(ехр^[е , .^(т-т „, )]-1)} h i ^{( t} , ^t) d ^t ()

Здесь τ_ai – верхняя граница активного периода физического состояния ( i =1) или трудовой деятельности ( i =2).

При проведении конкретных расчетов для экономической системы УР были проанализированы демографические данные за 2000– 2018 гг. Установлено, что возрастные ограниче- ния экономически активного возраста населения УР – 20–60 лет.

В отличие от других составляющих культурная составляющая ЧК не подвержена выбытию, поэтому v ₃ ≡ 0.

Для задающего эволюцию составляющих ЧК уравнения (4) распределение по возрастам удельных составляющих бюджетных расходов государства s_i (t,τ) определим по формулам:

S i ( t . r )=X t;;^- .

^№f p ( t . T ) d T

T ;,                       (11)

J ^S _N i ⁽ t ^,T ) . ^T e [ ^T₁ ; . ^T ; ; ^].

^SNi ⁽ t )    ]

1° . ^T ^V ^T 1 Ni . ^T 2 ; J-

Здесь SNi (t) – суммы, закладываемые в бюджете на соответствующую статью расходов Ni (Ni – нумерация статей бюджета, расходуемых на здравоохранение (i=1), образование (i=2) и развитие культурной составляющей ЧК (i=3)). В соответствии с формулой (11) эти суммы будем распределять равномерно на соответствующие периоды жизни человека [τ1Ni, τ2Ni] и на количество демографических единиц в этих пе- риодах.

Для уравнения (4) распределение по возрастам удельных составляющих частных расходов p_i ( t, τ ), направленных на приращение ЧК, запишем по аналогии с (11) в предположении, что в разные периоды жизни человек использует разные денежные суммы, расходуемые на здравоохранение ( i =1), образование ( i =2) и культуру ( i =3):

Pi(t,r )=Z T-P^t-, i И,T)dr           (12)

J Pi ( t^,T ), т е^[г n,T ₂ i ],

Pi ^{( t} ) I A Г "I

I^{0, T} ^^{[ T} 1 i^,T 2 i J-

Алгоритм нейросетевого прогнозирования человеческого капитала

Построим нейронную сеть для решения задачи прогнозирования человеческого капитала. На рисунке 5 представлен элемент нейронной сети – нейрон, у которого имеется m входов и выход. Такая конструкция нейрона называется персептрон. Искусственная нейросеть – это способ собрать нейроны в сеть для решения определенных задач. Обученный искусственный нейрон работает следующим образом: каждый вход умножается на некие веса; далее все суммируется и прогоняется через нелинейную активационную функцию, а результат подается на выход. Все нейроны собираются по слоям. Основные вычислительные операции выполняются на внутренних скрытых слоях.

Другая задача – обучить нейрон. Обучение заключается в том, чтобы найти правильную весовую информацию, которая корректируется, исходя из поставленной задачи и ошибки (разности между вычисленными и идеальными выходными значениями). Для этого используется алгоритм обратного распространения ошибки.

Входные данные суммируются с весовыми коэффициентами w.: D - £ wjxj. На выходе ней-j            j-i рона присутствует логистическая активационная функция f(D) (см. рис. 5), которая преобразует взвешенную сумму D входящего сигнала (рис. 6).

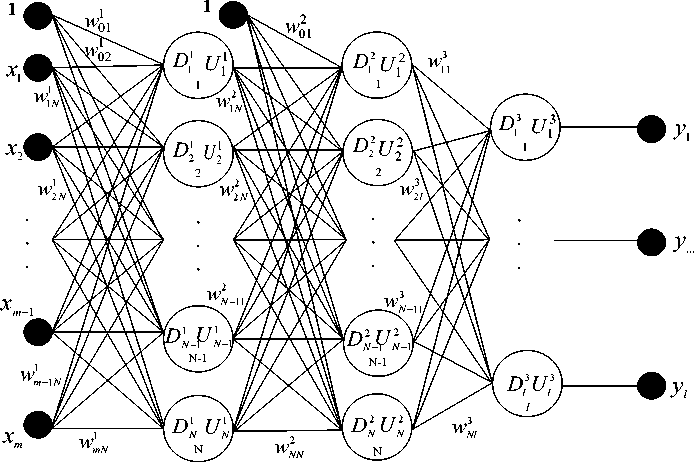
Для прогноза объемов инвестиций в социальную сферу сконструируем сложную k -слойную нейронную сеть с m входами и l выходами (рис. 7) . Входными данными в нейросетевой модели являются объемы

Рис. 5. Искусственный нейрон                        Рис. 6. Активационная функция

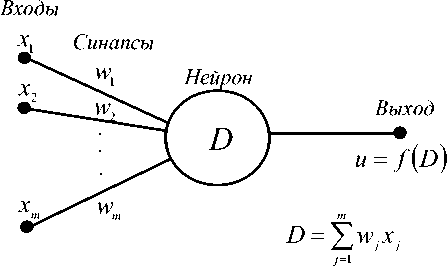
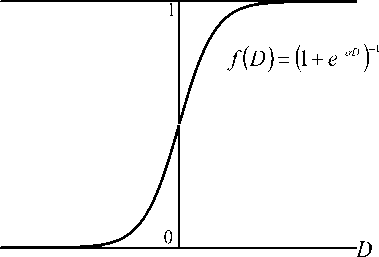
Рис. 7. Нейросетевая модель, используемая для прогнозирования инвестиций в человеческий капитал

Источник: разработано авторами.

бюджетных { S i } n = и частных инвестиций { P i } " =3 в ЧК, показатели-индикаторы направлений социально-экономического развития { I i } n^ . Для учета инфляционных процессов используется индекс-дефлятор K . Выходные данные нейронной сети – это прогнозные ежемесячные объемы бюджетных и частных инвестиций в ЧК: n =3           n =3

^{ ~ L и ^{ P ^}=1 .

Для нашей задачи на входе будем рассматривать бюджетные инвестиции в здравоохранение ( x ₁ ), образование ( x ₂ ), культуру ( x ₃ ), а также частные инвестиции в здравоохранение ( x ₄ ), образование ( x ₅ ) и культуру ( x ₆ ). Объемы инвестирования в социальную сферу зависят от множества факторов и окружающих условий. В работе С.А. Айвазяна [41] были выявлены показатели, наиболее сильно влияющие на качество социальной сферы, а именно: валовой региональный продукт ( x ₇ ), среднедушевые денежные доходы ( x ₈ ), производство товаров и услуг на душу населения ( x ₉ ), площадь введенного жилья ( x ₁₀ ), количество зарегистрированных преступлений ( x ₁₁ ), естественный прирост населения ( x ₁₂ ), смертность в трудоспособном возрасте ( x ₁₃ ), минимально необходимый месячный доход ( x ₁₄ ).

Таким образом, { 5 , }"3 = { x ,, x 2, x 3}, ^{ P, ^} " ^ = ^{ x 4, x 5, x 6^}, { I . } M = ^{ x 7, x 8, x 9, x 10, x 11, x 12, ^X 13, x 14 ^} , K = X 15 .

Алгоритм нейросетевого прогнозирования построим для произвольного случая с любым количеством входных переменных. На рисунке 7 представлена нейросетевая модель, положенная в основу алгоритма.

В каждом слое нейросетевой модели содержится N_p нейронов, p =1,…, k .

Будем использовать следующие обозначения: W q — весовой коэффициент связи, соединяющий сигнал, выходящий из ( p- 1)-го слоя i -го нейрона и входящий в j -й нейрон p -го слоя. Для каждого слоя коэффициенты представим в виде матрицы размером ( N_p -1 + 1)х N_p :

W = ( wp ), p = 1,.., k ; i = 0,.., N , -,; j = 1,.., N , . (13)

С алгоритмической точки зрения выходные значения нулевого слоя u 0j следует приравнять к входящим в нейронную сеть сигналам xj, x0 ≡ 1

u 0 = x j , j = 0,.., m .

В остальных слоях выходные значения нейронов вычисляются:

uP = 1, u^p = f ( dj ) p = 1,.., k , j = 1,.., Np,   (15)

где f ( d j ) — нелинейная активационная функция вида f ( t ) = (1 + e~™ )^-1 , a — некоторый коэффициент.

Обозначим через d _j ^p входящий сигнал в j -й нейрон p -го слоя, который определяется взвешенной суммой входящих в него сигналов:

N p -1

d p = £ w p u p , ^j = ^1,.^, N p .          ⁽¹⁶⁾

i =0

Выходные значения последнего k -го слоя должны соответствовать y_j :

yj = uk^k , j = 1,.., l ,                (17)

Процесс обучения состоит в подстройке весовых коэффициентов w _i ^p _j . На основе информации о значениях переменных в известные моменты времени сеть определяет их наиболее вероятные значения на будущее. Статистическая информация по социально-экономическим показателям делится на два множества: обучающее и тестовое, представляющее из себя участок ретропрогноза.

Для обучения сети на входы подают входные данные x _q = ( x_{q 1} , x_{q 2} ,…, x_qm ) и сравнивают выходные значения сети с идеальными (реально заданными) значениями r _q = ( r_{q 1} , r_{q 2} ,…, r_ql ), q =1,…, n .

На обучающем множестве данных реализуется алгоритм обучения многослойной нейронной сети методом обратного распространения ошибок, который относится к градиентным методам оптимизации [44]. Для определения весовых коэффициентов VW = (wp ) сети используется погрешность обучения сети, рассчитанная по формуле:

E q (1W )= 1 1 ( y j - j , q =^1,.., n ,     (18)

2 j =1

где y_qj соответствует j -му выходу при подаче на вход q -го образа.

При подаче q -го наблюдения коэффициенты будут изменяться так:

W 2 ( q )= W ( q -1)+ (-X-V E p ) , (19)

где W ( q ) — состояние вектора W после обучения сети по q -му наблюдению; X е (0;1] — скорость обучения сети; ∇ E_q – градиент функции Eq (VW ) , когда на вход подается q -й образ:

f^ Eq . )

Vw j

V ^Eq

J = 1,..., Np . (20)

В компонентной форме выражение (20) представим в виде:

r qi

r qi

—

v im¹

max min ф .   ^— ф .

q = 1,

, n .

wp ( 1 ) = wp ( 1 -1 ) + A wp , A wp =-X     . (21)

Swj

Компоненты вектора (21) распишем следующим образом:

Чтобы получить реальные значения выходных данных, необходимо сделать обратное преобразование:

y q, =Ф mn + У q, (ф Tax "Ф Tn ) , 9 = 1,..., П ,    (31)

d E

q

d E q d u^p d d j

a w p   a u p a d j a w p ,

∂u p где частную производную j , в соответствии с производной логистическj ой функции

где y_qi – реальное значение функции; ^y qi – i -ое выходное нормированное значение функции при поданном на вход сети q -м образе.

ft ) = a f ( t )( 1 - f ( t )) представим в виде:

a up

—- = а • u ' • ( 1 - u p ) .

ddp        j V 11

Качество обучения сети определяется погрешностью обучения по формуле:

E ( W ^ )= 100 -^ in^ E q ( W ) .       (32)

\ l • П q =1

Погрешность расчетов определяется по

Введем новую переменную δ ^p _j следующим образом:

формуле:

8 ^p = ^j

d E q d u⁷

HW dd7 ’ jj

~=₂ p

My y e [ 2000,2018 ]     y

,

d E q = ^i d E q d u^{p +1} d d^{p +1}

dup    и dup+1 ddp+1 dup jiij

= N g d E q a u p ⁺¹

i =1

a u p ⁺¹ ad^{p +1} l                       I

W ⁺1 . (25)

Тогда δ ^p _j можно рекурсивно вычислять через данные (p +1)-го слоя 5 p ⁺¹ :

где M_y – количество заданных точек показателя y на оси времени; y ^* – значения, полученные по модели; y – реальные статистические данные.

⁵ pp =

Np +1

h 5 Г *¹ wp *1

i =1

• a • u ' • (1

—

u p ) . (26)

При p = k из формул (16), (23) и (24), приравнивая u/ = y_qj , находим:

8f = [uf - r_qj\ • a -uf • (1 - u^) .   (27)

Последний множитель в формуле (22), ∂d p согласно (16), равен: ∂dj =up-1 .

^{∂ w} ij ^{p i}

В результате на основании формул (21), (22), (24) получаем разностную схему:

j- 1 q )= j- ( q - i)-^s j U ' p ^-1 .         (28)

Для того чтобы обучить сеть, необходимо

нормировать входные и выходные данные в области их определения. Если известно, что x_j ∈ [ a_j – h_j ; b_j + h_j ], то нормированные входные данные имеют вид:

x = x q, ^{-( b}J ⁺ a J )^{1 qj   ( b}J ^- a J ) ¹ + ^hJ ’

q = 1,

n .

Если известно, что изменение i -ой выходной функции находится в пределах [ф min, ф max] , то нормированные выходные данные имеют вид:

Результаты нейросетевого прогнозирования человеческого капитала

Проведем расчеты человеческого капитала на примере социально-экономической системы Удмуртской Республики (УР). В построенной нейросетевой модели количество входных ⁿ =3 ⁿ=V¹ =3          n =8

нейронов N =16 (1,{ S j _{i =1}, { P_t } _{j =1} , { L} = _x , K ) , количество скрытых слоев равно двум (см. рис. 7). Статистические данные по этим показателям для УР представлены в таблицах 1, 2.

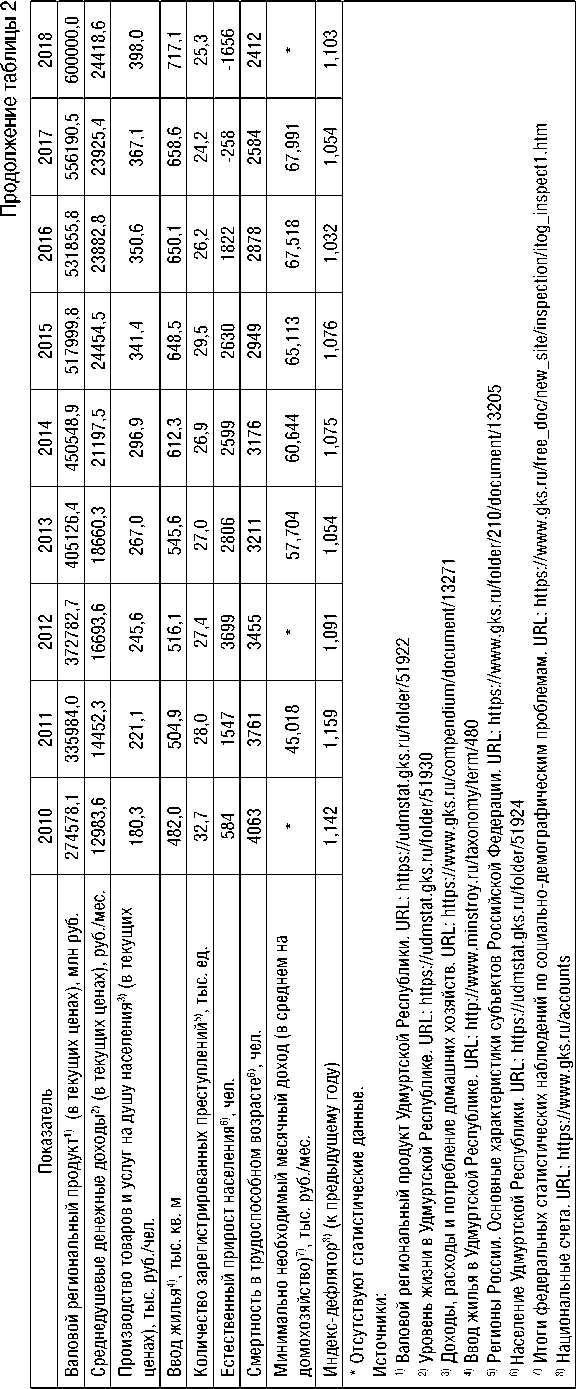
В таблице 1 отражены годовые бюджетные и частные инвестиции, направленные на развитие человеческого капитала УР, за период 2000–2018 гг. по информации Федерального казначейства РФ, Территориального органа Управления Федерального казначейства по Удмуртской Республике и Федеральной службы государственной статистики РФ.

Динамика индикаторов направлений социально-экономического развития УР по данным Федеральной службы государственной статистики, Территориального органа государственной статистики по УР, а также федеральных статистических наблюдений по социально-демографическим проблемам показана в таблице 2.

Таблица 1. Бюджетные и частные инвестиции, направленные на развитие человеческого капитала УР, за 2000–2018 гг., в текущих ценах, млн руб.

g

s

О GE О e x X 1™ о * El 2 \o CD X 03 X X X CD 03 1— о Q-ГО d & о X X c: ro 3 Q-O I— 3 Q-Q-O I— 3 CL > ГО 1™ О * GE 2 \o о о X го 03 о Q-3 GE 3 d О о X о й о X о го О-

СМ со со

от

О

8

а> со со со см

g"

от

CD.

го"

1

g"

CD_

eT о см

cd"

от"

о>"

го

CM со CM

Q-> О GE О e X X 1™ о * GE 2 ra CD X 03 X X X о 03 о Q- ГО GE О О 3 e Q- ГО l™ CD * cr 2 \o о о с: го Q- CD GE CD e ro 3 Й о X о го О-

*

*

*

*

Q-> о: 3 X CD d CD О ГО X 3 3 ZT 3 ^ о CD 03 X 3 о X ^ о го

сё

со"

о> со со со

g

СМ LO о Ю

Го

см

от

а> со со со о

со"

от

СМ

g"

8

см"

от

1

о о со см со

”.

”.

g

CM co o> CM

*

*

*

*

”.

CD_

еГ со см га

g

а> со со со

со

g

от

от см от

g

со"

Г-,

от

о>_

”.

1

со о см

го

го

го"

g"

От

co CM

*

*

*

*

со

g"

со

о со га см

g

еГ о> со

S

от"

со.

о от см Ю

со.

со.

со.

CD

от

со"

го"

1

со о? о о со

со"

”.

со"

см

го"

CM

*

*

*

*

g"

ОТ

S

со о о>

g

о о>

g"

от

со.

LO LO см Ю

со.

8

го"

СМ

см"

го"

1

о со со см

от

го"

”.

го

го

a> co co CM

*

*

*

*

см

СО

8

со со со

g

а> о? со со

со

со.

го"

от со

со.

g

со.

ГО

cd"

1

m со со

го

го"

го"

го"

cd"

co co co co

*

*

*

*

со

от"

от"

о со со га

§

о о см

от"

со

см"

со га от со

со.

со"

от

ОТ.

го

cd"

1

со го LO

го"

го"

го"

”.

CM co CM

*

*

*

*

со"

со со

g

LO оГ о> см

со"

со.

со"

со оГ со со

от

го"

CD

со"

”.

1

LO LO

g"

CD

го"

1

co о о co

*

*

*

*

от

От

m со см

g

со оГ LO со

от"

го"

LO со Ю см

от

от

см

го"

cd"

1

го го со

”.

”.

1

co co о га

*

*

*

*

со о> со

g

со о> га

га

CD

LO

со LO см см

со

го

см"

от"

”.

от"

1

о со

LQ

га

га

ю

1

co eT o> co co

*

*

*

*

га

со га со о

о g I 1 Й S

1— Q-о с о 3 о 3 X о X го Q-X о о 03 го Q-GE го 03 3 3 J 3 1™ о о 03 X 3 о X 1™ о СЕ 2 LQ

^Е VI VI

^Е VI VI

^Е VI VI

о 3 X го 03 о го го о. \о о 03 3 3 J 3 h-о о 03 X 3 о X h-о X СЕ 2 LQ

VI VI

VI VI

VI VI

VI га

VI VI

VI га

VI VI

^E VI VI

^ 03 3 3 J 3 1— о о 03 X 3 о X 1— о X ЕТ 2 LQ

^Е VI VI

^Е VI VI

^Е VI VI

^Е VI VI

^Е VI VI

о о s

VI VI

VI VI

VI VI

о о S

VI VI

^Е VI VI

VI VI

о о S

со

го g

g ГО [="

го g 1 Й

о

го го f го го ZE

го го f g

-его 3 g

го го н- СП

g го g S ci

ro 5 Й

го

"1" 1 5

в g |2?

го g в g

S g го g g го [="

о 3 X о X го Q-X О о 03 го Q-ЕТ ГО 03 3 3 J 3 1™ о CD 03 X 3 о X 1™ о X ЕТ 2 LQ

о 3 X го 03 о го го Q-\о о 03 3 3 J 3 1™ о CD 03 X 3 о X 1™ о X ЕТ 2 LQ

03 3 3 3 I-о CD 03 X 3 о X 1™ о ЕТ 2 LQ

о 3 X о X го Q-X О о 03 го Q-ЕТ ГО 03 3 3 J 3 1™ о CD 03 X 3 о X 1™ о го

о 3 X го 03 о го го Q-\о О 03 3 3 J 3 1™ о CD 03 X 3 о X 1™ о го

X 5: о 3 Q- 1— ^ 03 3 3 3 1™ о CD 03 X 3 о X 1™ о го

Продолжение таблицы 1

g

co

О El О e X 1™ о El 2 \o о X 03 X X X о 03 1™ о Q-ГО СТ О о X X с: го 3 о. о 1— 3 о. о. о 1— 3 CL > го 1™ о * ЕТ 2 \о о о X го 03 о о. 3 ЕТ 3 5 О X о й о X о го О-

см со сп сп см

о о см со

от

8

8

от

8

1

от

от

о со см со

от

8

о>.

со"

см со см со о со

Q-> о о е- X X 1— о * с[ 2 \о о X 03 X X X о 03 ^ о о. го о о 3 е Q- го 1— о X ЕТ 2 \о о о го о. о ЕТ о ■его 3 й о X о го О-

со"

От

СО ГО го см

Q-> о: 3 X о с: о о го X 3 3 J 3 1— о о 03 X 3 о X 1— о го

8

8

о со см о со

га v? о га ^ ° | S I g ГМ s га -С га Е 1 ZD g га □а t™? о Н § о   § DC vd 1 с s 15 e ^ ® о § з ° Я 5 5 g га    ^ У1 и c ci о га аз 5 ^" га х S У- 2 от о g X 8 X q 3 ci га ci от   ° cl о S СТ?? га Й га га ^ л= CI |- гм е § В S КГ Ч >3   g о Я ° . в ^^ 5 2 га S’ ” о g га a-S ^ g ч о 2 о 5 га ® “ 1 J'S Й | 1 Х§ ° 1 1 | I

о

см ГО о> см

8

8

со го го го см

от

ОТ

СО

от

со

1

8

8

LO со со со со

со"

<

о го го го го

со

8

а> еГ о> со

от

от

от"

со еГ го го со

co

со со со см

со"

от"

о го го см

со"

От

1

от

от

1

от

от

о со со со со

8

8

от"

8"

со со о го

о"

со"

от"

со со

8

со"

о о см со

о

S см

со

о го со го см

8

^

1

8

S

1

от

от

го со го

со"

От

S

8

со со го

о"

со еГ о го

8

8

8

го со о го со

о

о со со см

8

со"

см го ГО го см

от

От

1

от

8"

1

со"

от

а? со го

§

от"

§

от"

о о го о го

*

*

*

*

со

со"

m о о со

о

см ГО сп о со см

со"

от

еГ о со см

от

со

8

со"

8

1

От

8

а> со со см

от

от"

8"

со"

см со со со о го

*

*

*

*

8

от

8

S го о см

о

о еГ со см

8

Si

о со го

со

от

8

со

1

8

от

го о со см

от

о

от"

от"

го о со со го

*

*

*

*

8

8

о с? со со см

о

о со о ГО

От

8

го о о го го

8

от

от

от"

от"

1

от

см

от

со"

^г

см го см го

*

*

*

*

со о со со см

CD

со го

ю

СО

го го го

от

От

от

От

от

1

от"

Si

го

а> со а>

го

о>

ОО

со-

го го о го см

*

*

*

*

о"

m со о о см

о га

1— о. о с о 3 о 3 X о X го о. X о о 03 го о. ЕТ со 03 3 3 J 3 1— о о 03 X 3 о X h-о X ЕТ 2 LQ

^Е VI VI

^Е VI VI

о 3 X го 03 о со го о. \о о 03 3 3 J 3 1— о о 03 X 3 о X h-о X ЕТ 2 LQ

VI VI

VI VI

VI VI

VI ОО

VI VI

VI ОО

VI VI

Е VI VI

^Е VI VI

g-с: 5 03 3 3 J 3 ^ о о аз X 3 о X 1— о X ЕТ 2 LQ

^Е VI VI

^Е VI VI

^Е VI VI

^Е VI VI

^Е VI VI

о о S

VI VI

VI VI

VI VI

о о S

^Е VI VI

^Е VI VI

^Е VI VI

о о S

СО

05

га g 1 Й

о

g g S о го "8" га о с! g га

га го -е-g

-е-га 3 g Й

го го -е й

го g cl п 1

го 5 й

g го 5 g го Й

го

"1" 1 5

g g |2

го 5 g g й

^ "1" го g g го Й

1— о. О с о 3 о 3 X о X го о. X о о 03 го о. ЕТ го 03 3 3 J 3 1— о о 03 X 3 о X 1— о X ЕТ 2 LQ

о 3 X го аз О го го о. \о о 03 3 3 J 3 1— о о 03 X 3 о X 1— о X ЕТ 2 LQ

g-с: 5 03 3 3 J 3 ио о аз X 3 о X 1— о X ЕТ 2 LQ

g га

га

1 га

s	g	g"		co		g	m		g
g		g"	co	g		s	g		§
g	g	co	o>		CD	g	g		g
g	oo	co			co"	g	§		g
	g	co	s	csl		g	§		s
g	g	co	s	g	CD	g	g		CD
§	oo	co	g"	co	CD	g	g		g
g	g	g	co_	co	Si	co	g		g
g	s	cS		CM	g"	co	g		CO
g	LO	co	g	CM	g"	LQ			g
g 03	S 1 g 03 co	8 1 g s s 3 g g	1 3 cl g g g 5 | s? о g	s g co	g	g g	g g s <3	g g g s ф Ф g 3 re g s s	g g -eg S s

На рисунках 8–10 представлены результаты прогнозирования инвестиций в социальную сферу УР на период 2019–2023 гг. На рисунке 11 приведен график сходимости к 1% уровню погрешности.

Отклонение модельных значений инвестиций от фактических данных по УР за 2000–2018 гг. в здравоохранение составляет 1,4%, образование – 1,2%, культуру – 1,1%.

На основе формулы (10) рассчитана величина ЧК УР за период 2000–2018 гг. Результаты расчета величины ЧК УР за 2000–2018 годы и решения задачи, связанной с прогнозированием величины и динамики ЧК, с использованием результатов решения задачи прогнозирования объемов инвестиций в ЧК на основе нейросетевого моделирования на период 2019– 2023 гг. представлены на рисунке 12 .

Рис. 8. Динамика инвестиций в образование УР за 2000–2018 гг. и их прогноз на 2019–2023 гг.: бюджетные (1), частные (2)

G 1 ·10^-6 , Р 1 ·10^-6, руб.

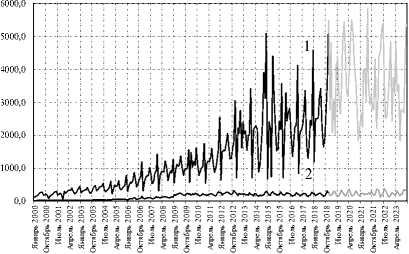
t , год

Источник: разработано авторами.

Рис. 9. Динамика инвестиций в здравоохранение УР за 2000–2018 гг. и их прогноз на 2019–2023 гг.: бюджетные (1), частные (2)

G 2 ·10^-6 , Р 2 ·10^-6, руб. 6000,0

5000,0

4000,0

3000,0

2000,0

1000,0

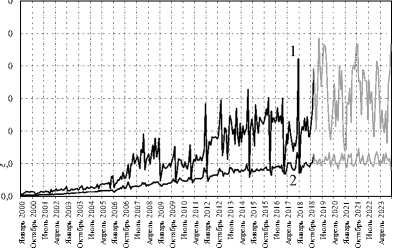
t , год

Источник: разработано авторами.

Рис. 10. Динамика инвестиций в культуру УР за 2000–2018 гг. и их прогноз на 2019–2023 гг.: бюджетные (1), частные (2)

G 3 ·10^-6 , Р 3 ·10^-6, руб. 6000,0

5000,0

4000,0

3000,0

2000,0

1000,0

0,0

Источник: разработано авторами.

t , год

Рис. 11. Зависимость показателя качества обучения нейронной сети от числа итераций

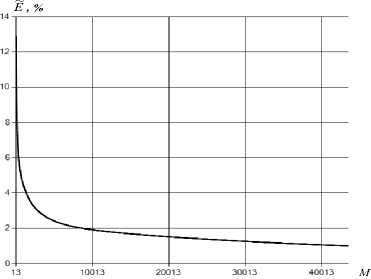
Источник: разработано авторами.

Рис. 12. Динамика человеческого капитала (а) и удельной величины ЧК (б) УР за 2000–2018 гг. и его прогноз на 2019–2023 гг. в сопоставимых ценах

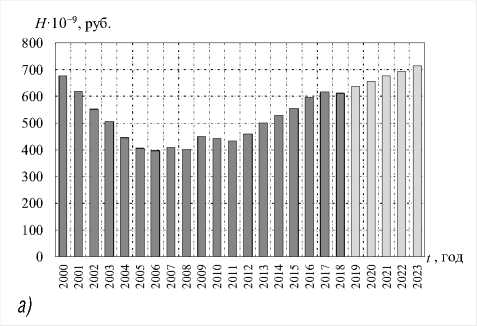
Источник: разработано авторами.

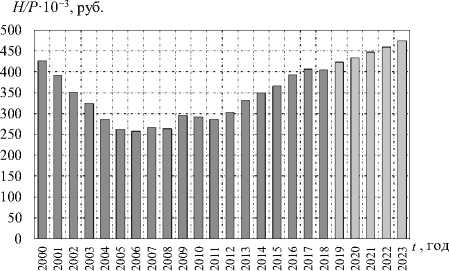
б)

Заключение

Построен нейросетевой алгоритм, на основе которого решена задача прогнозирования человеческого капитала на примере социально-экономической системы Удмуртской Республики.

Нейросетевое моделирование прогнозных значений объемов инвестиций в человеческий капитал показало свою эффективность. Так, отклонение модельных значений инвестиций в составляющие ЧК УР от фактических данных за период 2000–2018 гг. составило 1,4%.

Расчеты свидетельствуют, что величина человеческого капитала Удмуртской Республики снижалась в интервале 2000–2006 гг., в дальнейшем наблюдается рост этого показателя. Наибольшие темпы роста изучаемый показатель демонстрирует с 2013 года, прогнозируется его дальнейшее увеличение. В 2018 году размер ЧК на одного жителя УР составил порядка 400 тыс. руб.

Полученные результаты качественно коррелируют с динамикой изменения индекса человеческого развития России, определяемого специалистами ООН, который с 2000 по 2012 год возрос от значения 0,71 до 0,79 и в дальнейшем, вплоть до 2017 года, оставался практически постоянным, близким к значению 0,80.

Удмуртская Республика по многим социально-экономическим показателям является типичным регионом России ² и характеризуется их среднероссийскими значениями, поэтому результаты и выводы, полученные в ходе исследования, можно экстраполировать на РФ в целом.

Предложенная методика расчета и прогноза величины, структуры и динамики человеческого капитала может быть использована для оценки и сравнения социально-экономического положения регионов Российской Федерации.