Оценка теплового состояния стального цилиндра с термозащитным покрытием, нагруженного высокотемпературным тепловым импульсом

Функционирование и ресурс современных газодинамических импульсных устройств (ГИУ), работающих в условиях высокотемпературного нагружения (при температурах, достигающих 3500 К), обеспечивается защитой поверхностей каналов тугоплавкими покрытиями, толщиной от нескольких до сотен микрон. Как

• -    температурой плавления - Т_пл=2129 К;

• -    теплоемкостью - с=0,46 кДж/кг;

• -    плотностью - р =7190 кг/м³;

• -    коэффициентом теплопроводности – Л=93,9 Вт/(м К).

Произведем оценку его теплозащитных свойств исходя из решения задачи теплопровод- правило, в качестве теплозащитного покрытия (ТЗП) в ГИУ применяют хром, теплофизические свойства которого определяются следующими физическими величинами:

ности в возможных условиях его применения.

Задача расчета температурного поля внутри полого бесконечного цилиндрического тела, внутренняя поверхность которого подвержена нагреву равномерно распределённым по поверхности источником тепла, сводится к решению одномерного уравнения теплопроводности, представленного линейным дифференциальным уравнением второго порядка [1]:

л(т_гг +1Т_Г) = рсТ,           (1)

\ т )

где обозначено:

«L-г,., 01=^.

Ot       От       От2

Математическая постановка задачи процесса теплопередачи в цилиндре, состоящем из двух слоев с различными теплофизическими свойствами (рисунок 1) имеет вид:

Я 1 (г_1гг + |г_1г) = p₁c₁T₁ t , 0 <  т < h, t > 0;                         (2)

Я 2 (г_2гг +1T_2r) = P 1 C 1 T₂ t , h <  т < Н, t >  0.                         (3)

Для определения, температурного поля в теле в любой момент времени Т 1 (т, t), Т₂ (т, t), нужно знать распределение температуры в начальный момент времени (начальное условие) и характер взаимодействия тела с окружающей средой (граничные условия).

Начальные условия можно записать из условия термодинамического равновесия

Т 1 (т,0) = Т 2 (т,0) = Г_С р.        (4)

Будем считать известными темпера ^тУРУ среды ^Тср|_№г=0) ^{и T}пг^|(t,r=0) ^, В этом случае следует задать граничные условия 3го рода, определяющие закон теплообмена с окружающей средой на границах цилиндра для любого момента времени. Исходя из порядка старшей производной необходимо определение двух граничных условий по координате т для каждого слоя стенки цилиндра :

• Я1T1rl(t,r=0) = «пг[Tвl(ьr=0)-TпГ];(5)

• Л2Т2Г\(^Г=Н) = аср[Тн1(гг=н) — Тср];(6)

^1Т1г\^-н)=^2Т2т\^);

Г1l(t,r=ft) = Г2|(t,r=ft).(8)

где     а _пг, а _ср - коэффициенты теплоотдачи,

Вт/(м²- ° С) на внутренней и внешней поверхностях цилиндра, соответственно;

Твн, Тср - температура окружающей цилиндр среды на внутренней внешней поверхностях цилиндра, соответственно;

Н - толщина стенки цилиндра.

Н = Д з - « 1 ;            (9)

• h - известная толщина защитного покрытия.

  

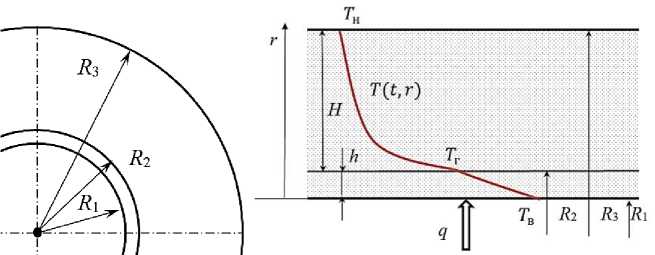
  Рисунок 1 - Расчетная схема процесса

  
  

Решение дифференциальных уравнений в частных производных произведем в MATLAB с использованием пакета PDE Toolbox (Partial Differential Equation Toolbox), реализующий решения систем уравнений в частных производных методом конечных элементов [2].

Основным объектом в Toolbox PDE является уравнение эллиптического типа, которое может быть представлено в двух эквивалентных формах

• — Р • (dPu) + au = /;

—div(cgтadu) + au = /      (10)

Коэффициенты c, a, f могут быть функциями координат и зависимой переменной u. В последнем случае уравнение будет нелинейным.

Можно решать также параболические уравнения (2, 3), представив их применительно к задачам теплообмена c зависящими от времени t коэффициентами:

р^—7•(Л7T) + аT = Q, или P • с^- — div(ЛgтadT) + аТ = Q,

где Q - объёмная мощность внутренних источников теплоты;

аТ - представляет отвод теплоты в окружающую среду с нулевой температурой, или специальный вид внутреннего источника (стока) теплоты.

На внешних границах dΩ области поставим граничные условия условие Дирихле:

TU = T_o,       (12)

а на внутренней используем обобщенное условие Неймана:

• и • (AgradT) — a(Tг — T) = 0,     (13)

^

где и - внешняя нормаль к поверхности тела.

Для поставленной задачи будем считать известной

Условие (13) описывает теплообмен с потоком газов (условие 3-го рода, согласно принятым в MATLAB формальных обозначений а -коэффициент теплоотдачи;).

Решение уравнений в частных производных в MATLAB проведем с помощью функции pdepe, которая решает нестационарные параболические и эллиптические одномерные уравнение, записанные в следующем виде

Л(х, t, T, Tx)Tt = %-m(%-m,/(%, t, T, Tx)) + s(x,t,T,Tx) (14)

Для несимметричных задач m = 0, в случае цилиндрической симметрии m = 1, для сферической симметрии m = 2. Начальное условие при t = 0 имеет вид u ( t 0 , x ) = u 0 ( x ).

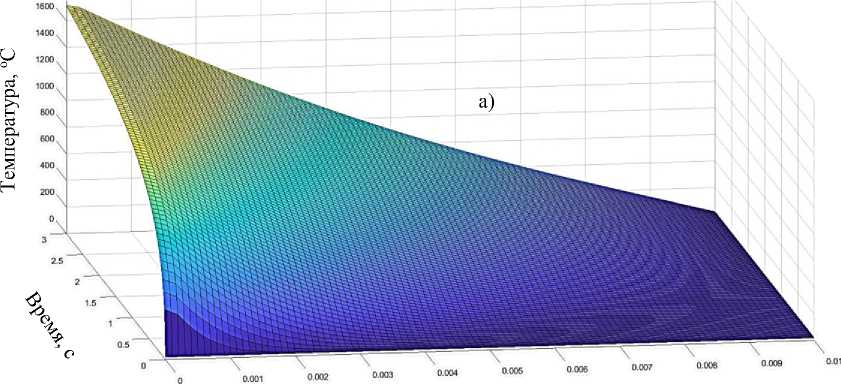
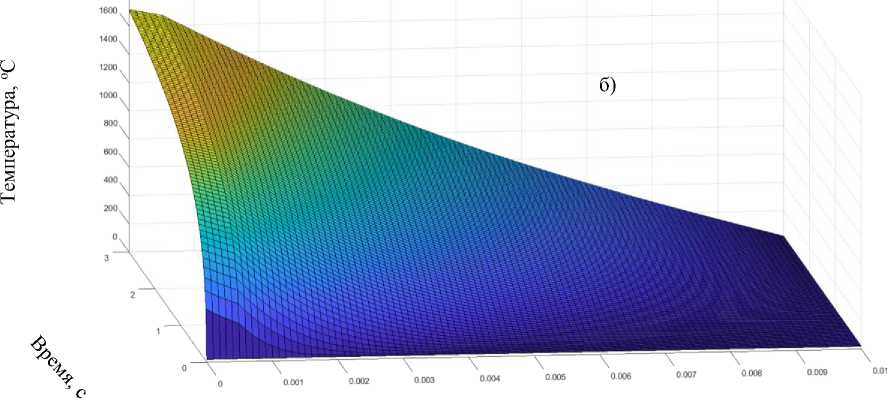
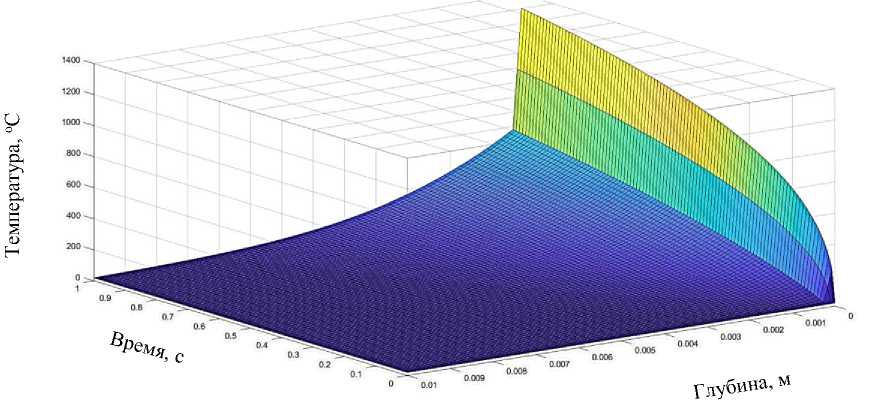
На рисунке 2 представлены трехмерные графики, иллюстрирующие изменение температуры в стенке трубы, выполненной из стали 38ХН3МФА, с защитным хромовым покрытием толщиной (а) 200 мкм и 500 мкм соответственно.

Глубина, м

Глубина, м

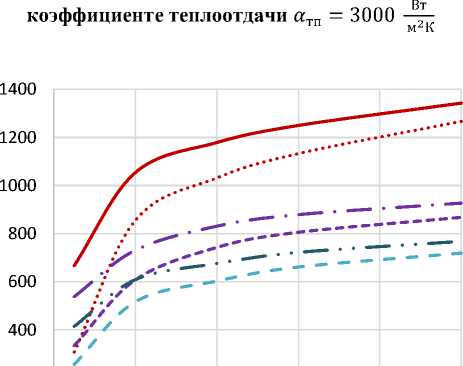
Рисунок 2 – Графики изменения температуры стенки трубы во времени по глубине при коэффици-Вт енте теплоотдачи атп = 4000 -^ и температуре газов Тг =3000 оС: а) - для покрытия, толщиной 0,2 мм;

: б) – для покрытия, толщиной 0,5 мм

Из графиков видно, что в условиях функционирования ГИУ, когда сохраняется постоянный во времени коэффициент теплоотдачи Вт атп = 4000 —— и температура газов, омывающих поверхность Тг =3000 оС, эффективность защитного покрытия невысокая. Температура в стенке под покрытием незначительно отличается от температуры, омываемой газами поверхности.

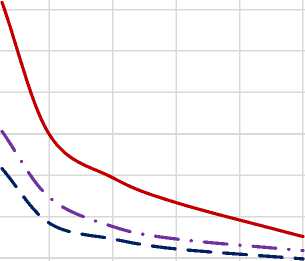
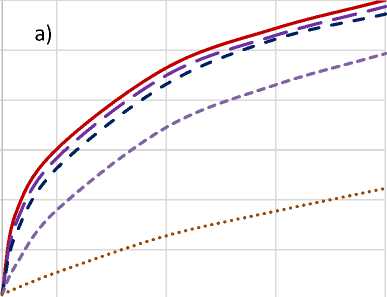
На рисунках 3 – 5 приведены тестовые примеры, из которых следует, что эффективность теплозащитных свойств хромового покрытия возрастает при увеличении его толщины, что очевидно, а также увеличивается с уменьшением времени процесса. Значимое влияние на эффективность термозащитного покрытия оказывает также значение коэффициента теплоотдачи атп.

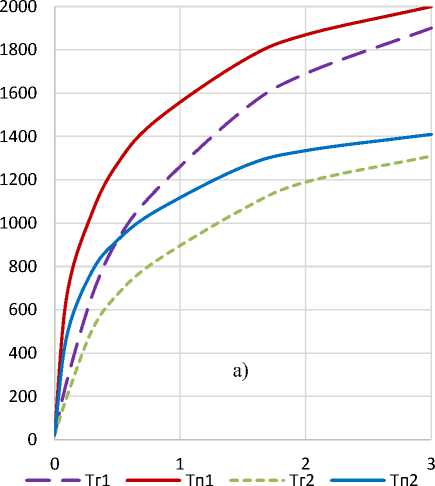
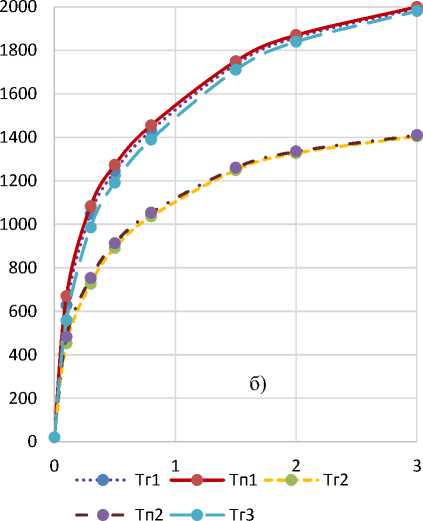
Рисунок 3 – Изменение температуры стенки: а) – на глубине 0,1 мм; б) – под покрытием; Тп1 – температура поверхности при температуре газов 3500 ^оС; Тп2 – температура поверхности при температуре газов 2500 ^оС; Тг1 – температура на глубине при температуре газов 3500 ^оС; Тг2 – температура на глубине при температуре газов 2500 ^оС; Тп1, Тг, Тп2, Тг2 – толщина защитного покрытия H=0,2 мм; Тг3 – температура на глубине при температуре газов 3500 ^оС и толщине защитного покрытия H=0,5 мм.

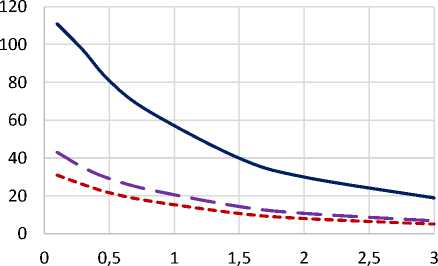
dT1         dT2        dT3

Рисунок 4 – Падение температуры под покрытием при: dT1 -при температуре газов Тг=3500 ^оС и толщине защитного покрытия H =0,2 мм; dТ2 – при температуре газов 2500 ^оС , H =0,2 мм; dТ3 – при температуре газов 3500 ^оС, H =0,5 мм;

В качестве анализа применимости хромового теплозащитного покрытия проведем его оценку для стволов современных артиллерийских орудий, время теплового воздействия у которых исчисляется долями секунды, а коэффициент теплоотдачи может достигать 200 кВт/(м2 К) [3]. Приведенные на рисунках 6 – 7 результаты расчетов показывают, что несмотря на эффективность хромового защитного покрытия, существуют ограничения его применения, обусловленные достижением температуры под покрытием выше критической точки Ас1 (Ас3), при которой возможны фазовые превращения в стали и, следовательно, нарушение целостности покрытия

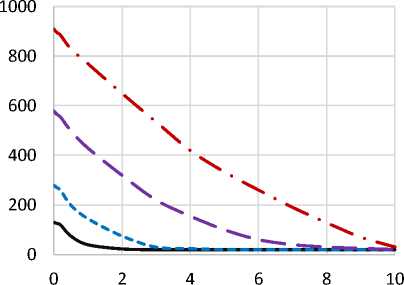
t=0,12 c        t=0,6 c t=2,0 c          t=2,0 c

давлениям, контактным напряжениям и испытывает значительные упругие деформации, которые могут приводить к растрескиванию ТЗП. В случае если его модуль упругости выше, чем у стали, то напряжения в ТЗП будут расти пропорционально и достигать больших значений. Поэтому выбор материала ТЗП и способа его формирования на защищаемой поверхности должен определяться условиями эксплуатации.

Рисунок 5 - Распределение температуры Т, К по толщине стенки трубы в различное время t при

0     0,01   0,02   0,03   0,04   0,05   0,06

dT1        dT2        dT3

Рисунок 7 – Падение температуры под покрытием при: dT1 - Тг=1730 ^оС , «_тп = 90000 -Вт-;

м2К dT2 - Тг=1150 оС , «тп = 88000 -ВТ-;;

м2К dT3 - Тг=1000 оС , «тп = 70000 -^;

0       0,01      0,02      0,03      0,04      0,05

Tг1

Tп1        Tг2

Tп2       Тг3        Тп3

Рисунок 6 - Изменение температуры стенки во времени: Тп - температура поверхности; Тг - температура под покрытием; Тп1, Тг1 – Tг=1730 ^оС , «_тп = 90000    ; Тп2, Тг2 - Тг=1150 ^оС , «_тп =

88000 -ВТ-; Тп3, Тг3 - Тг=1000 оС , «_тп = м²К

Вт

70000 -Т- м2К

Выбор в качестве ТЗП хромового покрытия обусловлен, прежде всего, относительно простой технологией его нанесения гальваническим способом, а также условиями эксплуатации ГИУ, труба которых подвержена высоким

Как правило к ТЗП предъявляется целый комплекс свойств [4], среди которых, помимо требования к модулю упругости:

• -    высокая термостойкость и стойкость к окислению;

• -    высокая адгезия к защищаемой поверхности;

• -    отсутствие образования интерметаллических и других химических соединений на границе ТЗП с подложкой;

• -    близость температурных коэффициентов линейного расширения (ТКЛР) к основному материалу;

• -    другие, способствующие стойкости ТЗП и выполнению защитных функций.

Во многих случаях обеспечить весь комплекс функций ТЗП путем нанесения однослойного покрытия не удается. Приходится формировать на защищаемой поверхности многослойное покрытие, каждый из слоев которого соот- ветствует отдельному требованию, обеспечивающему функционирование ТЗП в индивидуальных условиях, например, таким как: адгезии, препятствию диффузии, препятствию коррозии, термической защиты, контактной прочности и др..

Наиболее часто применяемыми материалами для формирования ТЗП являются карбиды, оксиды нитриды и бориды. Некоторые из них приведены в таблице 1 [5].

Таблица 1 – Коэффициенты термического расширения оксидных и нитридных покрытий

Материал покрытия	ТКЛР , 106 K–1
А1 2 О 3	8–9
СоО	15
Сr 2 O 3	7–7,8,9,6
MgO	12,9–13,9
MgO – A1 2 O 3 (шпинель)	9,1
NiO	14–17,1
SiO 2	3
ZrO 2	8–10
ZrO 2 + MgO	10 – 12
SiAlON	33,2
Si 3 N 4	3
SiC	3,7–4,8

Для быстропротекающих процессов, подобных происходящим в ГИУ характерно быстрое нагревание и охлаждение поверхности – термоудар, что при большой разности КТЛР

ТЗП и основного металла также приведет к дополнительным термическим напряжениям и разрушению покрытия. Например для сталей, ТКЛР будет изменяться от 10 до 18·10-6 К-1 при температуре от 27 до 100°С до 24,6·10-6 К-при 900 – 1000°С, что значительно превышает значения представленные в таблице 1.

Проблему, связанную с растрескиванием, в некоторых случаях удается решить путем создания самозалечивающихся покрытий. Например, трехслойное покрытие стали AISI 321, состоящее из внешнего слоя ZrO 2 , промежуточного слоя Cr + ZrO 2 и внутреннего слоя Cu-Ni показало высокую термическую стойкость при температуре 2300 °С на форсунках в камерах сгорания, в колоннах для проведения крекинг-процесса [5]. В настоящее время тонкие (>0,5 мм) ТЗП применяются в газовых турбинах и для защиты головок поршней и клапанов дизельных двигателей и двигателей внутреннего сгорания. Такие покрытия имеют, обеспечивающий адгезию и защиту от окисления внутренний слой Ni-Cr, Ni-Al или MeCrAlY и, обеспечивающий термическую стойкость внешний, ZrO2 или MgZrO3.

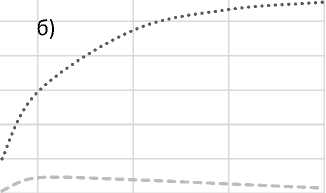
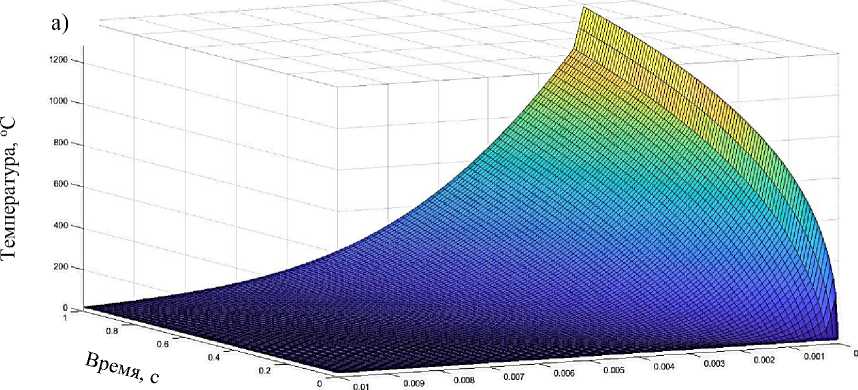
Результаты расчетного анализа термозащитных свойств ТЗП, толщиной 0,2 мм приведены на рисунках 8 и 9. Из полученных результатов следует, что ТЗП, сформированные из оксида алюминия и диоксида хрома во много раз превосходят по теплозащитным свойствам хромовое покрытие.

-0,1           0,1           0,3           0,5           0,7

-0,1

-------Tn--Cr---TiN

Al2O3       CrO2

0,1         0,3         0,5         0,7

dCr           dTiN dAl2O3       dCrO2

Рисунок 8 – Изменение температуры под слоем ТЗП, выполненного из: Cr – хрома; TiN – мононитрида титана; Al 2 O 3 – оксида алюминия; CrO 2 – диоксида хрома (T п – температура поверхности) ; а) – график температуры, ^оС; б) график разности температур снаружи и под покрытием

а)

Глубина, м

Рисунок 9 – Графики изменения температуры стенки трубы во времени по глубине при коэффициенте теплоотдачи а_тп = 4000 -Вт- и температуре газов Т =3000 ^оС для покрытия, толщиной 0,2 мм из: а) '“            м²К

–оксида хрома CrO 2 ; : б) – оксида алюминия Al 2 O 3