Оценка точности аппроксимаций, полученных методом конечных элементов

должны совпадать. Для этого введем функции округления: L x J - функция пола, которая опре-деля ется как наибольшее целое, меньшее или равное х, а именно L x J = n о x - 1 < n <  x; M - функция потолка, которая определяется как наименьшее целое, большее или равное x, а именно L x J = n о х < n <  х +1. Используя эти функции округления, введем семейство кусочно-линейных непрерывных функций следующего вида:

u ( x ) = { L Ф ( x — a ) J — M x — b ) ! } '

/,    \ x — a c + (d — c) •----- b — a

,

где ф (x) - функция Хэвисайда, единичная ступенчатая функция, чьё значение равно нулю

для отрицательных аргументов, единице для положительных аргументов и 1/2 в нулевой точке; a, b – интервал окна функции u(x), на котором она отлична от нуля (a ≤ b); c, d – параметры уравнения прямой на интервале a, b.

Функция u(x) на границах интервала (a, b) обращается в ноль. Используем (1) для описания пробной функции на произвольном интервале, задаваемом полушириной h = (b – a)/2 одномер-

ного единичного конечного элемента относи-

тельно узла Xi. В этом случае параметры кусочно-линейной непрерывной функции (1) соответственно равны a = Xi - h, b = Xi + h, c = 0, d = 1, а функция приобретает вид:

v . ⁽ x ) = ' ^ф [ x ^— ( X . ^— h ^)] J ^— Г ^ф( x ^— X. ) !} • ^{x +} h, X ‘ ⁺ h

+

{ Г ф ( x — X . ) ^ — L ф [ x — ( X . + h ) ]_ } •

h — x + X i h

Функции φi(x) изображаются в виде

ломаных и определяются конечным числом

параметров – своими узловыми значениями, отличными от нуля в пределах небольшого числа элементов вблизи узла Xi. Поскольку

u(x) по своему физическому смыслу должна быть непрерывной функцией, выберем φi(x) в виде кусочно-линейных функций, отличных от нуля на двух соседних элементах относительно выбранного. Каждая такая функция φi(x), i = 0, 1, 2, …, n-1, равна единице в Xi и нулю во всех остальных узлах. При этом набор функций u(x) будет состоять из непрерывных функций, линейных в пределах элементов с изломами в узлах и определяемых своими узловыми значениями u i . Каждую из таких функций можно изобразить в виде ломаной линии. Метод конечных элементов заменяет задачу отыскания функции на задачу отыскания кон ечного числа ее приближенных значений в отдельных точках-узлах. При этом, если исходная задача относительно функции состоит из дифференциального уравнения с соответствующими граничными условиями, то задача метода конечных элементов относи -тельно ее значений в узлах представляет собой систему алгебраических уравнений. С уменьшением максимального размера элементов увеличивается число узлов и неизвестных узловых параметров. Вместе с этим повышается возможность более точно удовлетв орить уравнениям задачи и тем самым приблизиться к искомой функции. Рассмотрим применение метода для описания одномерного профиля. В этом случае пробная функция, определяемая уравнением (3), представлена линейной комбинацией функций (2) с коэффициентами u i :

n - 1

u (x )=У ui • фХ x)     (3)

i = 0

, где n – число конечных элементов, аппроксимирующих континуальную зависимость на заданном интервале. Пусть на концах интервала Xmin…Xmax функция (3) обращается в нуль, а на рассматриваемом промежутке равна единице. В этом случае приравниваем функцию (3) этой величине:

n - 1

У u i • ф,⁽ x ) = ¹      (4)

i =0                             ^{V 7}

X max

J

X min

n - 1

ф, ⁽ x УУ u i ■ фЛ x )

.                    i =0                         .

Xmax dx = J ф j (x )dx

X min

При этом определенные интегралы име-

ют простые алгебраические выражения во всех

узлах X i на интервале существования решения:

X max

J

x min

n - 1

фАx)-У ui ■ ф,(x)

.               i =0                   .

' 0, i <  j - 1

I , i = j - 1

,         2 , dx = — - h, i = j

h

6-ⁱ = j + ¹

, 0, i >  j + 1

X max

J ф j ( x ) dx = h

X ■ min

где h = (Xmin - Xmax)/(n + 1) – полуширина конечного элемента. Используя соотношения (7) и (8) в системе уравнений (6), получаем слева трехдиагональную разреженную матрицу коэффициентов, умноженную на вектор неизвестных {u i }, а справа – вектор из элементов h:

3 2 h	h 6	0	0	0		u 0		h
h 6	32 h	h 6	0	0		u 1		h
0	h 6	32 h	h 6	0	•	u 2	=	h	(9)
0	0	h 6	3 2 h	h 6		u n - 2		h
0	0	0	h 6	3 2 h		u n - 1		h

Умножая левую и правую часть матричного уравнения (9) на (1/h), получаем матричное уравнение, не использующее параметр (h):

2 3	1 6	0	0	0		u 1		1
1 6	2 3	1 6	0	0		u 2		1
0	1 6	2 3	1 6	0	•	u 3	=	1		(10)
0	0	1 6	2 3	1 6		u n - 1		1
0	0	0	1 6	2 3		un		1
	Очевидно,			что	вектор		в	правой		части

представляет собой значения аппроксимируемой функции, следовательно, в общем виде коэффициенты (ui) определяются следующим

матричным уравнением:

2 3	1 6	0	0	0		u 1
1 6	2 3	1 6	0	0		u 2
0	1 6	2 3	1 6	0	•	u 3
0	0	1 6	2 3	1 6		un - 1
0	0	0	1 6	2 3		un

U ( X 0 ) U ( X 1 , ) U ( X 2 ) U ( X n - 2 ) ^U ( X n - 1 )

и, умножая левую и правую часть равенства (4) на φj(x), где j = 0, 1, 2, …, n-1:

n

фj(x )-У u • ф,( x )=1- фj(x)

i = 1

интегрируем систему уравнений (5) по области существования решения Xmin … Xmax , согласно методу Галеркина получаем систему алгебраических уравнений, используемую для определения коэффициентов u i :

Здесь матрица (11) является трехдиагональной, и решение может быть получено методом Гаусса, матричным методом (умножением на обратную матрицу) или методом прогонки. Для систем малой размерности метод решения не существенен, но с увеличени ем точности решения необходимо увеличивать число конечных элементов на области существования решения, а это приводит к увеличе-

нию числа неизвестных в уравнении (11). Если требуется большая точность решения, необходимо использовать метод прогонки, позволяющий решать системы большой размерности без существенных ошибок округления. Рассмотрим применение этого метода в данном случае. Метод прогонки является двух шаговым. Вначале вычисляем вспомогательные величины a i, зависящие от элементов трехдиагональной матрицы из правой части (11):

q , =

( q - ) ² - 1 q- 2

где q0 = 4; q1 = 15. В этом случае элементы вектора (12) задаются следующими соотношениями:

а о =-- , « 1

q о

q , ... , а , =- q q 1                      q i

а о

1                     1                                    1

—, а . =--, . , a n - 1 =--

4          4 + а ₀                4 + a n - ₂

Рекуррентные соотношения (12) фактически представляют собой цепную дробь следующего вида (ряд Фарея):

Следующим этапом первого шага метода прогонки является расчет коэффициентов p i, которые для уравнения (10) (единичный прямоугольный профиль) определяются следующими соотношениями:

^а к

в о = 3, в 1 =

^{6 в} , , в

⁴ + ^а о

6 - в , - 1

^{4 + а} i - 1

4 -

4 -

Следовательно, (13) может быть представлена рекуррентной формулой, образованной следующей числовой последовательностью:

Используя соотношения Эйлера, преобразуем (16) к удобному для вычислений рекуррентному виду, образованному следующими числовыми рядами:

а _о = 3, a 1 = 6,. . , а ,

Ь о = 2, b 1 = 5, ... , b i =

Используя (17) и (18), получаем рекуррентную формулу для расчета элементов вектора (16):

в о = а , в 1 Ь о

Определив из (15) и (19) значения вспомогательных векторов, переходим ко второму

з - ( - 1 ) i

3 - ( - 1 ) i

• a i - 1 + a i - 2

• b i - 1 ⁺ b i - 2

а ,..., в , ^Ь 1

a b

шагу метода прогонки - расчету весовых коэффициентов ui по формулам:

6 - в 2                         оо un-1 = --------~ , un - 2 = а n - 2 • un-1 + вn - 2, . , u о = а о • u 1 + в о (20)

4 + а n - 2

Используя значения весовых коэффици- аппроксимацию этой функцией исходного ентов u i , для пробной функции (3) получаем единичного прямоугольного профиля:

n - 1

^(x) = E[uk • Фк(x,n)]

к = о

, где фк(х, n) определяется следующей формулой:

Ф к ( x , n ) = ф| x

2 • к + 2 , + 1

n + 1

( 2 • к + 4 ,

- Ф1 x -         + 1

I n + 1

( , n x n • x 3 |

•\k -----+- 1 +

+ Ф| x

2 • к , + 1

n + 1

_л ( 2 • к + 2 ,

- Ф| x -         + 1

I n + 1

n

•

, x n • x 1 к + — +--+ -

Интегрирование функции (21) на интервале прямоугольного профиля дает сл едую-щую числовую последовательность:

_f .= 4  f .= 6  _f .= 84  _f .= 47  _f .= 456  _f .= 90  _f .= 248  _f 3411   _f 10308  _f

² ’ 5   ³ ’   7   ⁴ ’   95 ⁵ ’   52 ⁶ ’ 497    ⁷ '   97 ⁸ ' 265 ⁹ ' 3620    ¹⁰ ' 10879 ¹¹

Таким образом, предложенный конечный элемент (22) для аппроксимации континуальных функций позволяет использовать числовые ряды для оценки точности описания континуальной функции, не прибегая к численному интегрированию. Рассмотрим данную числовую последовательность (23) в виде графика в осях {1/n – 1-f(n)} (рисунок 1).

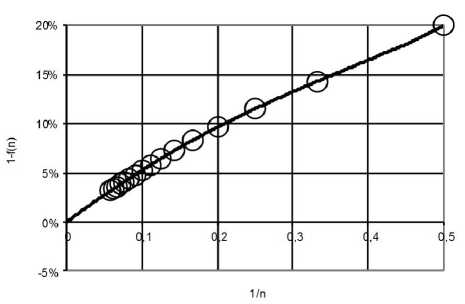
Рисунок 1 – Экстраполяция числового ряда невязок – [1-f(n)] от обратного числа конечных элементов – (1/n)

Как видно из представленного графика (рисунок 1), уравнение линии тренда (R=1) в точке ноль дает невязку, равную нулю, что соответствует числу конечных элементов стремящихся к бесконечности:

1-f(n) = 1,2749(1/n)4 - 0,603(1/n)3 -

0,347(1/n)² + 0,5649(1/n)    ⁽⁾

Следовательно, описание континуальных функций конечными элементами может дать большую точность, a урaвнение (24) является и́ нфимумом для описания одномерных континуальных функций методом конечных элементов.