Оценка точности методов математического моделирования процесса тепломассопереноса в дисперсных средах

Точные решения задач тепло массопере-носа в замкнутом виде, удаётся получить далеко не всегда. В остальных случаях точные решения либо принципиально невозможны (когда граничные условия или условия на контуре нельзя выразить в аналитической форме), либо приходится сталкиваться с таким рядом вычислений, что получени е аналитических решений становится нецелесообразным. В связи с этим при решении многих практических задач давно используются приближённые методы исследования.

Эти методы можно разбить на две основные группы. К первой относятся вариационные методы, применение которых позволяет получить численные алгоритмы и приближённые аналитические выражения искомых функций. Вторую – составляют численные методы, при использовании которых определяются значения искомых функций при тех или иных значениях аргументов.

Развитие теории тепломассопереноса, обязано, главным образом, работам академика А.В. Лыкова и его школы, что создало все возможности для широкого внедрения в инженерную практику аналитических и экспериментально-аналитических методов расчета процессов тепломассопереноса в системах с твердой фазой.

Для решения задач тепломассопереноса применяют различные методы: сеток, прямых, разделения переменных, интегральных преобразований Лапласа.

Описание динамики процесса проводится по уравнениям А. В. Лыкова [1] при допущении о бесконечно малой величине градиента общего градиента давления.

В общем виде эта задача относится к тем, где используются уравнения с переменными параметрами. В качестве таких параметров могут приниматься коэффициент теплообмена α и влагообмена β , а также коэффициент диффузии влаги a _m ( t ) , которые представлены эмпирическими коэффициентами. Математическое описание процесса сушки зерна еще усложняется, так как зерно неоднородно по структуре и составу.

Рассмотрим алгоритм решения данной задачи в аналитической форме с помощью модифицированных рядов Фурье [2, 3], а затем сравним полученное решение с решением А.В. Лыкова [1] и решением по методу прямых [4].

За основу возьмём систему уравнений А.В. Лыкова [1], представленную уравнениями в сферической системе координат в безразмерной форме:

5 T	Л f 5 2 T	2 5 T )	л f 5 2 U	2 5 U |
5т	= A 11 | TT + ( 5 r	- r 5 r )	■ A 12 | tv + ( 5 r	r 5 r J ,          (1)
5 U	, f 5 2 T	2 5 T	1 л f52 U	2 5 U )
—	= - A 21 1	+	1 + A 2 2 1	+1 ,
5т	21       2 ( 5 r	r 5 r	1 22 ( 5 r 2	r 5 r )

( U,T ) > 0 , (U,T ) <Ю при r ^ 0

r €[0, 1] , те[0, тк ], с граничными условиями третьего рода на ша-

ровой поверхности:
5 T ( r , т )	- a 1 (1 - T ( r , т )| r = 1 ) + r = 1
5 r

+ a 2 (1 - U ( r , т )| r = 1 ) = 0,

5 U ( r , т )

+ 6 1 (1 - T ( r , т )| _r = 1 ) +

-

5 r

r = 1

+62(1 - U (r, т )| r=1) = 0, с начальными условиями

T ( r, 0) = 0 , U ( r, 0) = 0 .

где комплексы критериев определяются уравнениями: A11 = 1 + £ KoLu Pn , A12 = £KoLu, A21 = LuPn ,           A22 = Lu ,           a 1 = Biq, a2 = (1 - £)KoLuBim,                61 = PnBiq ,

6 2 = Bi m (1 - (1 - £ )PnKoLu), а используемые критерии т = Fo, т _к = Fo _к - безразмерное текущее и конечное время; Ko – Коссовича; Lu – Лыкова; Pn – Поснова; Fo – число Фурье; теплообменный и массообменный критерии Био Bi_q , Bi_m .

Для решения задачи (1)-(3) будем использовать три метода:

М 1 – метод интегральных преобразований Лапласа и разложение в ряды Фурье, предложенный А.В.Лыковым и Ю.А. Михайловым;

М 2 – метод прямых [4];

М 3 – метод разложения неизвестных функций по модифицированным рядам Фурье [2, 3]. Алгоритм решения по методу М 1 приведён в [2].

Решение М 2 .

Шаг 1. С учетом того что пря-мая X k = kh , к = 1 , 2 ,...,N + 1 , где N - число внутренних прямых; h - шаг по X ; h = 1 /N , получим систему дифференциальных уравнений: для к = 1 :

'" = 4 ( ² T 2 ( т ) - 2 T ( т ) ) - A 2- ( ^{2 U} 2 ( т ) - ^{2 U} 1 ( т ) ) , и V h                       h

^ = -A (2T2 (т ) - 2T (т )) + A22 (2U2 (т ) - 2U1 (т )) ; ат h                     h для к = 2, 3,..., N :

dTX )_ All ( k + U- - I ™ (_\ к - 1j. it) (       ■ )- 2T(r)+к'

^A1, 2 (k + ¹              ~ _T     („\^{k- 1} т

-TV I T— T N + k + 2 ^(Т) - ^2TN + k + 1 ^{(T) +} T— ^TM + k ^(T) I , h ² ( к                            к )

^dU k ^{( т} ) A 1 f ^{к +} 1     _k               к ^- 1 i )

d■ x hr U + 1 ^{( r} ) ^{2 U}- ^{( r}"^{U ( т}

+ A TT Ph² Un + к + 2 ( т ) - 2 Un , к + 1 ( т ) + '' ' Um + к ( т ) ! h ² ( к                             к )

для к = N +1: dT_N,, (т)

= A _U(A T ) n + 1 - A ^(A U ) n + 1 ;

ат dUM. 1 (т)

N+1( ) = - A21 (AT) N+1 + A22 (A U) N+1, ат где

5 T И т II2 f5 T (A -A TN+1(т) - TN (т) ) (AT)n+1 = 2^(1,т) + tI t^(1 ,т)--;

5 r      h(5r             h)

( A U ) N + 1 = 2 5 U (1 , T ) + 2 ^f5 U (1 , т ) - U N ^{+ 1( т ) -} U N ^{( т )} I .

5r       h (5r              h)

Начальные условия остаются прежними:

T k |т= 0 = 0 , U k |т= 0 = 0 , к = 1 , 2 ,..,N + 1 .

Шаг 2. Производные от функций T и U на границах слоя подставляются в систему дифференциальных уравнений из граничных условий (2). Граничные условия, таким образом, находятся в системе в виде дифференциальных выражений.

Решение М 3 .

Шаг 1. Решается система обыкновенных дифференциальных уравнений:

- z ‘ + A 11 z 3 - A 1,2 z 4 = 0,

Z 2   A. 21Z з + A.2 2 Z 4 — 0, a 1 z 1 - a 2 z 2

+— z₃

M

^- a 1 ⁺ a 2 ⁺ E ^zm + 4 m ^{n ( - 1)} m m = 1

= 0,

1 ^M

-b1z 1 -62z2 --z4 + b1 + 62 - E zm+4+МШn(-1)

- A

⁺ A 12

1    2 2         ( - 1) m

- n m zm+4 +

1    2 2             ( - 1) m

X П m zm+4+M + m = 1 ..M ,

(-1) m  , z1 m n

( - 1) m + 1

⁺     3 3 ^z 3

m n

2 ^z m + 4

(-1)m  t    (-1)m+1       1 v z2 +    4 4 z4   - zm+4+M mn m3 П3      2

= 0,

+

+ A 21

1    2   2

^ ^П m z m + 4

( - 1) m

--------z 3

mn

^^^^^^^

^- A 22

1 2 2             ( - 1) m

T ^П m z m + 4 + M ⁺----- z 4

mn

= 0.

m = 1 ..M ,

с начальными условиями z_t (0) = 0 , i = 1,..., N , где M - число членов ряда, N = 2 M + 4 - общее количество уравнений.

Шаг 2. Записываем решение в общем виде:

Г 1 2 1 ) T ( r, т ) = Ф ( т ) + ф _х ( т ) l — r --I +

• V 6     6 )

• 1    M

+ X T_m( т )sin ( m n r ) ,

Г m = 1

Г 12 1 ) и(r,т) = W) + Ух(т)l -r --I +

• V 6     6 )

• 1    M_TT,„.,

+ X Um(т)sin(mnr), r m=1

где T m ( t ) = T m + 4 ( t ) , U m ( t ) = U m + 4 + m ( t ), m = 1 ..M , ф ( т ) = Z 1 ( T ), v ( t ) = z 2 ( т ), Ф 1 ( т ) = z з ( т ), У 1^(т ) = ^z 4^{( т} )•

Решение системы алгебраических и обыкновенных дифференциальных уравнений можно получить аналитически методом интегральных преобразований Лапласа или методом Эйлера, или численными методами Рунге-Кутты [5].

Средние значения потенциалов переноса теплоты и вещества в шаре в методах М 1 и М ₃ вычисляются по соотношениям:

RR

T ( t ) =    J r ² T ( r, t ) dr, U ( t ) =    J r ² U ( r, t ) dr . (4)

R ³ 0                     R ³ 0

Для сравнения решений в качестве базовых взяты значения критериев е = 0 , 5, Ko = 1 , 2 , Pn = 0 , 5 , Bi_m = 10 . Критерии Лыкова и теплообменный критерий Био выбирались из множеств Lu = {0,1; 0,3; 0,5; 0,7; 1.0} и Bi q = {1; 5; 10;15; 20} .

Проводились вычисления по программам, реализующим алгоритмы М 1 , М ₂ и М ₃ в системе Maple 9.5.

Для проведения сравнения в алгоритме А.В. Лыкова использованы корни, полученные решением характеристического уравнения в системе Maple 9.5. Результаты, полученные по программам, отличаются не более чем на 1 %. На рис. 1-3 приведен графический анализ результатов работы алгоритмов.

В табл. 1 приведены значения температуры и влагосодержания, а в табл. 2 - оценка работы методов.

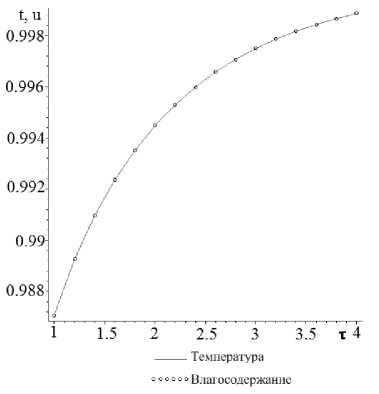
Рис. 1. Значения температуры и влагосодержания в центре зерна

----• Температура на поверхности зерна

«««««« Температура по расчёту [ 1 1

-----Влагосодержание на поверхности зерна оооооо Влагосодержание по расчёту [1]

Рис. 2. Значения температуры и влагосодержания на поверхности зерна

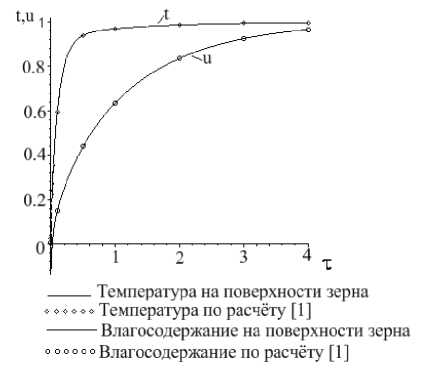
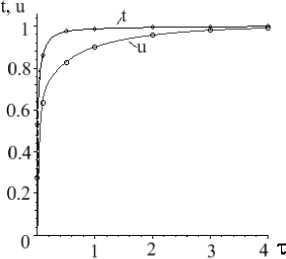
Рис. 3. Средние значения температуры и влагосо-держания на поверхности зерна

Таблица 1

Численные значения температуры и влагосодержания по методам М 1 , М 2 и М 3

т	Температура зерна ( T )			Влагосодержение зерна ( U )
	в центре	средняя	на поверхности	в центре	среднее	на поверхности
Метод А.В. Лыкова и Ю.А. Михайлова М 1
1.00	0.93814	0.96963	0.98710	0.15716	0.63533	0.89987
2.00	0.97020	0.98654	0.99448	0.58547	0.83594	0.95696
3.00	0.98632	0.99387	0.99749	0.80936	0.92514	0.98044
4.00	0.99375	0.99720	0.99885	0.91286	0.96581	0.99107
Метод прямых М 2
1.00	0.93802	0.96944	0.98710	0.16192	0.63483	0.90016
2.00	0.97032	0.98651	0.99449	0.58728	0.83540	0.95701
3.00	0.98635	0.99385	0.99749	0.80987	0.92478	0.98044
4.00	0.99375	0.99718	0.99885	0.91293	0.96558	0.99105
Метод модифицированных рядов Фурье М 3
1.00	0.93768	0.96946	0.98707	0.15689	0.63543	0.89992
2.00	0.97021	0.98655	0.99448	0.58552	0.83598	0.95697
3.00	0.98632	0.99387	0.99749	0.80941	0.92517	0.98045
4.00	0.99375	0.99720	0.99886	0.91288	0.96582	0.99107

Таблица2

Оценка работы методов в виде абсолютных отклонений и средней ошибки аппроксимации*

№	Макс. абс. отклон.	Средняя ошибка аппрок-сим., %	Сравнение методов
			Базовый М1	Расчетный
1	0.00023	0.00917	По T в центре	М 2
2	0.00046	0.00391	По T в центре	М 3
3	0.00019	0.00376	По средней T	М 2
4	0.00017	0.00160	По средней T	М 3
5	0.00003	0.00076	Πo T на по-верхн.	М 2
6	0.00003	0.00050	Πo T на по-верхн.	М 3
7	0.00476	0.49590	По U в центре	М 2
8	0.00027	0.01880	По U в центре	М 3
9	0.00061	0.05285	По среднему U	М 2
10	0.00010	0.00497	По среднему U	М 3
11	0.00029	0.00707	Πo U на по-верхн.	М 2
12	0.00005	0.00193	Πo U на по-верхн.	М 3

*В качестве экспериментальных значений приняты значения температуры и влагосодержания, вычисленные по алгоритму М₃. Сравнение результатов проводилось при т >  0 .

Проведенное исследование подтвердило пригодность применения метода модифицированных рядов Фурье для решения задач тепло-массопереноса путем сравнения с известным решением А.В. Лыкова и методом прямых.

Предлагаемый метод отличается от метода А. В. Лыкова тем, что отсутствует необходимость вычисления корней характеристического уравнения. Метод прямых требует вычисления средних значений потенциалов 28

переноса теплоты, используя квадратурные формулы, а в методах М 1 и М 3 средние значения вычисляются по соотношениям (4), что гораздо проще. Доказано, что подобные ряды Фурье обладают свойством повышенной сходимости и допускают возможность почленного дифференцирования [3].

Применение модифицированных рядов Фурье для решения подобных задач позволяет получить приближенное решение в аналитическом виде с любой точностью при минимальных вычислительных затратах на ЭВМ.