Оценка требований к точности навигационного обеспечения попадания в прямоугольную цель

Для современных операций специального назначения характерно требование знать точное местоположение объекта (цели) поражения. Одновременно требуется не поражать жилые кварталы, социальные объекты. Это ведёт к противоречивым требованиям, с одной стороны надо поразить цель, с другой стороны нельзя поражать соседние объекты. Одной из возможностей разрешения противоречия может быть применение зарядов малой мощности. Применение таких зарядов требует высокоточного попадания в цель. Точность попадания достигается точным определением местоположения цели. Определение местоположения обеспечивается навигационной аппаратурой. Отсюда вытекает важнейшее требование к этой аппаратуре - точность [1, 2]. Данная работа направлена на количественные оценки требований к точности определения местоположения прямоугольных целей.

Результаты работы могут найти применение в силовых структурах при определении требований к точности навигационной аппаратуры потребителя.

Модель попадания заряда в цель

В основу разработки моделей для определения вероятности поражения объекта высокоточным оружием W(n) в данной работе положена обобщенная модель [3]:

n

W (n ) = £ V (m ). (1)

m = 0

Эта модель позволяет отдельно рассматривать параметры, характеризующие точность применения оружия, и параметры, характеризующие мощность боеприпасов, живучесть цели и их взаимосвязь.

Точность применения оружия в данной модели характеризуется распределением числа попаданий в цель P n,m , а мощность боеприпасов и живучесть цели - условной вероятностью поражения цели G ( m ).

Распределение числа попаданий в цель P n,m зависит от числа выстрелов, распределения точек падения снарядов, поражаемого пространства цели и характера зависимости между выстрелами.

Если обозначить координаты точек падения снарядов X, Y, а поражаемое пространство цели S , то в самом общем случае вероятность попадания боеприпаса в цель может быть определена как вероятность того, что точка ( X, Y ) принадлежит области S :

p = P ( X, Y е S), (2)

Так как на точность стрельбы оказывает влияние большое число различных случайных факторов, то согласно основной предельной теореме теории вероятностей (теорема Ляпунова) с достаточной для опера- тивно-тактических расчётов точностью можно считать, что распределение точек падения снарядов подчиняется нормальному закону распределения вероятностей с плотностью [3, 4]

_     1

2(1 — r ²)

f (x, У) =-------1 I----- e

2noxov V1 - r

xy

У - y

где а_х , о - средние квадратические отклонения координат точек падения от центра

рассеивания

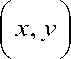
; r - коэффициент корреляции.

С учётом формул (2) и (3) вероятность попадания в цель может быть вычислена по формуле

Р = JJ f ( x, У ) dxdy .

S

В частности, вероятность попадания в цель, поражаемое пространство которой представлено в виде прямоугольника со сторонами, параллельными главным осям рассеивания (рисунок 1), может быть вычислена по формулам

Р = JJ f ( x, У ) ^dx^dy = ¹ s                ⁴

Ф

-\ b - x

- Ф

a

-\

- x

Ф

(    " 7

d - У

- Ф

(    ^-7

С - У

ox

x 7

o x k

k

°

^G y k

или по формуле

b d                        1 Р = J J f ( x, У) dxdy = 4 г Ф (.    -) b-x o - Ф (    -^ a - x o ] Ф (-^ d - У o - Ф (    -7 c-У o ] ,   (5) ac L k   x 7 k    x 7 k   У 7 k   У 7 где Ф(/) - функция Лапласа,

Ф ( ^ ) =

2 п

_г  _/ 2

J e ² dt .

о

Эти вероятности будем рассчитывать по стандартным процедурам Маткад.

y

d

c

a

Рис. 1. Прямоугольный объект поражения bx

Расчёты можно вести не через средние, а через срединные отклонения. Тогда формула

• (3)    примет вид

  e

  
  

  ^p * ( 1 - r ² )

  
  
  

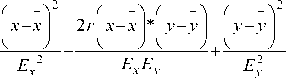
  f ⁽ x , y ) =

  
  

p p

n E E V1 - r²

xy где Ex, Ey - срединные отклонения координат; p = 0,4769 является решением уравне- ния

p

4 J e ~ x dx = П и формула (5) примет вид

1 ^p = 4

°

Ф

r,   -^

b - x

-

Ex

V x J

Ф

V

- a - x

E x

°

Ф

r-^ d - y

r

\

J

Ev

V y J

°

-Ф

c ^- y

V

E y

J

° где Ф - приведенная функция Лапласа,

°               z

Ф = 2 p f e - ^{p 2} t ² dt

П о ^J o        ^.

Функция Лапласа связана с приведенной функцией Лапласа соотношением

°

Ф ( z ) = Ф ( p /2 z ) = Ф (0,674 z ) .

Рассмотрим прямоугольник со сторонами a, b и срединной ошибкой а. Тогда вероятность попадания в этот прямоуголь- ник вычисляется по следующему алгорит му:

• 1.    Вычисляем вспомогательные величи-      2. Вычисляем вероятность попадания в

• 3.    Находим результирующую вероятность попадания в прямоугольник по формуле

ны rl = aрЛ , и r2 = bp[2 .              линии a, b по формулам y (rl) := (2prom(rl, 0,ст))-1, y (r2) := (2prom(r2,0, ст))-1.

У = У (r1) У (r2).

Например: a = 160 m, b = 385 m, ст = 160 m, y = 0,448.

По данному алгоритму были проведены расчёты. Результаты исследований приведены на рисунке 2 - 5.

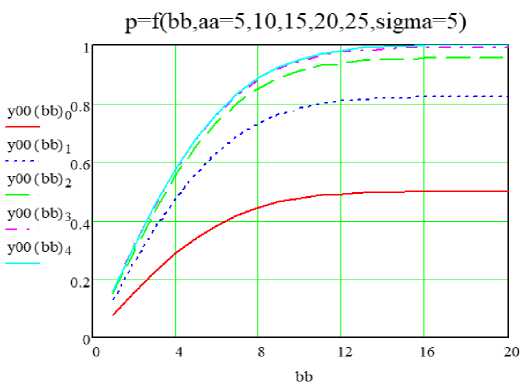
Рис. 2. Вероятность попадания в прямоугольник в зависимости от длины его сторон, сигма = 5 м

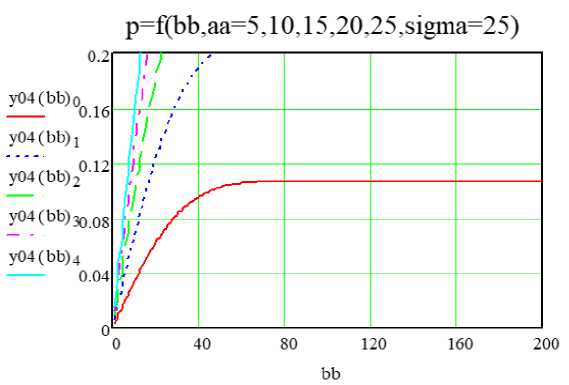
Рис. 3. Вероятность попадания в прямоугольник в зависимости от длины его сторон, сигма = 25 м

На рисунках 2 и 3 приведены результаты расчётов вероятности попадания в прямоугольник в зависимости от длины его сторон. На рисунке 2 для сигмы 5 м, на рисунке 3 для сигмы 25 м. Из рисунков сле- дует, что для попадания с вероятностью 0,95, длина обеих сторон должна быть более 3 сигм. Если одна сторона соизмерима с сигмой, то вероятность попадания не превышает 0,5 при любой длине второй стороны. Из этого следует важный для практики вывод о том, что средство стрельбы должно быть укомплектовано навигатором для наведения на объект поражения с сигмой (погрешностью) не более 1/3 меньшей стороны.

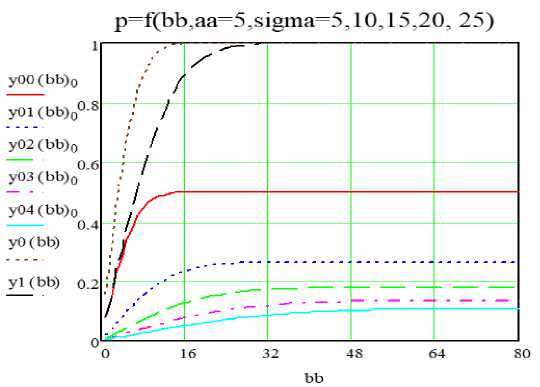
Рис. 4. Вероятность попадания в прямоугольник в зависимости от длины одной стороны,

вторая равна 5 м, при разных сигма

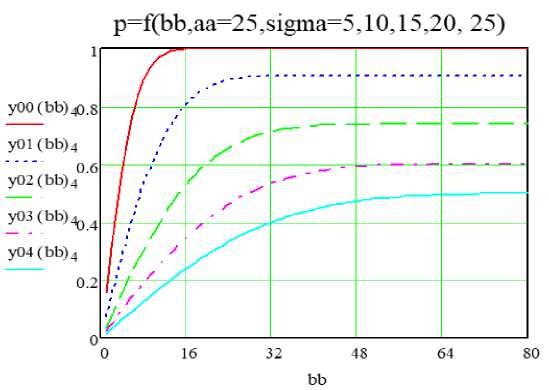
Рис. 5. Вероятность попадания в прямоугольник в зависимости от длины одной стороны, вторая равна 25 м, при разных сигма

Из рисунков 4 и 5 следует, попадание зависит только от соотношения величины сигма и длины меньшей стороны. На рисунке 4 приведены также вероятности попадания в сторону bb в зависимости от

dd(bb)

Анализ результатов исследования позволяет предположить, что вероятность попадания определяется не отношением площади к среднеквадратической погрешности сигма, а от отношения длины мень- сигмы 5 и 10 м: y0(bb) и y1(bb) соответственно. На рисунке 6 приведены зависимости отношения длины стороны dd(bb) к сигме

_ bb c .

шей стороны к сигме. Например, при длине одной стороны 1000 м, а второй 3 м, площадь равна 3000 кв. метров. Тогда для поражения цели с вероятностью не менее 0,95 точность попадания не более 1 м. То- гда как при длине сторон 30 и 100 м имеем туже площадь, а точность попадания может составлять только 10 м, а при длине сторон 60 и 50 м, достаточной будет точ ность попадания 17 м.

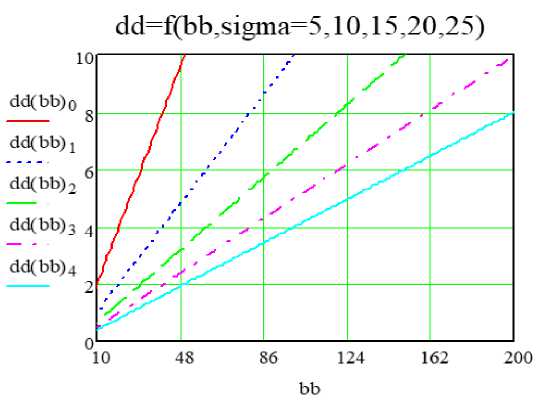
Рис. 6. Зависимость отношения длины стороны к сигме (dd(bb)) в зависимости от сигмы и от длины стороны bb

Заключение

Таким образом, для круговых целей вероятность попадания жестко связана и с радиусом цели и площадью в отличии от прямоугольной цели. Это принципиальное отличие требований к точности при попадании в круговую и прямоугольную цель.

Главный вывод из проведенных исследований, заключается в том, что вероятность попадания в прямоугольные цели ужесточает требования к точности попадания.

В дальнейших исследованиях следует оценить вероятность попадания при использовании нескольких зарядов.