Оценка упругих характеристик глазного яблока по отклику энуклеированного глаза на введение заданных объемов жидкости
Автор: Моисеева И.Н., Штейн А.А., Любимов Г.А.
Журнал: Российский журнал биомеханики @journal-biomech
Статья в выпуске: 4 (90) т.24, 2020 года.
Бесплатный доступ
Выполнено математическое моделирование деформации глазного яблока под действием внутреннего давления. Моделирование осуществлялось в рамках развиваемого авторами общего подхода, представляющего глазное яблоко как совокупность деформируемой двумерной поверхности (роговица) и нульмерного элемента, откликающегося изменением объема на изменения внутриглазного давления (склеральная область). Результаты расчетов сопоставлены с представленными в литературе экспериментальными данными, полученными на энуклеированных глазах человека. Сделан вывод, что наблюдаемая в опытах нелинейность зависимости внутриглазного объема от давления определяется нелинейностью упругого поведения роговицы, тогда как склеральная область в исследованном дипазоне давлений деформируется практически линейно. Оценены значения констант, присутствующих в модели: роговичной и склеральной жесткостей и параметра, определяющего нелинейность упругого деформирования роговицы. Значения упругих модулей оказались близки к оценкам, ранее полученным авторами на основании измерений, выполненных на живом глазу. Величина параметра нелинейности роговицы, определенная по измерениям на целом энуклеированном глазу, получилась близкой к значениям, оцененным авторами на основании данных опытов с изолированной роговицей, но в среднем несколько ниже. Индивидуальные значения всех упругих параметров для конкретных обследованных глаз заметно различаются между собой.
Энуклеированный глаз, роговица, склера, нелинейные упругие свойства, внутриглазное давление, математические модели
Короткий адрес: https://sciup.org/146282181
IDR: 146282181 | УДК: 531/534: | DOI: 10.15593/RZhBiomeh/2020.4.01
Текст научной статьи Оценка упругих характеристик глазного яблока по отклику энуклеированного глаза на введение заданных объемов жидкости
Любимов Григорий Александрович, д.ф.-м.н., профессор, г.н.с. Научно-исследовательского института механики, Москва результатов на живой глаз не вполне правомерен, поскольку ткани глаза претерпевают значительные посмертные изменения даже при максимально бережных условиях хранения. Тем не менее теоретические исследования, как правило, базируются именно на такого рода данных.
Однако есть и другое важнейшее обстоятельство, делающее формальный перенос на живой глаз полученных in vitro результатов затруднительным. Дело в том, что механические свойства тканей глаза очень индивидуальны. В экспериментах на живом глазу показано, что значения интегральных параметров, определяющих упругое поведение глаза, хотя и коррелируют с различными особенностями индивидуума (возраст, форма глазного яблока и т.д.), не могут быть заранее предсказаны для конкретного пациента [25]. Тем более невозможно заранее оценить всё множество параметров, характеризующих механические (или хотя бы упругие) свойства глазных тканей.
Эффективным оказывается иной подход: отказавшись от избыточной детализации, построить грубую математическую модель, параметры которой могут быть оценены в немногих тестах, выполнимых в клинике. По существу, именно по этому пути пошли исследования 30–60-х годов прошлого века, которые имели целью тарировку тонометров, т.е. создание методики определения физически достоверных характеристик (в первую очередь внутриглазного давления) по косвенным данным, получаемым врачом в результате тонометрии. Однако результаты этих исследований и разработанные на их основе рекомендации не были вполне корректными с физической точки зрения и позволяли в значительной степени произвольно интерпретировать клинические измерения. Их недостаточная информативность связана не только с тем, что они разрабатывались без участия профессионалов-механиков, но и с тем, что используемая (обычно неявно) механическая модель глаза была чрезмерно грубой: его упругие свойства характеризовалась единственной величиной – так называемой ригидностью. Этот параметр определялся по-разному в зависимости от используемого для его оценки испытания, а затем его значение использовалось для интерпретации результатов измерений, полученных при других условиях нагружения [7]. При этом, естественно, приходилось использовать не вполне корректные (и не всегда явные) допущения.
Нами была предложена методика [3], позволяющая сохранить при моделировании небольшое количество параметров, описывающих механические свойства роговицы и склеральной области. Основываясь на установленном ранее факте слабого сопротивления роговицы изгибу [2], мы предложили рассматривать роговицу как безмоментную двумерную поверхность, а склеральную область – как нульмерный элемент, характеризуемый объемом, зависящим от внутриглазного давления. В отличие от интегральных характеристик целого глаза, параметры, определяемые при таком подходе, раздельно отражают реальные механические свойства роговицы и склерального сегмента, что существенно как для диагностики, так и для оценок, имеющих значение при лечении, и для планирования операций. В частности, оказывается возможным определять в клинике внутриглазное давление, корректно учитывая поправки, вносимые индивидуальными механическими особенностями обследуемого глаза. Развиваемый нами подход позволяет по мере необходимости эффективно дополнять первоначальную модель, в которой роговица и склеральный сегмент полагались линейно-упругими, а роговица изотропной и однородной в тангенциальном направлении, учитывая различные усложняющие факторы, существенные в тех или иных ситуациях [4, 5].
Средние для здоровых глаз значения упругих характеристик, присутствующих в нашей модели, мы определили в [3], основываясь на клинических измерениях и предполагая упругое поведение роговицы и склеральной области линейным. Между тем клинические исследования показали, что нелинейность может оказаться существенной в тех случаях, когда в процессе механического воздействия на глаз (при тонометрии или инъекциях) давление в нем значительно увеличивается по сравнению с ненагруженным состоянием. Соответствующее обобщение модели роговицы, в котором нелинейное поведение характеризуется единственным параметром, было нами разработано в [8]. Эта модель была тестирована в сравнении с данными экспериментов по раздуванию изолированной роговицы давлением. Удалось оценить диапазон изменения параметра нелинейности для мертвой роговицы человека.
Ближе к ситуации, имеющей место в живом глазу, эксперименты по раздуванию давлением уже не роговицы, а целого энуклеированного глаза. Такие эксперименты, в немалом количестве выполнявшиеся в 30–60-е годы прошлого века [12, 22, 23, 27], демонстрируют заметную нелинейность кривой давление–объем, хотя и намного более слабую, чем обеспечиваемая нелинейностью упругих свойств изолированной роговицы нелинейность зависимости смещения ее апекса от давления. В предлагаемой работе развивается методика оценки параметров предложенной нами нелинейной модели на основании вышеупомянутых экспериментов, и результаты расчетов сопоставляются с данными для конкретных глаз, приводимыми в литературе. Показано, в частности, что в физиологически важном диапазоне давлений нелинейностью упругого поведения склеральной области можно пренебрегать. В какой степени полученные результаты могут быть применены к живому глазу, покажут дальнейшие исследования.
С истема уравнений и метод решения
В расчетах использовалась подробно описанная нами ранее система уравнений равновесия и геометрических соотношений для роговицы как двумерной безмоментной поверхности при геометрически малых деформациях (см., например, [3], (1.1)).
Определяющие соотношения для усилий T и T , действующих в роговице в меридиональном и перпендикулярном ему направлениях (главных двумерных напряжений), принимаем в соответствии с [8] в виде
T = A[ B (exp( B г, + C 82) - 1) + C (exp( B 82 + C 8,) - 1)] + T o, T 2 = A [ B (exp( B 82 + C 8!) - 1) + C (exp( B 8! + C s2) - 1)] + T ,
B = ^
C = ^- B
Здесь 8; и 82 - компоненты двумерного тензора деформации роговицы в направлениях главных осей (диагональные компоненты этого тензора равны нулю в силу постановки задачи); с; - безразмерный параметр нелинейности, а Ес ' и vc - упругие модули (модуль растяжения и коэффициент Пуассона) роговицы как двумерной, линейноупругой поверхности при нулевых деформациях (т.е. при Т = Т = То ). Постоянная величина Т о определяется формулой Т = pR / 2, где р0 - начальное давление, а Rc -радиус роговицы при этом давлении. Такое представление соответствует допущению, что при давлении p роговица имела форму сферического сегмента. Далее будем использовать формально введенный модуль растяжения материала роговицы Ec = Ec ' / 5С, где 5С = 0,5 мм. Для роговицы, имеющей стандартную толщину 0,5 мм, этот модуль совпадает со средним по толщине значением жесткости.
Граничные условия для ненагруженной извне роговицы – те же, что использовались нами ранее [4], с учетом представленной в [6] несколько иной формы для асимптотического условия в апексе, соответствующего допущению об ограниченности усилий. Второе условие в апексе – геометрическое и требует в этой точке нормальности представляющей роговицу поверхности к оси глаза. По-прежнему считается, что при решении уравнений, описывающих роговицу, условие закрепленности роговицы на границе со склерой можно ставить при начальном радиусе этой границы – допущение, обоснованное в [3]. Численное решение этих уравнений осуществлялось методом стрельбы с использованием схемы Рунге–Кутта четвертого порядка.
Моделирование целого глазного яблока должно учитывать как роговицу, так и склеральный объем. В [6] при моделировании тонометрии по Маклакову мы впервые в рамках нашего подхода использовали модель, соединяющую модель экспоненциально упругой роговицы [8] и представление склеральной области упругим элементом. В случае энуклеированного глаза, в отличие от живого, отсутствуют ткани, окружающие склеру, и, таким образом, склеральная жесткость E есть интегральная характеристика упругих свойств уже только самой склеральной оболочки.
Если представить склеру сферическим сегментом постоянной толщины δ , эта величина определяется формулой Es = Es * / д , где Es * - погонная жесткость склеры (аналогичная величине Ес ' для роговицы). Жесткость Es имеет теперь физический смысл средней по толщине жесткости материала склеры, пересчитанной на стандартную толщину δ , которая далее принимается равной 1 мм.
Однако само представление склеры сферическим сегментом – весьма произвольное допущение, особенно когда рассматриваются глаза с миопией или гиперметропией. Таким образом, параметр E здесь, как и в наших прежних работах (впервые в [3]) характеризует упругие свойства не материала склеры, а всей склеры как твердого тела. Это жесткость условной оболочки, имеющей форму сферического сегмента стандартных радиуса и толщины, откликающейся на приращение внутреннего давления тем же приращением объема, что и рассматриваемый склеральный сегмент. Только эта величина и может оцениваться в экспериментах, если нет дополнительных геометрических сведений. В частности, при тех же толщине оболочки и упругих свойствах материала модуль E , как правило, меньше для более объемной склеральной области, чем для менее объемной.
При исследовании нелинейно-упругого деформирования глазного яблока нельзя исключить нелинейного деформирования не только роговицы, но и склеры. Поэтому рассмотрим аналогичное (1) экспоненциально нелинейное обобщение ранее использовавшегося нами соотношения, связывающего приращения внутриглазного давления и склерального объема V :
A p = - [ехр( кА V s ) - 1]. (2) κ
Здесь κ – параметр нелинейности для склеральной области, Δ p = p - p , а Δ V = V - V , где V – начальный склеральный объем (при p = p ). Коэффициент L имеет смысл модуля объемного растяжения склеральной области при малых изменениях объема. В этом случае
A p = - A V s . (3)
Соотношение (3) описывает линейно-упругое поведение склерального сегмента и многократно использовалось нами ранее (см., например, [3, 4, 6]).
При представлении склеры равномерно растягивающимся сферическим сегментом (т.е. с сохранением сферичности) с оболочкой конечной постоянной толщины δ из однородного материала коэффициент L имеет следующий вид:
L= 2 E s 5 s
3(1 -Vs )VsRs ’ где ν – коэффициент Пуассона материала склеры, а под E понимается теперь начальная жесткость материала склеры (при p= p).
Исследуется связь приращений объема и давления для глазного яблока в целом. Приращение объема рассматривается как сумма приращений склерального объема Δ V и подроговичного объема Δ V , определяемого в результате решения рассмотренной выше краевой задачи для роговичного сегмента. Полученная в результате расчетов связь сравнивается далее с полученной в экспериментах.
П редварительные оценки
Во введении к работе [8] были выполнены оценки, позволившие заключить, что в широком диапазоне физиологически допустимых давлений деформации роговицы остаются геометрически малыми. С учетом полученной в той работе (и уточняемой ниже) оценки значений параметра нелинейности оказывается возможным еще более расширить интервал давлений, в которых условие малости деформаций роговицы заведомо остается в силе. В самом деле, среднее приращение Δσ = σ - σ тангенциального растягивающего напряжения σ в равномерно растягиваемой роговице, рассматриваемой как оболочка, имеющая форму сферического сегмента радиусом R и толщиной δ , при изменении давления на величину Δ p может быть оценено формулой [3]
Ac c = ( A pR c )/(2 5 c ). (5)
В отличие от линейно-упругой роговицы (рассмотренной при оценке, выполненной в [8]), связь Δσ с тангенциальной деформацией ε (в рассматриваемом случае деформация однородна, т.е. ε = ε = ε ) теперь нелинейна. Имеет место следующая зависимость, непосредственно вытекающая из формулы (12) в [8]:
E
Ac c = n c , (eXP( S£ c ) — D, (6)
? (1 — V c )
где E – жесткость роговицы при начальном давлении p , соответствующем начальному напряжению cc0 = p0Rc / (25c) .
Сравнение с данными экспериментов по растяжению изолированной роговицы дало возможность оценить значение параметра нелинейности роговицы ς в диапазоне 60–100 [8]. При этом максимально вероятным оказался еще более узкий диапазон g = 60...80.
Коэффициент Пуассона для роговицы как поверхности близок к 0,5 в силу того, что она как трехмерный материал почти несжимаема. Функция в правой части (6) возрастает по Ec, sc и (при ac > 0) по ^. Даже при очень малой начальной жесткости роговицы Ес = 0,1 МПа и параметре нелинейности g = 40 деформация г = 0,1, которая еще может считаться геометрически малой, достигается при нереальном для глаза (даже в экспериментах in vitro) перепаде давлений Δp , превосходящем 1000 мм рт. ст. Значение параметра нелинейности взято ниже оцененного в [8] диапазона, поскольку g = 40 оказывается нижней границей диапазона g, оцененного по рассмотренным далее экспериментам, что лишь еще более занижает оценку. Использованы стандартные геометрические параметры роговицы Rc = 8 мм и 5С = 0,5 мм. Таким образом, о нарушении условия геометрической малости деформаций роговицы не может быть и речи. Заметим, что даже в случае линейно-упругой (жесткость постоянна) и очень мягкой роговицы деформация г ~ 0,1 достигается весьма высоким приращением давления: Др ~ 20 мм рт. ст. при Ес ~ 0,1 МПа и порядка 40 мм рт. ст. при Ес ~ 0,2 МПа (приведенные значения приращения давления приблизительно вдвое выше, чем более грубая оценка, данная в [8]).
Тем не менее упругое поведение роговицы (по крайней мере в экспериментах in vitro ) заметно нелинейно (физическая нелинейность), что и учтено моделью, предложенной в [8], на базе которой оценивался параметр нелинейности ς .
Для склеральной области, которая в рамках развиваемого подхода моделируется нульмерным объектом, вопрос о геометрической нелинейности не стоит, однако остается открытым вопрос о физической нелинейности: можно ли пользоваться линейной связью между давлением и приращением ее объема? В [6] проведено оценочное сравнение (в рамках линейной модели) тангенциальных деформаций склеры и роговицы при одном и том же давлении с использованием формулы (5) для роговицы и аналогичной оценочной формулы для напряжения в склере (последняя, как и роговица, приближенно считается сферическим сегментом):
Да , = ( Д р R s )/(2 5 s ). (7)
При средних значениях жесткостей роговицы и склеры Ес = 0,3 МПа и Es = 10 МПа, vc ~ v^ ~ 0,5 и стандартных значениях геометрических параметров (для склеры радиус соответствующего сегмента и толщина равны соответственно Rs = 12 мм и ds = 1 мм) отношение гс / г имеет порядок 0,5 х 102, т.е. деформация роговицы более чем на порядок превосходит деформацию склеры. Это прежде всего означает, что в физиологически значимых процессах деформации склеры остаются геометрически малыми. Кроме того, можно ожидать, что и физическая нелинейность будет проявляться в деформациях роговицы при намного меньших давлениях, чем в деформациях склеры. Рассмотрим этот вопрос более детально.
Преобразуем, используя (4) и (7), нелинейное соотношение (2), связывающее приращения склерального объема и давления, в зависимость тангенциального напряжения в склере от тангенциальной деформации:
E
Да s = пs . (exp( g s s s ) - 1), (8) g s (1 -v s )
где ^ s = 3 V к имеет смысл параметра нелинейности материала склеры. При получении выражения (8) учтено, что относительное приращение склерального объема можно представить в виде Д V / KOs = 3s,,, что правомерно в силу геометрической малости деформаций склеры. Для приращения давления из соотношений (5)–(8) имеем
2 E 8 2 E 8
A P = Л c XD ^xP^ 8 c ) - ^ A P = n lD(eXP( S s 8 s ) - 1) g (1 -V c ) R c g s (1 -V s ) R s
Предположим, что параметры нелинейности материала для склеры и роговицы одного порядка (g5 ~ g ). Обозначим через A pCE и A ps Е такие приращения давления, при которых одна и та же деформация 8 достигается соответственно в роговице и склере. Тогда в силу (9) отношение этих приращений имеет порядок
Ар РЬЕ pc 8 s c c
----- ~ --------. A P s 8 R c 8 s E s
Одна и та же деформация (и, соответственно тот же уровень нелинейности) достигается в склере при порядке приращений давлений над начальным уровнем в 50 раз выше. Таким образом, учитывать нелинейность упругого деформирования склеры нужно лишь при столь высоких давлениях, при которых роговица из-за увеличения жесткости уже стала в деформировании значительно отставать от склеры. Разумеется, утверждение, что g5 ~ g , предположительно и нуждается в экспериментальной проверке.
При расчетах геометрические параметры роговицы и склеры выбирались соответствующими «среднему» глазу [3], коэффициент Пуассона для обоих сегментов vc =vs = 0,45. Во всех последующих расчетах в соответствии с выполненной выше оценкой предполагалось, что упругость склерального сегмента линейна и, таким образом, для склеры использовалось соотношение (3). Как будет показано ниже, это допущение хорошо соответствует данным измерений, и, таким образом, необходимости использовать нелинейную зависимость (2) в самом деле не возникает. Жесткости склеры и роговицы Es и Ec и параметр нелинейности роговицы g подбирались в соответствии с экспериментальными данными для каждого конкретного энуклеированного глаза.
Р езультаты расчетов и их сопоставление с экспериментом
При однородном растяжении сферического сегмента, представляющего роговицу, давлением можно ввести жесткость роговицы как функцию деформации. Из формулы (6) следует следующее выражение для этой жесткости:
E c ( 8 c ) = d ^=T E c - exP( g8 c )■ d 8, 1 — v„
Здесь и далее обозначение E (без указания аргумента) сохранено за начальной жесткостью: Ec = Ec (0). Таким образом, жесткость роговицы экспоненциально возрастает с ростом 8С . Что касается деформации, то она, хотя формально (в рамках модели), растет неограниченно с ростом напряжения, но ее рост постепенно замедляется по логарифмическому закону. Из первой формулы (9)
1i (i
8 c = - ln 1 + g I
g (i -v c ) R c 2 E c 8 c
Л p ■
По аналогичному закону растет (с учетом геометрической малости деформаций) и приращение подроговичного объема Л Vc = 3sc. В рассматриваемой задаче о совместном деформировании подроговичного и склерального объемов при одном и том же давлении в обеих областях деформация роговицы неоднородна и формулы (11), (12) не выполняются. Однако они указывают на то, что изменение подроговичного объема может быть весьма существенно при небольших давлениях, тогда как при больших давлениях его вклад в дальнейшее изменение полного внутриглазного объема становится существенно меньшим, чем вклад склерального объема. Последнее связано с тем, что склеральный объем возрастает (в рамках принятой упрощенной модели) с ростом давления равномерно: отношение приращения склерального объема к приращению давления от давления не зависит. Это отношение в соответствии с формулой (3) постоянно: AVs / Ap = L- . Таким образом, в приращении полного объема с ростом давления всё более заметной будет становиться доля линейной (склеральной) составляющей, и зависимость объема от давления должна приближаться к линейной.
а
б
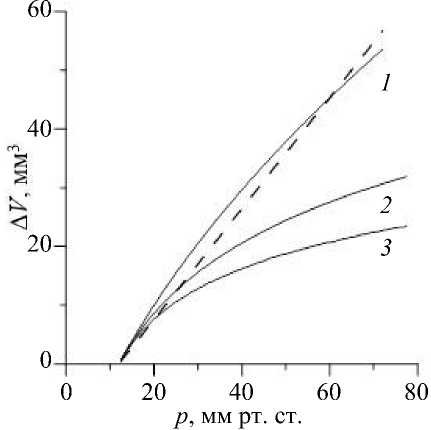
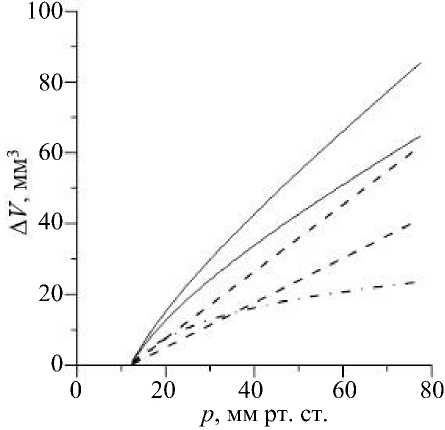
Рис. 1. Вклад подроговичного и склерального объемов в изменение внутриглазного объема с изменением внутриглазного давления при разных значениях коэффициента нелинейности роговицы ( а ) и разных значениях жесткости склеры ( б) ; p о = 12 мм рт. ст.: а - пунктир - склеральный объем ( E s = 0,3 МПа), сплошные линии - подроговичный объем ( E c = 0,3 МПа, ^ = 1 ( 1 ), 30 ( 2 ), 60 ( 3 )); б – сплошные линии – полный внутриглазной объем, пунктир – склеральный объем (в обоих случаях E s = 10 МПа для верхних кривых и 15 МПа для нижних), штрих-пунктир - подроговичный объем ( E c = 0,3 МПа, ^ = 60)
На рис. 1 показаны результаты численного расчета, подтверждающие справедливость такого ожидания. На рис. 1, а изображены зависимости от давления приращений склерального объема при нормальной склеральной жесткости Es = 10 МПа и подроговичного объема при также нормальной жесткости роговицы Ec = 0,3 МПа и трех значениях параметра нелинейности ^ = 1 (практически линейное поведение [8]), 30 и 60. Естественно, и при линейном поведении роговицы как материальной поверхности зависимость приращения подроговичного объема от давления слабо нелинейна из-за неоднородности деформации роговицы. Из графика видно, что при линейно-упругой роговице приращение полного объема распределено между двумя сегментами почти поровну. Зависимость этого распределения от давления незначительна. Такое распределение имеет место и при нелинейно-упругой роговице, пока давление возрастает не слишком существенно. Однако чем более увеличивается давление, тем медленнее растет подроговичный объем. Скорость увеличения склерального объема остается постоянной - dVs / dp = 0,944 мм3/мм рт. ст., а скорость изменения подроговичного объема dVc / dp принимает для д = 30 при p = 12, 40 и 70 мм рт. ст. значения 1,28, 0,49 и 0,27 мм3/мм рт. ст. соответственно. Для д = 60 падение dVc / dp еще заметнее: при тех же давлениях dVc / dp = 1,23, 0,22 и 0,11 мм3/мм рт. ст.
Относительный вклад изменения подроговичного объема в изменение общего внутриглазного объема тем больше, чем меньше параметры Ec и д и чем выше жесткость склеры Es . Как видно из сравнения приведенных выше значений dVs / dp и dVc / dp, с возрастанием давления при значениях параметра нелинейности 30 и более приращение склерального объема становится определяющим. При д = 60 и p = 70 мм рт. ст. оно уже на порядок превосходит вклад подроговичного объема.
На рис. 1, б видно, что кривые А V ( p ) с ростом давления практически выходят на прямые линии, наклон которых не слишком значительно отличается от наклона прямых А V ( p ). Естественно, на прямые с ростом объема будут выходить и кривые p ( А V ). Характеристика жесткости глазного яблока в целом при объемном растяжении – модуль объемного растяжения (объемная жесткость) E = dp / dV = ( dV / dp ) - 1 [3]. Эта величина равна наклону кривых p ( А V ) , обратна наклону кривых A V ( p ) и зависит от давления. Модуль E существенно меняется на начальном отрезке, а затем возрастает слабо. Для Es = 10 МПа при изменении Ap от 0 до 30 мм рт. ст. E возрастает от 0,5 до 0,75 мм рт. ст./мм3, а при дальнейшем росте Ap до 60 мм рт. ст. лишь до 0,83 мм рт. ст./мм3. Аналогично для Es = 15 МПа при возрастании давления от 0 до 30 мм рт. ст. происходит рост модуля E почти вдвое – от 0,6 до 1,1 мм рт. ст./мм3, тогда как на отрезке той же длины от 30 до 60 мм рт. ст. он увеличивается меньше чем на 20% – до 1,3 мм рт. ст./мм3. Сакральная для офтальмологов ригидность по Фриденвальду [19] вычисляется как показатель экспоненты при приближении экспоненциальной зависимостью непосредственно интегральной кривой p ( А V ) (зависимость А V ( p ) в этом случае - логарифмическая). При аппроксимации экспонентой на отрезке 12–60 мм рт. ст. константа Фриденвальда для верхней кривой ( Es = 10 МПа) равна 0,023 мм-3, а для нижней ( Es = 15 МПа) -0,031 мм–3. Первое из приведенных значений, рассчитанное для средних по нашим оценкам значений упругих констант Es = 10 МПа и Ec = 0,3 МПа, практически совпадает (лишь на 7% больше) со средним значением этой константы для многих глаз 0,0215 мм–3, полученным Фриденвальдом [19].
По наклону кривых А V ( p ) при достаточно больших давлениях можно на основании формул (3) и (4) в первом приближении непосредственно оценить склеральную жесткость E :
E = kdp , k = 3(1 -V 5 ) V ° sRs = 0,694 x 105мм 3 . (13) s dV ^25,
Значение коэффициента k в (13) соответствует принятым стандартным значениям параметров склеры (кроме жесткости) в предположении, что объем склеральной области измеряется в мм3, а давление и жесткость – в одних и тех же единицах. Если эти величины традиционно измерять в мм рт. ст. и МПа соответственно, необходимо вводить коэффициент пересчета.
Далее проводится сравнение с данными экспериментов по раздуванию давлением энуклеированных глаз. Такого рода исследований выполнено немало, особенно много в 30–60-х годах XX века [12, 22, 23, 27]. Их результаты тогда использовались (хотя и не вполне корректно) для тарировки статических тонометров [19, 20, 24]. Вследствие практической несжимаемости вводимой жидкости (водного раствора) и обеспечиваемого в опыте отсутствия ее оттока изменение внутриглазного объема в старых экспериментах по раздуванию энуклеированного глаза оценивалась по объемам поступающего во внутриглазное пространство раствора. Такого рода опыты иногда проводятся и в настоящее время [16]. Некоторые исследователи [10] используют современные оптические технологии, позволяющие измерять уже не объем вводимой жидкости, а изменение кривизны сегментов (роговичного и склерального) деформированного давлением глазного яблока. Однако выполняемая на основе таких измерений оценка параметров упругости не представляется слишком надежной. Дело в том, что из-за сложной структуры и достаточно большой толщины роговицы и склеры изменение кривизны их внешних поверхностей при малых (сравнимых с толщиной или меньших) деформациях может в недостаточной степени отражать деформацию этих сегментов, осредненную по толщине.
Отчетливая нелинейность зависимости А V ( р ) делает эту кривую достаточно информативной, чтобы оценить все три основных параметра, присутствующих в нашей модели. Мы будем проводить сравнение с кривыми, содержащимися в публикациях [22, 23], где приведены данные для конкретных глаз человека (без осреднения по многим глазам) в широком диапазоне давлений и с достаточным количеством экспериментальных точек для каждого глаза. При сравнении теоретических и экспериментальных кривых последние приводились к принятому в настоящей работе началу отсчета: A V = 0 при р0 = 12 мм рт. ст.
Вышеупомянутое спрямление кривых А V ( р ) при больших давлениях в самом деле наблюдается в эксперименте. Это позволило принять простой алгоритм первоначальной оценки упругих характеристик. Сначала по наклону экспериментальных кривых при максимальных в опыте давлениях оценивается склеральная жесткость E в соответствии с соотношением (13). Затем по поведению кривой вблизи отсчетного давления p , выбранного равным 12 мм рт. ст., подбирается начальная жесткость роговицы E . Это возможно сделать, поскольку при давлениях, близких к р 0, нелинейность практически не проявляется и деформация роговицы определяется ее начальной жесткостью при р = р 0. Завершающий этап - подбор значения параметра нелинейности роговицы g , наилучшим образом соответствующего форме экспериментальной кривой. Поскольку все сформулированные упрощения не просто приближенные, но и весьма грубые, при практической обработке экспериментальных кривых значения упругих параметров далее варьировались вблизи оцененных первоначально значений с тем, чтобы добиться минимального отклонения теоретических зависимостей от экспериментальных.
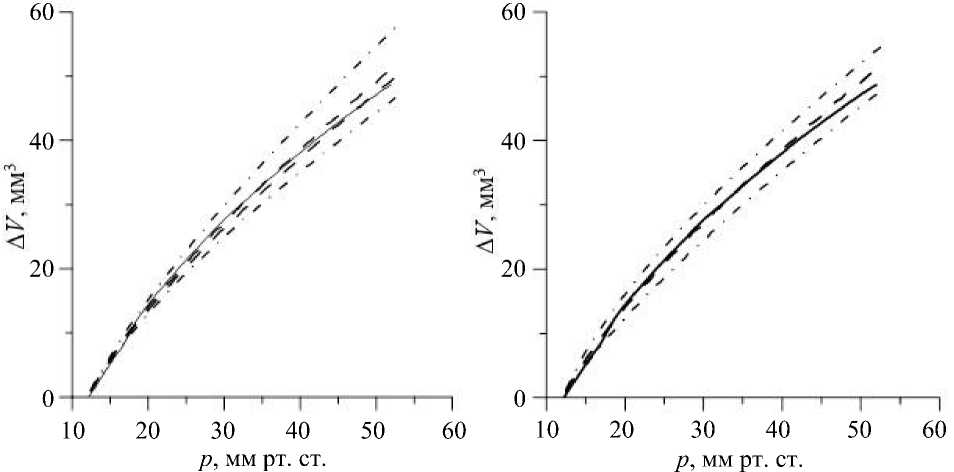
Рассмотрим сначала экспериментальную кривую для конкретного глаза, приведенную в работе [23] (рис. 4 в этой работе). Заметим, что, хотя давление в экспериментах, представленных в [23], повышалось до значений, значительно превышавших физиологические, вводимые объемы жидкости оставались все же значительно меньше, чем максимальные объемы, вводимые в настоящее время при инъекциях. Рассматриваемая кривая, как видно из рис. 2, хорошо приближается различными теоретическими кривыми. Качество приближения зависит от интервала, на котором мы стремимся достичь наилучшего результата. Кривая с Es = 12 МПа, Ec = 0,3 МПа и g = 70 с высокой точностью описывает эксперимент в достаточно широком интервале давлений.
б
а
Рис. 2. Сравнение экспериментальной [23] (сплошная линия) и расчетных кривых при E c = 0,3 МПа ( а ) и E s = 12 МПа ( б); а - пунктирные кривые - E s = 12 МПа, д = 60 (верхняя) и д = 70 (нижняя), штрихпунктирные кривые - д = 60,
E s = 10 МПа (верхняя) и E s = 14 МПа (нижняя); б - g = 60, пунктирная кривая - E c = 0,3 МПа, штрихпунктирные кривые - E c = 0,2 МПа (верхняя) и E c = 0,4 МПа (нижняя)
Если следить за изменением объема лишь при давлениях до 40 МПа (этот интервал перекрывает значения, как правило, наблюдаемые в глазу), то видно, что верхняя пунктирная кривая ( g = 60) лучше повторяет нелинейную форму экспериментальной кривой. Но если поставить задачу воспроизведения всего экспериментального интервала давлений (до 52 мм рт. ст.), лучше подходит кривая с g = 70. Впрочем, отклонения теоретических кривых от экспериментальной в обоих случаях ничтожны (не более 3%).
Заметим, что отклонение экспериментальной кривой вниз от теоретической для больших давлений может быть связано с тем, что при таких давлениях начинает проявляться нелинейность упругого поведения склеры. Описание данных эксперимента посредством увеличения g может в этом случае означать попытку объяснения наблюдаемых фактов завышенной нелинейностью роговицы, тогда как в действительности они связаны уже с нелинейностью склеры. Если бы интервал исследованных давлений был длиннее, стал бы возможен мотивированный выбор между двумя объяснениями (см. ниже).
Следует также иметь в виду, что представление уравнения состояния роговицы в экспоненциальной форме, возможно, лишь грубо отражает ее нелинейные свойства. Имеются данные (хотя их и немного), что жесткость роговицы может почти скачкообразно меняться при достижении определенного уровня растягивающих напряжений [9]. В этом случае возрастание подходящего параметра нелинейности g при расширении интервала давлений, в котором он подбирается, представляется естественным. Практического значения столь точное рассмотрение не имеет.
Отклонения E от выбранного значения на 2 МПа (штрихпунктирные кривые на рис 2, а ) и E на 0,1 МПа (штрихпунктирные кривые на рис 2, б ) приводят к заметным отклонениям от экспериментальных данных, тогда как изменение g даже на 10 сказывается на форме кривой незначительно. О пунктирных кривых на рис 2, а с параметром нелинейности g , различающимся на 10, сказано выше, а, например, при Es = 12 МПа и Ес = 0,4 МПа кривые с g = 60 и 70 совпадают с графической точностью (нижняя штрихпунктирная кривая). В конечном счете можно заключить, что по данным эксперимента параметры модели определяются с точностью не более чем 1 МПа для Es , 0,05 МПа для Ес и 10 для g . Так, например, расчетная кривая с Es = 11 МПа, Ес = 0,3 МПа и g = 50 приближает при давлениях меньше 40 мм рт. ст. экспериментальную практически с той же точностью, что и подобранная выше для этого интервала кривая с Es = 12 МПа, Ес = 0,3 МПа и g = 60.
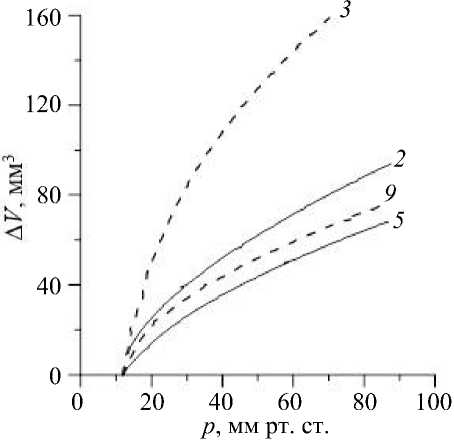
Рис. 3. Результаты экспериментов по раздуванию энуклеированных глаз давлением [22]. Номера кривых совпадают с номерами глаз в этой работе
В [22] (см. рис. 2 в этой работе) приведены раздельно по каждому глазу результаты эксперимента, в котором обследовались 9 энуклеированных глаз. С учетом преобразования к используемым нами отсчетным данным эти результаты представлены на рис. 3. Все зависимости объем–давление (кроме зависимости для глаза 3 ) демонстрируют близкое поведение и расположены между кривыми 2 и 5 (для примера показана кривая для глаза 9 ).
На рис. 4 представлены оценки параметров глазной оболочки глаз 2 и 5. В экспериментах, представленных в [22], давление повышалось до 80 мм рт. ст. и более. При этом объем вводимой жидкости приближался к 100 мм3, а иногда его и превышал. Объемы, вводимые в глаз при интравитреальных инъекциях, как правило, такого порядка или меньше. Оказалось, что наилучшее совпадение с приведенными в этой работе кривыми, если ограничиваться областью до 60 мм рт. ст., достигается, если оценивать Es по наклону кривой в области p = 50...60 мм рт. ст. При более высоких давлениях теоретические кривые, наилучшим образом подходящие для этого интервала, начинают заметно уходить вверх (что видно на рис. 4), т.е. дают завышенные значения объема. Такое поведение с наибольшей вероятностью может быть объяснено тем, что при больших давлениях начинает проявляться нелинейность
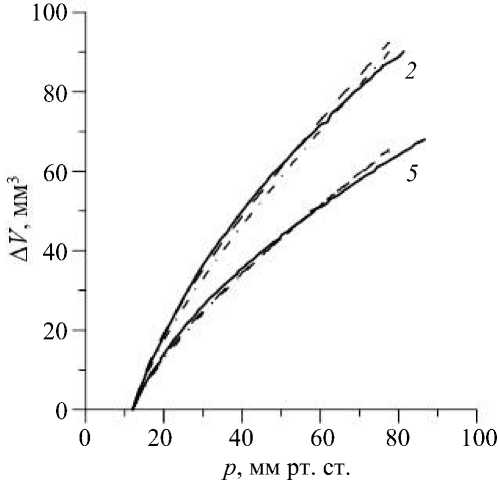
Рис. 4. Сравнение экспериментальных [22] (глаза 2 и 5) и расчетных кривых. Сплошные кривые – результаты экспериментов; пунктирные и штрихпунктирные – расчетные кривые с параметрами, значения которых приведены в тексте упругого поведения склеры: рост ее жесткости становится заметным. Нелинейные свойства склеры, таким образом, начинают проявляться при приращениях давления над начальным уровнем намного больших, чем те, при которых становятся существенными нелинейные свойства роговицы, что находится в согласии с нашими предварительными оценками. Для учета нелинейной упругости склерального сегмента несложно воспользоваться нелинейным соотношением (2), однако малость отклонений экспериментальных кривых объем–давление от результатов расчетов с линейной склерой даже при наибольших давлениях из исследованного диапазона (не более 3%) делает такое обобщение практически нецелесообразным.
Для экспериментальной кривой 5 наилучшее приближение в указанном интервале достигается при Es = 15 МПа, Ес = 0,3 МПа и ^ = 60 (пунктир). Отметим, что кривая, для которой Es = 15 МПа, Ес = 0,25 МПа и ^ = 70 (штрихпунктир) подходит не хуже, что указывает на вышеупомянутую ограниченную точность оценки констант, даже если предположить, что измерения проводились с высокой точностью.
Оценка параметров глаза 2 дает следующий набор значений, с высокой точностью дающий совпадение с экспериментальными кривыми: Es = 10 МПа, Ес = 0,15 МПа, д = 60 (пунктир). Набор Es = 10 МПа, Ес = 0,20 МПа, д = 50 (штрихпунктир) дает не худшее совпадение, что находится в согласии с упомянутой выше точностью оценки. Из приведенных оценок видно, что оба компонента глаза 5 жестче соответствующих компонентов глаза 2 . С большой вероятностью у него больше и параметр нелинейности. Значения жесткостей роговицы и склеры и коэффициента нелинейности исследованных в [22] глаз (кроме глаза 3 ) находятся в диапазоне
Es = 10...15 МПа, Ec = 0,1...0,3 МПа, g = 40...70. В рассмотренном выше эксперименте из работы [23] оцененные значения Es и д находятся в том же диапазоне, а чтобы включить возможные значения E , оцениваемые по данным этого эксперимента, диапазон значений этой величины нужно несколько расширить: Ес = 0,1...0,4 МПа. Исключением оказывается глаз 3 из [22], параметры жесткости которого оказались значительно ниже остальных - Es = 6 МПа, Ес = 0,02 МПа при весьма низком значении также и параметра нелинейности g = 30 . Действительно ли этот глаз обладал аномальными механическими свойствами или же были нарушены условия эксперимента или хранения, естественно, сейчас сказать невозможно.
О бсуждение
Разработанная нами малопараметрическая модель упругого поведения глазного яблока, учитывающая нелинейную упругость роговицы, позволила эффективно описать классические эксперименты по раздуванию давлением энуклеированного глаза и оценить на их основе параметры модели: эффективные жесткости склерального и роговичного сегментов и параметр нелинейности роговицы.
Оказалось, что в диапазоне давлений, которые может испытывать живой глаз человека (в том числе при патологиях, статической тонометрии, инъекциях лекарственных препаратов), нелинейность экспериментальной зависимости объем– давление практически определяется нелинейностью упругого поведения роговицы. Влияние нелинейной упругости склерального сегмента обнаруживается лишь при очень высоких давлениях, которые в живом глазу достигаются разве что при наиболее объемных внутриглазных инъекциях. Да и то это влияние столь невелико, что при оценочных расчетах им можно спокойно пренебрегать.
Несмотря на существенную нелинейность упругого поведения роговицы, практическая линейность упругого отклика склеральной области сильно сглаживает нелинейность кривой объем–давление для глазного яблока в целом. Рост его объемной жесткости с давлением заметен лишь при умеренных давлениях (до 30 мм рт. ст.) При более высоких давлениях растяжение полного объема выходит на новый, близкий к линейному, закон с существенно большей объемной жесткостью. Это связано с тем, что с возрастанием давления доля приращения роговичного объема уменьшается и при достаточно больших давлениях становится практически пренебрежимой в сравнении с приращением склерального объема. Давление, при котором происходит выход на такой режим, тем выше, чем мягче роговица и ниже параметр нелинейности.
Оцененные при сравнении с экспериментом значения жесткостей роговицы и склеры Es = 10...15 МПа, Ес = 0,1...0,4 МПа большинства глаз оказались близки к средним значениям Es = 10 МПа и Ec = 0,3 МПа, полученным нами ранее [3] для живых неглаукомных глаз. Эти значения были определены в результате расчетов, базировавшихся на совместном учете результатов двух серий опытов: прямых измерений роста давления в передней камере в ответ на введение жидкости [25] и данных эластотонометрии [1]. Тенденция исследованных энуклеированных глаз к несколько большей склеральной жесткости, возможно, связана с посмертным изменением ткани, однако утверждать это с достоверностью, конечно, невозможно.
Значения параметра нелинейности g = 40...70 оказались близки (хотя в среднем и несколько ниже) к тому основному диапазону g = 60...80, который мы определили по данным экспериментов с целой изолированной роговицей [8]. Что касается жесткостей роговицы, оцененных нами в [8] на основе тех же экспериментов, то они оказались заметно выше наших оценок как для живого глаза, так и представленных в настоящей работе по данным для целого энуклеированного глазного яблока. Это расхождение может быть связано с особенностями организации опытов с изолированной роговицей, условия которых далеки от ситуации в целом глазу, как живом, так и энуклеированном.
З аключение
Выполненное сравнение расчетов, базирующихся на нашей модели, с данными экспериментов по раздуванию энуклеированного глаза давлением в очередной раз показало ее эффективность. Оно позволило оценить параметры модели для конкретных целых энуклеированных глаз, причем удалось достигнуть высокой точности совпадения теории с экспериментом. Полученные оценки жесткостей роговичного и склерального сегментов оказались близки к средним значениям, ранее оцененным нами на основании непрямых опытов in vivo . Тем не менее для конкретных глаз эти жесткости могут значительно различаться, что лишний раз указывает на необходимость учета индивидуальных упругих характеристик при расчетах, в частности при интерпретации данных тонометрии. Следует, впрочем, иметь в виду, что исследованные в эксперименте энуклеированные глаза различались возрастом и патологией индивидуума, от которого были взяты, а также длительностью посмертного хранения. Значения параметра нелинейности, полученные на основании экспериментов с целым энуклеированным глазом, лежат в диапазоне, пересекающемся с оцененным ранее по данным опытов с изолированной роговицей, однако в среднем несколько ниже.
На основании проведенного исследования удалось сделать ряд качественных выводов. Во-первых, нелинейность упругого поведения глазного яблока при раздувании (по крайней мере до давлений порядка 60 мм рт. ст.) определяется практически исключительно нелинейной упругостью роговичного сегмента. Во-вторых, при достаточно больших давлениях растяжение глаза в целом становится близким к линейному и определяется уже в основном растяжимостью склеры, нелинейностью упругого поведения которой при в исследованном диапазоне давлений практически можно пренебречь.
Близость оценок, сделанных на основании нашей модели для жесткостей живого и энуклеированного глаза, как указывает на адекватность самой модели, так и дает довод в пользу правомерности перенесения полученных на мертвом глазу данных на живой глаз, когда расчеты выполняются для «среднего» глаза. Разумеется, при работе с конкретным глазом в клинике, в частности при выполнении клинических измерительных процедур, необходимо знание индивидуальных механических параметров, которые должны определяться непосредственно в результате разумно организованных неинвазивных измерений.
Что касается степени нелинейности упругого поведения живого глаза, то этот вопрос на сегодняшний день открыт: имеются не слишком многочисленные данные, свидетельствующие в пользу его как существенно нелинейного, так и близкого к линейному отклика на изменение давления [15, 25, 29]. Прямые измерения зависимости давление–объем in vivo здесь не слишком полезны. Во-первых, они выполняются лишь в исключительных случаях и не могут включаться в процедуру клинического обследования. Во-вторых, точность таких измерений невелика, и даже просто убедительно разглядеть нелинейность (которая не слишком значительна), как правило, не удается. Тем не менее такие опыты дают возможность оценить объемную жесткость глазного яблока в целом, которая оказалась лежащей в диапазоне значений, полученных для энуклеированного глаза, и сильно вариабельной для разных испытуемых. Именно данные этих измерений, как упоминалось выше, мы использовали для оценки средних жесткостей роговицы и склеральной области [3]. Что касается оценки в клинике упругих параметров индивидуального глаза, включая степень нелинейности упругого отклика роговицы, то она должна выполняться посредством неинвазивного нагружения его различными тонометрами. Такая оценка необходима для корректного определения внутриглазного давления и имеет самостоятельную диагностическую ценность. Разрабатываемый нами подход дает возможность решения этой задачи.
Определяющая нелинейное поведение глазного яблока нелинейность роговицы наиболее заметна при низких давлениях – тем заметнее, чем эти давления ниже. Необходимость учета нелинейных эффектов при решении конкретных задач возрастает как при попадании низких давлений в реализуемый в рассматриваемом процессе диапазон давлений, так и при расширении этого диапазона. В последнем случае приходится учитывать переход в одном опыте от мягкой роговицы к жесткой. Эти общие соображения для случая тонометрии по Маклакову подтверждены в нашей работе [6]: поправки из-за нелинейности упругих свойств роговицы становятся тем существеннее, чем меньше истинное давление и больше вес тонометра, с увеличением которого возрастает тонометрическая разность, т.е. разность между тонометрическим и истинным давлениями.
Б лагодарности
Работа выполнена в рамках Госпрограммы АААА-А19-119012990119-3.
Список литературы Оценка упругих характеристик глазного яблока по отклику энуклеированного глаза на введение заданных объемов жидкости
- Аветисов С.Э., Бубнова И.А., Антонов А.А. Диагностические возможности эластотонометрии // Глаукома: реальность и перспективы: сб. науч. ст. / под ред. С.Э. Аветисова; НИИ глазных болезней РАМН. - М.,2008. - Ч. 2. - С. 81-85.
- Бауэр С.М., Любимов Г.А., Товстик П.Е. Математическое моделирование метода Маклакова измерения внутриглазного давления // Изв. РАН. Механика жидкости и газа. - 2005. - № 1. -С. 24-39.
- Моисеева И.Н., Штейн А.А. Анализ зависимости давление-объем для глазного яблока, нагруженного плоским штампом, на основе двухсегментной упругой модели // Изв. РАН. Механика жидкости и газа. - 2011. - № 5. - С. 3-15.
- Моисеева И.Н., Штейн А.А. Влияние пространственной неоднородности роговицы на деформационные свойства глазного яблока и результаты аппланационной тонометрии по Маклакову // Биофизика. - 2017. - Т. 62, № 6. - С. 1193-1203.
- Моисеева И. Н., Штейн А. А. Математическое моделирование деформирования роговицы глаза приложенным извне давлением // Российский журнал биомеханики. - 2019. - Т. 23, № 4. -С. 511-525.
- Моисеева И.Н., Штейн А.А. Математическое моделирование аппланационного нагружения глазного яблока с учетом нелинейности упругих свойств роговицы // Российский журнал биомеханики. -2020. - Т. 24, № 3. - С. 272-281.
- Штейн А.А. О понятии ригидности глаза // IV Российский общенациональный офтальмологический форум: сб. тр. науч.-практ. конф. с междунар. уч., Москва 5-7 октября 2011 г. / под ред. В.В. Нероева; Московский научно-исследовательский институт глазных болезней им. Гельмгольца Минздравсоцразвития России. - М., 2011. - Т. 2. - С. 257-261.
- Штейн А.А., Моисеева И.Н., Любимов Г.А. Математическая модель роговицы глаза с учетом экспоненциальной нелинейности ее упругих свойств при условии геометрической малости деформаций // Российский журнал биомеханики. - 2019. - Т. 23, № 3. - С. 375-390.
- Anderson K., El-Sheikh A., Newson T. Application of structural analysis to the mechanical behaviour of the cornea // Journal of the Royal Society Interface. - 2004. - Vol. 1, no. 1. - P. 3-15.
- Asejczyk-Widlicka M., Pierscionek B.K. The elasticity and rigidity of the outer coats of the eye // The British Journal of Ophthalmology. - 2008. - Vol. 92, no. 10. - P. 1415-1418.
- Bryant M.R., McDonnell P.J. Constitutive laws for biomechanical modeling of refractive surgery // The Journal of Biomechanical Engineering. - 1996. - Vol. 118, no. 4. - P. 473-481.
- Clark J.H. A method for measuring elasticity in vivo and results obtained on the eyeball at different intraocular pressures // The American Journal of Physiology. - 1932. - Vol. 101. - P. 474-481.
- Corneal Biomechanics and Refractive Surgery. Ed. F.A. Guarnieri. - Berlin: Springer, etc., 2015. - 146 p.
- Coudrillier B., Pijanka J., Jefferys J., Sorensen T., Quigley H.A., Boote C., Nguyen T.D. Collagen structure and mechanical properties of the human sclera: analysis for the effects of age // The Journal of Biomechanical Engineering. - 2015. - Vol. 137, no. 4. - 041006.
- Detorakis E.T., Pallikaris I.G. Ocular rigidity: biomechanical role, in vivo measurements and clinical significance // Clinical and Experimental Ophthalmology. - 2013. - Vol. 41, no. 1. - P. 73-81.
- Dyk D.W., Miller K.M. Mechanical model of human eye compliance for volumetric occlusion // Journal of Cataract & Refractive Surgery. - 2018. - Vol. 44. - P. 231-236.
- Elsheikh A., Alhasso D., Rama P. Biomechanical properties of human and porcine corneas // Experimental Eye Research. - 2008. - Vol. 86. - P. 783-790.
- Fernandez D.C., Niazy A.M., Kurtz R.M., Djotyan G.P., Juhasz T. Finite element analysis applied to cornea reshaping // The Journal of Biomedical Optics. - 2005. - Vol. 10, no. 6. - 064018. - P. 1-11.
- Friedenwald J.S. Contribution to the theory and practice of tonometry // The American Journal of Ophthalmology. - 1937. - Vol. 20, no. 10. - P. 985-1024.
- Friedenwald J.S. Standartization of tonometers: decennial report by the committee on standartization of tonometers. - American Academy of Ophthalmology and Otolaryngology, 1954. - 177 p.
- Hjortdal J.0. Regional elastic performance of the human cornea // Journal of Biomechanics. - 1996. -Vol. 29, no. 7. - P. 931-942.
- Macri F.J., Wanko T., Grimes P.A. The elastic properties of the human eye // AMA Archives of Ophthalmology. - 1958. - Vol. 60, no. 6. - P. 1021-1026.
- McBain E.H. Tonometer calibration. II. Ocular rigidity // AMA Archives of Ophthalmology. - 1958. -Vol. 60. - P. 1080-1091.
- Moses R.A. Theory of the Schi0tz tonometer and its empirical calibration // Transactions of the American Ophthalmological Society. - 1971. - Vol. 69. - P. 494-562.
- Pallikaris I.G., Kymionis G.D., Ginis H.S., Kounis G.A., Tsilimbaris M.K. Ocular rigidity in living human eyes // Investigative Ophthalmology & Visual Science. - 2005. - Vol. 46, no. 2. - P. 409-414.
- Reichel E., Miller D., Blanco E., Mastanduno R. The elastic modulus of central and perilimbal bovine cornea // Annals of Ophthalmology. - 1989. - Vol. 21. - P. 205-208.
- Ridley F. The intraocular pressure and drainage of the aqueous humour // British Journal of Experimental Pathology. - 1930. - Vol. 11, no. 4. - P. 217-240.
- Shin T.J., Vito R.P., Johnson L.W., McCarey B.E. The distribution of strain in the human cornea // Journal of Biomechanics. - 1997. - Vol. 30, no. 5. - P. 497-503.
- Silver D.M., Geyer O. Pressure-volume relation for the living human eye // Current Eye Research. - 2000. -Vol. 20, no. 2. - P. 115-120.


