Оценка уровней шума, создаваемого фрезами при обработке колёсных пар

Введение. Рабочая поверхность колёсных пар обрабатывается специальной фрезой, установленной на длинной оправке. Фреза рассматривается как система с распределённой массой, что позволяет теоретически рассчитать спектры вибрации и шума. В зависимости от соотношения изгиб-ной жёсткости режущего инструмента и опор, виброакустические характеристики фрезы определяются для условий шарнирного и жёсткого закрепления. В данной работе приведены результаты исследования акустических характеристик режущего инструмента.

Результаты исследований. Расчёт уровней звукового давления фрезы основан на цилиндрической модели источника шума. На основе данных работы [1] (без учёта направленности звукового излучения) получены следующие зависимости.

Для условий шарнирного закрепления:

L = 20lg V k + 20lg k - 20lg r + 25lg d + 150,                          (1)

где V k — скорость колебаний на собственной частоте, м/с; k — коэффициент, определяющий собственную частоту колебаний; r — расстояние от источника до точки измерений, м; d — диаметр фрезы, м.

Для условий жёсткого закрепления:

L = 20lg V k + 20lg(2 k - 1) - 20lg r + 25lg d + 165,                      (2)

где V k — скорость колебаний на собственной частоте, м/с; k — коэффициент, определяющий собственную частоту колебаний; r — расстояние от источника до точки измерений, м; d — диаметр фрезы, м.

Снизить шум, излучаемый фрезой, можно двумя способами: установить акустический экран или увеличить диссипативную функцию, фактически определённую эффективным коэффициентом потерь колебательной энергии. Ниже рассматривается именно такой метод — при этом шум снижается в самом источнике его возникновения.

Работа выполнена в рамках инициативной НИР.

С учётом санитарных норм шума ( L c ) и зависимостей (1) и (2) выразим «требуемое значение» скорости колебаний режущего инструмента.

Для условий шарнирного закрепления:

V *2 = 10 0,05 L - lg гГк1^{1 ,г} 2 - 7,5

.

Для условий жёсткого закрепления:

V * 2 = 10 0,05 L c — lg ^r / ( 2 k - 1 ) d ^1,25 - 8

.

Расчётная схема фрезы приведена на рис. 1. Фреза 1 вставляется в отверстие шпинделя 2 , ориентируется шпонками 3 и затягивается шомполом, а другой конец фрезы имеет цилиндрическую цапку, которая поддерживается съёмной стойкой. Съёмная стойка 4 ориентируется по шпонке и крепится к своему основанию 5 . Аналогично производится установка другой фрезы.

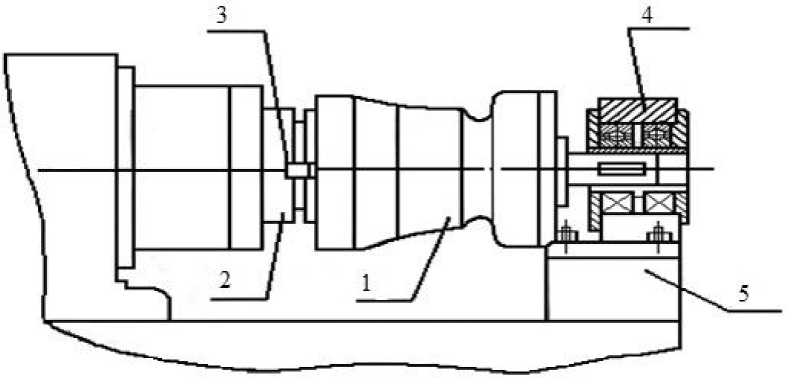
Рис. 1. Установка фрезы на колёсофрезерном станке

При операциях фрезерования сила резания, согласно исследованиям И. Г. Жаркова и нормативам режимов резания, определяется по формулам [1, 2]:

P yz = P yz-' cosn nz " t - ( q - 1 ) г = P yz 'cos H - ( q - 1 ) 7] -               (5)

10 -Ct^xS y * Bⁿ * • z*

P =---p---z--K„, Н zz            dq* nW *             мр- - где t — глубина резания, мм; Sz — подача на зуб фрезы, мм/зуб; B — ширина фрезерования, мм; z* — число зубьев фрезы; d — диаметр фрезы, мм; w — частота вращения фрезы, мин-1; Ср, Кмр, х*, У *, n*, q*, W — коэффициенты, зависящие от обрабатываемого материала фрезы, геометрических параметров режущих пластиков и типа фрез (выбираются по соответствующим таблицам) [2]; q — номер зуба фрезы.

Метод расчёта виброскоростей основан на представлении фрезы как системы с распределёнными параметрами, на которую действуют силовые возмущения от каждого зуба. В этом случае уравнения поперечных колебаний в направлении осей ОZ и ОY фрезы как шарнирно-опёртой системы имеют вид:

д ² У    2d⁴ у 2Py "Г . nkl . nkl,          . п kl_z, )      Г. . ,, ,    ^2n 1 . nkx

—V+а2—r— =—L_у sin—1- + sin—2 + _ + sin —z- • cos 0,1 nz t - (q -1)— • sin---, (7) д t2     дх4 m 0 £11     l l              l J [           (     ) Z ] l d2 z

—7 + a

э d4 z 2Pz       . nkl.     . nkl . nkl, i2—T =---> sin—2 + sin—2 + _ + sin —z*

d x⁴   m R = 1 (     l        l             l

• cos ^0,1 nz-t - ( q - 1 ) z * • sin k , (8)

π kx

l

где Pz , y = P_yz • cos

n n .   / и \ 2п n             * i к 2п

—t - q - 1)— = p • cos toz • t - q - 1)—

30     ⁽      ) z ^{yz               (}      ) z

EY

, a ² = —; q — номер зуба; l i — m ₀

координаты расположения зуба, м; E — модуль упругости, Па; J — момент инерции, м⁴; m 0 — распределённая масса, кг/м ( m 0 = pF , p — плотность материала, кг/м³); F — площадь поперечного сечения, м²; l — длина фрезы, м; n — частота вращения фрезы, об/мин.

Для стали, соответственно, получим:

EJ = 1,7 • 10 6 d 2 ; m_a = 6 • 10 3 d ².

m ₀                 ⁰

Используя метод разделения переменных, систему дифференциальных уравнений приведём к виду:

p y

3 • 10 ³ d ² 1

pz

3 • 10 3 d ² 1

dy +1,7 • 108 d2 dt2

” ( ._n kl.      ._n kl,

> sin—² + sin— ² + _ + sin

^     //

R=1V        'l dz +1,7 • 10‘d 2

^( _n kl ._n kl

У sin—² + sin— ² + _ + sin

^     //

R =1V       ll

। k 1

< l )

π kl £

l

I У =

z *

• cos 0,1 zz*t ^- ( q ^- 1 ) z ⁿ

.

I k 1 1,

π kl l

I z =

z *

• cos 0,1 nzt ^{- (} q ^- 1 ) I ?

.

Решение уравнений относительно скорости колебаний получены в следующем виде:

। ,     p nz*         . п/     . n kl₂          . nkl I

Vkv = ^y л з У sin--- ^L + sin--- ² + ••• + sin z * x

^{1 ky|} 3 • 10 ⁴ d ² l h ( l l                  l J

=X

x sin 0,1 nzt - ( q - 1 ) z ? - 1,7-10 8 d

2 ( - Y

- -1

,

। pnz* ” ( . n kl,      . n kl          . n kl , I

V = ^rz    V sin— 1- + sin— 2 + _ + sin — z * x

^{1 kz|} 3 • 10 ⁴ d ² 1 ^ [ l l                  l I

=X \                                                      /

. 7n _    .

x sin 0,1 nz't - ( q - 1 ) z * - 1,7-10 ⁸ d

,2( k 1 4

- -1

.

Данные выражения не учитывают коэффициента потерь колебательной энергии. Воспользуемся приёмом представления модуля упругости в комплексной форме:

E = Ё ( 1 + jn ) x , где η — эффективный коэффициент потерь колебательной энергии.

Кроме этого следует учесть, что в рамках данной работы ставится задача определения максимального значения уровня звукового давления, возникающего за время фрезерования колёс. Поэтому следует определить максимальное значение скорости колебаний. Тогда выражения (12) и (13) примут вид:

I., I p^nz хД Г . nkl . nkl . nkl_z, I

V  = —У> sin—^L + sin— ² + ^ + sin — z * x

I ky ^ax 3 • 104 d2 lR=1 (      l           l                l J x s

1,7 • 10 8 d ^{2 (} k J'

* ) ² + 3 • 10 ¹⁶ n ² d'

4 I - I

I l J

- 0,5

.

... । pzz ” f . nkl . nkL . nk1 I

V = ^rz —— у sin — ¹ + sin — ² + . + sin — ^z— x

^{1 kz lmax}   3 • 10 ⁴ d ² / £ V     11           1 J

X S

1,7 • 10 8 d ² 1 k )

* ) ² + 3 • 10 ¹⁶ n ² d

⁴ 1 k I

1 1 ^J

- 0,5

>

.

Для расчёта звукового давления определяется среднеквадратичное значение скорости колебаний:

V =

2. max

Фрезы, у которых опоры имеют высокие значения жёсткости, предоставим как жёстко-защемлённые. Тогда дифференциальные уравнения поперечных колебаний (в соответствии с краевыми условиями жёсткого защемления) примут вид:

d ² y ₂ d ⁴ y P Л f . з nk1 . з n k1₂ . з nk1_z, —У + a —у = —У I sin ³—² + sin ³—² +.+ sin ³ — ^z * d t ² d x ⁴ m 0 ^£ V 1 1 1

• gin ³ h- cos ^0,1 nz4 ^- ( q ^- 1 ) Z ^ .(17)

2π

z

d ² z

—- + a d tt

Производя нений:

d ⁴ z dx⁴

от

π kl

= — УI sin ³ ^1 + sin m o k = i I       1

πkl           πkl i3 —p + ...+ sin3 -jz*-

• sin ³ h. cos 0,1 nrt - ( q - 1 ) | Q . (18)

2π

z

аналогичные преобразования, получим следующую систему дифференциальных урав-

dy + 1,7 • 10 8 dd dt ^{2     ,}

^2,5 Py У f ■ 3 nkL    . 3 n k1₂

—-—У У sin³ —² + sin³ —² + . + sin

10 ⁴ d ² 1 £ 1 V       1           1

- f k I 1 1 ^J

π kl ³

l

I y =

Z *

2n

• cos 0,1 n^{zt -(} q - 1 ) z .

dy + 1,4 • 10 ¹⁰ d ² f k J y =

p y

3 • 10 ³ d ² 1

" f . 3 n kJ

У sin ³—1- + sin

^     /

R =1 V          l

π kl           π kl

1 ³ —p + .+ sin ³ 1'"

2n

• cos 0,1 mt ^- ( q ^- 1 ) z

.

2,5 p " f . з n k1 —У-У У sin ³ —² +

10 ⁴ d ² 1 ^£ V      1

d F ⁺ 1,710 " ^{d 2} ( 1 )

π kl             π kl

Sin ³ —z + _ + Sin³ — J

I Z =

Z *

2П

• ^cos 0,1 n^{zt -(} q - 1 ) z -

dd + 1,4 • 10 ¹⁰ d ² 1

dt ²                 V

" f . 3 nk1     . з n k1₂           . 3 nk1 _z.

= y sin ³ —² + sin ³ —² + . + sin ³ — ^z-*

R =1 V

k Y l J z =

2n

• cos 0,1 n^{zt -(} q ^- 1 ) z .

Решение полученной системы уравнений относительно скорости колебаний определяется следу-

ющими выражениями:

।    ।      ^2,5 pn^z "f .   n k1_T     . з n k1₂          . з n k1 _z У

V = — — У sin ³ —² + sin ³ —² + . + sin ³ — ^z * x

I ky dmax      10 4 d ² 1 £ |        1            1                  1 J

R =1 x                                                           ✓

X S

1,7 • 10 8 d ²

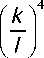
- ( 0,1 zz * ) ²

+ 3 • 10 ¹⁶ n ² d ⁴

k

/

- 0,5

V I = p y nz

I ^{ky 2} I max     3 ■ 10 3 d ² 1

" Г . з n kl     . з n kl

У Sin ³ —1- + Sin ³ —2 +.

R = 1 V          l                 l

XS

1,4 ■ 10 ¹⁰ d ² Г k У

■ 3 n k_z, 1

..+ Sin3 —p Ix л —0,5

+ 2 ■ 10 ²⁰ n ² d ⁴ I kk i

I 2,5 pnz " Г . 3 n kj   .3 n kj

V =--Z z 3— У Sin ³ —Л + Sin ³ —У + — + Sin

I kz ¹'max      10 4 d ² 1 £ 1 (        l             l

х s

1,7 ■ 10 8 d ² Г k ¹

* ) ² + 3 ■ 10 ¹⁶ n ² d

⁴ 1 k I

1 l )

;

3 nkl_z, 1

¹³ — I z I х

3 —0,5

;

I.. I        p_znz    " Г . ₃ п —    ,₃ n kj

V =--- z , , У Sin ³— + Sin³-;-²- + —+ Sin

I kz ² ।max     3 ■ 10 ³ d ² / £ 1 l             l

X s

1,4 ■ 10 ¹⁰ d ² 1 k 1

* ) ² + 2 ■ 10 ²⁰ n ² d

⁴ 1 ^k I

1 l )

3 nkl „ I

— 0,5

.

Скорость колебаний источника в э том случае определяется как

V = V »1L⁺ V y L⁺ V X⁺ V ■[

max .

Соответственно, «требуемые значения» эффективных коэффициентов потерь колебательных энергий получены из выражений максимальных значений скоростей колебаний.

Для условий шарнирного закрепления

₂     k ₁ k ₂

П — ,

-v- k

, Г nz*     1 2

где ^k i "I 3:10 4 5 2 1 J

■ ( P y + P z ) , ^k 2 = ^1,7 • ¹⁰8 d ²

k ₃ k ₅η⁴

—

, ^k3 = ^{340 16 d} 4 1 l

.

Г k k         V k

-— k +   k — kk — kk n ² — к k

1/*2 5    i/*2 3      3 4      2 5 I ।     i/*2 4

V V k         V k                     J V k

— k r k = 0, Vk*²

где k ₆ — 7,5 k 1 , k ₇ — 10 k 1 .

Заключение. Диссипативную функцию узла режущего инструмента можно увеличить, установив оправку с элементами вибродемпфирования и модернизировав правую опору на подшипниках качения. Следует отметить, что увеличения диссипативной функции может оказаться недостаточно для снижения уровней звукового давления режущего инструмента до предельно допустимых значений. В этом случае целесообразно установить акустический экран — упрощённой конструкции, с уменьшенными габаритами.