Оценка устойчивости цифровой системы регулирования многосвязного объекта

Свиридов Д.А., 2012

для многосвязных объектов является достаточно сложной и не вполне решённой задачей на сегодняшний день.

В связи с этим наиболее эффективным подходом для управления такими объектами является робастное управление, которое предусматривает устойчивую работу системы в широком диапазоне и обеспечивает достаточное качество ведения процесса [1].

Для класса технологических объ ектов, характеризующихся многосвязанностью и нестационарным поведением необходимо выбрать критерий, учитывающий качество регулирования и запас устойчивости системы, который в дискретной форме можно представить:

nm

I = Е р j I Е e ji + %м min, (1) j=i V i=i /^р j )

где e - ошибка управления; а - весовой коэффициент, учитывающий соотношение между интегральной квадратичной оценкой и запасом робастной устойчивости; р - весовой коэффициент, учитывающий значимость критерия по каждому выходу системы; р - запас '^^йттттво-сти; n - число выходов системы; m - 35 тво точек переходного процесса.

Примером многосвязного нестационарного объекта управления является процесс получения аммиака [2]. Экзотермический синтез аммиака протекает в 4-полочном реакторе в присутствии катализатора с промежуточным охлаждени ем между слоями. Задачей управления процессом является поддержание температуры в каждом слое катализатора в условиях изменения активности катализатора и теплофизических свойств реактора (рис. 1).

y4

_____________ W o ^,4( z )W p1 ( z ) _____________ + _v ( 1 + W o ^-1 ( z ) W P ( z ) )( 1 + W o ^4,4 ( z ) W p ⁴ ( z ) ) ⁺

w 'ciw (^Wp^W p , ;, 121 ( 1 + w o ^-1 W p )( 1 + W o ^4,4( Z )W p ⁴( Z ) ) 1=1

+

+

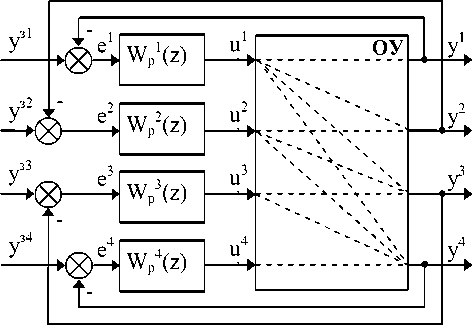
Рис. 1. Схема системы регулирования процесса синтеза аммиака: ОУ – объект управления; y1÷y4 – измеряемые выходы системы (температура в слоях катализатора); yз1÷yз4 – задающие воздействия; е1÷е4 – ошибки регулирования; u1÷u4 – управляющие воздействия (степени открытия заслонок на байпасных потоках); Wр1(z) ÷Wр4(z) – дискретные передаточные функции цифровых регуляторов

W o ^3,4 ( z )W p ³ ( z )W p1 ( z ) ( W o ^1,2 ( z ) W o ^2,3 ( z )W p ² ( z ) ) +

( 1 + W o,' ( , )W p_M )I1 ( 1 + W W )

1=3

)

W o ^3,4( Z )W p ³( Z )W p ( Z ) I W I Z ) )

( 1 + W o¹^ Z )W p1 ( Z ) ) П ( 1 + W o, ¹ W p )

1=3                      7

y³¹ +

_____________ W o ^2,4( Z )W p ²( Z ) _____________ ( 1 + W o ^2,2 ( Z ) W p ² ( Z ) )( 1 + W o ^4,4 ( Z ) W p ⁴ ( Z ) )

-W3,4( z )W2,3( z )W3( z )W2( z )

+--------4-----------p------p

П ( 1 + ^W)

1=2

W^3,4 ( z )W³( z )           W^4,4 W⁴

+ о У / p У z y'3 +__о py'4

™u™\    1 + W^4,4( z )W⁴( z )^y

П ( 1 + W, ;, ¹ Wp )             o ( ) p ⁽)

= W_c^1,4( z )y '1 + W_c^2,4( z )y ' ² + W_c^3,4( z )y ' ³ + W_c^4,4( z )y ' ⁴, (5)

где

Взаимосвязь входов и выходов системы

описывается уравнениями [3]:

W o ^k,j(z) =

B^k,j( Z " 1 )    -j

_Ak,j_{( z}- 1₎ ^z

2 bk,j h=1

• z

-h

y¹ =

W o ^1,1( z )W p ¹( z ) 1 + w o,1 ( z )w p ( z )

/1 = W c1,1 ( z ) y ' ¹,

k,j no

1 - 2 a k, ^j

h=1

• z

-

y

W o ^1,2( z )W p ¹( z )( z ) _ç1    W o ^2,2( z )W p ²( z )   _ç2

—о------------- У +--~-----о--- У

П ( 1 + w o,i w p )       ^{1 +} W o ^{2,2( Z )W} p ^{2( Z} )

1=1

дискретная передаточная функция по основному (k=j) или перекрестному (k≠j) каналу ОУ, k = 1,4, j = k ,4 ; a^k,J , b^k,J , d k ^,J - параметры и

= W_c^1,2( z )y '1 + W_c^2,2( z )y ' ²,                            (3)

число тактов запаздывания передаточной функции основного или перекрестного канала;

z - оператор временного сдвига;

y ³

w (ч\\_Лч_{+ v}( 1 + W_o^u( Z ) W p ( Z ) )( 1 + W^{3 ,3} ( Z ) W_p ³ ( Z ) ) ⁺

W=(z) = Q ^{( Z}) ^p         Pⁱ( z^{- 1})

k р

2 qh h=0

• z

-h

n р

передаточная

-W_o ^1,2 ( z )W o^2,3 ( z )W p² ( z )W p ( z )

+-----------3--------------£

П ( 1+ ^W)

1=1                                   7

^{1 -}2 p h • ^z

h=1

, -h

ç1 y

W o^2,3 ( z )W p² ( z )  _ç2    W o^3,3 ( z )W p³ ( z )   _ç3

3          y 3,33 y

П ( 1 + W o-¹ W p )      ^{1 + W}o ^{( Z} ) ^WP^{( Z} )

1=2

= W_c ^1,3 ( z ) y '¹ + W_c ^2,3 ( z )y '² + W_c ^3,3 ( z ) y '³ ;            (4)

функция цифрового регулятора; qⁱ , pⁱ , – параметры передаточной функции регулятора ; k_р , n_р – порядки числителя и знаменателя передаточной функции регулятора;

W c ^k,j( z ) =

B ck ^,j( * 1 )  z -d^

A k ( z 1 )

k,j

С с + 1 l e k ■ z ^-n n=1

k,j nс

1 -M

В качестве дискретных моделей регуляторов и каналов объекта выбраны следующи е передаточные функции:

n=1

■ z

W р ⁱ(z) =

q °i ^{z - 1 I} q 1i ^{z - 1}

W о ⁱ • ^J(z) =

дискретная передаточная функция замкнутой системы; a ^ck,J , p ^ck,J , d^ck,J - параметры и число тактов запаздывания передаточной функции замкнутой системы, k, J = 1,4 .

b j ^{- 1 - d} '^J

1 + a j- ¹ ’

где i, J = 1,2 .

Численные значения параметров дискретных моделей каналов объекта и цифровых регуляторов приведены в табл. 1 [3].

Исходя из выбранного критерия (1), одной из первых задач, возникающих при синтезе и моделировании робастной системы, является

оценка запаса устойчивости.

Учитывая дискретную форму математического описания системы, для оц енки устойчивости целесообразно применить дискретный корневой критерий, который заключается в оценке положения корней характеристического многочлена системы (2)-(5), записанной в пространстве состояний:

x (k + 1) = A ■ x(k) + b ■ u(k), y(k) = c ^T ■ x (k),

где x – вектор переменных состояния;A – матрица системы; b – вектор передачи управления; c – вектор наблюдения.

Для устойчивости системы регулирования необходимо, чтобы корни характеристического многочлена передаточной функции находились внутри единичного круга [4]:

|«J <  1, i = 1,2...,m, (7) где a i - собственные значения матрицы A .

Оценка устойчивости по первому выходу системы y¹ определяется по передаточной функции системы (2). Для второго и последующих выходов ( y² , y³ , y⁴ ) необходимо учиты-

вать наличие перекрёстных каналов связи.

Для второго выхода системы с учётом перекрёстной связи достаточно рассмотреть корни характеристического многочлена первого слагаемого уравнения связи (3), так как знаменатель второго слагаемого входит в состав первого.

Найдём корни характеристического многочлена передаточной функции:

W_e 1' ²(z) =

W î^1,2 (z)W ð¹ (z)

(1 + W^zW^a + W 1/1W i/n

Таблица 1

Параметры передаточной функции

Канал объекта	Параметры моделей ОУ			Ре-гуля-тор	Параметры регуляторов
	a 1	b, % / ºС	d,такт		q 0	q 1
Wо 1,1	0,901	-0,333	10	W р 1	-0,51	0,49
Wо 2,2	0,916	-0,133	16	W р 2	-0,51	0,49
Wо 1,2	0,927	0,043	18	–	–	–

Отсюда получим

W_e 1’2 (z) =

b₁ 1,2 z

1 + a

(1 +

.-J

- 1-d¹ ’ ²

q₀ 1 z

-J

+ 0 1* 2

-J

1,2

z

-

1 - z

-

b₁ 1,1 z

-

- 1-d¹ ’ ¹

q₀ 1 z

-

+ 0 1* 2

-

X

1 + a

(1 +

b

1,1

z

-

2,2

1 . я 2,2 7-1

1 + a 1 z

1 - z

-

В начале цикла работы катализатора в процессе синтеза аммиака время транспортного запаздывания по каналам не превышает 180 с, что при длительности такта квантования дискретной системы Т 0 =10 с соответствует числам тактов запаздывания d, приведенным в табл. 1. Отсюда передаточная функция (8) примет вид

W^z) =

_{B с} 1,2 _(z)

A с ^1,2(z)^,

где B₆^1l2(z) = b₅z ^{- 23} + b₄z ^{- 22} + b₃z ^{- 21} + b₂z ^{- 20} + b 1 z ^{- 19},

Д         Я  7-31+Я  7-3°+Я  7-29+Я  7-28+ Я  7-21+ х A^   (z)    a19z     I ^*18z      i ^a 17z      I ^*16z      + ^*15z

+ Я 7-2°+Я 7-19+Я  7-18+Я 7-17+Я 7-15+ Я 7-14 4-

I ^114 z      I ^113 z      I ^112 z      I ^111 z      I ^11° z       I ^19 z

-13 .         -12 .         -11 .         -5 .         -4 .

I a 8 z    I a 7 z    I a 6 z    I a 5 z   I a 4 z   I a 3 z I

I a2z  I a1z— 1.

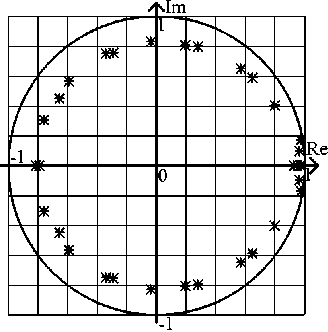
Рис. 2. Расположение корней характеристического многочлена

По условию (7) можно сделать вывод, что система устойчива. Динамические характеристики системы, представленные на рис. 3, подтверждают полученную оценку корневого критерия.

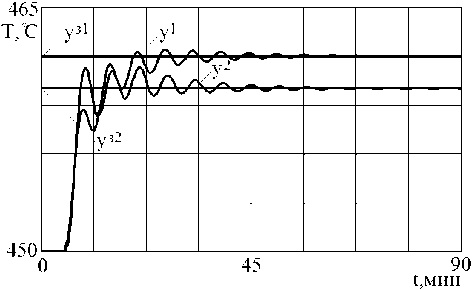
Рис. 3. Динамические характеристики системы в начале цикла работы катализатора

В процессе работы реактора синтеза аммиака повышается инерционность по каналам объекта. В конце эксплуатационного пери ода катализатора величина чистого запаздывания по каналам составляет d^1,1 = 13, d^1,2 = 22, d^2,2 = 20 (табл. 1) . Полиномы передаточной функции (9) примут вид (рис. 2):

B₆^1,2(z) = b 5 z ^{- 28} + b₄z ^{- 27} + b₃z ^{- 26} + b₂z ^{- 25} + b 1 z ^{- 24},

Д 1,2             -38        -37         -36         -35

x A^ (Z) a^z    + d1sZ    + anz    + a^z + a^z

. _    _-24 . _      -23  . _ -22  . _      -21  . _      -18 . _-17 .

+a.14Z + a^z  + a^z  + ^nZ  + OiqZ + a^z

+ a₈z ^{- 16} + a₇z ^{- 15} + a₆z ^{- 14} + a₅z ^{- 5} + a₄z -4 + a₃z ^{- 3} +

+ a 2 z + a 1 z —1.

При этом расположение корней характеристического многочлена показано на рис.4.

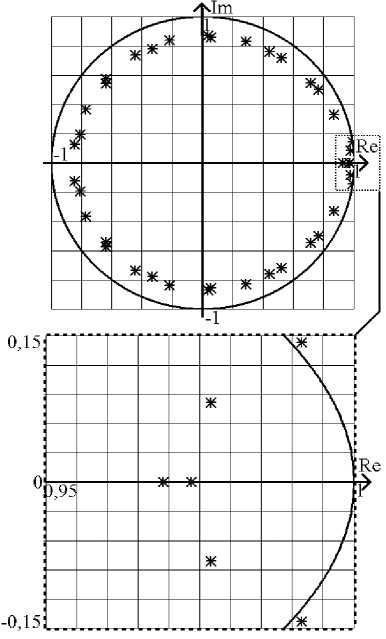
Рис. 4. Расположение корней характеристического многочлена в конце эксплуатационного периода катализатора

Повышение инерционности по каналам объекта приводит к увеличению числа корней характеристического многочлена системы , росту их величин |a _max| = 1,00181 >  1 и, как следствие, к неустойчивой работе системы, что подтверждается динамическими характеристиками на рис. 5.

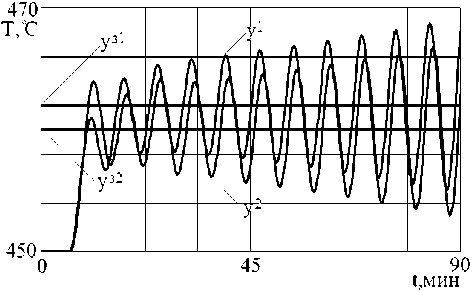
Рис. 5. Динамические характеристики системы в конце цикла работы катализатора

Для оценки устойчивости в течение всего цикла работы катализатора проведено моделирование системы в различных временных интервалах работы реактора (табл. 2).

Таблица 2

Значения максимальных корней в различные периоды работы реактора

№ интервала	Запаздывание по каналам объекта			|α max |
	d 11	d 12	d 22
1	10	18	16	0,98959
2	11	19	17	0,99472
3	12	20	18	0,99869
4	13	22	20	1,00181
5	14	24	22	1,00428

Hа рис. 6. показан характер измен ения максимальных значений корней характеристического полинома.

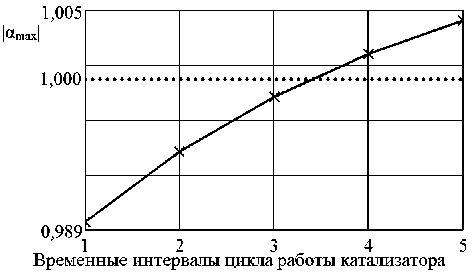
Рис. 6. Зависимость максимальных значений корней в течение всего цикла работы катализатора

Для оценки запаса устойчивости η в критерии робастности (1) целесообразно воспользоваться минимальным отклонением:

η= 1 -α _max ,

Для третьего (4) и четвертого (5) выходов системы оценка устойчивости проведена аналогично.

Рассмотренный подход к оценке устойчивости многосвязной системы регулирования может быть эффективно использован при синтезе робастных систем управления многомерными технологическим объектами.