Оценка устойчивости многосвязной цифровой системы управления процессом экстрактивной ректификации

В результате анализа технологического

Большинство технологических объектов характеризуется нестационарностью динамических характеристик, что с течением времени может привести к снижению качества работы системы управления и потере устойчивости. В настоящее время существует большое число подходов к синтезу систем управления такими объектами, среди которых можно выделить:

─ теорию адаптивных систем;

─ теорию систем с элементами нечёткой логики;

─ теорию нейронных сетей;

─ теорию робастного управления.

Несомненно, каждый из них имеет как достоинства, так и недостатки, однако в ряде случаев использование теории робастного управления позволяет упростить как синтез, так и реализацию системы с обеспечением требуемого качества управления на всём эксплуатационном периоде работы технологического объекта [1]. При этом одной из важнейших задач при аналитическом проектировании робастныхсистем автоматического управления является обеспечение устойчивого состояния и определение запаса устойчивости в рабочем диапазонеизмене-ния технологических параметров объекта. Применение большинства существующих методов оценки устойчивости ориентировано на аналоговые системы, математическим аппаратом которых являются дифференциальные уравнения. Использование этих методов для анализа устойчивости цифровых систем управленияза-труднительно и не всегда корректно, а для многосвязных нестационарных объектов – практически нереализуемо. Отсюда возникает задача разработки алгоритма оценки устойчивости многосвязных цифровых систем управления.

Результаты и обсуждение

В качестве примера рассмотрим двумерный объект – технологический процесс экстрактивной ректификации (ЭР), предназначенный для выделения дивинила-сырца из бути-лен-дивинильной фракции (БДФ) в присутствии диметилформамида, используемого как экстрагент. В процессе ЭР БДФ дивинил является целевым продуктом, качество которого определяется требованиями процесса полимеризации, поэтому основной задачей управления является стабилизация состава дивинила-сырца и уменьшение потерь дивинила с бутиленовой фракцией.

процесса выявлены управляющие и управляемые параметры [2]:

─ управляющие параметры – расход флегмы u ¹ и расход теплоносителя в куб колонны u ² ;

─ управляемые параметры – концентрация бутиленов в дивиниле-сырце y ² и потери дивинила с бутиленовой фракцией y ¹ ;

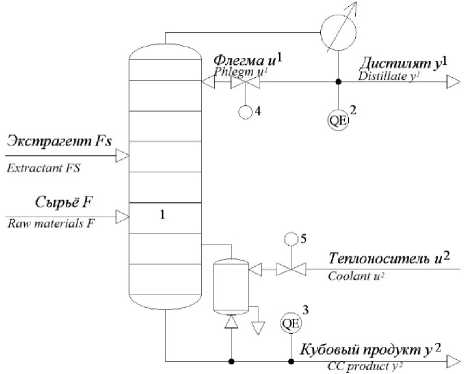
Рисунок 1. Схема процесса экстрактивной ректификации: 1 – колонна; 2, 3 – датчики концентраций дивинила в дистилляте и бутиленов в кубовом продукте; 4, 5 – регулирующие клапаны подачи флегмы на орошение и теплоносителя в куб колонны

• Figure 1.    Scheme of extractive distillation process : 1 – column; 2, 3 – butadiene concentration detectors in the distillate and butenes in a cube product; 4, 5 – regulating filing reflux valves for irrigation and coolant in the cube of the column

Анализ технологического процесса, проведённый на основе исследования статических и динамических режимов работы установки, позволяет сделать вывод, что на показатели качества – концентрацию дивинила в дистилляте y ¹ и концентрацию бутиленов в кубовом продукте y ² – наиболее существенное влияние оказывают расход флегмы u ¹ расход теплоносителя в куб колонны u ² соответственно. Кроме того, существуют внутренние перекрёстные связи между параметрами процесса [2, 3].

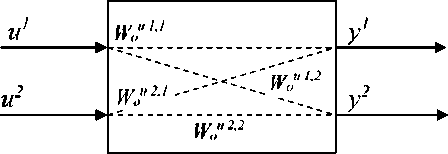
Рисунок 2. Структурная схема взаимосвязей параметров процесса

• Figure 2.    Interconnections block diagram of process parameters

  Основные каналы: W о ^u1,1 – расход флегмы ( u ¹ ) – концентрация дивинила в дистилляте ( y ^u1,1 ); Wоu2 ^,2 – расход пара в куб колонны – концентрация бутиленов в кубовом продукте ( y ^u2,2 ). Перекрёстные каналы: W о ^u1,2 – расход флегмы ( u ¹ ) – концентрация бутиленов в кубовом продукте ( y ^u1,2 ); W о ^u2,1 – расход пара в куб колонны – концентрация дивинила в дистилляте ( y ^u2,1 ).

  Рассмотрим простейший вариант системы – управления, включающий два регулятора обратной связи.

  
  

  i j=1 2 ; a_с ^{i j} , b_с ^{i j} , d_с ^{i j} – то же для передаточных функций системы, k ⁱ , n ⁱ – порядки числи-

  
  

  теля и знаменателя; z – оператор сдвига.

  Дискретная передаточная функция циф-

  
  

  рового регулятора:

  
  

  W p ⁱ (z)=

  
  

  Q ⁱ (z ^-1 ) ₌ u ⁱ (z)

  P ⁱ (z ^-1 )    e ⁱ (z)

  
  

  ⁱ

  ^{k р}          -h-dⁱ

  Z q h^x z р

  h=0

  nⁱ_р

  1 - Z p^z -h

  h=1

  
  
  

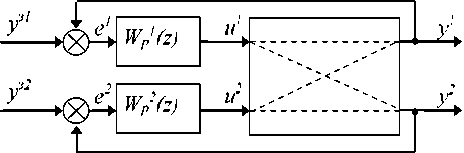
  Рисунок 3. Структурная схема системы управления

  Figure 3. Block diagram of the control system

  
  

  где Q ⁱ (z ^-1 ) , P ⁱ (z ^-1 ) – полиномы числителя

  
  

  и знаменателя, i = 1 2 ; q ⁱ , p ⁱ , d ⁱ _р – настроечные параметры дискретной передаточной функции цифрового регулятора; k ⁱ _р , n ⁱ _р – порядки числителя и знаменателя передаточной функции; u ⁱ (z) – выходы регуляторов.

  Из системы (1), получим уравнения связи

  
  

  Опишем замкнутую систему в матричной форме:

  е = y^з-y,

  u = W р ^u·е,                (1)

  y = W о ·u,

  где e – вектор ошибок управления; y^з – вектор задающих воздействий; y – вектор выходов ОУ; и – вектор управляющих воздействий; W о , W р –

  
  

  по каждому выходу:

  w p (W + П ( w p ) | П ( wy ) - w o • W • ¹ ) y ¹ = —2------=1 ----^^^- y ^{31 +}

  П ( 1 + W O" w p ) - П ( w p ) ( w w- ■ ¹ )        ⁽²⁾

  i=1                         i=1

  
  

  соответственно матрица дискретных переда-

  
  

  W o^{2 , 1} (z)W p¹ (z)

  +₂₂y n ( 1 + W O ' i w p ) - n ( w p )( W o^{1 ,} 2 W 2¹ ) i=1                         i=1

  = W C • 1 (z)y ³¹ +W_c ² • 1 (z)y ³²

  
  

  точных функций объекта по основным и пере-

  
  

  крёстным каналам, 2 х 2 и диагональная матрица цифровых регуляторов, 2 х 2.

  
  

  2                   W o ^{1 , 2} (z)W p ² (z)                  з1

  y=₂₂   y+

  П ( j + W O ' W pi ) - П ( w p )( W 1² W² ; ' )

  
  

  W ^u o

  
  

  _Wu1,1_(z) o

  _Wu1,2_(z) o

  
  

  Wu²’1(z)

  ⁰      , W

  W^u2,2(z)   р

  o _

  
  

  W¹ (z)     0

  ^р

  0    W² (z)

  ^р

  
  
  
  

  Дискретные передаточные функции по каналам объекта ( W о ) и замкнутой системы по каждому выходу ( W с ) имеют следующую структуру:

  
  

  W²_p(z)W²-² + П ( w p ) [ П ( w o • - ■) - w^w o-¹ 1

  ⁺-----2 ---------^ 2=1  y ³²

  П ( 1 + wyw p ) - П ( w p )( w p^ w² ; ¹ )

  i=1                          i=1

  = W’ ;² (z)y ³¹ +W_c ^2,2 (z)y ³²

  
  

  W о,ⁱc^,j (z)=

  
  

  _{B о,c}i j _(z -1 _{) ×z-d iо,,jc}

  _Aо,ci j_(z-1₎

  
  

  k _с i j +1

  i j -h о,ch

  
  

  i j

  n _с

  i j        -h

  о,ch

  
  

  ×z

  
  

  i j о,c

  
  

  ^,

  
  

  где B ^{i j} (z ^-1 ) , A ^{i j} (z ^-1 ) – полиномы числителя о,c               о,c

  
  

  и знаменателя передаточной функции канала объекта или замкнутой системы соответ-

  
  

  ственно, i j=1 2 ; a_о ^{i j} , b_о ^{i j} , d_о ^{i j} – параметры

  
  

  передаточных функций и число тактов запаздывания основных и перекрёстных каналов,

  
  

  Для решения поставленной задачи разработан алгоритм оценки запаса устойчивости многосвязных цифровых систем управления на основе дискретного корневого критерия, включающий следующие основные этапы:

  • 1.    Получение характеристического полинома замкнутой системы по каждому выходу.

  • 2.    Вычисление собственных значений матрицы системы в пространстве состояний с целью определения корней характеристического уравнения и устойчивости системы.

  • 3.    Определение устойчивости и её запаса по величине отклонения модуля максимального корня от границы устойчивости.

  
  

Анализ уравнений связи (2, 3) показывает, что знаменатели передаточных функций замкнутых систем по первому и второму выходам идентичны, следовательно, для получения характеристического полинома системы рассмотрим знаменатель передаточной функции по первому выходу W_c ^{1 , 1} (z) :

w ' (z)w o , + П ( W p ) [ П ( w o" ) - w ^, 2 W 2 ^,1

w c , ' (z) =---2------=-----Ч¹--------------

П ( i+w o , w p ) - n ( w p )( w ■ 2 W 2 ■ ¹ ) i=1                        i=1

Для получения характеристического полинома замкнутой системы в качестве дискретных моделей регуляторов и каналов объекта используем передаточные функции первого порядка:

_i        q ₀ i +q ₁ i z -         _i,j         b ₁ ,j z - -

W р (z)= 1-z_-1   , W о (z)=1+a_1i,jz_-1,

Отсюда, передаточная функция замкнутой системы по первому выходу примет вид:

x

W c^1,1 (z)=

B с ^1,1 (z) _{A с} 1,1 _(z)

q ₀ 1 +q ₁ 1 z -1 b₁ 1,1 z -1-d^1,1 1-z ^-1     1+a₁ ^1,1 z ^-1

_{1 +} b l'^- 'd¹ q ?⁺ q ?^z- Y _{1 +} b?'²^¹ " q Q +q l z ¹ l+a l'V 1-z ^- J|    7+a₁ ²'² z ^-1    1-z ¹

q ₀ 1 +q ₁ 1 z -1 q₀ 2 +q₁ 2 z -1 b₁ 1,2 z -1-d^1,2 b₁ 2,1 z -1-d^2,1

1-z ^-1        1-z ^-1     1+a₁ ^1,2 z ^-1 1+a₁ ^2,1 z ^-1

+

q ? +q ? z ^- q?+q?z ^- Г b?^ ^1-1' '' b^z ¹¹ ”   b₁¹²z ^1-1'¹ b₁ 2 z '

1-z ^-        1-z ¹ I 1+a₁ ¹'¹ z ^-1 1+a ?'² z ^-1   1-u   ² z ^-1 1+a ?'¹ z ^-1

^<Г _{1 +} b ^ z ^1-'¹ q O^^ If _{1 +} b_J^z -^1-2_ q o² +q i^! z ¹ )

|   1+a'' 'z-1    1-z1 J|   1+a?' 2z-1    1-z* J qo'+q''z-' qo2+q?z' b?2z1d1’2 b;L''zJ'1,’1

_v"     1-z ^-'         1-z ^-'     1+a '¹'² z ^-1 1+a ?' ' z ^-1               ,

Параметры моделей системы управления

Таблица 1

Options of control system models

Table 1

Канал объекта	Длительность такта квантования Т 0 , мин	Параметры моделей ОУ			Регулятор	Параметры регуляторов
		a 1	b i , %/ºС	d , такт		q 0	q 1
W0 1 1	1,2	0,958	-0,204	18	Wp 1	-0,0896	0,0831
W0 2 2		0,974	-0,293	5	Wp 2	-0,289	0,273
W0 1 2		0,983	0,016	11	–	–	–
W0 2 1		0,982	0,094	40	–	–	–

Номинальное состояние объекта управления с рассчитанными при этом оптимальными настройками цифровых регуляторов характеризуется параметрами, представленными в таблице 1.

Полиномы числителя и знаменателя передаточной функции W_с ^{1 1} (z) будут иметь следующий вид:

B e ¹ ■ ' (z) = b 57 z⁵ + b 56 z⁵ + b 55 z⁵ + b 54 z 5 + + b J^ z ⁵³ + b 29Z ²⁹ + b 2 ₈z ²⁸ + b 27Z ²⁷ + b 26 z²⁶ + + b 2₅Z ²⁵ + b 2^ z ²⁴ + b 23Z ²³ + b 22 z ²² + b 2'Z 2' + -20          -19

+b ₂₀ z  + b ₁₉z

A_с^{1 , 1}(z) = a ₅₇z^-57 + a ₅₆z^-56 + a ₅₅z^-55 + a ₅₄z^-54 + a ₅₃z^-53 + + a ₂₉z -29 + a ₂₈z -28 + a ₂₇z -27 + a ₂₆z -26 + a ₂₅z -25 + a ₂₄z -24 + -23           -22           -21           -20           -19           -11

+ a ₂₃ z  + a ₂₂ z  + a ₂₁ z  + a ₂₀ z  + a ₁₉ z  + a ₁₁ z +

+ a ₁₀z^-10 + a ₉z^-9 + a ₈z^-8 + a ₇z^-7 + a ₆z^-6 + a ₅z^-5 + a ₄ z^-4 + + a ₃z^-3 + a ₂z^-2 + a ₁z^-1 -1.

Структура коэффициентов характеристического полинома A_с ^{1 , 1} (z) , состоящих из параметров передаточных функций каналов объекта и регуляторов, приведена в таблице 2.

Таблица 2

Составляющие коэффициентов характеристического полинома

The components of the characteristic polynomial coefficients

Table 2

Коэффициент полинома	Многочлены слагаемых полинома
a 1	–(– a 111 a 122 b 12 b 21 q 111 q 122 )
a 2	–( a1 11 b 12 b 21 q1 11 q1 22 + a1 22 b 12 b 21 q1 11 q1 22 – a1 11 a1 22 b 12 b 21 q0 11 q1 22 – a1 11 a1 22 b 12 b 21 q1 11 q0 22 )
a 3	–( a1 11 b 12 b 21 q0 11 q1 22 – b 12 b 21 q1 11 q1 22 – a1 11 b 12 b 21 q1 11 q0 22 + a1 22 b 12 b 21 q0 11 q1 22 + a1 22 b 12 b 21 q1 11 q0 22 – a1 11 a1 22 b 12 b 21 q0 11 q0 22 )
a 4	–( a1 11 b 12 b 21 q0 11 q0 22 – b 12 b 21 q1 11 q0 22 – b 12 b 21 q0 11 q1 22 + a1 22 b 12 b 21 q0 11 q0 22 )
a 5	–(– b 12 b 21 q 011 q 022 )
a 6	–( a 112 a 121 b 11 b 22 q 111 q 122 )
a 7	–( a 112 a 121 b 11 b 22 q 011 q 122 – a 121 b 11 b 22 q 111 q 122 – a 112 b 11 b 22 q 111 q 122 + a 112 a 121 b 11 b 22 q 111 q 022 )
a 8	–( b 11 b 22 q 111 q 122 – a 112 b 11 b 22 q 011 q 122 – a 112 b 11 b 22 q 111 q 022 – a 121 b 11 b 22 q 011 q 122 – a1 21 b 11 b 22 q1 11 q0 22 + a1 12 a1 21 b 11 b 22 q0 11 q0 22 )
a 9	–( b 11 b 22 q 011 q 122 + b 11 b 22 q 111 q 022 – a 112 b 11 b 22 q 011 q 022 – a 121 b 11 b 22 q 011 q 022 )
a 10	–( b 11 b 22 q 011 q 022 )
a 11	–( a 112 a 121 a 122 b 11 q 111 )
a 19	–( a1 12 a1 21 a1 22 b 11 q0 11 – a1 12 a1 22 b 11 q1 11 – a1 21 a1 22 b 11 q1 11 – a1 12 a1 21 b 11 q1 11 – a1 12 a1 21 a1 22 b 11 q1 11 )
a 20	–( a 112 b 11 q 111 + a 121 b 11 q 111 + a 122 b 11 q 111 – a 112 a 121 b 11 q 011 + a 112 a 121 b 11 q 111 – a 112 a 122 b 11 q 011 – a1 21 a1 22 b 11 q0 11 + a1 12 a1 22 b 11 q1 11 + a1 21 a1 22 b 11 q1 11 – a1 12 a1 21 a1 22 b 11 q0 11 )
a 21	–( a 112 b 11 q 011 – b 11 q 111 + a 121 b 11 q 011 – a 112 b 11 q 111 – a 121 b 11 q 111 + a 122 b 11 q 011 – a 122 b 11 q 111 + a 112 a 121 b 11 q 011 + a 112 a 122 b 11 q 011 + a 121 a 122 b 11 q 011 )
a 22	–( b 11 q 111 – b 11 q 011 – a 112 b 11 q 011 – a 121 b 11 q 011 – a 122 b 11 q 011 )
a 23	–( b 11 q 011 )
a 24	–( a 111 a 112 a 121 b 22 q 122 )
a 25	–( a1 11 a1 12 a1 21 b 22 q0 22 – a1 11 a1 21 b 22 q1 22 – a1 12 a1 21 b 22 q1 22 – a1 11 a1 12 b 22 q1 22 – a1 11 a1 12 a1 21 b 22 q1 22 )
a 26	–( a 111 b 22 q 122 + a 112 b 22 q 122 + a 121 b 22 q 122 – a 111 a 112 b 22 q 022 – a 111 a 121 b 22 q 022 + a 111 a 112 b 22 q 122 + a 111 a 121 b 22 q 122 – a 112 a 121 b 22 q 022 + a 112 a 121 b 22 q 122 – a1 11 a1 12 a1 21 b 22 q0 22 )
a 27	–( a 111 b 22 q 022 – b 22 q 122 – a 111 b 22 q 122 + a 112 b 22 q 022 + a 121 b 22 q 022 – a 112 b 22 q 122 – a1 21 b 22 q1 22 + a1 11 a1 12 b 22 q0 22 + a1 11 a1 21 b 22 q0 22 + a1 12 a1 21 b 22 q0 22 )
a 28	–( b 22 q 122 – b 22 q 022 – a 111 b 22 q 022 – a 112 b 22 q 022 – a 121 b 22 q 022 )
a 29	22  22    11   12  21  22 –( b q 0 + a 1 a 1 a 1 a 1 )
a 53	–(– a 111 a 112 a 121 – a 111 a 112 a 122 – a 111 a 121 a 122 – a 112 a 121 a 122 –2 a 111 a 112 a 121 a 122 )
a 54	–( a1 11 a1 12 + a1 11 a1 21 + a1 11 a1 22 + a1 12 a1 21 + a1 12 a1 22 + a1 21 a1 22 +2 a1 11 a1 12 a1 21 + 2 a1 11 a1 12 a1 22 + 2 a 111 a 121 a 122 + 2 a 112 a 121 a 122 + a 111 a 112 a 121 a 122 )
a 55	–( a 111 – a 112 – a 121 – a 122 –2 a 111 a 112 –2 a 111 a 121 –2 a 111 a 122 –2 a 112 a 121 –2 a 112 a 122 –2 a 121 a 122– 11   12  21    11   12  22    11  21  22    12  21  22 a 1 a 1 a 1 – a 1 a 1 a 1 – a 1 a 1 a 1 – a 1 a 1 a 1 )
a 56	–(2 a 111 + 2 a 112 + 2 a 121 + 2 a 122 + a 111 a 112 + a 111 a 121 + a 111 a 122 + a 112 a 121 + a 112 a 122 + a 121 a 122 +1)
a 57	–(– a 111 – a 112 – a 121 – a 122 –2)

Представим знаменатель (4) в виде матрицы коэффициентов в переменных состояния:

	" 0	... о	о •■•	0	0	... о	о"
	0	... о	о •■•	0	0	... о	о
	0	... о	о •■•	0	0	... о	о
	0	...     1	о •■•	0	0	... о	о
A =	0	...    о . •      :	1 .	0	0	... о .   :	о
	0	... о	о •■•	0	0	... о	о
	0	. о	о •■•	0	0	..    1	о
	0	. • о	о .	0	0	.. о	1
	_ a57	. a53	о .	0	a11	. а2	а1.

Анализ структуры коэффициентов полинома знаменателя передаточной функции (таблица 2) и матрицы коэффициентов в переменных состояния позволяет сделать следующие выводы:

─ численные значения коэффициентов характеристического полинома А с ^{1 ,} 1 (z) определяются значениями параметров моделей всех каналов и регуляторов;

─ при неизменных порядках моделей каналов, регуляторов и значениях транспортного запаздывания структура коэффициентов полинома и размерность матрицы в переменных состояния сохраняются, при этом собственные значения матрицы будут изменяться в условиях нестационарности;

─ значительное влияние на структуру коэффициентов полинома оказывает изменение структуры моделей каналов и регуляторов, а также величины транспортного запаздывания по любому каналу объекта.

─ Таким образом, в соответствии с предложенным алгоритмом для оценки устойчивости системы необходимо:

─ вычислить коэффициенты характеристического полинома на основе численных значений параметров дискретных моделей каналов объекта и настроек цифровых регуляторов (таблица 1).

─ определить собственные значения матрицы коэффициентов в пространстве состояния, которые являются корнями характеристического уравнения замкнутой системы.

Определив корни характеристического уравнения, покажем характер их расположения на комплексной плоскости:

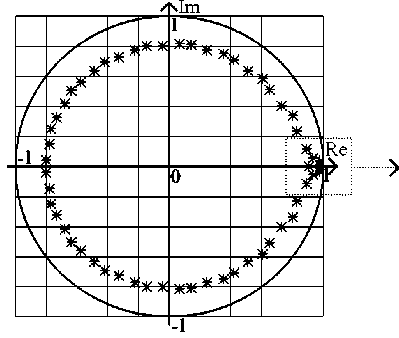
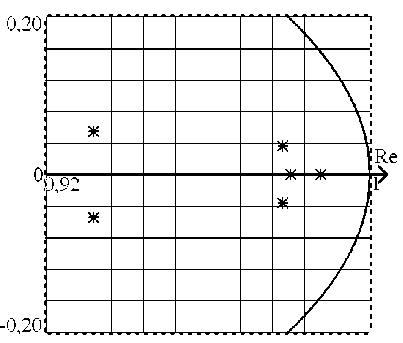
Рисунок 4. Расположение корней характеристического уравнения

Figure 4. Characteristic equation roots location

Анализ численных значений корней и характер их расположения на комплексной плоскости, позволяют сделать вывод, о том, что система устойчива. Для подтверждения полученных результатов проведено моделирование работы замкнутой системы. Динамические характеристики подтверждают полученную оценку корневого критерия.

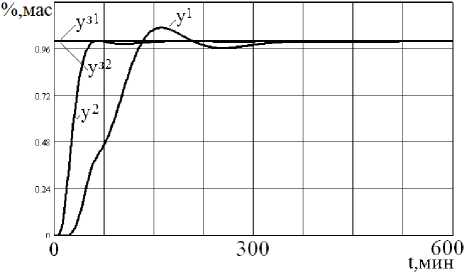
Рисунок 5. Динамические характеристики системы в приращениях при номинальном состоянии объекта

Figure 5. The dynamic characteristics of the system in increments at the object nominal state

Как указывалось выше с течением времени, возможно, изменение как параметров моделей каналов, так и транспортного запаздывания. Однако изменение транспортного запаздывания по любому из четырёх каналов объекта приводит к изменению структуры коэффициентов характеристического полинома и к изменению размерности матрицы в пространстве состояния.

Для доказательства работоспособности алгоритма рассмотрим случай увеличения транспортного запаздывания по всем каналам объекта одновременно. Такая ситуация может быть обусловлена образованием полимера и ухудшением теплообмена в кипятильниках, конденсаторах, забивкой микропримесями и полимером клапанов тарелок колонны и другими причинами [2, 3], что неизбежно приводит к увеличению транспортных запаздываний (таблица 1) по каналам объекта ( d ^1,1 = 56, d ^1,2 = 12, d ^2,1 = 41, d ^2,2 = 6 ). В этом случае полиномы примут вид:

B* , 1 (z) = b 66 z ⁶ + b 65 z ⁶ + b 64 z ⁶ + b 63 z ⁶ + + b 62Z⁶⁶ + b ₆^ ⁶ + b -2 z ⁶⁰ + b 63 z ^-5 + b ^ + + b ₃₀z ^-57 + b ₂₉z ^-56 + b ₂₈z ^-55 + b ₂₇z ^-54 + b ₂₆z ^-53 , 1 , 1                -66           -65           -64           -63

A C ^(z) = a 66 z ⁺ a 65 ^{z +} a 64 ^{z +} a 63 ^{z +}

+a,,z-"+ a z 61 + a z 60 + a,0z59 + a,„z58 + 62          61          60          5958

57          56          55          5453

+a, 7z + a, ,z + a, z + a, .z + a, ,z + 57          56          55          5453

+a,, zn + a, z10 + a0 z-9 + a8 z8 + a7 z- + a,, z-6 + 11           10           9          8          76

+ a ₅z ^-5 + a ₄z ^-4 + a ₃z ^-3 + a ₂z ^-2 + a ₁z ^-1 -1.

Изменение числа коэффициентов, повлечёт изменение как их структуры, так и размерности матрицы А . Вычисляя собственные значения, покажем корни на комплексной плоскости:

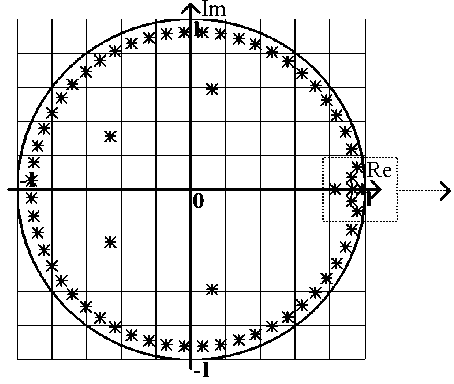
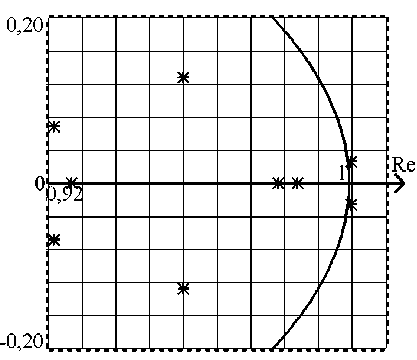
Рисунок 6. Расположение корней характеристического уравнения

• Figure 6.    Characteristic equation roots location

  Увеличение инерционности по каналам объекта приводит к увеличению числа корней характеристического многочлена системы, росту их величин | 2 _max | = 1,00093 >  1 и, как следствие, к неустойчивой работе системы, это подтверждается динамическими характеристиками, полученными при моделировании.

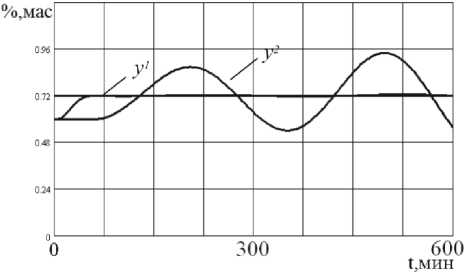
Рисунок 7. Динамические характеристики системы при увеличении транспортного запаздывания

• Figure 7.    The dynamic characteristics of the system in increments within increasing transport lag

Для оценки запаса устойчивости цифровой многосвязной системы в работе предложено использовать минимальное отклонение от границы устойчивости:

П = * — V ^L mxx\ , где η – запас устойчивости.

Заключение

Рассмотренный подход к оценке устойчивости многосвязной системы регулирования может быть эффективно использован в автоматизированном режиме при синтезе робастных систем управления многомерными технологическими объектами.