Оценка VaR портфелей с применением методов понижения размерности PCA и RPCA

Каждой компании и каждому банку необходимы методы измерения и контроля своих финансовых рисков для различных будущих сценариев, чтобы поддерживать целевой рейтинг. Поэтому задача оценки финансового риска является одной из важнейших в финансовой математике. Формально, если X — случайная величина, описывающая прибыль компании, то по ней нужно определить возможные убытки на определенном временном интервале. Функции, оценивающие значение риска на основе X, называются мерами риска.

Наиболее распространенной на практике одномерной мерой риска является VaR (Value at Risk). Простыми словами, VaR уровня а показывает, что убытки компании будут превышать значение VaR_a с вероятностью не более а.

Если в портфеле инвестора или компании есть только один актив, то оценка параметров одномерного распределения и вычисление VaR являются стандартной задачей [1]. Однако, если портфель состоит из большого количества активов, которые сильно коррелируют, задача становится намного сложнее, так как необходимо оценивать совместное d-мерное распределение активов, где d — количество различных активов в портфеле. Данная проблема с использованием корреляционного подхода описывается, например, в работах [2-4]. В условиях эпохи больших данных и доступности новых источников информации (например, социальных сетей, ESG-факторов, новостных потоков) объем данных, используемых для управления рисками, значительно вырос [3]. Это делает классические методы, такие как прямое использование ковариационной матрицы или простые факторные модели, неэффективными из-за вычислительных ограничений и риска переобучения.

Один из распространенных методов оценки VaR и поиска оптимального портфеля — метод Монте-Карло (см. [5,6]). Метод Монте-Карло предполагает многократную генерацию различных портфелей и вычисление их параметров, что становится вычислительно крайне сложным, а также требует предположений о совместном d-мерном распределении цен активов.

Более того, важно отдельно отметить, что при решении задачи оптимизации портфеля критически важно не просто уметь оценивать риск для конкретного портфеля, но и иметь многомерную модель, из которой можно быстро получить оценку риска для любого набора весов. В противном случае для каждого нового варианта распределения весов (каждого нового портфеля) пришлось бы заново обучать модель, что крайне неэффективно с точки зрения вычислительных затрат. Таким образом, наличие универсальной многомерной модели, позволяющей производить оценку VaR без переобучения при смене весов, существенно упрощает и ускоряет решение задачи оптимизации крупного портфеля. Так как решение многомерной задачи оптимизации при высоких размерностях напрямую вычислительно крайне затруднительно, зачастую для решения этой проблемы предлагается использовать методы понижения размерности, в частности Principal Component Analysis (далее — РСА), введенный в работе [7]. Применение метода РСА к оценке финансовых рисков описано в многочисленных работах, см., например, [8-11].

В работе [12] авторы с применением РСА выделили некоррелированные компоненты, которые являются линейными комбинациями исходных активов и объясняют достаточную долю дисперсии портфеля, а затем, основываясь на них, упростили построение границы эффективных портфелей в задаче Марковитца, введенной в работе [13]. На основе полученного подхода в работе [14] авторы применили метод выделения главных компонент для определения диверсифицированности портфеля. В [15,16] данный подход обобщен так, что максимально диверсифицированные портфели должны включать в себя активы в практически одинаковых долях, минимизируя при этом дисперсию доходности портфеля.

В данной работе также рассматривается альтернативный подход к понижению размерности портфеля, основанный на Probabilistic PC А (далее — РРСА), введенный в работе [18]. В отличие от РСА данный метод предполагает вероятностную модель данных и оптимизирует не долю объясненной дисперсии, а функцию правдоподобия. Таким образом, за счет вероятностной модели и отдельной оценки шума с помощью РРСА можно лучше оценить VaR, чем используя РСА (данный подход хорошо работает для приближения совместного распределения коррелированных данных (см. [19], [20])). Однако алгоритм редко применяется для финансовых данных (см. [21]), что делает актуальным его исследование в применении к задаче оценки финансового риска.

Таким образом, новизна данного исследования заключается в следующем:

• •    использование РРСА для оценки VaR₅% и сравнение результатов с классическим подходом на основе РСА (5 % — стандартное значение, принятое в индустрии);

• •    подбор оптимального размера окна для оценки VaR^% вместо использования случайного размера окна или найденного только из экономических соображений;

• •    проведение полномасштабного бэктестинга на длительном временном промежутке (более 15 лет) и широком наборе портфелей, отражающих разнообразные варианты поведения.

Актуальность работы обусловлена потребностью в более точных и гибких методах оценки риска в условиях постоянно растущей размерности портфелей и усложняющихся корреляционных структур. Применение РРСА совместно с оптимизацией временного окна обеспечивает статистически более обоснованную и практически применимую оценку VaR.

• •    слабо диверсифицированные: 200 случайных портфелей, в которых 1-5 ведущих акций сосредоточивают 90 % весов;

• •    диверсифицированные: 200 случайных портфелей, в которых веса случайным образом распределены между всеми акциями.

2.    Основные понятия2.1.    Value at Risk 2.2.    PCA (метод главных компонент)

На основе подходов РСА и РРСА для каждого момента времени получаются оценки VaR^%, после чего их качество проверяется на основе проведения бэктестинга. Полученные результаты показывают, что оценки, основанные на РРСА, статистически значимо чаще проходят тесты на биномиальность количества исключений, чем оценки на основе РСА, подтверждая преимущество вероятностного подхода в контексте реальных финансовых данных.

В разделе 2 представлены основные понятия и подходы, применяемые в работе. Раздел 3 содержит описание используемых данных, а также описание алгоритмов, процесса их обучения и процесса выбора оптимального окна. Псевдокод реализации алгоритмов приведен в разделе 4. Результаты экспериментов с РСА и РРСА для оценки VaR на различных исходных данных и портфелях рассмотрены в разделе 5. В заключении приводятся основные выводы, сделанные в работе.

Классической мерой риска, используемой Базельским комитетом (см. [22]) для расчета риска, является VaR уровня а, который показывает, что убытки компании будут больше значения VaR_a с вероятностью не более чем а. Формально VaR_a определяется так.

Определение 1. Пусть а G (0,1), X — случайная величина. Тогда

VaRa(X) = -qa(X), где qa(X) = inf{x G R : P(X < x) > a}.

Основная идея данного метода понижения размерности заключается в поиске q-мерной гиперплоскости в d-мерном пространстве, проекция исходных данных на которую обладает максимальной дисперсией (см. [23,24]). Эта задача эквивалентна следующей: в R найти подпространство

Q = {x G R : x = xo + ЖД fi G R9, xo G Rd}, где фактически Ж матрица, размера, d х q. сто.тбпы которой — ото новый q-мерный базис, а d координаты в этом базисе. Подпространство Q размерности q должно наилучшим образом аппроксимировать исходные данные X, т.е. минимизировать по xo и Ж величину

1 ^п

• - £||X -Рr_Q(V)H²,

• ^— i=1

где Pr Q(Xi) — это проекция вектора Xi на подпространство Q.

Данную задачу можно свести к задаче максимизации Ж ^т УЖ м max, при этом Ж ^тЖ = I_q, У = ¹ (X — xo)^T(X — xo) — ковариационная матрица, i I_q~ единичная матрица размера q х q. Решением последней задачи является xo = П S1=1 xi; ^т-^е- эмпирическое среднее по выборке, а также векторы Ж = [w1, ... ,w_q ], составляющие матрицу Ж размера d х q, — это q собственных векторов матрицы ковариаций У. соответствующнх q наибольшим собственным значениям, которые образуют ортонормированный базис.

Заметим, что РСА решает полную задачу понижения размерности:

• •    x G R^d, h(x) = Ж^т(x — x) G R^q,

• •    у G R^q, g(y) = Жу + x G R^.

2.3.    РРСА

Поэтому PCA позволяет решать задачу оптимизации портфеля, содержащего большое количество активов. Для этого сначала применяется РСА и выделяются, например, три независимые компоненты, которые достаточно хорошо позволяют оценивать VaR портфеля. После этого портфель оптимизируется в трехмерном пространстве. Из найденного оптимального трехмерного портфеля обратным преобразованием получается оптимальный портфель исходной размерности.

Главное отличие данного метода от РСА заключается в том, что в нем закладывается вероятностная модель для исходных данных. Probabilistic РСА был представлен К. Бишопом и М. Типпингом в 1999 г. в статье [18].

х — х = Wy + е, где х — среднее по выборке, a W — матрица, размера, d х q.

По выборке X = {хi }”₌₁ необходимо оценить параметры (W, а), максимизирующие правдоподобие модели. Далее будем считать, что данные X центрированы, т.е. х = 0.

В этой модели условное распределение х:

х|у - V(Wy,a2Id), а безусловное распределение:

х -V(0,С), где С = WWт + a2Id. Обратно:

у|х — V(М-1Wтх, a2М-1), где М = WTW + a2Iq.

Для оценки параметров (W, а) по выборке X максимизируется логарифм правдоподобия модели с помощью ЕМ-алгоритма, описанного в работе [18]:

nd.           п                1 Д ,

^(X; W,a) = —— log(2^) — — log(det(C)) — — У хтС 1Xi.

Z i=1

Известно, что РРСА более устойчив к пропущенным данным, чем РСА (см. [18]).

2.4.    Статистика Андерсона — Дарлинга

Далее в работе возникает задача проверки совпадения распределений доходностей двух портфелей: исходного и восстановленного из компонент РСА. Гипотеза о совпадении распределений двух выборок проверяется с помощью двустороннего теста Андерсона -Дарлинга. Важное преимущество данного теста в применении к финансам — его чувствительность к различиям в хвостах распределений. В нашем случае сравниваются распределения исходного портфеля и восстановленного по трем компонентам, полученным с помощью РСА. Если тест Андерсона - Дарлинга проходится, то делается вывод, что портфель восстановлен достаточно хорошо.

Пусть X = {хД”=1 и У = {yi}j=i — две выборки, в каждой из которых элементы отсортированы по возрастанию. Положим Z = {zi}^=i, k = m + п, — объединение X и У, упорядоченное по возрастанию элементов.

Определение 2. Статистикой Андерсона - Дарлинга называется величина fe-1

AD =-V nm ^

i =1

(kc_i — mi)²

i(k — i) ,

где c_i = |{х : х G X : х <  Zi}\ ,i = 1,..., k.

Гипотеза, о совпадении распределений, из которых сгенерированы две выборки, отвергается, если значение статистики Андерсона. - Дарлинга превышает критическое значение, которое вычисляется исходя из уровня значимости и размеров выборок.

2.5.    Бэктестинг

После построения оценки для VaR необходимо протестировать ее качество. Для этого применяется бэктестинг, с помощью которого можно проверить, как хорошо приближаются хвосты распределения.

Пусть R(t) t G 1,...,Т,- временной ряд из реальных изменений портфеля, [R_a(t) - оценка значения VaR уровня а в момент времени t.

Определение 3. Обозначим через I_a(t) следующую величину (исключение):

Ia(t) = Ind[R(t) < -VaRa(t)], где Ind — это индикатор.

Если модель хорошо настроена, то количество исключений имеет биномиальное распределение с вероятностью успеха а и количеством экспериментов, равным размеру выборки, за исключением дат, входящих в первое окно (процесс обучения подробнее будет рассмотрен в п. 3.2). Последнее проверяется в работе с помощью двустороннего теста на биноми-альность из библиотеки scipy, который возвращает значение p-value и границы 95%-го и 99%1-го доверительных интервалов.

В данной работе оценка VaR проводилась на нескольких наборах исходных данных и коллекций портфелей (диверсифицированных и слабо диверсифицированных). Для каждого набора данных и для каждой коллекции определяется доля портфелей, на которых оценка VaR прошла тест на биномиальность количества исключений (с помощью оценки p-value и принадлежности 95%1-му и 99%1-му доверительным интервалам).

3.    Применение алгоритмов на реальных данных3.1.    Описание данных

Для практической реализации были взяты данные с американской биржи Nasdaq с 1 января 2005 г. по 1 января 2024 г. Для корректного учета изменений стоимости акций после дивидендных отсечек использовались дневные данные с пометкой Adjusted Closed. После этого были исключены акции, о которых нет информации за весь промежуток времени, в которых присутствует много пропусков или допущены другие явные ошибки. В итоговом наборе остался 221 актив.

Пусть d — количество акций в портфеле, тТ — длина выборки, т.е. количество дней, за которые взяты данные о стоимости каждой из акций. Важно отметить, что работа ведется не с самими стоимостями акций Pi(t), где i — номер акции в портфеле, а с логарифмическими доходностями (log returns) Ri(t) которые выражаются следующим образом:

P(t)

Ri(t)=Vg        _n,t G [2,Т],i G [1,d].

^piV ^— 1)

Важно, что Ri(t) в отличие от Pi(t) являются безразмерными величинами, — это позволяет работать со всеми активами одинаково.

В каждом положении окна при обучении алгоритмов данные внутри окна нормировались стандартным образом. Под нормализацией понимается процесс приведения данных к виду, при котором они имеют среднее значение, равное нулю, и стандартное отклонение, равное единице. Формально, если Ri(t) обозначает логарифмические остатки для i-ro актива в момент времени t, то нормализованное значение R_i(t) вычисляется так:

RiR =

RiR ^— Vi Ci

где Vi — среднее значение R_i(t) за рассматриваемое окно, с с^ — стандартное отклонение Ri(t) за то же окно. Такая нормализация позволяет устранить влияние различных масштабов и волатильности активов, делая их сопоставимыми и облегчая дальнейший анализ.

Далее под весами портфеля w = (w1 ,...,Wd ) понимается вектop, размерность d которого совпадает с количеством активов в портфеле. Кроме того, Vi G {1,...,d} : w_i >  Си Еы Wi = 1. Портфель с весами w обозначается через R(w) или просто R.

3.2.    Алгоритм с РСА

Для применения метода РСА необходимо определить минимальное количество компонент, достаточное для восстановления распределения исходного портфеля с приемлемым качеством, и произвести оценку VaR.5% используя только выбранные с помощью РСА компоненты. В качестве размера окна для оценки обучения РСА и оценки VaR подобрано оптимальное значение в 350 дней (см. далее п. 3.3), которое балансирует между исторической значимостью и актуальностью данных.

Выбор количества компонент

Поиск минимального количества компонент РСА осуществляется на исторических данных на окне длиной в 35С первых трейдинговых дней выборки. Рассматривался диверсифицированный средневзвешенный портфель, т.е. все 221 акция брались с одинаковыми весами.

Эксперименты показали, что первые три компоненты, найденные РСА, объясняют 47 % дисперсии. График зависимости объясненной дисперсии от количества компонент изображен на рис. 1. Кроме того, по трем компонентам удалось неплохо восстановить распределение исходного портфеля: статистика Андерсона - Дарлинга, посчитанная по значениям исходного портфеля за первые 350 трейдинговых дней и по значениям портфеля, восстановленного из трех компонент, крайне мала (~ С.С15), что не дает отвергнуть гипотезу о совпадении распределений на уровне значимости 5 % (критическое значение ~ 2.49) в отличие от одной и двух компонент.

Таким образом, минимальное количество компонент, при котором нельзя отвергнуть гипотезу о совпадении распределений исходного портфеля и восстановленного по компонентам, равно трем. Это число компонент и используется в дальнейшем исследовании.

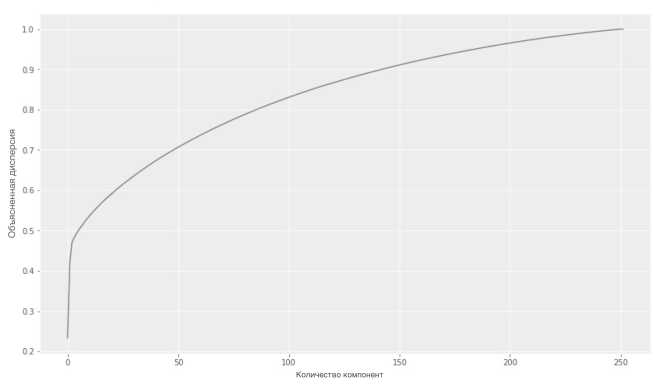
Рис. 1. Объясненная дисперсия в зависимости от количества компонент

Приближение распределения портфеля

После выбора минимального количества компонент для обучения РСА необходимо исследовать, насколько хорошо с помощью РСА приближается распределение портфеля на всех исторических данных, а не только на первом положении временного окна. Для этого окно △ длиной в 350 дней перемещается по всей выборке с единичным шагом, для каждого положения окна △ обучается РСА, по найденным РС1 , РС2 , РСз восстанавливается распределение портфеля и измеряется близость между реальным портфелем и восстановленным. Близость распределений измеряется с помощью статистики Андерсона - Дарлинга.

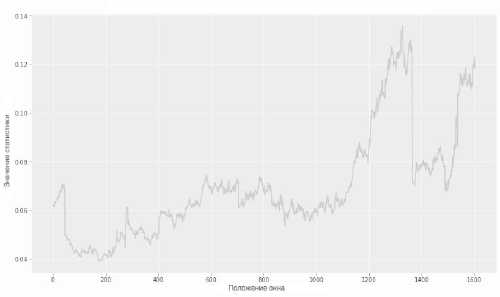
Рис. 2. Значение статистики Андерсона - Дарлинга для исходного портфеля и восстановленного из РС1,РС2,РС3 в зависимости от положения окна

На рисунке 2 изображена зависимость значения статистики Андерсона - Дарлинга от положения окна. Для любого положения окна А гипотезу о совпадении распределений исходного портфеля и восстановленного из РС1, РС₂, РСз отвергнуть нельзя (значения статистики меньше критического значения ~ 2.49).

Оценка VaR по распределению портфеля, восстановленного из трех компонент РСА

Для оценки VaR с помощью РСА на каждом положении окна А обучается РСА, на основе компонент РС1,РС₂,РС3 восстанавливается портфель R_PCa- Оценка VaR_a делается на основе квантили уровня а нормального распределения, оцененного по эмпирическому распределению восстановленного портфеля Rpca • Далее эта оценка сравнивается с настоящим значением портфеля R на следующий день и подсчитывается количество исключений, которые происходят, когда реальное значение портфеля оказывается меньше оценки (см. подробнее п. 2.5).

3.3.    Выбор оптимального окна для оценки VaR с использованием РСА

Для определения оптимального размера временного окна А, используемого при обучении РСА, проводится эксперимент, целью которого является минимизация абсолютной разности между долей исключений и ожидаемым значением а = 5 %. Оптимальное окно обеспечивает наиболее точную оценку VaR5%.

Методика эксперимента. Для оценки качества различных размеров окна выполняются следующие этапы:

• 1)    Размер окна А варьируется в диапазоне от 50 до 1000 трейдинговых дней с шагом 50 дней.

• 2)    Для каждого размера окна А скользящее окно перемещается по временным рядам с единичным шагом, и для каждого положения окна

• •    обучается модель РСА с тремя компонентами, с помощью которых восстанавливается портфель 1?рса:

• •    оценивается VaR₅% на основе нормального распределения восстановленного портфеля;

• •    подсчитывается количество исключений Е_а = |{t : R(t) < -VaR5%(t)}l.

• 3)    Для каждого размера окна вычисляются доля исключений — и абсолютная разность с а = 5 %.

3.4.    Алгоритм с РРСА

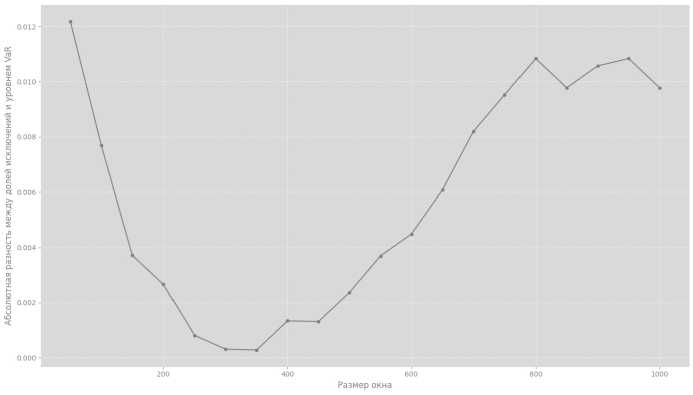
Рис. 3. Зависимость абсолютной разности между долей исключений и уровнем VaR от размера окна △

Критерий выбора. Оптимальное окно △ * выбирается так, чтобы минимизировать абсолютную разность доли исключений и а:

△ * = arg min —— — а . △ п

Результаты эксперимента. Наилучшие результаты достигаются при размере окна △ * = 350 трейдинговых дней, для которого абсолютная разность между долей исключений и а минимальна. На рисунке 3 представлена зависимость абсолютной разности от размера окна, иллюстрирующая выбор оптимального значения.

Таким образом, выбор окна размером △ * = 350 обеспечивает наиболее точную оценку VaR5% для портфеля, восстанавливаемого с помощью метода PC А.

Для применения метода РРСА также используется временное окно △ в 350 дней.

Как и в алгоритме с РСА, окно △ перемещается по всей выборке с единичным шагом, и для каждого положения окна △ РРСА обучается с помощью метода максимизации правдоподобия. Для обучения используется ЕМ-алгоритм, описанный в статье [18].

Таким образом, после обучения РРСА для каждого положения i ок на △ имеются параметры, выученные РРСА: цд Wi, &i. Соответственно модель данных в окне i

Л (m,Wi WT + а21 ).

Примечание. На практике важно учитывать тот факт, что для каждого окна данные были нормализованы (см. п. 3.1).

Имея для каждого окна модель данных, полученную с помощью РРСА, можно оценить VaR уже для конкретного портфеля с весами w. Для этого достаточно получить распределение портфеля. Так как исходные многомерные данные в нашем случае описываются нормальным распределением, то и распределение конкретного портфеля будет одномерным нормальным. Параметры этого одномерного нормального распределения следующие:

Mi (w) = ц wT, a2(w) = w(Wi WT + a21 )wT, где ц(w) — математическое ожидание портфеля с весами w, a a2(w) — его дисперсия. Наконец, для оценки VaR5%0 достаточно посчитать 5 %-ю квантиль полученного одно мерного распределения.

4.    Псевдокод реализации РРСА и его обучения на окнах4.1.    Описание алгоритма РРСА

РРСА основывается на вероятностной модели, где данные представляются как сумма проекции латентных переменных на базис и случайного шума. Для оценки параметров модели используется ЕМ-алгоритм.

Алгоритм 1 Обучение РРСА с помощью ЕМ-алгоритма

Вход: Матрица данных А 6 R"*^ (нормализованная), количество компонент q.

Выход: Матрица компонент W, дисперсия шума с².

Шаг. Оценка среднего значения. Вычислить среднее значение данных:

Д =

Xi.

W =

Е ^Xi^E[ y ^{T |Х}^ ^Е E^F| x i ^]^

С

=Е р i=1

— 2E[ y ^T | x i] W ^T Xi + trace p^T W E[ y i y ^T | x i]

Шаг. Вычисление логарифма правдоподобия:

Lk = — — \d 1п(2л) + In IC| + trace(C-1S)], где C = WWT + 021, aS — ковариационная матрица данных.

Комментарий. Условие завершения — разница между соседними значениями логарифма правдоподобия меньше е.

Конец цикла while.

Вывод W. а².

4.2.    Обучение РРСА на скользящих окнах

Для оценки VaR с использованием РРСА на финансовых временных рядах используется скользящее окно.

Алгоритм 2 Оценка VaR с помощью РРСА на скользящих окнах

Вход: Временной ряд доходностей R(t), длина окна А, параметры модели (q, а).

Выход: Список оттенок VaR_t для каждого псложения окна t.

For t = А То Т

Шаг. Сформировать подвыборку X_t = {R(t — А + 1),..., R(t)}.

Шаг. Вычислить среднее значение p_t и центрировать данные X_t.

Шаг. Обучить РРСА (алгоритм 1) на X_t, получить W, а².

Шаг. Вычислить распределение восстановленного портфеля V(pt,a2), где pt = pWт w, а2 = wT (WWт + о21 )w.

Комментарий. Использование окна фиксированной длины А позволяет учитывать только последние данные, что повышает актуальность оценок.

Шаг. Оценить VaR_t как а-квантиль р аспределения V (р^а²).

Конец цикла For.

Вывод: Список оттенок VaR_t для каждого псложения окна t.

Примечание. В каждом положении окна данные должны быть предварительно нормализованы для повышения точности оценки.

Обучение алгоритма РРСА и бэктестинг для каждого положения окна вычислительно затратны. Для ускорения вычислений используется JIT-компиляция python кода, что дает ускорение более чем в 100 раз. Кроме того, при оптимизации функции правдоподобия РРСА в качестве стартовой точки используется оптимальная точка с предыдущего шага.

5.    Результаты и выводы

Сравнение оценок VaR5% было проведено на нескольких наборах исходных данных:

• •    сектор Financials, 35 акций;

• •    сектор Industrials, 35 акций;

• •    сектор Health Саге, 30 акций;

• •    все отобранные акции, 221 акция;

• •    случайные 100 акций из 221.

Для каждого из предложенных наборов данных были рассмотрены два типа наборов портфелей:

• •    слабо диверсифицированные: 200 случайных портфелей с ведущими 1-5 акциями, в которых сосредоточено 90 % весов портфеля, при этом остальные веса случайно распределены между оставшимися акциями;

• •    диверсифицированные: 200 случайных портфелей, где все веса случайным образом распределены между акциями в портфеле.

Результаты сравнения тестов представлены в табл. 1,2. Для каждой комбинации исходных данных и видов портфелей с помощью РСА и РРСА получены оценки VaR%, которые затем тестировались на биномиальность количества исключений с помощью оценки р-value (строка Бин Тест) и с помощью принадлежности доли исключений доверительным интервалам (строки Д.и. 95 %, Д.и. 99 %).

Значение в каждой ячейке соответствует доли портфелей в коллекции, которые прошли указанный тест.

Таблица!

Слабо диверсифицированные портфели

V aR5%	Industrials		Financials		Health Саге		Все акции		100 случайных
	РСА	РРСА	РСА	РРСА	РСА	РРСА	РСА	РРСА	РСА	РРСА
Бин Тест	14 %	91 %	71 %	91 %	4 %	92 %	0 %	78 %	1 %	87 %
Д.и. 95%	14 %	91 %	73 %	91 %	5 %	92 %	0 %	78 %	1 %	87 %
Д.и. 99%	29 %	98 %	81 %	99 %	7 %	96 %	0 %	90 %	4 %	91 %

Т а б л и ц а 2

Диверсифицированные портфели

V aR5%	Industrials		Financials		Health Саге		Все акции		100 случайных
	РСА	РРСА	РСА	РРСА	РСА	РРСА	РСА	РРСА	РСА	РРСА
Бин Тест	100 %	100 %	100 %	100 %	100 %	100 %	100 %	100 %	100 %	100 %
Д.и. 95%	100 %	100 %	100 %	100 %	100 %	100 %	100 %	100 %	100 %	100 %
Д.и. 99%	100 %	100 %	100 %	100 %	100 %	100 %	100 %	100 %	100 %	100 %

РРСА и РСА показали одинаковые результаты на диверсифицированных портфелях (и та и другая модели постоянно проходят бэктестинг). На слабо же диверсифицированных портфелях метод РРСА значительно превосходит РСА в точности оценки VaR^% на всех наборах данных.

В слабо диверсифицированных портфелях наблюдается высокая концентрация весов в небольшой группе активов, что приводит к существенным искажениям при оценке рисковых метрик, включая VaR5%. Стандартный метод РСА, будучи детерминированным методом максимизации объясненной дисперсии, не моделирует шум явно и не предоставляет вероятностной интерпретации полученных компонент. Вследствие этого РСА может недостаточно точно выделять ключевые факторы риска и недостаточно корректно описывать стохастические флуктуации доходностей. Данный недостаток становится критичным, когда доминирующие активы создают выраженную нелинейную структуру хвостов распределения портфеля.

РРСА частично решает эту проблему, рассматривая данные как реализацию вероятностной факторной модели

X = WY + е, где X — центрированные доходности, Y — латентные факторы, а е — изотропный гауссовский шум с параметром 021. Оптимизация параметров W и с2 через максимизацию правдоподобия обеспечивает статистически обоснованную декомпозицию многомерных данных. В отличие от РСА, РРСА не просто ищет проекцию максимальной дисперсии, а фактически оценивает факторную модель, объясняющую структуру ковариации с учетом неопределенности.

Данная вероятностная постановка дает два ключевых преимущества в условиях слабо диверсифицированного портфеля:

• 1)    Выделение устойчивых факторов риска. За счет явного моделирования шума и латентных факторов РРСА отделяет систематическую составляющую изменчивости от случайных флуктуаций.

6. Заключение

В совокупности эти аспекты делают РРСА предпочтительным инструментом при оценке риска в портфелях с высокой концентрацией весов, где стандартные детерминированные методы понижения размерности могут давать систематические погрешности в оценках крайних значений риска.

В данной работе исследованы два алгоритма для оценки Value at Risk ( VaR) портфелей большой размерности: РСА и РРСА. На основе доходностей акций с биржи Nasdaq и индекса S&P 500 за период 2005-2024 гг. были получены оценки VaR с использованием данных методов. Для сравнения эффективностей алгоритмов был проведен комплексный бэктестинг на различных наборах исходных данных и видах портфелей, включающих слабо диверсифицированные и диверсифицированные портфели.

Основные результаты работы заключаются в следующем:

• 1)    Подбор оптимального окна. Подобрано оптимальное окно для оценки VaR₅% с помощью метода РСА.

• 2)    Бэктестинг. Проведенный бэктестинг показал, что оценки VaR₅%, полученные с помощью РРСА, статистически значимо чаще проходят тесты на биномиальность количества исключений, чем оценки, полученные с помощью РСА.

• 3)    Применимость к различным наборам данных. Метод РРСА превосходит РСА в точности оценки VaR^% на слабо диверсифицированных портфелях на всех наборах данных. Для диверсифицированных портфелей РРСА показал себя не хуже РСА.

Таким образом, метод РРСА продемонстрировал большую эффективность и надежность в оценке финансовых рисков по сравнению с традиционным РСА. Данный метод обладает потенциалом снижения частоты исключений и может быть рекомендован для использования в практических задачах оценки VaR.