Оценка влияния геометрии энергодисперсионного рентгеновского флуоресцентного спектрометра на форму спектра при учете многократного рассеяния

Учет многократного взаимодействия первичного излучения с веществом образца и деталями спектрометра представляет собой достаточно сложную задачу при реальной геометрии энергодисперсионных спектрометров с малым расстоянием между источником излучения, образцом и детектором. При таких условиях для корректного описания спектрального распределения излучения, попадающего в детектор от образца и от элементов спектрометра, требуется детальное рассмотрение процессов когерентного и некогерентного рассеяния. Возникающие задачи оказываются аналогичными при возбуждении рентгеновской флуоресценции излучением рентгеновской трубки и при использовании для этих целей радиоактивных источников, например 109Cd или 241Am.

Рис. 1. К расчету геометрического фактора аналитическим методом [1].

а — модель спектрометра, б — углы падения первичного и отбора флуоресцентного излучений

Модель радиационного переноса с помощью решения транспортного уравнения, предложенная, например, в работе [2], предполагает взаимодействия излучения с веществом, с удаленными от образца источниками излучения и детектором, при которых девиация угла рассеяния пренебрежимо мала.

В статье [1] предложена модель энергодисперсионного спектрометра, которая учитывает разброс углов взаимодействия в системе источ-ник—образец—детектор, однако в такой модели не учитывается процесс многократного рассеяния фотона.

Целью настоящей работы является учет многократного рассеяния первичного излучения в энергодисперсионном спектрометре при малых расстояниях между основными его элементами: источником излучения, образцом и полупроводниковым детектором. При моделировании поведения рассматриваемой системы использован метод Монте-Карло. Результаты расчетов сопоставлены с данными, полученными в работе [1].

ТЕОРИЯ

В работе [1] предложена модель спектрометра с радиоизотопным источником (рис. 1), в которой рентгеновский фотон, с энергией E ₀ покидающий поверхность источника площадью S _source в точке r₀ , попадает на поверхность образца площадью S sample под углом ϕ к его поверхности, проникая в глубину его рабочего объема и взаимодействуя с его веществом в точке r₁ . После взаимодействия фотон, имеющий энергию E , покидает поверхность образца под углом ψ в направлении детектора и попадает в точку r₃ его поверхности площадью S _det . В первом приближении считается, что точка выхода фотона с поверхности образца r₃ совпадает с точкой r₂ попадания первичного фотона. Энергетический спектр с учетом допущения, что |r1 2 - r₃| и |r₀ - r₁₂| меняются слабо, может быть описан в следующем виде для данного процесса взаимодействия:

d N dete ctor d E

const

' ц(E о ) ₊ ц ( E ) ^ , ^sin( ^ эфф ⁾ =И^ эфф ) J

X

J K ( E о ^ E , 0 ) 0

d G ( 0 ) d 0

• d 0 ,

где K ( E 0 ^ E , 0 ) — вероятность преобразования первичного фотона с энергией E ₀ в веществе детектора в E с углом рассеяния 0 между векто-d G ( 0 )

рами г, - Г12 и Г12 - Г3 ; ——--геометриче-_d0

ский фактор, который можно интерпретировать как вероятность наблюдения события при угле однократного рассеяния 0 в заданной геометрии.

Согласно работе [1], были произведены геометрические расчеты геометрического фактора d G ( 0 )

, на основании которого корректировался d 0

расчетный спектр рентгеновского излучения с использованием выражения (1).

В рамках данной работы для учета процессов многократного взаимодействия предложен иной подход к расчету геометрического фактора и спектра излучения, основанный на моделировании процессов в системе источник—образец— детектор по методу Монте-Карло.

Процесс моделирования разбит на три основных этапа:

• •    моделирование источника первичного излучения;

• •    моделирование процессов переноса внутри образца;

• • моделирование процессов взаимодействия флуоресцентного и рассеянного излучений образца с веществом детектора и корректировка спектра функцией отклика детектора.

Геометрическая модель спектрометра при этом полностью аналогична представленной на рис. 1:

– образец — представляет собой цилиндрическое тело с высотой h и радиусом R , расположенное так, чтобы плоскость верхней грани, а также его ось симметрии проходили через точку начала координат (0, 0, 0);

– источник — кольцо с внутренним радиусом R 1 , внешним радиусом R 2 и некоторой высотой h ring , расположенный на удалении D от поверхности образца;

– детектор в виде цилиндра с радиусом R 1 и высотой h ring , расположенного внутри кольца источника излучения.

Пространство между детектором, источником и образцом заполнено воздухом, находящимся под таким давлением, при котором длина свободного пробега фотона в данном объеме в интересующем нас диапазоне энергий была много большей, чем расстояние D между детектором и образцом.

Согласно предлагаемой модели, рентгеновский фотон, возникающий в объеме источника излучения, покидает его поверхность в направлении некоторого вектора r₁ , затем фотон попадает

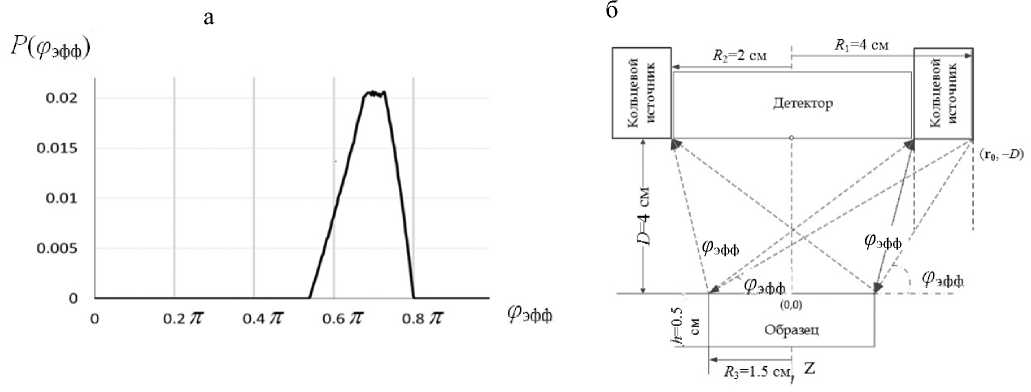
Рис. 2. Моделирование распределения угла падения первичного излучения.

а — функция распределения первичных фотонов P ( φ ), покинувших поверхность источника излучения в направлении образца; б — геометрические пояснения угла φ _э фф

в "рабочий объем" образца. В процессе взаимодействия с веществом образца возникающий флуоресцентный фотон покидает образец из точки r₂ в направлении вектора r ₃ и затем регистрируется детектором.

В качестве основы для расчетов были взяты результаты и модели, представленные в работах [3– 5]. Но предлагаемая модель имеет существенные отличия от них: присутствует моделирование первичного изучения и его пространственное распределение, рассмотрены многократные процессы взаимодействия первичного излучения с веществом образца, а также рассмотрено пространственное и угловое распределения покидающих образец в процессе взаимодействия фотонов.

Для реализации модели кольцевого источника рентгеновского излучения вводятся следующие допущения:

• – в качестве спектрального распределения первичного излучения используется спектр радиоактивного источника ²⁴¹Am, согласно работе [6];

  – излучение первичного фотона происходит непосредственно с его поверхности, направленной в сторону образца, а положение точки возникновения лежит в пределах кольца источника между внутренним радиусом R ₁ и внешним R ₂ .

Следовательно: x = R ₂ - R ₁ ⋅ random ⋅ cos( α ) и y = R ₂ - R ₁ ⋅ random ⋅ sin( α ) — координаты точки возникновения в плоскости XY поверхности источника; α — случайный угол в диапазоне 0 до 2π.

В процессе моделирования производится многократный розыгрыш событий возникновения излучения на поверхности источника, его дальнейшего попадании в образец, взаимодействия с веществом образца и детектирования рассеянного и флуоресцентного излучений, а также точки положения входа на поверхности образца вектора r₁ и его полярного, а также азимутального углов. Результатом моделирования будет распределение угла падения ϕ , функция распределения которого представлена на рис. 2, а.

Попавший в активный объем образца рентгеновский фотон взаимодействует с веществом, при этом происходит изменение направления его движения, а также потеря энергии в процессе некогерентного рассеивания и флуоресценции. Следует отметить, что в рамках данной работы в первом приближении для упрощения модели расчетов не производится моделирование и расчет вкладов спектра тормозного излучения, возникшего в процессе взаимодействия с электронами вещества.

Вероятности процессов взаимодействия, рассматриваемых в данной работе, описываются следующими выражениями.

• • Вероятность ионизации оболочки i фотоном с энергией E ₀ вещества с атомным номером Z при длине пробега d l будет определяться выражением

d P i = τ i ( E 0 ) ρ d l , (2)

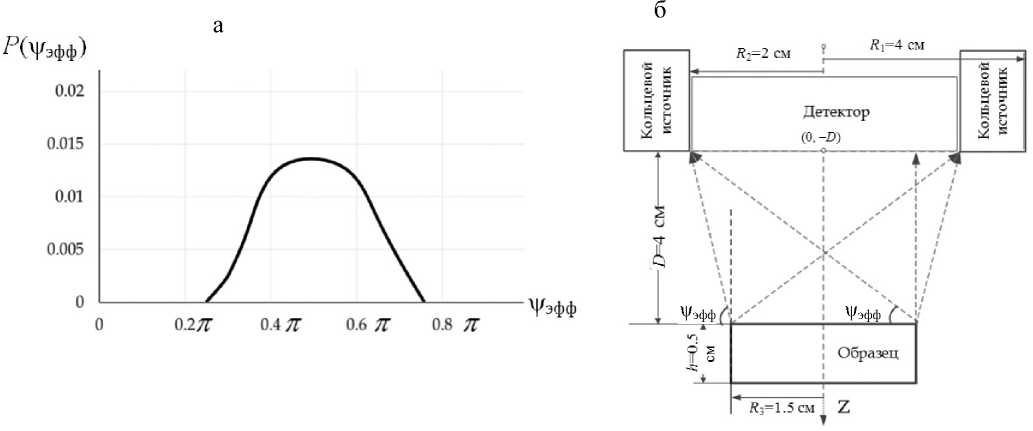
Рис. 3. Моделирование распределения угла отбора детектируемого излучения.

а — угловая функция распределения рассеянных либо флуоресцентных фотонов, покинувших образец и попавших в детектор; б — геометрическое пояснение угла ψ эфф

где τ _i( E ₀) — массовый фотоэлектрический коэффициент поглощения i-оболочкой, ρ — плотность вещества детектора.

• • Для вероятности когерентного рассеяния фотона в веществе детектора на угол θ при длине пробега d l используется уравнение

• ^{d 2 P coh (} θ ⁾ = ρ^{N A} ⋅ ^d σ ^{K (} θ ⁾ ⋅ 2 π ⋅ sin( θ ) ⋅ F ², (3) d θ ⋅ d l A d Ω

где — дифференциальное сечение когерент-dΩ ного рассеяния, определяемое формулой Томсона; F — атомный форм-фактор, определяющий электронную структуру атома.

• Для некогерентного (комптоновского) рассеяния вероятность будет иметь следующий вид:

d² P comp ( E 0 → E ( θ ))

d θ ⋅ d l

= N A ⋅ d σ ^КНТ ( θ ) ρ A   d Θ

⋅ S ,    (4)

где

d σ KНT d Ω

— дифференциальное сечение некоге-

На рис. 3 представлены функции распределения азимутальных углов фотонов, покидающих образец.

На рис. 4 даны результаты расчета геометрического фактора как распределения углов однократного рассеяния в сравнении с результатами работы [1]. Как видно из этого рисунка, модель, рассчитанная аналитическим методом, и модель, полученная моделированием методом Монте-Карло спектрометра, имеют удовлетворительную сходимость.

Представленные на рисунках распределения 2π нормированы на единицу, ∫ P(θ)dθ = 1 , это обу-0

словлено тем, что вероятность сложного процесса (излучение источника—взаимодействие с веществом образца—регистрация) низкая, поэтому в модели рассматриваются отдельно угловые распределения для углов для каждого из этапов моделирования. А результат для распределения угла однократного рассеяния Θ = ψ - ϕ получается математической сверткой распределений

рентного рассеяния, определяемое формулой Клейна—Нишины—Тамма; S — функция некоге-

рентного рассеяния.

Флуоресцентное и / или рассеянное излучение, покидающее активный объем образца, попадает в детектор рентгеновского излучения либо покидает рабочий объем спектрометра.

2 π

P ( Θ ) = P (ψ) ⋅ P ( ϕ ) = ∫ P (ψ - ϕ ) P ( ϕ )d ϕ .    (5)

Для получения спектра регистрируемого сигнала следует анализировать процессы, происходящие в детекторе при поглощении фотона [5, 6].

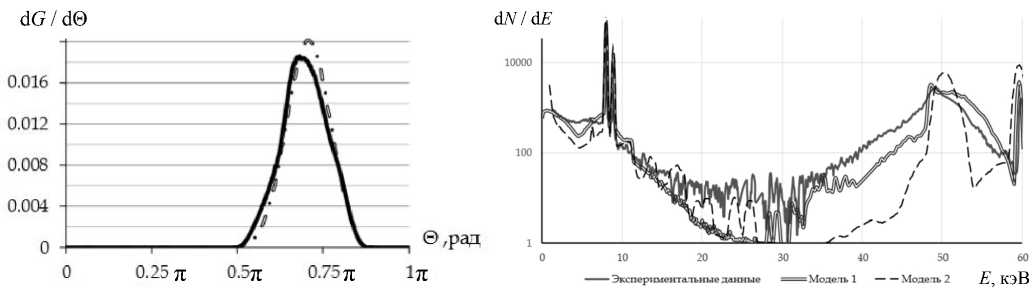
Рис. 4. Функция плотности вероятности углового распределения P (Θ) для падающего и выходящего из образца излучений.

Расчеты данной работы — штрихпунктирная линия, данные из [1] — жирная линия.

Рис. 5. Сравнение экспериментальных данных с расчетами, выполненными в рамках данной работы (модель 1), и расчетных данных работы [1] (модель 2) (²⁴¹Am, Cu).

Попавшее в детектор излучение может поглотиться веществом активной области детектора полностью в результате единичного взаимодействия или каскада взаимодействий. В случае, если фотон покидает пределы чувствительной области детектора при радиационном либо электронном переносе, соответствующий фотон будет зарегистрирован в "артефактах" функции отклика детектора. Также подобной проблемой является неполный сбор заряда в случае регистрации фотона в приповерхностном слое большой концентрации ловушек в приповерхностной области.

РЕЗУЛЬТАТЫ РАСЧЕТОВ И ОБСУЖДЕНИЕ

Полученные в процессе моделирования спектры излучения, покинувшего образец и зарегистрированного детектором излучения, были скорректированы с учетом функции отклика детектора. На рис. 5 представлены расчетный спектр излучения Cu образца с корректировкой на функцию отклика детектора, использованного в данной работы, расчетный и измеренный спектры работы [1]. Все представленные графики нормированы по максимумам линий CuK α .

В области энергий 48–60 кэВ (где фон обусловлен однократным и двукратным комптоновским рассеянием в образце) следует отметить улучшение точности описания фона в спектре по сравнению с работой [1] за счет включения в рассмотрение двух и более кратных процессов. Погрешность описания спектра в этой области составляет ± 10 %.

В областях энергий менее 48 кэВ фон также обусловлен многократным комптоновским рассеянием в образце, поэтому представленный способ расчета, основанный на Монте-Карло-моде-лировании, также дает лучший результат по срав- нению с работой [1]. Однако в данном случае погрешность описания фона остается достаточно высокой, что может быть связано с неточностями значений дифференциальных сечений рассеяния (см., например, [7]) либо отсутствием учета процесса рассеяния излучения на деталях и элементах спектрометра.

Для энергий от 15 до 40 кэВ разница может достигать порядка, что вероятно связано с неполной информацией о спектре излечения радиоактивного источника ²⁴¹Am (отсутствие учета тормозного излучения α -частиц).

Расхождения экспериментального и расчетного спектра в области малых энергий (до 10 кэВ) можно объяснить неточностью дифференциальных сечений комптоновского рассеяния для моделей флуоресцентного излучения образца, а также возможными допущениями в расчетах функции отклика детектора.

ЗАКЛЮЧЕНИЕ

В рамках данной работы было проведено моделирование влияния геометрического фактора энергодисперсионного спектрометра с учетом многократного рассеяния, которое позволило улучшить согласие экспериментальных и расчетных данных по сравнению с моделями, описывающими только процессы однократного рассеяния. Тем не менее требуются дополнительные уточнения, касающиеся как сечения взаимодействия, так и моделирования взаимодействия с деталями спектрометра.

В настоящий момент практическая значимость данных расчетов невысока, но ее результаты должны помочь в понимании механизмов формирования фонового сигнала и его дальнейшего учета и поиску методов повышения соотношения сигнал / фон.