Оценка влияния конусности корпуса экструдера на закон распределения давления по его длине

Непрерывное и постоянно увеличивающееся производство пищевых и непищевых материалов и повышение объемов необходимой переработки продуктов их утилизации требует увеличения выпуска высокоэффективных экструдеров и соответствующего измельчительного оборудования. Снижение энергоемкости и материалоемкости экструдеров и измельчителей, оптимизация осуществляемых в них процессов, позволяет значительно повысить качество технологической переработки материалов и экономическую эффективность утилизационного производства.

Последнее обстоятельство приобретает в последние годы особенно важное значение для снижения экологической нагрузки и воздействия на окружающую среду. Определяющими параметрами процессов перемещения, деформации, экструзии и резания обрабатываемого сырья и материалов являются: геометрические размеры элементов измельчительного или экструзионного оборудования: шнека, корпуса, ножа; толщина выходной решетки; количество и диаметр отверстий в ней, а также физико-механические, трибологические и теплофизические характеристики материалов. Диффузорная коническая форма корпуса экструдера значительно усложняет описание процесса формирования давления вдоль винтовой линии шнека. Именно указанными особенностями обусловлен упрощенный подход к аналитическому описанию такого сложного процесса в работах [3-5], где рассматриваются либо отдельные технологические зоны измельчителей, либо вводятся грубые допущения.

Существенно усложняет моделирование наличие на внутренней поверхности корпуса волчка буртиков противовращения, исключающих проворачивание сырья и тем самым обеспечивающих поступательное движение материала. Это приводит к необходимости учета одной из особенностей конструкции шнековых устройств - формирования сосредоточенных усилий. Второй особенностью, также не нашедшей в литературе освещения, является учет фактора конусности формы корпуса шнека в виде диффузора.

Целью исследования выбрана оценка влияния конусности корпуса шнековых экструдеров и измельчителей на закон распределения давления по длине конического шнекового канала.

Аналитическое описание и решение поставленной задачи в условиях действия на продукт распределенных тормозящих сил трения и сосредоточенных сил сопротивления движению продукта механических элементов (буртиков противовращения) в настоящее время для шнековых измельчителей с конической формой корпуса отсутствует, что принципиально отличает предлагаемое решение от существующих подходов [6-8].

Определение закона распределения давления продукта вдоль траектории перемещения в условиях тормозящего действия на сырье сил трения со стороны поверхности винтового шнека цилиндрической формы, осуществлено в работах [1, 5, 7].

Математическое моделирование силового воздействия механических элементов противовращения – буртиков или шлицов, выполненных на внутренней поверхности цилиндрического корпуса, с учетом воздействия на перемещаемый продукт в винтовом шнековом канале волчка, аппроксимированных распределенными силами, осуществлено в работе [9].

Задачей данной работы является оценка влияния на форму закона распределения давления вдоль винтовой поверхности шнека его конической формы.

Материалы и методы

В настоящее время корпуса волчков, экструдеров и шнековых транспортирующих машин пищевого назначения и иного шнекового оборудования, предназначенного для непищевых производств, выполняются чаще всего в виде конических диффузоров, внутри которых вращаются винтовые шнеки с переменным шагом [4, 9, 10]. Уменьшение шага в направлении к выходу сырья позволяет уменьшить продольные размеры корпуса и шнека. Рабочие значения давления материала на выходе из шнековых устройств достигают сотен атмосфер [11]. При этом коэффициенты трения скольжения сырья по поверхности конструктивных элементов могут принимать различные значения, изменяясь от 0.015 и менее до 0.9 [12].

В связи с высокой энергоемкостью процесса экструзии и измельчения, корректная аналитическая оценка закона распределения давления вдоль шнекового канала волчка конической формы, в условиях действия распределенных сил трения и сосредоточенных сил механического сопротивления со стороны буртиков противовращения имеет принципиальное значение, являясь объектом исследования.

Действительно, из работы [13] известно, что около 35 % совокупных затрат энергии в измельчителях приходится на долю работы сил трения материала об элементы исполнительных механизмов, которая однозначно определяется величиной внутришнекового давления и законом его изменения по длине винтовой линии шнека. Кроме этого, известный процесс "шлюзования" продукта [14] может быть аналитически корректно смоделирован лишь при известном законе распределения давления вдоль винтовой линии шнека.

Методом исследования выбрано физическое и математическое моделирование процесса распределения давления пищевого сырья вдоль конического корпуса экструдера конической формы в условиях действия распределенных сил трения и сосредоточенных сил механического сопротивления буртиков противовращения, а также аналитическое решение полученного дифференциального уравнения.

Результаты и обсуждение

Физическая модель транспортировки материала вдоль конического шнекового канала выбрана по аналогии с материалами исследований [7, 15, 16]. Формирование поля давления считаем происходящим под действием таких факторов, как тормозящее действие распределенных сил трения о шнековую коническую винтовую поверхность на внешнем контуре, и силы трения о внутреннюю поверхность конического корпуса волчка, а также локальной силы механического сопротивления буртиков противоскольжения.

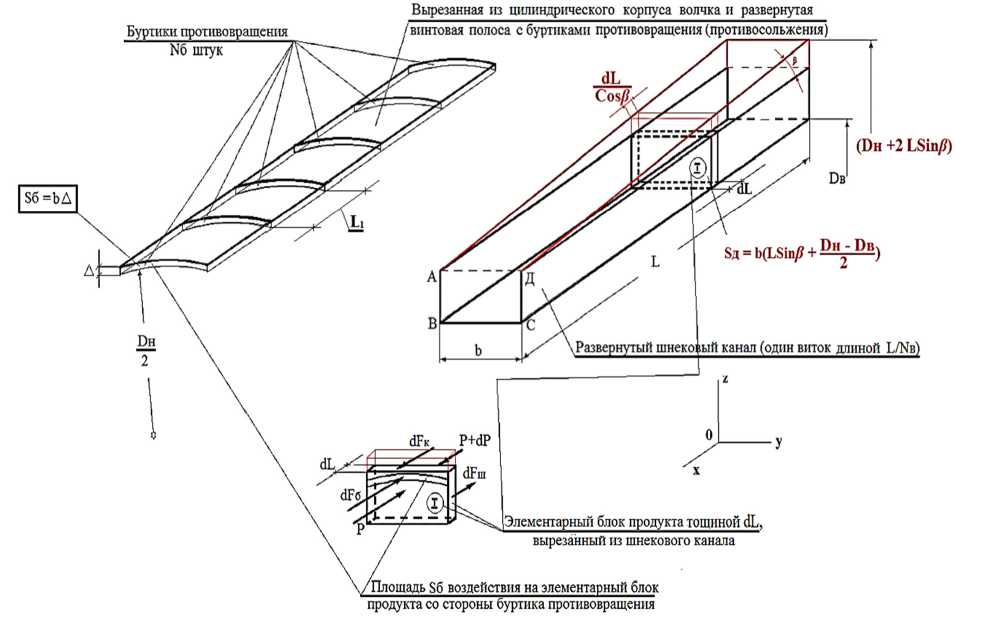
Для корректного решения такой задачи при наличии структурно разнородных силовых факторов (одновременно действующие распределенные и сосредоточенные силы), является использование вместо гидродинамического уравнения Эйлера [17, 18] уравнения равновесия сил (Рис. 1), действующих на элементарный диск толщиной dL, вырезанный из развернутого винтового конического канала шнека, спроектированного на ось OX в дифференциальной форме.

Задача решается ступенчато. На первой этапе, при перемещении сырья на отрезке L 1 (расстояние между соседними буртиками, рис.1), до контакта с площадью первого и последующих буртиков, рассматриваем действие на продукт распределенных сил трения-скольжения.

P+dP

Буртики противовращения

N6 штук Д

Площадь S6 воздействия на элементарный блок продукта со стороны буртика противовращения

Развернутый шнековый канал (один виток длиной L/Nb)

вырезанный из шнекового канала

Вырезанная из цилиндрического корпуса волчка и развернутая

Элементарный блок продукта тощиной dL, винтовая полоса с буртиками противовращения (противосольжения)

(Вн +2 LSin/?)

8д = b(LSin/? + P"₂-^Db)

S6=bA

Рисунок 1 – Физическая модель перемещения продукта в канале конического шнека: L – длина шнекового канала; L 1 – расстояние между соседними буртиками; N в – количество витков шнека; N б – количество буртиков противовращения на внутренней поверхности корпуса волчка; Δ – высота буртика; S б – площадь поперечного сечения буртика; S д – площадь поперечного сечения шнекового канала АВСД; F ш – сила трения, действующая на продукт со стороны поверхности шнека в направлении подачи; F б – сила давления на продукт со стороны буртика противовращения в направлении подачи; F к – сила трения со стороны внутренней поверхности корпуса волчка, действующая на продукт в противоположном направлении

Второй этап обусловлен появлением сосредоточенных сил, действующих последовательно на материал со стороны буртиков противоскольжения в порядке их следования, что отражено топологической схемой развертки внутренней поверхности конического корпуса экструдера, представленной на рисунке 2.

Дифференциальное уравнение равновесия сил в проекции на ось OX запишем в виде:

(9 + dP)Sg - PSg - d] + d] = 0, (1) где: dFm - элементарная сила трения продукта о винтовую поверхность шнека (способствует увеличению давления на выходе), Н; dFK - элементарная сила трения продукта о внутреннюю поверхность корпуса волчка (способствует понижению давления), Н; vд – площадь сечения АВСД пробки продукта в канале шнека, на которую осуществляется давление в процессе перемещения, м2; 9 и (9 + x9) – величины давлений, действующих по разные стороны элементарного диска продукта толщиной dL, Па.

Площадь S д для конического шнека определяется, в соответствии с рисунком 1, соотношением:

y(z н +2|sinÄ-z в )

vд =                      ,         (2)

где y – ширина канала винтового шнека, м;

D н – диаметр наружного цилиндра, образующего выступы шнека, м;

L – текущее значение координаты рас- yd| dvтр.к = ABÇÄ .

Уравнение (1) запишем в преобразованном виде:

v д d9 - d] ш + d] к = 0.         (7)

С учетом соотношений (2) – (6), уравнение (7) примет вид:

y(z н + 2| sin Ä -z в ) d9

-

-

bÅ

9[(y + zн + 2| sin Ä 1-b bÅ yx| zв)d|]+1-b9ÉABÇÄÑ=0.

сматриваемого сечения, м;

β – угол конусности корпуса шнека и

Преобразуем полученное к виду:

волчка, рад;

D в – диаметр внутреннего цилиндра, об-

d9

разующего впадины шнека, м.

Элементарная сила трения dF ш определяется в

соответствии с законом Кулона-Амонтона и с

2Åb y(1 - b)

d|

-

учетом бокового сжатия:

bÅ

x] = ш 1-b

PdS тр.ш^,

где ν – коэффициент Пуассона материала

продукта;

• µ – коэффициент трения скольжения продукта по поверхности шнека;

• xv_тр.ш – элементарная площадь трения рассматриваемой пробки продукта о поверхность шнека, м²;

Элементарная площадь трения о поверхность конического шнека определяется периметром трения (b + Dн – Dв) и толщиной dL пробки продукта в соответствии с выражением: xvтр.ш = (y + zн + 2|ÇkmÄ - zв)d|, (4) где   dL – элементарная толщина пробки про дукта в канале шнека, м.

Элементарная сила d F к трения продукта о внутреннюю поверхность корпуса шнека определяется:

2Åb

(1 - b)ABÇ Ä(z _н + 2| Çkm Ä - z _в )

d|. (8)

Решение уравнения (8) для граничных условий при L = 0, P = P 0 и при L = L 1 , P = P 1 , имеет следующую форму:

*Üá

_{9% = 9&Ö} à((âá) ^{ä (} _×

2 sinÄ ^â*Üá

× [1 +             | % ] ^{çéè*ê((âá)} , (9)

(z_н – z _в )

где P 1 – давление продукта в сечении контакта с площадью первого буртика противовращения, Па;

L 1 – длина пути трения при перемещении продукта до первого (очередного) буртика, м.

Из схемы топологической развертки, приведенной на рисунке 2, следует, что координата L 1 и длина L винтовой линии шнека связаны соотношением:

x] к = _{1 - b} 9dv тр.к .          (5)

Элементарная площадь трения продукта о внутреннюю поверхность корпуса шнека определяется периметром трения, то есть шириной b и толщиной d L пробки продукта. При этом в соответствии с рисунком 1, кривизной поверхности корпуса волчка пренебрегаем:

| = :в:п|%, или

|

^{| % =} : в : п^,

где N в – количество витков в шнеке;

N п – количество заходов ребер противовращения, выполненных на внутренней поверхности корпуса волчка.

Количество пересечений винтового канала и буртиков в соответствии с рисунком 2 составляет величину N б = N в N п .

Во второй фазе, обусловленной появлением сосредоточенной силы со стороны буртика противоскольжения, ориентированного углами наклона винтовой линии шнека γ и ребра противоскольжения γ р , устанавливается давление большее величины Р_г на приращение от воздействия первого буртика на продукт:

Р (1+) = Р % + ^{5 б} Д_д Р 1 * sim(Y + ур) =

Р1 $1 + v6/^ * sim(v + УР))- (11) где   P(1+) – давление продукта за первым бур тиком, Па;

S б – площадь давления на буртик, м².

s₆ = УД,         (12)

где ∆ – высота буртика противовращения, м.

С учетом соотношений (2) и (12), а также плана сил Q 1 и Q 2 , действующих на буртик (Рис. 2), уравнение (11) примет вид:

s6„

^Р(1+) = ^Р1 ⁺ v ^Р1 =

Действительно, учитывая, что сосредоточенная сила Q 1 = S д P 1 , и так как Q 2 = S б P 1 является дополнительной силой, действующей на продукт со стороны первого буртика, то приращение давления от его воздействия определяется отношением этой силы к полной площади сечения пробки продукта с учетом взаимной координации углов наклона винтовой линии шнека γ и ребра буртика γ р (рис. 2).

Таким образом, сразу за первым буртиком, с учетом выражения (9), (10) и (13), установится давление, определяемое соотношением:

2ЦУ

Р (1+) = Р o e ь ⁽ l-v ^{) 1} х

2y.V(COSp-l)

2 sin^ "I Sin2£(1-v)

1+—--^-TL1       х

^(ZH^- z B )

2A * sin(v + vp)

^X[1+    (Zh-Zb)  ^] .     ⁽¹⁴⁾

1-й виток 2-й виток 3-й

4-й виток 5-й виток

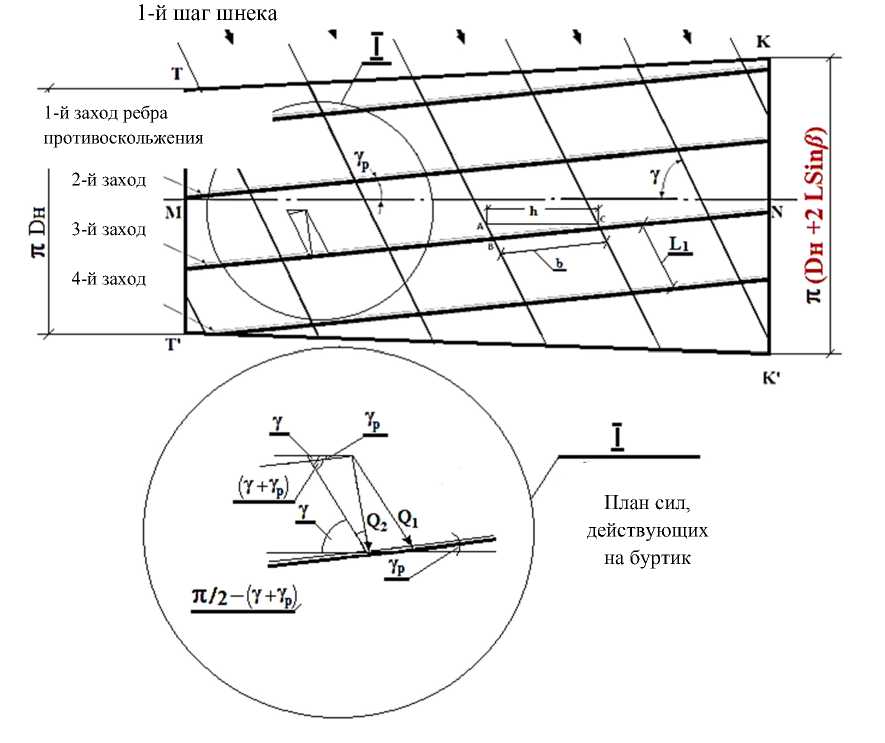
Рисунок 2 – Топологическая схема развертки винтовой поверхности шнека и внутренней поверхности корпуса конического экструдера

На всем протяжении винтовой линии от первого буртика до контакта продукта со вторым буртиком давление P 2 будет расти по экспоненциальной зависимости при начальном давлении не P 0 , а P (1+) , определяемом по аналогичному (9) соотношению:

2ЦУ

9 / = P (%+)^{e b(1-y) 1} x

2 sin^        2p.V(C0S^-1)

x [1 + rn _ n 1 1 ] ^sin2₽(1-v), ^(ZH z_B)

или, после подстановки сюда P (1+) , получаем:

противовращения по длине винтовой линии L получен в виде соотношения (16) и соотношений (17) для давления после очередного буртика с номером « g ».

Результаты расчетов по уравнениям (16) и (17) приведены на рисунке 3.

Исходные данные при этом взяты из реальных прототипов следующие:

ν = 0.43; D = 0.002 м; µ = 0.025; b = 0.03 м; N в = 3; N п = 6; D н = 0.058; D в = 0.026; β = 5^о; γ= 45^о; γ р = 45^о; L = 0.72 м; L 1 = 0.04 м; параметр g принимает последовательные значения от 1 до 18.

2Ц.У

P₂ = P_oe ^bd-y)

2 sin^

x Ii + tk --^1 % !

( ^ZH^{- Z} b )

- 2L

1 _x

2ЦУ(СО5^-1) sin 2^(1-v)

x

x 1 +

2A * sin(y + YP)

(Z h - Z b )

■

Сразу за вторым буртиком, аналогично выражению (13), с учетом (15), установится давление, определяемое соотношением:

2ЦУ

P (2+) = P & e^b(1-y)

- 2L

1 _x

2 sin^

x Ii + tk --^1 % !

( ^ZH^{- Z} b )

2^V(C0S^-1) sin 2£(1-v) x

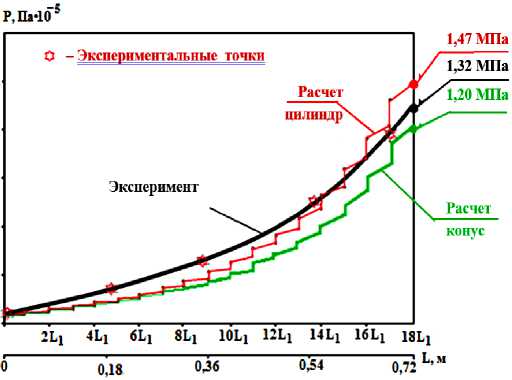
Рисунок 3 – Теоретическая и экспериментальная кривые давления P(L)

x

1 +

2A * sin(Y + ур)] ² (Z h - Z b)    - ■

По изложенной схеме рассуждений, учитывая зависимость (10), можем записать для давления перед буртиком с номером « g » следующую зависимость:

2ЦУ g^1

P₈ = p_oe^b(1-y) «в«п x

2^y(C0S^-1)g

2sin^ I sin2^(1-y) x 1+77;--^1%

-     (^Zh^{- Z} B)    -

x

x |1 +

2A * sin(Y + YP)'

(Z h -Z b )

■](s"°.(16)

Сразу за буртиком с номером « g », учитывая зависимость (10), запишем:

2ЦУ g^1

p₍₈₊₎ = р_ое^ь ( ^1- у)«в«п x

2^V(C0S^-1)g

2sin^ I sin2^(1-y) x 1+77--^1%

-     (^Zh^{- Z} B)    -

x

x 1 +

2A * sin(Y + YP)1 ⁸

(Z h - Z b )

■(17)

Закон распределения внутришнекового давления перед очередным буртиком

Заключение

В результате теоретических исследований и проведенной серии натурных испытаний получены аналитические уравнения (16), (17) и графики зависимости давления экструдируемого материала от длины винтовой линии шнека. По материалам экспериментальных измерений максимальное значение давления на выходе экструдера цилиндрической формы достигает P max = 1.32 МПа.

Рассчитанное максимальное давление для экструдера цилиндрической формы составило P цил.max = 1.47 МПа.

Максимальное давление, рассчитанное для экструдера конической формы при угле конусности β = 5^о уменьшается до значения P кон.max = 1.20 МПа.

Снижение выходного давления в шнековом механизме составило 18.4%, что весьма существенно и должно учитываться при расчете и конструировании экструдеров, волчков, мясорубок и другого шнекового оборудования.

На рисунке 3 приведены графики теоретической и экспериментальной кривых

распределения давления в экструдируемом сырье по длине шнека.

Обработка результатов экспериментов статистическими методами и сравнение с теоретическими данными показали, что отклонение опытных данных от расчетных с доверительной вероятностью 95% не превышает 12%.

Таким образом, разработанная математическая модель закона распределения давления сырья по длине шнекового канала измельчителя в зависимости от параметров экструдера и измельчаемого материала, учитывающая коническую форму корпуса экструдера представляется корректной.

Из анализа полученного закона (17) распределения давления по длине винтовой линии шнека и корпуса экструдера следует, что существенное влияние на скачки давления оказывают углы γ и γ р , то есть взаимная координация направлений витков шнека и ребер буртиков противовращения.