Оценка влияния податливости подложки на напряжения, вызывающие потерю устойчивости отслоившегося покрытия

Интерес к изучению эффектов, связанных с отслоением покрытий, вызывается важностью данной задачи, имеющей приложения в микро- и наноэлектронике, биологии и других областях. Вопросам отслоения покрытий и потери устойчивости посвящено большое количество работ, например [1–8], обзоры можно найти в [6, 8]. Так, в работе [3], в частности, решена задача потери устойчивости отслоившегося участка покрытия в случае жесткой подложки с прямолинейной поверхностью. Найдено критическое

напряжение потери устойчивости, величина выпучивания, скорости высвобождения энергии вдоль и поперек фронта распространения отслоения, а также коэффициенты интенсивности напряжений K_I и K_II на границе отслоения. Отслоившийся участок рассматривался в виде защемленной по краям пластины. Данные граничные условия соответствуют жестким подложкам. Однако детальные исследования показывают, что, с одной стороны, условия жесткой заделки не выполняются точно даже для абсолютно жестких подложек [5], а с другой стороны, на основании результатов численного счета утверждается [6, 8], что даже для подложек, в три раза более мягких по сравнению с покрытием, приближение жесткой заделки дает не слишком заметную ошибку. К последнему утверждению, по нашему мнению, следует относиться с осторожностью, поскольку в [6] не исследовалось влияние длины отслоения, существенность которого подтверждается результатами других работ [5, 9].

Влияние жесткости подложки изучалось в [4–6]. При этом в [4, 6] взаимосвязь относительной жесткости подложки с параметрами отслоения (напряжением потери устойчивости, величиной выпучивания) устанавливалась без учета влияния на эти параметры ширины отслоения. В [5] проводился анализ совместного влияния относительной жесткости подложки и отношения ширины отслоения к ее толщине на величину напряжения потери устойчивости. Отслоение по-прежнему моделировалось участком пластины, для которой граничные условия записывались как условия обобщенной упругой заделки, то есть величины производной прогиба и тангенциального смещения в точке заделки считались пропорциональными продольной силе и изгибающему моменту, действующим в точке заделки. Сами же коэффициенты упругой заделки, зависящие от двух названных параметров, находились путем численного решения системы интегральных уравнений [10].

В настоящей работе рассматриваются модели, описывающие процесс потери устойчивости участком отслоившегося покрытия, предложенные в [9]. В основе моделей, подобно [3, 5], лежит представление отслоившегося участка покрытия как двумерной пластины в рамках классической теории изгиба тонких пластин. Граничные условия записываются не в виде условия жесткого защемления, а в виде либо условий упругой заделки, либо полагается, что пластина покоится на упругом основании. Однако, в отличие от [5], в настоящей работе предпринимается попытка определить коэффициенты заделки аналитически либо полуаналитически на основе модельных представлений. При этом в рамках рассматриваемых моделей, оправданных для широкого диапазона параметров (упругих констант покрытия и подложки и отношения длины отслоения к толщине покрытия), отличие величины критического напряжения от соответствующей величины для жестко защемленной пластины определяется единым безразмерным параметром, представляющим собой комбинацию указанных параметров.

В предлагаемой вниманию работе не рассматриваются вопросы, связанные с процессом дальнейшего отслоения, а также с определением величины выпучивания отслоившейся зоны. Это — предмет последующих самостоятельных исследований. Некоторые оценки величины выпучивания отслоившейся зоны сделаны авторами данной работы в [9].

2.    Постановка задачи

Рассмотрим упругую подложку 1, моделируемую полуплоскостью, к границе которой примыкает покрытие 2, представляемое как упругая полоса (пластина) толщиной h с отличающимися от подложки свойствами (Рис. 1, а). Модули Юнга и коэффициенты Пуассона покрытия и подложки, соответственно, — E, ν, Es, νs . Полоса и полуплоскость имеют полный контакт всюду, за исключением участка длиной 2b , вдоль которого произошло отслоение. Система декартовых координат выбрана так, что ось x параллельна границе полуплоскости, а ось y направлена вдоль ее внешней нормали и совпадает с осью симметрии расчетной области. Начало координат лежит в серединном сечении полосы до деформирования. Таким образом, полуплоскость занимает область (y < - h/2), полоса — (- h/2 < y < h/2), отслоение — (-b < x < b, y = -h/2). Нормальные и касательные напряжения на берегах отслоения и на верхней границе полосы y = h/2 равны нулю.

Предполагается, что полоса подвергается действию собственных деформаций растяжения, вследствие которых появляются сжимающие напряжения ст ₀, действующие вдоль пластины. Такое напряженно-деформированное состояние может возникнуть, например, при нагреве рассматриваемой конструкции, если коэффициент теплового расширения материала полосы выше, чем коэффициент теплового расширения материала полуплоскости. При достижении напряжениями ст ₀ некоторого критического значения ст cr система теряет устойчивость, отслоившаяся часть покрытия изгибается, а центр отслоения смещается в направлении оси y относительно своего первоначального положения на величину 5 (Рис. 1, б ). Задача состоит в отыскании критического значения напряжения ст ₀, при котором происходит потеря устойчивости.

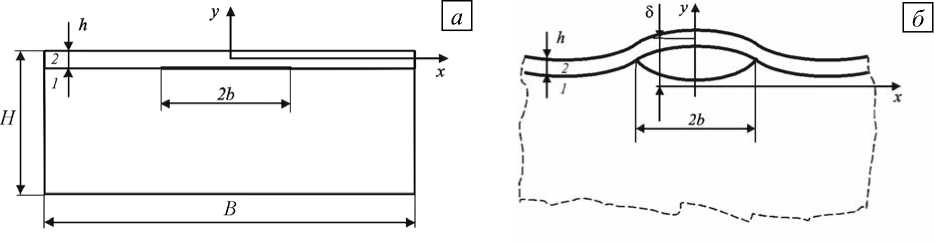
Рис. 1. Геометрия области до ( а ) и после ( б ) деформирования;

1 – полуплоскость (подложка); 2 – полоса (покрытие)

Поставленная задача решалась в работе [6] методом конечных элементов (МКЭ). При этом величина критического напряжения ст cr представлялась как произведение величины ст 0 r , рассчитанной для пластины в условиях жесткой заделки, на некоторый коэффициент у_ст , который и был объектом численного поиска:

cr cr

ст = ст0 Уст .

Величина ст 0 r для пластины длиной 2 b ₀ находится элементарно [11]:

ст 0 r = п ² h² Е У ( 12 b ₀ ² ) ,

Е * = Е / ( 1 -V ² ) .

В настоящей работе поиск коэффициента у_ст осуществлялся на основе соотношений классической теории пластин; рассмотрены два варианта постановки задачи. В первом варианте участок отслоения рассматривался как пластина с граничными условиями типа упругой заделки, во втором — как пластина, опирающаяся на упругое основание.

3.    Модель упругой заделки

Рассмотрим первый вариант задачи, в котором участок отслоения моделируется как пластина с граничными условиями типа упругой заделки (упругого шарнира).

Итак, для участка | x | <  b прогиб пластины u 1 ( x ) , представляющей покрытие, определяется из уравнения

E * h ³/12 u 1 IV ( x ) + с hu 1 ( x ) = 0.                                                         (3)

Здесь с — сжимающее напряжение в сечении пластины, не равное, вообще говоря, с ₀. Отличие с от с ₀ есть результат релаксации, обусловленной искривлением участка пластины и, как следствие, изменением его длины.

Общее решение уравнения (3) имеет вид u1 (x) = Л1 cos kx + A2, |x| < b,(4)

к = ^ 12сcr[^E*h2).(5)

Константы Ai подлежат определению из граничных условий. В точках x = ±b запишем условие упругой заделки u1'( x)| x=b = dhu1( x)| x=b •

Здесь ( d • h ) есть коэффициент пропорциональности между углом наклона в заделке и второй производной от смещения пластины, пропорциональной в свою очередь, действующему в данном сечении моменту; d — безразмерный коэффициент. Появление в условии (6) толщины пластины h вызвано необходимостью согласования размерности его левой и правой частей: толщина — единственный параметр задачи соответствующей размерности (жесткость упругой заделки не может зависеть от размера пластины 2 b , поскольку она является внешним параметром). Подробное обоснование моделей упругой заделки можно найти в [12, 16].

Входящий в условие (6) коэффициент d не может быть определен в рамках элементарной теории пластин. Его выражение получено в работе [18] на основе модели, в которой покрытие рассматривалось как двумерная пластина, а подложка — как полубесконечный упругий массив. Решение найдено при помощи преобразования Фурье и последующего использования метода Винера–Хопфа. Выражение для d есть d = d03E*/E* , где d0 = 22/33-5/6 * 0,636, E* = eJ(1 -v2); E*s = Es Д1 -v2). Подстановка значений производных прогиба (4) в граничное условие (6) дает соотношение tg (kb) + kb • dh/b = 0, откуда для условий жесткой заделки следует, что k = к0 = п/b .(7)

Учитывая (7), а также выражения (1) и (5), получим уравнение для определения у_с :

tg (п7тС) + d оРп7уГ = 0, где в=( hb) VETE*.(9)

Отсюда видно, что отличие критического напряжения, возникающего в рассматриваемой модели, от напряжения, вычисленного при условии абсолютно жесткой заделки, определяется не отдельно упругими и геометрическими параметрами модели, а их комбинацией — единым безразмерным параметром, названным в .

В работе [5] (см. выражения (10)–(17)), на основании модельных представлений, близких к используемым здесь, найдено выражение для критического напряжения потери устойчивости отслоения в неявной форме. Для этого решалась система уравнений, аналогом которых является уравнение (8). Более сложный вид соотношений работы [5] обусловлен использованием ее авторами теории изгиба фон Кармана, по-иному учитывающей вклад продольного сжатия. В указанной работе зависимость коэффициентов системы уравнений (в том числе коэффициента d0в в принятых в данной работе обозначениях) от упругих и геометрических параметров модели определялась путем численного решения системы интегральных уравнений.

Уравнение (8) можно получить из системы уравнений работы [ 5 ], если обнулить в них коэффициент обобщенной упругой заделки, отвечающий за связь угла наклона пластины, моделирующей отслоение, с продольной силой. Можно показать, что влияние этого коэффициента , а, следовательно, и разница между полученным решением и решением из работы [5], уменьшается с увеличением значений bh и EE^s .

Отметим также, что если исходить из асимптотических решений [12–14], найденных для идентичных материалов пластины и подложки из анализа точного решения [15], в которых отслоившееся покрытие не считалось пластиной и учитывались действия как нормальных, так и касательных напряжений, то получим следующее значение коэффициента: d = 0,620 . Разница между значением d , вычисленным согласно данной модели, и асимптотически точным решением составляет менее 3%.

Зависимость у_п от в для пластины с граничными условиями типа упругой заделки представлена на рисунке 2 (кривая 1 ). Как и следовало ожидать, в предельных случаях граничных условий — жесткой заделке ( в ^ 0) и опоры ( в ^ те ), значения у_п стремятся к значениям, отвечающим классическим решениям, соответственно, у_п = 1 и у_п = 1/4 .

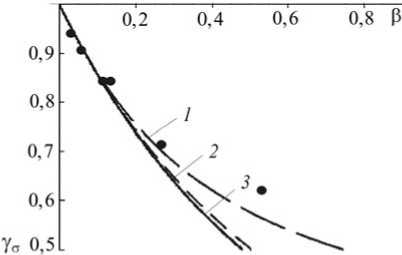
Рис. 2. Зависимость у_п от в :

для пластины с граничными условиями типа «упругая заделка» (кривая 1 ); согласно модели «пластина на упругом основании с учетом влияния сжимающих напряжений» ( 2 ); то же, но без учета влияния сжимающих напряжений ( 3 ); точками показаны результаты численных расчетов

• 4.    Модель пластины на упругом основании

Аналитическое решение поставленной задачи получено в рамках классической теории тонких пластин, согласно которой прогиб пластины, представляющей покрытие, удовлетворяет уравнению

E* (h3/12)ulV (x) + ^(x)hu"(x) + gu(x) = 0.

Здесь u (x) = u1 (x) для |x| > b ; g — эффективная жесткость упругого основания. На участке |y| < b упругое основание отсутствует (g = 0), продольные напряжения постоянны — о(x) = оcr = const, и общее решение уравнения (10) имеет вид (4), в котором константы Ai подлежат определению из граничных условий.

Для участков, где контакт покрытия с подложкой не нарушен, прогиб находим из решения задачи деформирования полуплоскости с заданным распределением нормальных смещений. При этом величина g оказывается существенно зависящей от характерных расстояний, на которых происходит изменение граничных условий.

Так, для синусоидальных смещений с длиной волны X согласно [7] имеем g =п E /X.                                                           (11)

Здесь величина E_s ^* обуславливается типом граничного условия вдоль линии контакта покрытия с подложкой. Поскольку в строгой постановке задачи граничное условие терпит разрыв (в месте отслоения отсутствуют касательные напряжения, а в месте контакта — скачки горизонтальных смещений) и получение точного аналитического решения едва ли возможно, то для оценок можно использовать крайние случаи: отсутствие либо горизонтальных смещений и ( x ) = 0, либо касательных напряжений вдоль всей нижней границы покрытия. В первом случае значение входящего в (11) приведенного модуля Юнга E * определяется как E* = E s ( 1 - v s )/ [ ( 1 + v s )( 3,4 - v s ) ] . Аналогичное выражение во втором случае отличается от приведенного лишь коэффициентом, зависящим от коэффициента Пуассона материала полуплоскости, и вычисляемым по второй из формул (2). Это выражение и будем использовать в дальнейшем.

Заметим, что задача потери устойчивости системы покрытие–подложка представляет наибольший интерес при напряжениях, не превышающих напряжения глобальной потери устойчивости подобной же системы в отсутствие отслоений. Поэтому в первом приближении для участков | x | >  b пренебрегаем вторым членом в уравнении (10), связанным с действием продольных напряжений (влияние соответствующих поправок будет рассмотрено ниже). В силу симметрии задачи относительно оси ординат рассматриваем только область x >  b . Общее решение уравнения (10), не возрастающее на бесконечности, будет иметь вид:

и 2 ( x ) = A ₃ e ^{-a( x} - ^b ) cos a ( x - b ) + A 4 e ^{-a( x} - ^b ) sin a ( x - b ) , x >  b ,                       (12)

4 a ⁴ = 12 g / ( E * h ³).                                                                     (13)

Константы A_i в выражениях (4) и (12) находим из условий сопряжения смещения и его производных в точке x = b :

u1 (b) = и 2 (b), u1 ( x )| x=b = u 2 ( x )| x=b , u1 ( x )| x=b = u 2 ( x )| x=b , u1 ( x )| x=b = u 2 ( x )| x=b .

Подстановка значений прогиба и его производных, полученных из общих решений (4) и (12), в граничные условия (14) дает систему четырех однородных линейных алгебраических уравнений относительно четырех неизвестных A_i . Нетривиальное решение данной системы существует при равенстве нулю ее определителя. После некоторого упрощения условие равенства нулю определителя системы (14) принимает вид:

tg kb + 2 a kJ ( 2 a ² - k ² ) = 0.                                                          (15)

Поскольку критическое напряжение соответствует началу процесса потери устойчивости, то есть началу искривления пластины в месте отслоения, текущее напряжение a равно начальному напряжению a0. С учетом (1), (5) и (7) перепишем уравнение для определения критического напряжения потери устойчивости (15) как tg (^nav^Ra2a V2 (ab )2 -п2 у° = 0.                               (16)

Формула для эффективной жесткости подложки (11) найдена в предположении периодичности нагрузки. Однако выражение для смещения (12) содержит как периодический, так и непериодический сомножители. Из соображений размерности длина волны 2 п/а периодического множителя и длина волны X связаны между собой. Положив длину волны в (11) равной длине волны периодического множителя (12)

Х = 2 л/ 4/ э g, ( E*h ³) ,

получим из (13) следующее уравнение: 4 а ⁴ = 12 E*_s Д E*h ³) -л/Х = 12 E * Д E*h ³) -а/ 2, откуда а = ( 1/ h ) ^3 E * Д 2 E *). С учетом этого выражения величина 1] ( а b ) , являющаяся единственным параметром в формуле (16), представляется в виде: У ( а b ) = d 1 ( hb ) У E 7 E * = d 1 в , где d 1 = .3/2/3 * 0,874.

Сопоставление решения (16) с решением (8) при стремлении в к нулю (что соответствует увеличению жесткости подложки) показывает, что вычисленное в рамках рассматриваемой модели значение параметра 1] ( а b ) несколько завышено (совпадение решений наблюдалось бы при d 1 = d ₀). Сравнение с результатами численных расчетов работы [5] свидетельствуют о том же (см. далее).

Для приближения значений коэффициентов d ₁ и d ₀ друг к другу введем в выражение для эффективной длины упругой волны поправочный коэффициент k _X и заменим формулу (17) соотношением X = 2 п k _х/ ^3gj ( E*h ³) , после учета которого и выкладок, аналогичных описанным выше, получим:

7 ( а b ) = d ₂ ( h/b ) У E 7 E = d ₂ в ; d ₂ = ^2/3 k X/ ³. (18)

Предположение равенства пространственной частоты абсолютной величине комплексного показателя в (12), то есть корню квадратному из суммы квадратов показателя экспоненты и частоты: 2л/Х = ^2(а2 + а2), приводит к значению kX = 1/72 и дает d2 * 0,778, по-прежнему существенно (на 22%) отличающееся от более точного значения d0 * 0,636.

Для совпадения параметров d ₂ = d 0 необходимо положить k _X = 2/3^3/2 * 0,385.

Подстановка (18) в (16) дает

tg(WyT) + WyTd2₽/[1- n2Yc (d2P)2/2] .

Зависимость y_t от в при условии d ₂ = d 0 представлена на рисунке 2 (кривая 3 ).

5.    Модифицированная модель пластины на упругом основании с учетом сжимающих напряжений

Решение (12) может быть модифицировано с учетом влияния сжимающих напряжений на прогиб пластины в областях ее контакта с подложкой. Так, положив для областей контакта | х | >  b в уравнении (10) т = т ₀, получим вместо (12) решение вида u ₂ ( x ) = A 3 e ^{4 а} - ^k ( x - ^b ) ^cos 74 а ² - k² ( x - b ) Д + A ₄e ^{- 4 а - k} ( x ^{- b} ) ^1/2 sin 74 а ² - k ² ( x - b ) Д , x >  b . Подставив его в граничные условия (14), после упрощения вместо (16) найдем следующее условие существования нетривиального решения:

tg (п7у.)+п7т^V4 (a b )2 -

^Ya/( 2 (« b )2 -^Y.) = 0.

Данное решение не отличается качественно от решения (16). Подстановка (18) в (19) дает tg ( ^пТг 7 ) ^{+ П}7т Г d 2 P • V ⁴ -^ Y . ( d 2 p ) ² /( ² — ^пY . ( d 2 p ) ² ) = °.

Зависимость у . от в при условии d ₂ = d ° для данной модели представлена на рисунке 2 (кривая 2 ).

6.    Асимптотические оценки для критического напряжения

Для случая малого отличия у . от единицы, что соответствует малым в , асимптотическое решение уравнения (8) можно получить, осуществив подстановку JY= 1 1 + a 1 x m + a ₂ x n + — , ^гд^е x = d ° в - Теперь, приравняв нулю коэффициенты при одинаковых степенях x , найдем коэффициенты a ₁, a ₂, а также степени m , n , при которых решение существует. Соответствующее решение имеет вид: у . = 1 - 2 x + 3 x ² + O ( x ³ ) , и тогда окончательное выражение для критического напряжения становится следующим:

о cr = п ' h ² E * ( 1 - 2 d ° в + 3 ( d ° в ) ² + --- )/( 12 b ² ) -

Рассмотрим другой крайний случай — малое отличие у. от 1/4, что соответствует большим в - Для этого осуществим подстановку Уу. = 1/2 + a1 ym + a2yn + a3yp +..., где у = 1/(d°в). Приравняв нулю коэффициенты при одинаковых степенях у, найдем коэффициенты ai , а также степени m,n,..., при которых решение существует, и получим соответствующее решение: у.

= 1/4 + 2/ ( п ² d ° в ) - 4/ п ⁴ ( d ° в ) ² + ( 32/ п ⁶ -8/ ( 3 п ⁴ ))/ ( d ° в ) 3 + ...

С учетом последнего окончательное выражение для критического напряжения приобретает вид:

о ^cr =[п ² h²E •/( 12 b ²)] Г . .

Разложение (2°) формально справедливо для в <<  1, то есть, согласно (9), для E*/E * <<  ( b/h ) 3 (соответствует не слишком мягкой подложке). Разложение (21) формально справедливо для в >>  1, то есть для E*/E * >>  ( b/h ) 3 (мягкая подложка). Однако следует помнить, что применение теории пластин оправдано только в случае b/h >>  1. Следовательно, для справедливости разложения (21) должно выполняться условие E У E s * >> ( b/h ) 3 >>  1, указывающее на то, что подложка должна быть чрезвычайно мягкой.

7.    Численное моделирование

Задача для системы покрытие–подложка решалась также методом конечных элементов (МКЭ) в геометрически нелинейной постановке. Геометрия области соответствовала рисунку 1. Расчеты проводились на регулярных сетках. Расчетная область разбивалась на 19600 8-узловых прямоугольных элементов (всего 59401 узлов) со сгущением сетки вблизи точки отслоения. Жесткий слой покрытия моделировался

20 рядами элементов. Ширина расчетной области B полагалась превосходящей длину отслоения 2 b в 20 раз, высота H — в 100-400 раз превышающей толщину покрытия: H ~ ( 100 ^ 400 ) h . Граничные условия были следующими: отсутствовали смещения на границе x = Bj 2 , y = H - h /2 и касательные напряжения и горизонтальные смещения на оси симметрии ( x = 0), а также нормальные и касательные напряжения на верхней границе y = h /2 и на берегах отслоения. Считалось, что материал покрытия имел ненулевой коэффициент теплового расширения, а материал подложки — нулевой. Таким образом, изменение температуры однозначно связывалось с напряжениями в покрытии. Для каждого отношения толщины покрытия к длине отслоения h 2 b из ряда значений (1/20, 1/40, 1/80) и каждого отношения модуля подложки к модулю покрытия (1/1, 1/100) проводился пошаговый расчет зависимости величины выпучивания от температуры.

На первом шаге расчета, для выведения системы из положения равновесия, к отслоившемуся участку покрытия прикладывалось нормальное напряжение, играющее роль возмущения. На втором шаге задавалась температура, создающая внутреннее напряжение, заведомо превосходящее критическое, и система, благодаря возмущению, переходила в положение, соответствующее потере устойчивости. На третьем шаге

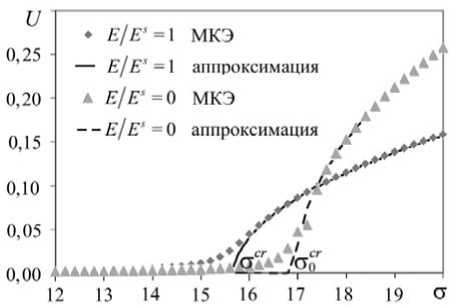
Рис. 3 . Зависимость прогиба от напряжения

принималась за критическое напряжение

возмущающее напряжение снималось, но, поскольку система уже перешла в новое устойчивое состояние, снятие возмущающих напряжений не возвращало ее в исходное невозмущенное состояние. Наконец, на четвертом шаге осуществлялось пошаговое охлаждение, при котором, собственно, и вычислялась зависимость величины выпучивания от температуры. Для напряжений (температур) выше критической величины стcr прогиб аппроксимировался корневой функцией [3] посредством метода наименьших квадратов. Точка пересечения полученной параболы с осью абсцисс стcr. Далее величина уст рассчитывалась как отношение полученного напряжения к критическому напряжению, установленному для случая абсолютно жесткой подложки. Пример данной зависимости для b/h = 80, Е/ Es = 1 и ElEs = 1/100 представлен на рисунке 3.

8.    Выводы

Исследована задача потери устойчивости отслоившегося от подложки покрытия вследствие собственных деформаций сжатия, вызванных, например, нагревом. Предложены аналитические и численные (МКЭ) варианты решения. Модельное аналитическое решение для пластины, которая играла роль покрытия, получено в рамках классической теории тонких пластин. Рассмотрена двумерная задача потери устойчивости сжатой в собственной плоскости пластины, скрепленной с упругой подложкой, которая считалась бесконечным упругим телом всюду, за исключением некоторой области отслоения.