Оценка влияния сроков сева на продуктивность озимой пшеницы методом многомерного дисперсионного анализа

Введение. Выбор сроков сева озимой пшеницы в условиях аридизации климата Орловской области является весьма важным. Это связано с увеличением продолжительности теплого осеннего периода на 2-3 недели со среднесуточной температурой 10-12 ⁰С и часто с недостатком влаги в почве, в сравнении с рекомендуемыми ранее для зоны сроков сева озимой пшеницы. Посев озимой пшеницы в более поздние сроки увеличивает продолжительность периода подготовки поля, что приводит к росту урожайности и благоприятно сказывается на повышении качества зерна. Так, в работе [1] на примере пшеницы сорта Московская 39 показано, что посев в более поздние сроки обеспечил увеличение натуры, накопление белка и клейковины в зерне на 8-24 г/л, 0,7-1,3% соответственно, повышение урожайности на 0,14-0,33 т/га, в сравнении с рекомендуемым сроком.

В цитируемой работе эти выводы сделаны по традиционной методике парного сравнения средних по критерию наименьшей существенной разности (НСР) [2], тогда как при числе сравниваемых вариантов больше двух необходимо использовать критерии множественного сравнения средних, отвечающие методам дисперсионного анализа [3].

На важность применения дисперсионного анализа для принятия обоснованных выводов по результатам биологических исследований указывал А.А. Любищев. Он отмечал, что «одно из огромных преимуществ дисперсионного анализа заключается в том, что он дает возможность проверки правильности модификаций применяемых обработок» [4]. В цитированной работе техника множественных сравнений средних не рассматривалась, однако отмечалось, что даже при значительной разнице между различными вариантами опыта более ценный вывод дает последующая математическая обработка.

В работе [5] на примере исследования по влиянию пробиотика «Олин» на живую массу бройлеров day shift in sowing dates is characterized by a minimum sedimentation value of 31 cm cu. According to the results of the correlation analysis, the yield is positively and strongly correlated with the quality indicators of wheat grain. According to the results of the performed statistical studies, the procedure of a multidimensional generalized linear model is recommended for modeling the influence of agricultural conditions on the yield and quality indicators of wheat grain. Multiple comparison of averages, based on the methods of variance analysis, increases the reliability of statistical conclusions, allows us to identify homogeneous variants of experiments in agricultural production. It is statistically justified that the maximum yield and quality of wheat grain is provided by the sowing period 10 days later than previously recommended for the region.

Учитывая изложенное, выполним с позиций множественного сравнения средних статистический анализ результатов исследований по влиянию сроков сева на качественные показатели зерна озимой пшеницы сорта Московская 39, приведенных в работе [6].

Материалы и методы исследований

В цитируемой работе проводилась сравнение пяти вариантов опытов по схеме таблицы 1.

Таблица 1 – Схема опыта

Вариант	Срок посева
1-й (контроль)	5 сентября
2-й опытный	15 сентября
3-й опытный	25 сентября
4-й опытный	5 октября
5-й опытный	15 октября

В целях получения выводов, не столь жестко завязанных на контрольный срок сева – 5 сентября – введем количественную переменную – сдвиг срока сева, варьирующий от 0 до 40 дней. Исходные данные для моделирования приведены в таблице 2.

Таблица 2 - Эмпирическая база моделирования

Вариант опыта	1	2	3	4	5	НСР05	sx
Срок посева	5.09	15.09	25.09	5.10	15.10	-	-
Сдвиг срока посева, дни	0	10	20	30	40	-	-
Урожайность, ц/га	54,9	58,2	56,3	54,0	47,3	1,4	0,54
Натура, г/л	780	786	805	798	795	6,4	2,47
Белок, %	13,3	14,5	14,0	13,6	12,8	0,33	0,13
Клейковина, %	23,7	25,0	23,5	22,1	19,1	0,9	0,35
Седиментация, см куб.	45	47	39	37	31	3,3	1,27

В таблице 2 приведены средние показатели урожайности и качества зерна пшеницы за три года, тогда как для компьютерной реализации дисперсионного анализа требуются «сырые» данные по годам эксперимента. В работе [6] приведены значения наименьшей существенной разности для всех показателей НСР 05 , что позволяет рассчитать стандартную ошибку опыта s x и выполнить имитацию трехкратной повторности опытов, дополнив множество средних массивами «средние плюс-минус стандартное отклонение».

Результаты и обсуждение

По итогам выполненной нами имитации трехкратной повторности мы располагаем пятью вариантами опытов и данными не только по урожайности, но и по четырем показателям качества зерна пшеницы, и валидным методом выявления влияния на эти показатели сдвига сроков сева является дисперсионный анализ по схеме многомерной обобщенной линейной модели. В рассматриваемом случае многомерный дисперсионный анализ следует предпочесть одномерному, поскольку зависимые переменные коррелируют между собой: согласно корреляционному анализу данных выявлено, что большинство коэффициентов корреляции Пирсона статистически значимы на уровне не хуже 0,05, а учет корреляции зависимых переменных друг с другом позволит учесть все связи, скрытые в числовых данных.

Применение процедуры многомерной обобщенной линейной модели позволяет сравнить между собой варианты опытов одновременно по всем показателям. Проведенные в этой процедуре расчеты подтверждают существенность влияния сдвига сроков посева на урожайность и показатели качества зерна в совокупности.

Важным преимуществом множественных сравнений перед парными по критерию Стьюдента является возможность выделения однородных подгрупп. В данном исследовании применены апостериорные сравнения по критерию Тьюки, результаты которых представлены в таблицах однородных подгрупп и множественных сравнений разностей. Таких таблиц много – пять для однородных подгрупп и пять для множественных сравнений разностей; в качестве примера ниже приводятся таблицы для урожайности.

Таблица 3 - Однородные подгруппы по урожайности (критерий Тьюки, уровень значимости критерия ____________________ различия между подгруппами р =0,05) ____________________

Сдвиг срока сева, дни	Повторность	Урожайность, ц/га (подгруппа)
		1	2	3	4
40	3	47,3
30	3		54,0
0	3		54,9	54,9
20	3			56,3
10	3				58,2
Уровень значимости критерия различия в подгруппе		1,000	0,314	0,060	1,000

Как следует из таблицы 3, варианты сдвига сроков сева на 10 и 40 дней по урожайности зерна образуют самостоятельные подгруппы 1 и 4, при этом урожайность в опыте со сдвигом на 10 дней заметно выше контроля – 58,2 ц/га против 54,9 ц/га, а в опыте со сдвигом на 40 дней – меньше контроля (47,3 ц/га). В то же время, подгруппы 2 и 3 включают в себя контрольный опыт, и отличия урожайности при сдвиге сроков сева на 20 и 30 дней от кон- троля статистически не различимы.

С этими выводами коррелируют результаты множественных сравнений разностей – таблица 4: 95% доверительные интервалы для разностей урожайности при сдвиге сроков сева на 20 и 30 дней включают в себя нуль, что отражает их статистическую незначимость, тогда как разности урожайности при сдвиге сроков сева 10 и 40 дней значимо отличаются от нуля.

Таблица 4 - Апостериорные парные сравнения урожайности по критерию Тьюки

( I ) Сдвиг срока сева, дни	(J) Сдвиг срока сева, дни	Средняя разность (I-J)	Стандартная ошибка	Знач.	95% доверительный интервал
					Нижняя граница	Верхняя граница
0	10	-3,300	0,4409	0,000	-4,751	-1,849
	20	-1,400	0,4409	0,060	-2,851	0,051
	30	0,900	0,4409	0,314	-0,551	2,351
	40	7,600	0,4409	0,000	6,149	9,051

Аналогично, варианты сдвига сроков сева на 10, 20 и 40 дней по содержанию белка образуют самостоятельные подгруппы, при этом содержание белка в опыте со сдвигом на 10 и 20 дней заметно выше контроля – 14,5% и 14,0% соответственно против 13,3% в контроле, а в опыте со сдвигом на 40 дней – меньше контроля (12,8%). В то же время, отличие содержания белка при сдвиге сроков сева на 30 дней от контроля статистически не значимо.

Далее из анализа состава однородных подгрупп следует, что варианты сдвига сроков сева на 10, 20 и 40 дней по содержанию клейковины образуют самостоятельные подгруппы, при этом содержание клейковины в опыте со сдвигом на 10 дней выше контроля – 25,0% соответственно против 23,7% в контроле, а в опыте со сдвигом на 30 и 40 дней – меньше контроля (22,1% и 19,1% соответственно). В то же время, отличие содержания клейковины при сдвиге сроков сева на 20 дней от контроля статистически не значимо.

Выявлено также, что варианты сдвига сроков сева на 20 дней по натуре образуют единственную самостоятельную подгруппу, причем натура в этом опыте выше контроля – 805 г/л против 780 г/л в контроле, а при сдвиге сроков сева на 10 дней натура статистически не отличается от контроля. Еще одна подгруппа объединяет опыты со сдвигом сроков сева на 30 и 40 дней, но в ней натура лишь немного выше контроля.

Последний из зафиксированных в обсуждаемом эксперименте показатель качества зерна пшеницы – седиментация. Из таблицы 5 следует, что вариант сдвига сроков сева на 10 дней по седиментации образуют с контролем общую подгруппу 3, причем показатель 47 см куб. в этом опыте статистически не отличается от контрольного уровня 45 см куб. Подгруппа 2 объединяет опыты со сдвигом сроков посева на 20 и 30 дней, в ней седиментация немного ниже контроля – 39 см куб. и 37 см куб. соответственно. Подгруппа 1 со сдвигом сроков сева на 40 дней характеризуется минимальным значением седиментации – 31 см куб.

Таблица 5 - Однородные подгруппы по седиментации (критерий Тьюки, уровень значимости критерия __________________ различия между подгруппами р =0,05) __________________

Сдвиг срока сева, дни	Повторность	Седиментация, куб. см (подгруппа)
		1	2	3
40	3	31
30	3		37
20	3		39
0	3			45
10	3			47
Уровень значимости критерия различия в подгруппе		1,000	0,363	0,363

С этими выводами коррелируют результаты множественных сравнений разностей, приведенные в таблице 6: 95% доверительный интервал для разности седиментации при сдвиге сроков посева на 10

дней включает в себя нуль, что отражает ее статистическую незначимость, тогда как разности седиментации при сдвиге сроков посева на 20, 30 и 40 дней значимо отличаются от нуля.

Таблица 6 - Апостериорные парные сравнения седиментации по критерию Тьюки

( I ) Сдвиг срока сева, дни	(J) Сдвиг срока сева, дни	Средняя разность (I-J)	Стандартная ошибка	Знач.	95% доверительный интервал
					Нижняя граница	Верхняя граница
0	10	-2,00	1,037	0,363	-5,41	1,41
	20	6,00	1,037	0,001	2,59	9,41
	30	8,00	1,037	0,000	4,59	11,41
	40	14,00	1,037	0,000	10,59	17,41

Важным результатом процедуры обобщенной линейной модели является оценка параметров моделей дисперсионного анализа.

Особенность одномерных моделей дисперсионного анализа в том, что в них каждая переменная представляется в виде суммы среднего значения, эффекта варианта опыта и ошибки. В математической форме однофакторная линейная модель записывается следующим образом:

Yij = µ0 + αi + εi, где Yi – наблюдаемое значение выходной переменной Y на i-м уровне фактора; µ0 – оценка свободного коэффициента модели; αI – оценки главных эффектов на i-м уровне; εi – случайная ошибка.

Интерпретацию параметров моделей дисперсионного анализа поясним на примере линейной модели урожайности (таблица 7).

Таблица 7 – Оценки параметров линейной модели урожайности

Параметр	B	Стд. ошибка	t	Значимость	95% доверительный интервал
					Нижняя граница	Верхняя граница
		Урожайность, ц/га
Свободный член	47,300	0,312	151,715	0,000	46,605	47,995
[сдвиг=0]	7,600	0,441	17,237	0,000	6,618	8,582
[сдвиг=10]	10,900	0,441	24,722	0,000	9,918	11,882
[сдвиг=20]	9,000	0,441	20,412	0,000	8,018	9,982
[сдвиг=30]	6,700	0,441	15,196	0,000	5,718	7,682
[сдвиг=40]	0	.	.	.	.	.

В таблице 7 приведены МНК-оценки параметров модели (1). В ней постоянная µ0=47,3 ц/га, а эффект варианта 5 принят за нулевой, т.е. урожайность зерна пшеницы при сдвиге сроков сева на 40 дней составляет 47,3 ц/га. Эффекты (добавки урожайности) опытных вариантов отсчитываются уже от этого уровня; так, урожайность по опытному варианту 2 (сдвиг сроков сева на 10 дней) характеризуется добавкой α2=10,9 ц/га, с доверительным 95%-ым интервалом (9,9 … 11,9) ц/га, что отвечает урожайности (57,5 … 58,9) ц/га.

Таблица 8 – Оценки параметров линейных моделей показателей качества зерна пшеницы

Параметр	B	Стд. ошибка	t	Значимость	95% доверительный интервал
					Нижняя граница	Верхняя граница
Содержание белка, %
Свободный член	12,800	0,075	170,540	0,000	12,633	12,967
[сдвиг=0]	0,500	0,106	4,711	0,001	0,263	0,737
[сдвиг=10]	1,700	0,106	16,016	0,000	1,463	1,937
[сдвиг=20]	1,200	0,106	11,305	0,000	0,963	1,437
[сдвиг=30]	0,800	0,106	7,537	0,000	0,563	1,037
Содержание клейковины, %
Свободный член	19,100	0,202	94,520	0,000	18,650	19,550
[сдвиг=0]	4,600	0,286	16,097	0,000	3,963	5,237
[сдвиг=10]	5,900	0,286	20,646	0,000	5,263	6,537
[сдвиг=20]	4,400	0,286	15,397	0,000	3,763	5,037
[сдвиг=30]	3,000	0,286	10,498	0,000	2,363	3,637
Натура, г/л
Свободный член	795,000	1,426	557,482	0,000	791,823	798,177
[сдвиг=0]	-15,000	2,017	-7,438	0,000	-19,494	-10,506
[сдвиг=10]	-9,000	2,017	-4,463	0,001	-13,494	-4,506
[сдвиг=20]	10,000	2,017	4,958	0,001	5,506	14,494
[сдвиг=30]	3,000	2,017	1,488	0,168	-1,494	7,494
Седиментация, см куб.
Свободный член	31,000	0,733	42,278	0,000	29,366	32,634
[сдвиг=0]	14,000	1,037	13,501	0,000	11,690	16,310
[сдвиг=10]	16,000	1,037	15,430	0,000	13,690	18,310
[сдвиг=20]	8,000	1,037	7,715	0,000	5,690	10,310
[сдвиг=30]	6,000	1,037	5,786	0,000	3,690	8,310

Высокое качество линейной модели урожайности отражают близкие к нулю значения р -уровня ее параметров (не хуже 0,0005) и близость к единице коэффициента детерминации – 0,986. Последнее означает, что однофакторная линейная модель урожайности объясняет 98,6% общей дисперсии, и только 1,4% дисперсии приходится на другие факторы изменчивости.

Обратимся теперь к моделям показателей качества зерна пшеницы.

Одним из важнейших показателей, определяющих технологические достоинства хлебопекарной пшеницы, является показатель количества и качества клейковины. В опытах по влиянию сдвига сроков сева на качество зерна фиксировали следующие показатели: натуру, содержание белка и клейковины, седиментацию. Для всех этих показателей линейные модели оказались адекватными – коэффициенты де- терминации составили высокие значения от R2=0,951 (натура) до R2=0,968 (содержание белка и седиментация) и R2=0,980 (содержание клейковины).

МНК-оценки параметров моделей показателей качества зерна пшеницы приведены в таблице 8. В этой таблице свободный член моделей отвечает варианту сдвига сроков сева на 40 дней относительно контроля, т.е. эффекты отсчитываются уже от этого уровня.

В двух последних графах приведены 95%-ые доверительные интервалы параметров. Практически все они не включают в себя нуль, что отражает статистическую значимость наблюдаемых эффектов.

Влияние сдвига сроков сева на показатели качества зерна пшеницы можно проследить по диаграммам рисунка 1, сгенерированным в программной среде процедуры «линейная обобщенная модель».

а                                                   б

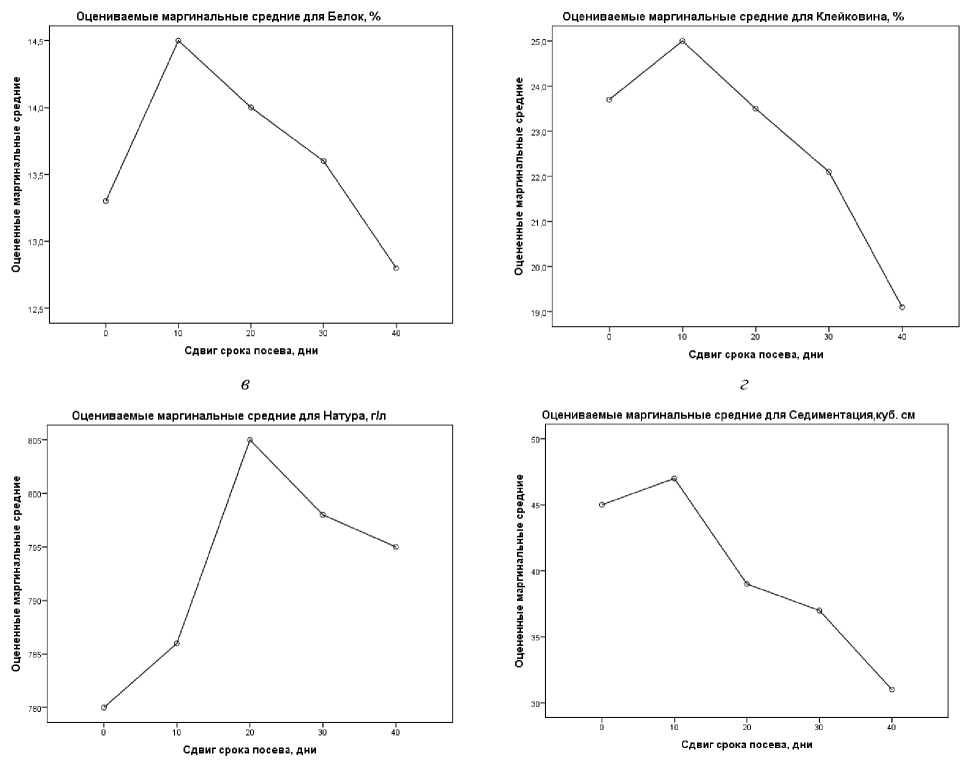
Рис. 1 – Зависимость показателей качества зерна пшеницы от сдвига сроков посева: а – содержание белка; б – содержание клейковины; в – натура; г – седиментация

На этих диаграммах видно, что максимумы всех показателей качества, кроме натуры, приходятся на вариант 2 со сдвигом срока сева относительно контроля на 10 дней. Учитывая, что максимум урожайности также приходится на этот вариант, сдвиг сроков сева пшеницы на 10 дней в сравнении с рекомендуемым ранее, можно считать оптимальным.

Судя по результатам выполненного нами кор- реляционного анализа, урожайность положительно и сильно коррелирует с показателями качества зерна пшеницы.

Кроме того, показатели качества положительно и сильно коррелируют друг с другом, что представляет несомненный интерес объединить их в некий обобщенный показатель качества. В качестве такого показателя целесообразно использовать функцию желательности Харрингтона, нормированную на интервал (0; 1) [8], как это было реализовано в нашей предыдущей работе [1]. В данной работе обобщенная функция желательности Харрингтона была определена по массиву 46 сортов, а затем использована для оценки качества зерна пшеницы сорта Московская 39 в зависимости от сроков сева; при этом оценка «хорошо» и «удовлетворительно» соответствовала сдвигу срока посева на 10-20 дней.

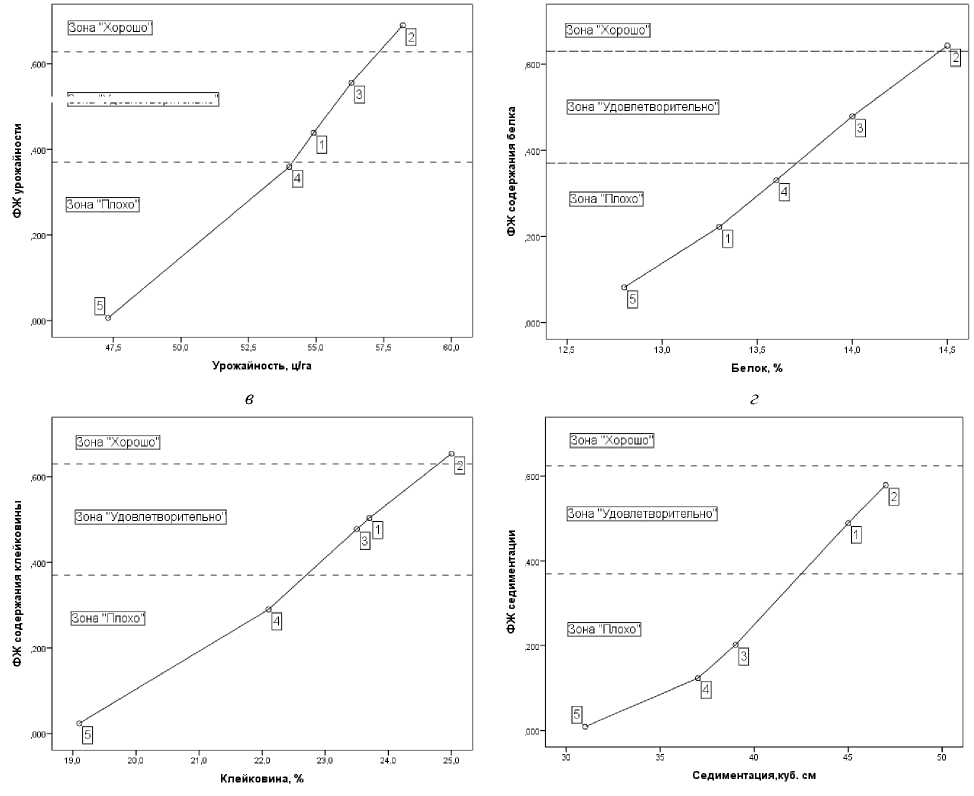
Нами построены частные функции желательности Харрингтона для всех трех показателей качества, помимо этого, строили также функцию желательности для урожайности; согласно методике, изложенной в [13], нижними реперными точками для их построения являлись средние значения показателей по выборке, верхние отстояли от них на величины стандартных отклонений. При таком выборе реперных точек все функции носят характер S -образных кривых - рисунок 2.

б

а

[Зона "Удовпетворительно'1

Рис. 2 - Распределение вариантов опыта по срокам посева (числа вблизи меток) по зонам желательности: а - урожайность; б - содержание белка; в - содержание клейковины; г - седиментация. Пунктирными линиями выделена зона «Удовлетворительно»

Из рисунка 2 следует, что если по урожайности, содержанию клейковины и седиментации результаты контрольного опыта оцениваются как «удовлетворительно», то по содержанию белка - как «плохо». Тогда как сдвиг срока сева на 10 дней «переводит» оценки урожайности и содержания белка, клейковины в зону «хорошо».

Малый объем выборки (пять вариантов опытов) не позволяет корректно выполнить факторный анализ. Тем не менее, применение метода главных компонентов позволило выявить тенденцию, что три частные функции желательности Харрингтона - содержания белка и клейковины и седиментации - мо- гут быть объединены в один главный фактор, объясняющий более 80% общей дисперсии. Это позволяет определить обобщенный показатель качества зерна пшеницы как среднее арифметическое частных функций желательности Харрингтона.

На рисунке 3 представлено распределение вариантов опыта по зонам желательности урожайности и обобщенного показателя качества зерна, в зависимости от сдвига сроков посева. Видно, что максимумы обеих зависимостей приходятся на сдвиг сроков сева на 10 дней позднее рекомендуемых сроков для региона.

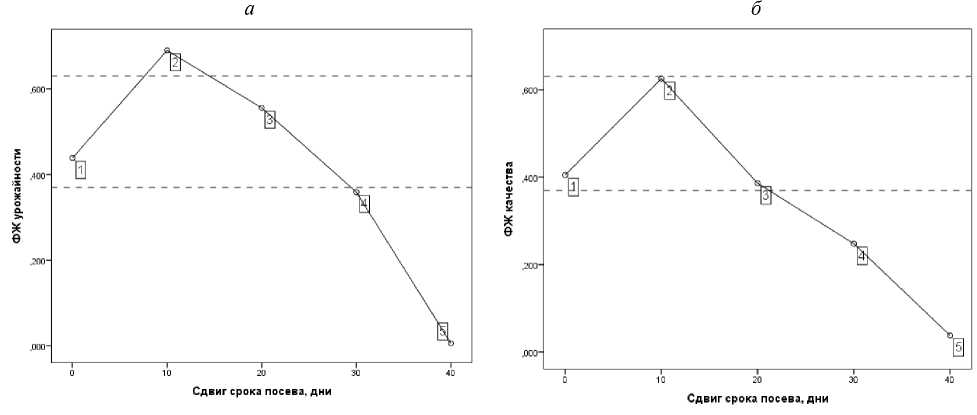
Рис. 3 – Распределение вариантов опыта (числа вблизи меток) по зонам желательности: а – урожайность; б – обобщенный показатель качества зерна. Пунктирными линиями выделена зона

«Удовлетворительно»

Выводы

• 1.    По результатам выполненных статистических исследований процедура многомерной обобщенной линейной модели рекомендуется для моделирования влияния условий агротехники на урожайность и показатели качества зерна пшеницы.

• 2.    Множественное сравнение средних, основанное на методах дисперсионного анализа, повышает

• 3.    Статистически обосновано, что максимумы урожайности и качества зерна пшеницы обеспечивает срок посева на 10 дней позже относительно ранее рекомендуемого для региона.

надежность статистических выводов, позволяет выделить однородные варианты экспериментов в аграрном производстве.