Оценка влияния температуры на физико-технические свойства горных пород

DOI:

e-mail: , ORCID:

Гусак С. А. Оценка влияния температуры на физико-технические свойства горных пород. Вестник МГТУ. 2025. Т. 28, № 1. С. 81–91. DOI:

Apatity Branch of Murmansk Arctic University, Apatity, Murmansk Region, Russia; e-mail: , ORCID:

Gusak, S. A. 2025. Assessment of the effect of temperature on the physical and technical properties of rocks. Vestnik of MSTU, 28(1), pp. 81–91. (In Russ.) DOI:

В течение нескольких лет в Горном институте КНЦ РАН проводились комплексные исследования по обоснованию методологии создания подземных комплексов для захоронения радиоактивных материалов и размещения атомных станций малой мощности в условиях Арктики. Некоторые результаты этих исследований опубликованы в ряде работ (см. например, Мельников и др., 2001; 2010; 2020 ).

Значительное внимание в исследованиях Горного института было уделено тепловому воздействию на вмещающий породный массив, которое может способствовать развитию термомеханических эффектов в ближней зоне подземных объектов. Наряду с параметрами источника тепла существенное влияние на формирование температурного поля в породном массиве оказывают теплофизические свойства горной породы – коэффициент теплопроводности λ , удельная теплоемкость С и плотность ρ . Модуль упругости породы Е и коэффициент линейного теплового расширения β определяют абсолютные значения термических напряжений, формирующихся в породном массиве под влиянием теплового поля. При этом повышенные температуры, которые характеризуют эксплуатационный режим подземного объекта, могут оказывать влияние на параметры физико-технических свойств горной породы.

В настоящей работе выполнена оценка влияния температуры на физико-технические свойства скальных пород на примере гранитоидов, которые залегают в пределах Мурманского блока – одного из наиболее крупных тектонических подразделений Кольского мегаблока северо-восточной части Балтийского кристаллического щита. Осредненные экспериментальные данные, предоставленные Ковалевой Г. А., по минеральному составу и физическим свойствам выбранных типов гранитоидов, приведены в табл. 1 и 2. В табл. 2 в числителе приведены интервалы изменения исследованных свойств, а в знаменателе – их средние значения.

Таблица 1. Средний минеральный состав гранитоидов, вес.% (данные Ковалевой Г. А.) Table 1. Average mineral composition of granitoids, wt.% (data from Kovaleva G. A.)

Порода	Кварц	Плагиоклаз	Микроклин	Биотит	Роговая обманка
Гранодиорит	5	60	15	7	13
Аляскитовый гранит	40	34	25	1	–

Таблица 2. Физические свойства гранитоидов (данные Ковалевой Г. А.) Table 2. Physical properties of granitoids (data from Kovaleva G. A.)

Порода	ρ , г/cм3	Е , ГПа	ν	σ сж , МПа	V p , км/с
Гранодиорит	2,60–2,69 2,65	42–59 50	0,17–0,30 0,22	151–256 183	4,27–5,17 4,69
Аляскитовый гранит	2,55–2,59 2,56	41–59 50	0,17–0,29 0,23	202–329 241	4,59–5,21 4,80

Плотность рассматриваемых горных пород варьируется в достаточно узком интервале значений – от 2,55 до 2,69 г/см3, что при значительных вариациях минерального состава соответствует небольшим различиям в плотности основных породообразующих минералов. Более широкие вариации значений модуля упругости (от 41 до 59 ГПа) обусловлены зависимостью упругих свойств не только от минерального состава, но и от структурных факторов. Различия в прочностных свойствах горных пород также отражают особенности минерального состава и структурных ослаблений. Можно отметить, что аляскитовые граниты, для которых характерно достаточно высокое содержание наиболее прочного кварца и самое низкое содержание темноцветных минералов, а также относительно наименьшее проявление структурных ослаблений, отличаются наибольшей прочностью на сжатие.

Материалы и методы

В оценках параметров физических свойств гранитоидов были приняты параметры свойств породообразующих минералов при нормальных условиях, приведенные в табл. 3.

Таблица 3. Параметры физических свойств породообразующих минералов ( Наука…, 1969; Справочник…, 1975; Беликов и др., 1970; Дмитриев и др., 1969; Физические…, 1984; Horai, 1971 )

Table 3. Parameters of physical properties of rock-forming minerals ( Science…, 1969; Handbook…, 1975;

Belikov et al., 1970; Dmitriev et al., 1969; Physical…, 1984; Horai, 1971 )

Минерал	ρ , г/cм3	λ , Вт/(м·К)	С , Дж/(кг·К)	β ·106, 1/К	Е , ГПа	ν	σ сж , МПа
Кварц	2,66	6,5	740	11,0	96	0,08	400
Плагиоклаз: олигоклаз альбит	2,64 2,61	2,1 2,2	840 730	9,0 7,0	78 73	0,29 0,28	130 110

Микроклин	2,60	2,9	680	5,35 (60 °С)	76	0,29	120
Биотит	2,90	1,1	770	10	69	0,27	–
Роговая обманка	3,10	3,0	700	7,6	105	0,28	94

Для оценки коэффициента теплопроводности гранитоидов использовалась формула логарифмического средневзвешенного, которая рекомендована Ржевским В. В. и Новиком Г. Я. ( Ржевский и др., 1984 ) для пород, представляющих собой статистические смеси минералов:

n

1g ^ = x w-' !g^ ■,                                            (1)

i = 1

где X , X i - теплопроводность породы и i -го минерала соответственно; w i - относительное объемное содержание породообразующих минералов.

Удельная теплоемкость скальной (плотной) породы зависит только от ее минерального состава, и для теоретической оценки теплоемкости использована формула арифметического средневзвешенного ( Ржевский и др., 1984 ):

n

C = Е С^ ' m - ’                                           (2)

i = 1

где m i – относительное массовое содержание породообразующих минералов с удельной теплоемкостью С i .

В работах ( Ржевский и др., 1984; Новик и др., 1994 ) отмечается, что связь между коэффициентом теплового расширения пород и минеральным составом осуществляется не непосредственно, а через произведение параметров теплового расширения минералов и модуля упругости. Для расчета среднего коэффициента линейного теплового расширения р полиминерального агрегата в работе ( Новик и др., 1994 ) рекомендована формула следующего вида:

P = ( E П = i P i - K i- w ) / E n = 1 K i - w - ,                                      (3)

где P i , K i , w i - средний коэффициент линейного теплового расширения, объемный модуль упругости и относительное объемное содержание i -го минерала соответственно.

В формуле (3) взаимосвязь К i и Е i определяется из известного соотношения

K i = E i /(3 - 2 v ),                                               (4)

где v i - коэффициент Пуассона.

Как отмечалось ранее, тепловое воздействие может оказывать влияние на параметры физикотехнических свойств горной породы.

Повышение температуры приводит к усилению взаимодействия ионов в кристаллической решетке вследствие увеличения их колебания. Это явление обусловливает уменьшение величины пути свободного пробега фононов и как следствие этого, снижение теплопроводности многих кристаллических пород и минералов. Такая закономерность в рассматриваемом интервале температур экспериментально установлена, в частности, для скальных пород типа гранита (Дмитриев и др., 1969; Ржевский и др., 1984; Новик и др., 1994; Heuze, 1983; Sibbit et al., 1979). В работе специалистов научной лаборатории Los Alamos (Sibbit et al., 1979) рассматривается построение эмпирической модели теплопроводности гранитов. Отмечается, что для гранитов при фиксированной температуре теплопроводность породы повышалась по мере роста объемного содержания кварца и К-полевого шпата (в нашем случае – микроклина). Поскольку экспериментально установлено, что теплопроводность кварца сильно зависит от температуры, для построения аппроксимирующей зависимости предположили, что температурная зависимость теплопроводности породы определяется кварцевой компонентой в минеральном составе. Используя это предположение, выражение для функции X породы записано в следующем виде (Sibbit et al., 1979):

Ов = W e

₁₊ В ■ (Т о - Т ) ^ Кв ■ ТТ

,   л о        , Ф⁽ w - X

’шп  ^(А шп ^{/ К} кв ) ⁺   , О ) ,

К кв

где X _кв° и X _шп ^о - теплопроводность кварца и К-полевого шпата при нормальных условиях соответственно; В = 2,28 ^ 10 3 Вт/м - температурный коэффициент для X _кв ; w_кв , w_m „ - объемные доли кварца и К-полевого шпата соответственно; ϕ(w _i ) – вклад в теплопроводность породы при нормальных условиях от других минералов.

Следует отметить, что предположение о слабом влиянии других породообразующих минералов на температурную зависимость теплопроводности гранита частично подтверждается теоретическими оценками Юрчака Р. Г. ( 1980 ), согласно которым теплопроводность микроклина, второго после кварца вкладчика в композиционную теплопроводность породы, практически не зависит от температуры.

Для оценки теплопроводности пород, представляющих собой статистические смеси минералов, использована формула логарифмического средневзвешенного (1). На основе предположения о ведущем влиянии кварца на температурную зависимость теплопроводности породы для определения функции X( Т) эта формула может быть записана в следующем виде:

n lgЦТ) = We ■ iglкв (Т) + £ wiglо,                              (6)

i = 1

где w_кв , X _кв ( Т) - объемная доля и температурная зависимость теплопроводности кварца соответственно; w i , X i⁰ - объемная доля и теплопроводность при нормальных условиях других породообразующих минералов.

Для формализованного представления функции X _кв ( Т) были использованы данные, приведенные в справочнике ( Справочник..., 1975 ). При этом применена зависимость, которая представлена в работе ( Sibbit et al., 1979 ) в качестве формы эмпирического закона для гранитов. С учетом справочных данных аппроксимирующая функция для кварца с X кв = 6,5 Вт/(м - К) записывается следующим образом:

X кв ( Т) = 6,95 - 2,31 ■ 10^-2 - Т + 3,66 - 10^-5 - Т ,                                    (7)

где Т - температура, °С.

В отличие от теплопроводности удельная теплоемкость при нагреве повышается, что обусловлено увеличением энергии собственных колебаний частиц в минеральной фазе горной породы. В общем виде температурная зависимость удельной теплоемкости минералов и породы C ( T) может быть записана в следующем виде (Дмитриев и др., 1969 ):

С ( Т ) = А + В • Т - D • Т ².                                     (8)

Для расчета температурной зависимости удельной теплоемкости породы были использованы данные работы ( Дмитриев и др., 1969 ) по изменению теплоемкости основных породообразующих минералов с температурой, которые описываются следующими аппроксимирующими зависимостями в относительном виде:

• -    для кварца

Скв(Т)/Сокв = 1,024 + 8,2 ■ 10-4 ■ T- 2,27-104 ■ Т2;(9)

• -    для микроклина

Смк (Т)/СМ = 1,353 + 2,27 ■ 10-4 ■ T - 3,6 ■ 104 ■ Г2;(10)

• -    для плагиоклаза

Сл (Т)/Ст = 1,338 + 2,46 ■Ю-4 ■ T - 3,52 ■ 104 ■ Т2,(11)

где С ( Т) - удельная теплоемкость при температуре Т , Дж/(крК); С ° - удельная теплоемкость при Т о = 293 К; Т - температура, К.

Кристаллические скальные породы типа гранита отличаются малой пористостью. Поэтому объемная масса таких пород, как и плотность, практически определяются плотностью породообразующих минералов ( Ржевский и др., 1984 ).

Учитывая указанную особенность, можно утверждать, что если при нагреве в породе не происходят фазовые превращения, дегидратация или другие эффекты, вызывающие нарушение структуры минерального скелета, то параметр плотности породы может считаться величиной постоянной. Количественно данное утверждение для пород типа гранита в интервале температуры от 20 до 100 °С подтверждается оценкой температурной зависимости р ( Т) , предложенной в комплексной работе ( Результаты..., 1993 ) на основе обобщения экспериментальной информации по основным типам пород Балтийского щита:

р(р о , Т) = р о -(1 - 2 ■ 10^-5 ■ Т ),                                              (12)

где р _о - плотность породы при нормальных условиях; Т - температура (°С).

Из формулы (12) легко увидеть, что при повышении температуры до 100 °С плотность породы изменяется в пределах 0,2 %.

Модуль упругости Е , характеризующий способность породы сопротивляться деформированию, для большинства кристаллических пород с повышением температуры уменьшается ( Дмитриев и др., 1969; Физические..., 1984; Ямщиков, 1965; Heuze, 1983 и др. ). Теоретическими и экспериментальными исследованиями установлено, что изменение модуля упругости с повышением температуры минералов и мономинеральных пород носит линейный характер ( Наука…, 1969; Дмитриев и др., 1969; Ржевский и др., 1984; Ямщиков, 1965 ) и обусловлено только изменением температуры внутри минералов.

Для большинства полиминеральных пород температурные зависимости модуля упругости имеют отклонения от линейности. Объяснение нелинейного характера изменения модуля упругости таких пород основано на предположении о проявлении релаксационных явлений на границе между минералами, слагающими породу, или в самих минералах (Дмитриев и др., 1969; Ямщиков, 1965). Экспериментально установлено, что начало релаксационных явлений для большинства горных пород наблюдается при температуре 200-300 °С. При этом различное проявление релаксационных явлений обусловливает различия и в характере температурной зависимости модуля упругости. Так, горные породы, для которых отмечаются пластические явления в самих минералах, имеют более резкое отклонение от линейной зависимости по сравнению с породами, для которых такое отклонение объясняется пластическими явлениями на границе между минералами (Дмитриев и др., 1969). К последнему типу пород относятся граниты, для которых характерно заметное снижение модуля упругости с повышением температуры при наибольшем отклонении от линейной зависимости (Ямщиков, 1965).

Для определения температурной зависимости Е ( Т ) воспользуемся формулой, устанавливающей взаимосвязь скорости продольных волн V p и модуля упругости ( Ржевский и др., 1984; Физические…, 1984 ):

V p = JE ( 1 - v ) / |> ( 1 + v ) - ( 1 - 2 v ) ] .                                 (13)

Как отмечалось ранее, для скальных пород типа гранита величина ρ в интервале температуры (от 20 до 100 °С) может считаться постоянной. Изменение коэффициента Пуассона ν гранитов под влиянием теплового поля не имеет однозначной закономерности. Можно полагать, что зависимость коэффициента Пуассона от температуры определяется не только минеральным составом, но и особенностями структуры горной породы. Так, например, в работе Иудина М. М. ( Иудин, 2012 ), которая посвящена модели расчета обобщенного коэффициента Пуассона мерзлых пород, отмечается, что на формирование коэффициента Пуассона в породном массиве оказывает влияние трещиноватость горных пород. В настоящей работе для оценки принято допущение о неизменности величины ν под влиянием теплового поля. С учетом принятых допущений, параметров физических свойств минералов и формулы (13) температурная зависимость модуля упругости может быть записана в удобном для расчета модуля упругости виде:

E ( T) = A n ■ V p ( T) 2 ,                                             (14)

где А п – коэффициент, равный 2,29 для гранодиорита и 2,24 для аляскитового гранита; V p ( T ) – скорость продольных волн при температуре Т , км/с.

Для определения температурной зависимости скорости продольных волн V_p ( T ) воспользуемся выражением следующего вида ( Результаты…, 1993 ):

V p ( T) = V p⁰ + A p V p ( T),                                      (15)

где V p⁰ - скорость при нормальных условиях; A _PV P (T) - изобарическая поправка скорости с учетом температуры.

Для расчета поправки A _PV_P ( T) в работе ( Результаты..., 1993 ) на основе анализа экспериментальных данных по основным группам осадочных и кристаллических пород Балтийского щита предложена аппроксимирующая зависимость следующего вида:

A _PV_P ( T) = 1 - exp[ a •( T - 20)],                                    (16)

где a ® 0,002-0,003 (значение температуры в °С).

Коэффициент линейного теплового расширения р , характеризующий способность породы изменять свои линейные размеры при изменении температуры, зависит от минерального состава. Как отмечалось ранее, для расчета среднего коэффициента линейного теплового расширения полиминерального агрегата Новиком Г. Я. и Зильбершмидтом М. Г. в работе ( Новик и др., 1994 ) рекомендована зависимость (3). Однако использование формулы (3) для расчетной оценки р при повышенной температуре может приводить к погрешности, которая обусловлена неучетом релаксационных явлений на границах между минералами. Так, например, в работе американских исследователей Richter D. и Simmons G. ( Richter et al., 1974 ), в которой рассматриваются результаты измерений теплового расширения магматических работ, показано, что значения коэффициента теплового расширения, рассчитанные по экспериментальным данным и по формуле (3), могут различаться более чем на 100 %.

В работе Зарайского Г. П. и Балашова В. Н. ( Зарайский и др., 1981 ) предложен метод расчета теплового расширения горных пород на основе минерального состава с учетом избыточного линейного расширения по следующей зависимости:

Δ l / l о = Δ l / l о ( мин ) + Δ l / l о ( изб ) .                                              (17)

Первый член в правой части выражения (17) определяется как третья часть арифметического средневзвешенного значения объемного теплового расширения породообразующих минералов. Для расчета избыточного линейного расширения породы Δ l / l о(изб) авторами работы ( Зарайский и др., 1981 ) предложен метод парных комбинаций осей эллипсоидов теплового расширения, основанный на суммировании вкладов в избыточное расширение породы от всех возможных парных комбинаций осей с учетом вероятности их встречи в соответствии с объемной долей минералов в породе:

A l / l_0(u== ¹ Y w , ■ w_k2YL_k2,                               (18)

О ( Изб )                   к 1      к 2        к 1, к 2

⁹ к 1, к 2

где k 1, k 2 – минералы, слагающие породу; j 1, j 2 – оси эллипсоида теплового расширения; w k 1 , w k 2 – объемная доля каждого из минералов; L k 1, к 2 = |a l k 1 / 1 _{0 к} 1 -A l k /ll _{0 к 2}| - абсолютное значение разности линейного расширения для каждой пары сравниваемых осей.

Следует отметить, что предложенный в работе (Зарайский и др., 1981) метод расчета теплового расширения горных пород основывается на обнаруженном экспериментально эффекте разуплотнения пород при нагревании, сопровождающимся существенным возрастанием пористости и проницаемости, что наиболее сильно выражено для слабопористых и малопроницаемых пород (Зарайский и др., 1978). Экспериментально установленная универсальность отмеченного явления позволила связать его с анизотропией теплового расширения не только разных минералов, но и для одного зерна по разным кристаллографическим направлениям.

Расчетное значение коэффициента линейного теплового расширения β в интервале температуры Δ Т определяется из выражения

β=^{∆ l} ⋅ ¹

l o  ∆ T

.

Результаты и обсуждение

Результаты расчетов теплофизических свойств пород по минеральному составу при нормальных термодинамических условиях представлены в табл. 4.

Таблица 4. Расчетные параметры теплофизических свойств гранитоидов

(при нормальных термодинамических условиях)

Table 4. Calculated parameters of thermophysical properties of granitoids

(under normal thermodynamic conditions)

Порода	ρ , кг/м3	λ , Вт/(м ⋅ К)	С , Дж/(кг ⋅ К)	а = λ /( С ⋅ ρ), м/с	β . ∙106, 1/К
Гранодиорит	2650	2,3	788	1,10 ⋅ 10–6	8,4
Аляскитовый гранит	2560	3,4	759	1,75 ⋅ 10–6	8,9

Оцененные значения теплопроводности отражают особенности минерального состава рассматриваемых гранитоидов – значительное влияние содержания кварца, который характеризуется повышенным значением теплопроводности. Как и следовало ожидать, оцененные значения удельной теплоемкости пород отличаются незначительно, что обусловлено малой вариацией величины С для породообразующих минералов. Незначительные различия наблюдаются и для коэффициента линейного теплового расширения, некоторое влияние на величину которого также оказывает содержание кварца.

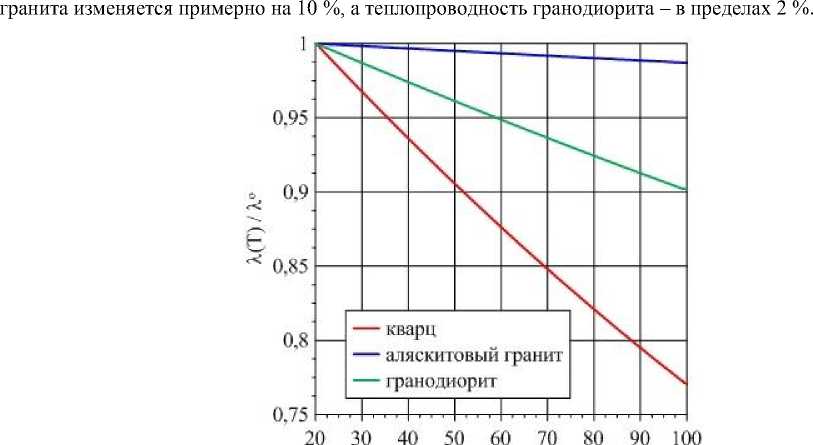
Рассчитанная по формулам (6) и (7) температурная зависимость теплопроводности кварца и рассматриваемых гранитоидов приведена на рис. 1 в нормализованном виде λ ( Т )/ λ ^о. Сильная зависимость теплопроводности кварца от температуры обусловливает различия в температурной зависимости теплопроводности горных пород, отличающихся содержанием данного породообразующего минерала (см. табл. 1). Так, например, при повышении температуры с 20 до 100 °С теплопроводность аляскитового

Температура. “С

Рис. 1. Температурная зависимость теплопроводности кварца и горных пород

Fig. 1. Temperature dependence of thermal conductivity of quartz and rocks

С учетом минерального состава пород (табл. 1) и свойств минералов (табл. 3) на основе формул (2, 9–11) выполнены оценки температурной зависимости удельной теплоемкости минералов и рассматриваемых скальных пород. При этом в отсутствие данных о температурной зависимости удельной теплоемкости биотита и роговой обманки, для этих минералов принимались значения, соответствующие нормальным условиям. Результаты выполненной оценки приведены на рис. 2.

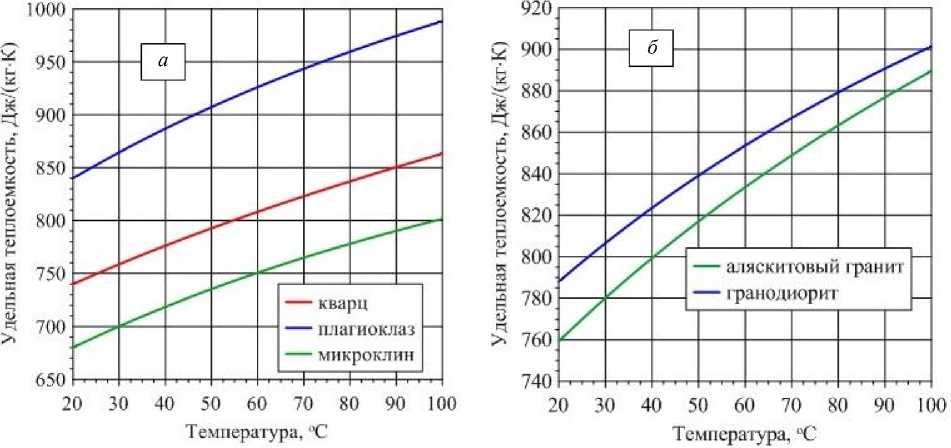
Рис. 2. Температурная зависимость удельной теплоемкости основных породообразующих минералов ( а ) и горных пород ( б ) Fig. 2. Temperature dependence of the specific heat capacity of the main rock-forming minerals ( a ) and rocks ( б )

Изменение удельной теплоемкости плагиоклаза (олигоклаза), который среди основных породообразующих минералов характеризуется относительно более высоким значением теплоемкости, в существенной мере определяет температурную зависимость удельной теплоемкости рассматриваемых горных пород. В большей степени такое влияние характерно для гранодиорита, в котором содержание плагиоклаза почти в 2 раза больше по сравнению с аляскитовым гранитом. При этом изменения удельной теплоемкости рассматриваемых горных пород практически не отличаются. Так, например, при повышении температуры до 100 °С удельная теплоемкость гранодиорита и аляскитового гранита повышается на 14 и 17 % соответственно.

Результаты расчетов температурной зависимости модуля упругости по формуле (14) с учетом зависимостей (15) и (16) приведены на рис. 3 в виде величины Е ( Т ), нормированной на значение модуля упругости при нормальных условиях Е ^о (средние значения Е в табл. 2).

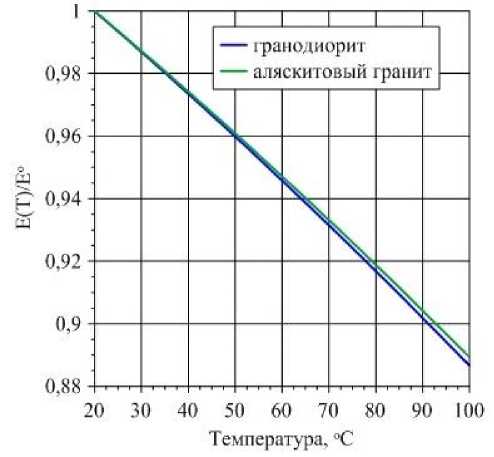
Рис. 3. Температурная зависимость модуля упругости горных пород

Fig. 3. Temperature dependence of the elastic modulus of rocks

Результаты оценки показали незначительные различия в температурной зависимости модуля упругости рассматриваемых гранитоидов. В интервале температуры 20–50 °С расчетные значения Е снижаются примерно на 4 %, при повышении температуры до 100 °С изменения модуля упругости не превышают 12 %.

Температурная зависимость теплового расширения гранитоидов (в % к состоянию при 20 °С), которая получена на основе выражений (17) и (18) и справочных данных о тепловом расширении породообразующих минералов ( Скиннер, 1969 ), приведена на рис. 4.

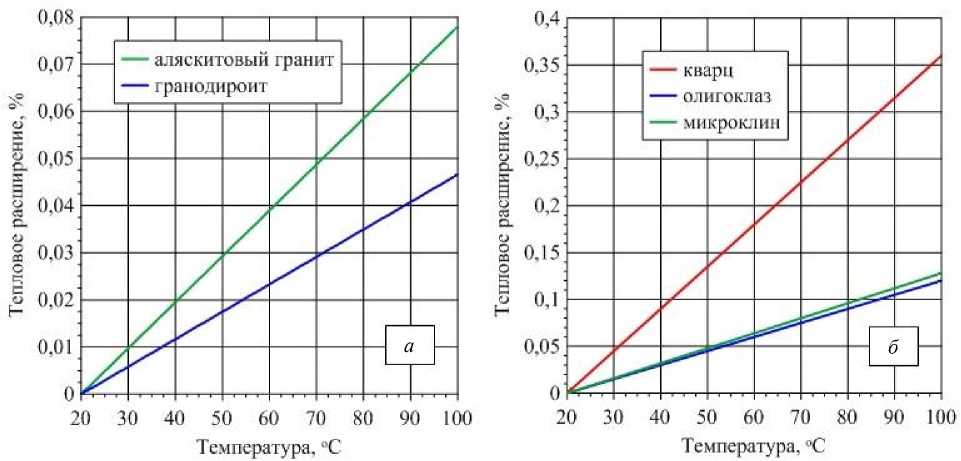
Рис. 4. Температурная зависимость теплового расширения горных пород ( а ) и объемного теплового расширения породообразующих минералов ( б ) Fig. 4. Temperature dependence of thermal expansion of rocks ( a ) and volumetric thermal expansion of rock-forming minerals ( б )

Рис. 4 наглядно иллюстрирует, что различия в тепловом расширении гранитоидов обусловлены содержанием основных породообразующих минералов, среди которых наибольшее тепловое расширение характерно для кварца.

Таким образом, на основе данных по минеральному составу выполнены расчетные оценки температурных зависимостей параметров физических свойств гранитоидов, которые в обобщенном виде приведены в табл. 5. В этой таблице представлены результаты оценки температуропроводности, которая характеризует скорость распространения тепла в породе, и комплекса β⋅ Е , определяющего, при прочих равных условиях, величину термических напряжений в породе.

Таблица 5. Относительное изменение свойств пород при нагревании от 20 °С до температуры Т Table 5. Relative change in rock properties when heated from 20 °C to temperature T

Свойство	Гранодиорит			Аляскитовый гранит
	Температура Т , °С
	30	50	100	30	50	100
Температуропроводность а = λ /( С ⋅ ρ)	0,975	0,934	0,863	0,961	0,900	0,772
Комплекс β⋅ Е	0,987	0,960	0,887	0,987	0,961	0,890

Кратко комментируя данные, приведенные в табл. 5, можно отметить, что при повышении температуры породы до 30 °С изменения рассматриваемых физико-технических свойств гранитоидов различаются незначительно. При более высокой температуре возрастают различия в изменении температуропроводности, что обусловлено содержанием в породах кварца, который характеризуется наиболее значительными изменениями теплопроводности при повышении температуры.

Заключение

На основе данных о минеральном составе гранитоидов Кольского полуострова (гранодиорит, аляскитовый гранит) выполнена теоретическая оценка теплофизических свойств пород при нормальных термодинамических условиях и представлены результаты прогнозной оценки параметров свойств пород в условиях повышенных температур в интервале от 20 до 100 °С.

При повышении температуры до 100 °С практически не наблюдается различий в относительном изменении (росте на 14–17 %) значений удельной теплоемкости пород по сравнению с нормальными термодинамическими условиями. Относительное изменение (снижение) коэффициента теплопроводности в наибольшей степени обусловлено содержанием кварцевой компоненты в минеральном составе пород, что вызвано ее доминирующим вкладом в температурную зависимость теплопроводности породы. По совокупности влияния на теплопроводность и удельную теплоемкость содержание этой компоненты определяет и характер изменения температуропроводности.

Применительно к задаче прогноза термомеханических явлений во вмещающем породном массиве практическое значение имеет температурная зависимость такого комплекса свойств, как β ⋅ Е , пропорционально которому формируются термические напряжения. Результаты выполненной оценки также демонстрируют отсутствие практических различий в температурной зависимости (снижении на 11 %) значений комплекса свойств для рассмотренных видов гранитоидов.

Работа выполнена в рамках темы НИР № 0226-2019-0026 "Развитие методологии создания подземных комплексов для атомных станций малой мощности в Арктике".

Автор выражает признательность кандидату технических наук Г. А. Ковалевой, предоставившей экспериментальные данные по минеральному составу и физическим свойствам горных пород.