Оценка влияния высокопористых абразивных кругов Norton из черного карбида кремния на точность формы шлифуемых деталей из ВТ20

размещения стружки. Сказанное снижает их засаливание и улучшает условия подачи СОЖ в зону резания, предотвращая появление прижогов и трещин [5–7].

Цель работы: оценить режущие свойства ВПК фирмы Norton из черного карбида кремния при шлифовании плоских деталей ВТ20 с учетом статистических методов, которые позволили дать их комплексную оценку по мерам положения и рассеяния [8].

Методика исследования. Опыты вели при следующих условиях: плоскошлифовальный станок модели 3Г71М; форма и размеры ВПК – 01 250×20×76 по каталогу фирмы Norton; объект исследования – образцы с размерами L×В×H = 40×40×40 мм, шлифуемые по площади L×В без выхаживания; технологические параметры – скорость резания vк = 35 м/c, продольная подача s пр = 6 м/мин, поперечная подача sп = 4 мм/дв. ход, глубина резания t=0,010 мм, операционный припуск z=0,10 мм; СОЖ – 5%-ная эмульсия Ак-вол–6 (ТУ 0258-024-00148845-98), подаваемая поливом на деталь с расходом 7–10 л/мин. Количество параллельных наблюдений n = 30. Выходные переменные процесса представлены в общем виде как yj, где индекс i = 1;4 - код ВПК Norton из черного карбида кремния: 1 – 37C46 I12 VP (базовый), 2 – 37C46 K12 VP, 3 – 37C60 K12 VP и 4- 37C80 K12 VP. ВПК г = 1 и 2 различаются твердостью: I (мягкие) и K (среднемягкие), а ВПК i = 2;4 - зернистостью: 46, 60, 80 [8]. Второй индекс j = 1;3 отражает принятый показатель отклонений от плоскостности [9]: основной EFEi1 = E F E imax характеризующий наибольшие отклонения реальной поверхности от прилегающей плоскости в пределах нормируемого участка; вспомогательные – EFEi2 = EFEia и EFEi3= EFEiq, ко- торые именуются соответственно средним арифметическим и квадратичным отклонениями от плоскостности. Количество параллельных опытов v = 1;30 .

Измерение отклонений от прямолинейности А _{( ф} р проведено на микрокаторе 2 - ИПМ (ТУ 2-234-229-89) в полярной системе координат, центром которой служит пересечение диагоналей квадрата 40 × 40 мм в 12-ти сечениях ф е [0^о ;330 о ] через 30^о по контуру детали, где индекс «1» в закодированном виде представляет расстояние точки измерения от начала полярной системы координат [10, 11]. Реальное расположение поверхности детали в точках ( ф ,1) может оказаться выше ( + А _{( ф} 1) ) или ниже ( -А _{( ф} 1) ) начала координат, которые именуются соответственно вогнутостью и выпуклостью [9]. В рамках данного ис следования режущих способностей ВПК i = 1;4 макроотклонения должны быть представлены вещественной переменной, характеризующей расстояния между выпуклыми и вогнутыми участками поверхности. Далее отклонения от прямолинейности преобразованы в отклонения от плоскостности EFE . , исходя из следующих соображений: - при одноименном расположении всех точек поверхности на наружном контуре конкретной v -той детали относительно начала координат

EFE ^ ,1> =А ( , ^ ,          (1)

• -    при разноименных частных видах отклонений от прямолинейности относительно начала координат

EFE_W )v = ( А но +А ^ ,₀ )„ ,      (2)

где А ноiv - начало отсчета для конкретной детали для операционной партии v = 1;30, взятое по модулю наибольшего альтернативного отклонения от прямолинейности, выявленного среди точек измерения     (ф, р),ф = [00;3 3 00], р - 0;0,5;1.

По (1), (2) находим EFE ( _ф 1) _iv для каждого опыта при переменной i = 1; 4. Далее они подлежат трансформированию с учетом выбранного показателя отклонений от плоскостности:

EFE max = EFE „ = ( S [ EFE v „„ ]} / 30 ,       (3)

v

EFE a = EFE , 2 = ( S ^[ S EFE „.]}/30,       (4)

v 12 ф

EFE q = EFE , 3 = { S A;[ S ( EFE , „)T'}/30. (5) v 12 ф

Учитывая неустойчивость и стохастическую природу процесса шлифования, интерпретацию наблюдений ведем с привлечением статистических подходов, рассматриваемая их случайными величинами (СВ). В условиях эксперимента они представлены множествами

{ y . }, i = 1;4, j = 13, v = 1^30.            (6)

В работах [10–12] приведена методика интерпретации экспериментальных данных с использованием статистических методов, которые разделяются на две группы: параметрическую и непараметрическую (в частности, ранговую). Каждый метод статистики имеет свою область рационального применения. Для применения параметрического метода необходимо, чтобы (6) удовлетворяли требованиями нормальности распределений и однородности дисперсий. Второе ограничение к (6) должно выполняться наиболее строго. Изложенные требования при шлифовании чаще всего нарушаются в той или иной мере, что может сопровождаться значимым смещением оценок, доверительных границ и коэффициентов доверия. Это заставляет обращаться к непараметрической теории, свободной от перечисленных ограничений. С целью снижения трудоемкости вычислений, присущих статистическим методам, в работе использована программа Sta-tistica 6.1.478.0. Статистические методы позволяют предсказать следующую информацию по одномерному распределению частот (6) [10–13]: - по мерам положения (опорным значениям):

средним yj = y...,(7)

медианам у. ;(8)

• -    по мерам рассеяния (прецизионности):

стандартам отклонений SDij,(9)

размахам Ri. = (ymax - ymm ) y, квартильным широтам

КШ. = \y0,75 — y0,25 )j ;

• -    по мерам формы распределений, в частности асимметрии (скошенности):

Asj= [3( y - у )/SD ]..(12)

На частотах (7), (9), (10) базируется параметрический метод, а на (8), (11) – ранговые статистики. В условиях непараметрических статистик (3) – (5) трансформируются от средних на медианы, которые выявляются программой путем ранжирования последовательностей вида: {( EFE .) _max} _v , ^{{( EFE}i) a ^} V , ^{{( EFE} i ) q ^} v , v = 1;³⁰ . Влияние непараметрического метода на меры положения количественно оценено медиа нн ыми коэффициентами при одноименных i = 1; 4 :

K м_в = ( EFE I EFE . j          (13)

K m,„ = ( mEFEIEFE . ) , .         (14)

Оценку работоспособности кругов i = 2; 4 относительно базового ВПК 37C46 112 VP ( i = 1) ведем для обеих характеристик одномерного распределения частот (6):

Kj = (~iI~i)v,(15)

Kij = (ml) ImA)j,(16)

Кст ji = (SDJ SD^,(17)

Кст j2 = (RJ Rj(18)

Кст j3 = (КШ11 КШi)j.(19)

Коэффициенты (14), (16) – (19) необходимы для комплексной оценки режущих способностей абразивных кругов и расширения информационной базы при многокритериальном управлении процессом шлифования с использованием моделей многомерного дисперсионного анализа (МДА) с учетом конструктивных особенностей и служебного назначения деталей. Опытный медианный коэффициент (13) позволяет оценить скошенность кривых распределений.

Результаты исследования и их обсуждение. Результаты тестирования (6) на гомоскедастичность и нормальность распределе- ний (нуль-гипотезы H0 ) представлены в табл. 1, где для подтверждения однородности дисперсий проведено тестирование по трем группам критериев (to = 1; 3): 1 - Хартли, Кохрена, Бартлетта (в программе представлены одной совокупностью); 2 – Левене; 3 – Брауна-Форсайта. Условием принятия H0 по гомогенности дисперсий для каждого критерия является выполнение строгого неравенства: a jto < 0,05, а по всем тестированиям to = 1; 3 принятие f, в пользу H0 из условия: f, G [2;3]. Как видно из таб. 1, такая ситуация имеет место для параметра EFEiа , когда H 0 приняты по статистикам Левене и Брауна-Форсайта (f, = 2). Для подтверждения H0 о нормальности распределении (6) воспользовались критерием Шапиро-Уилка. Нуль-гипотеза по этому критерию принимается, если выполняется строгое неравенство: aj > 0,5, где aj -надежность принятия H 0 при переменных i = 1; 4, j = 1; 3 . Выявлено, что H0 отклонены полностью в 12-ти случаях тестирования (6) (таб. 1). Как видно из рис. 1, различные методы расчета показателей отклонений от плоскостности, оперируя одними и теми же (6), оказывают существенное влияние на гистограммы качества.

Таблица. 1. Тестирование (6) на гомоскедастичность и нормальность распределений

Проверка на гомоскедастичность				Проверка на нормальность распределений
Параметр	по статистикам ω			Круг	по параметрам
	1	2	3		EFE i1	EFE i2	EFE i3
				1	0,0004	0,4538	0,1725
EFE i 1 = EFE imax	0,196	0,117	0,370	2	0,0074	0,0648	0,1327
EFE i 2 = EFE ia	0,134	0,026	0,047	3	0,0307	0,0446	0,2040
EFE i 3 = EFE iq	0,171	0,068	0,157	4	0,0048	0,1921	0,0207

Примечание: критерии ω : 1 – Хартли, Кохрена, Бартлетта, 2 – Левене, 3 – Брауна-Форсайта; круги i – см. методику эксперимента

Сказанное в табл. 1 отражено различными надежностями отклонений от нормальности распределений. Как видно из рис. 1б, наибольшая величина a12 = 0,4538 имеет место для показателя EFE1 а. Отмеченные нарушения, накладываемые на СВ со стороны параметрического метода, вызвали необходимость воспользоваться ранговыми статистиками. Приводимые параллельно результаты прогнозирования для гауссо-вого конкурента носят информационный характер и служат для подтверждения его недостаточной адекватности «на чужом поле». Опорные величины и предсказанные на их основе (13), (15), (16) представлены в табл. 2. Дополнительно информацию по (8), (10), (11) иллюстрируют описательные статистики на рис. 2 по всем показателям отклонений от плоскостности, которые наглядно характеризуют расположение одномерных распределений частот между собой. Полученные результаты следует принимать во внимание и использовать для повышения эффективности шлифования.

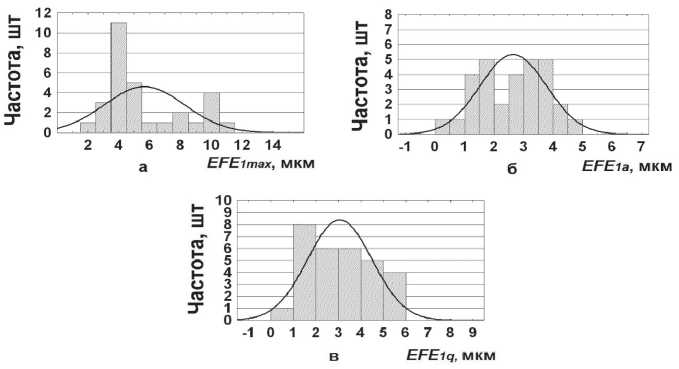
Рис. 1. Гистограммы качества с наложением кривых нормального распределения при шлифовании ВПК 37С46 I12 VP по показателям EFE ₁₁ (а), EFE ₁₂ (б), EFE ₁₃ (в)

Таблица 2. Влияние кругов на меры положения отклонений от плоскостности

Параметр j = 1;3	Круг	у ( TFE), мкм	~ ( TFE), мкм	У (TFE), мкм	my ( TFE), мкм	K m j (13)	K j (15)	A K j (16)
EFE i 1 = EFE imax	1	5,633 (5)	4,500 (5)	6,108 (6)	5,125 (5)	0,799	1,000	1,000
	2	6,033 (6)	5,000 (5)	6,108 (6)	5,125 (5)	0,829	1,111	1,000
	3	6,267 (6)	6,000 (5)	6,108 (6)	5,125 (5)	0,957	1,333	1,000
	4	6,500 (6)	5,000 (5)	6,108 (6)	5,125 (5)	0,769	1,111	1,000
EFE i 2 = EFE ia	1	2,629 (4)	2,750 (4)	2,896 (4)	2,877 (4)	1,046	1,000	1,000
	2	2,840 (4)	2,500 (4)	2,896 (4)	2,877 (4)	0,880	0,909	1,000
	3	3,345 (4)	3,667 (4)	2,896 (4)	2,877 (4)	1,096	1,333	1,000
	4	2,770 (4)	2,589 (4)	2,896 (4)	2,877 (4)	0,935	0,941	1,000
EFE i 3 = EFE iq	1	3,041 (4)	2,932 (4)	3,446 (4)	3,174 (4)	0,964	1,000	1,000
	2	3,317 (4)	2,713 (4)	3,446 (4)	3,174 (4)	0,818	0,925	1,000
	3	3,895 (4)	4,045 (5)	3,446 (4)	3,174 (4)	1,038	1,379	1,000
	4	3,531 (4)	3,007 (4)	3,446 (4)	3,174 (4)	0,851	1,025	1,000

Примечание: ВПК i – см. методику эксперимента, в скобках указаны TFE [7].

По (12), (13) легко выявить случаи асимметрии распределений (6). При KMij <1 эксцесс является положительным, который способствует повышению эксплуатационных показателей машин. По результатам эксперимента опытные медианы ~yij в девяти случаях из двенадцати оказались меньше средних yij . Эти случаи шлифования отмечены (13), равными KMj = 0,77 - 0,94. Только при KM41 = 0,77 сдвиг медианы относительно средней привел к повышению точности от TFE 6 до TFE 5 (для EFE4max ). В альтернативном случае при KMij <1 также на один квалитет точности EFE33 превысил аналог по среднему EFE3,, а по остальным параметрам сдвиг уу относительно у у, протекал внутри TFE. Проведение второго этапа одномерного дисперсионного анализа на предмет множественного сравнения опорных величин на 5%-ом уровне значимости выявило две новые закономерности.

Во-первых, все ожидаемые медианы для основного показателя mEFE i 1 , i' = 1; 4 предсказаны на один квалитет точности формы ( TFE 5) выше, чем по средним ( TFE 6). По вспомогательным показателям EFE_y , j = 2;3 снижение отклонений от плоскостности оказалось менее интенсивным и протекало внутри одного TFE (таб. 2). Во-вторых, коэффициенты (16), предсказанные по ожидаемым медианам, оказались равны единице. С позиций технологии шлифования следует принять, что при шлифовании деталей ВТ20 варьирование твердости ВПК i = 1;2 от I

(мягкой) до К (среднемягкой) и зернистости от 46 до 80 (ВПК i = 2; 4) не оказало значимого влияния на точность формы. Таким образом, выявлена высокая робастность точности формы деталей ВТ20 по медианам к переменным условиям шлифования. Для подтверждения сказанного отметим, что в идентичных условиях шлифования быстрорежущих пластин ВПК из синтеркорунда 5SG варьирование твердости привело к росту отклонений от плоскостности по всем показателям EFEj, j = 1;3 на один квалитет, а варьирование зернистости – сопровождалось, напротив, снижением их величин на один квалитет [14].

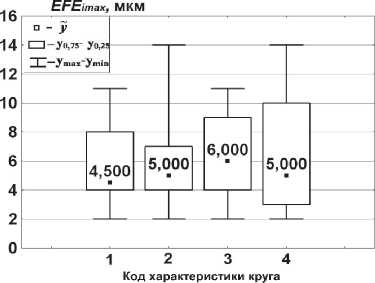
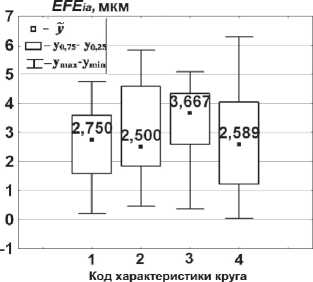
а                                              б

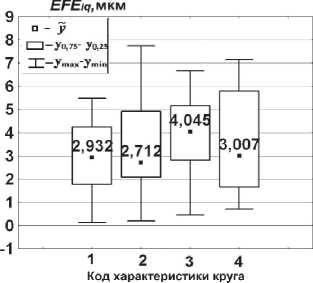
В

Рис. 2. Описательные непараметрические статистики при шлифовании ВПК i = 1;4 по показателям отклонений от плоскостности: а – EFE i 1 , б – EFE i 2 , в – EFE i 3

По прогнозируемым медианам основной показатель mEFE,max превышает вспомогательные: mEFˆE - в 1,78 раза, mEFˆE - в 1,6 раза, аq соотношение между последними - mEF’E,q / mEFE,а = 1,1. Уточним практическое использование показателей отклонений от плоскостности. Основной показатель EFEmax характеризует наиболее неблагоприятные условия работы ВПК. В рамках проведенного исследования он имеет неоспоримый приоритет. Однако оказалось, что все mEF'E,max характеризуются общей средней медианой, т.е. все ВПК i = 1;4 по наибольшему отклонению от плоскостности предсказаны равноценными. Возможно на точность деталей большую роль оказало состояние станка, а не режущие способности ВПК. Вторым не менее важным направлением использования полученных результатов служит поиск поправочных коэффициентов (14) для базовых моделей МДА, учитывающие условия шлифования конкретных деталей. Известно, что модели МДА априори предсказывают информацию по EFEmax , а модели точности формируются случайными величинами [15]. В этом случае при поиске (14) следует привлекать показатель EFEq . В крайнем случае можно воспользоваться показателем EFEа , имея в виду то, что он даст прогнозируемую погрешность в пределах 10%. В данном случае шлифования деталей из сплава ВТ20 коэффициенты (16) также оказались равными единице. В силу сказанного оценку режущих способностей ВПК i = 1;4 следует вести с учетом прецизионности процесса, что позволяет реализовать привлечение статистических методов.

Меры рассеяния оказались более вариабельными к переменным условиям шлифования по сравнению с (13) и (14). В таб. 3 представлены все три параметра прецизионности (9) – (11). В условиях приоритетного использования непараметрического метода предпочтение отдаем результатам, предсказанным по квартильным широтам (11) и коэффициенту стабильности (19). Из таб. 3 и рис. 2,а видно, что по показателю EFEimax наименьший КШ21 = 3 мкм предсказан для ВПК i = 2, т.е. при зернистости 46 и твердости К (среднемягкой), прецизионность работы которого оценивается коэффициентом стабильности (19), равным Кct213 = 1,333. Как видно из рис. 2,а, указанная стабильность формирования EFEmax обеспечена снижением процентиля у о 75<23). При этом для ВПК i = 1; 3 нижние процентили y0 25(i3), i = 1; 3 сохраняются на одном уровне – 4 мкм. По вспомогательным показателям EFEjj, j = 2;3 наименьшая КШ (таб. 3) предсказана при шлифовании ВПК 37С60 К12 VP ( i = 3): КШ32 = 1,75 мкм, КШ33 = 2,346 мкм. Однако для окончательного принятия решения по стабильности работы ВПК целесообразно воспользоваться описательными статистиками

(рис. 2 б, в), иллюстрирующими расположение КШ относительно размаха и медианы. Как видно из рис. 2,б, при шлифовании деталей ВТ20 кругом 37С46 I12 VP ( i =1) для показателя EFE 12 мера рассеяния относительно ВПК i = 3 возросла от 1,75 до 2 мкм. Однако его процентиль ( У _{0 75}, У 025 ) 12 относительно аналога для ВПК i = 3 сместился ниже. Аналогическая ситуация имеет место и для КШ по показателю EFE_{i 3} . В обоих случаях j = 2;3 возросло количество деталей с меньшими отклонениями от плоскостности, вплоть до TFE = 2,5 мкм по повышенной относительной геометрической точности [7]. С изложенных позиций даже ВПК 37С80 К12 VP ( i = 4 ) немного уступает кругу i = 3 по рассеянию точности деталей для показателя EFE ₄ q , а по EFE ₄ а даже его использование при шлифовании имеет преимущества перед ВПК i = 3 .

Таблица 3. Оценка режущих способностей кругов по мерам рассеяния и коэффициентам стабильности (17) – (19)

Параметр j = Й3	Круг	SD ij , мкм	R ij , мкм	КШ ij , мкм	К ст ijr
					r =1 (17)	r =2 (18)	r =3 (19)
EFE i 1 = EFE imax	1	2,593	9,000	4,000	1,000	1,000	1,000
	2	3,306	12,000	3,000	0,784	0,750	1,333
	3	2,840	9,000	5,000	0,913	1,000	0,800
	4	3,767	12,000	7,000	0,688	0,750	0,571
EFE i 2 = EFE ia	1	1,122	4,547	2,000	1,000	1,000	1,000
	2	1,573	5,380	2,750	0,713	0,845	0,727
	3	1,268	4,714	1,750	0,885	0,965	1,143
	4	1,658	6,250	2,833	0,677	0,728	0,706
EFE i 3 = EFE iq	1	1,429	5,359	2,468	1,000	1,000	1,000
	2	2,061	7,565	2,847	0,693	0,708	0,867
	3	1,660	6,208	2,346	0,861	0,863	1,052
	4	2,029	6,434	4,132	0,704	0,833	0,597

Примечание: круги i – см. методику эксперимента

По параметрическим мерам рассеяния (4), (5), которые носят рекомендовательный характер, наибольшая стабильность процесса предсказана при шлифовании титановых деталей ВПК i =1;3. Сказанное в статье представлено только по раз-махам (рис. 2а-2в). Если по результатам исследования решается одна из возможных задач, то следует воспользоваться следующими рекомендациями:

• -    для поиска моделей МДА в качестве базового ВПК следует принять характеристику 37С 46К12 VP;

• -    при оценке относительной прецизионности процесса в качестве базового инструмента целе-

• сообразно принять ВПК 37С60 K12 VP.

Выводы:

• 1.    С позиций опорных значений все медианы наблюдений EFE_y , i = 1;4 , j = 1;3 на 5%-ом уровне значимости признаны извлеченными из одной генеральной совокупности и оцениваются общей величиной EFE , j , j = 1; 3 .

• 2.    Определяющим фактором в выборе кругов оказалась прецизионность формирования отклонений от плоскостности. При поиске МДА шли-

• фование деталей из сплава ВТ20 следует вести ВПК 37C46 K12 VP, а при оценке относительной стабильности процесса - ВПК 37C60 K12 VP.

• 3.    В условиях нарушений гомоскедастичности и нормальности распределений наблюдений оказалась целесообразной их статистическая интерпретация с привлечением непараметрического метода и программного продукта Statistica 6.1.478.0, которая при равенстве мер положения позволила оценить режущие способности ВПК с учетом прецизионности процесса шлифования.

  
  
  
  

• 8.

• 9.