Оценка возмущений в минимаксном фильтре

Одна из важнейших задач при разработке сис-

2. При w_k = 1,5 , к = 1,

...

, N наблюдается

тем автоматического управления – построение эффективных алгоритмов оценивания состояния системы [1]. Повысить эффективность этих алгоритмов можно за счет оценки возмущений, дейст-

схожая с первым случаем картина (рис. 6). При постоянных максимальных возмущениях, начиная со 2 шага, информационные множества стягиваются в точку.

вующих на систему, и построения адаптивного алгоритма [2]. Пусть процессы в системе управления описываются следующим образом:

x k + 1 = Ax k + ^rw k , У к + 1 = Gx k + 1 ^{, x} k ^e R n , (1) w k e W c R m ,k = 0 , 1 ,...,N -1.

Матрицы A , Г и G заданы следующим образом:

0,9976 0,04639 A =,

I -0,09278 0,8584

Г =

' 0,1189 - 10 ^-5

_v 4,639 - 10 ^-2 .

, G = ( 1 0 )

Множества X ₀ , W заданы следующим образом: X ₀ = { x e R ² |-7,5 - 10 ^-4 <  x (1) <  7,5 - 10 ^-4 , -0,03 <  x (2) <  0,03},                        (3)

W ={ w e R |-1,5 <  w <  1,5} .                 (4)

1. Особенности изменения вектора состояния

Рассмотрим разные варианты реализации возмущений.

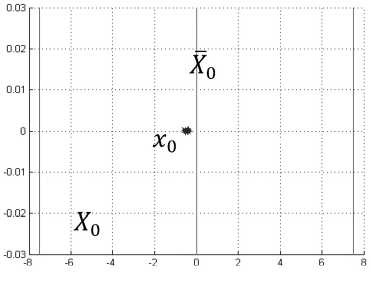
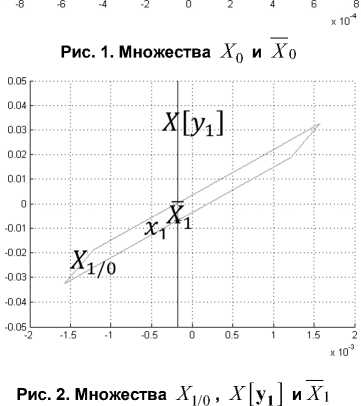
1. Пусть w_k =- 1,5, k = 1,..., N . На рис. 1-5 изображены множества прогнозов X_{k + 1/ k} , множества, совместимые с измерениями X [ у_к ] , информационные множества X к + 1 и истинные значения х_к .

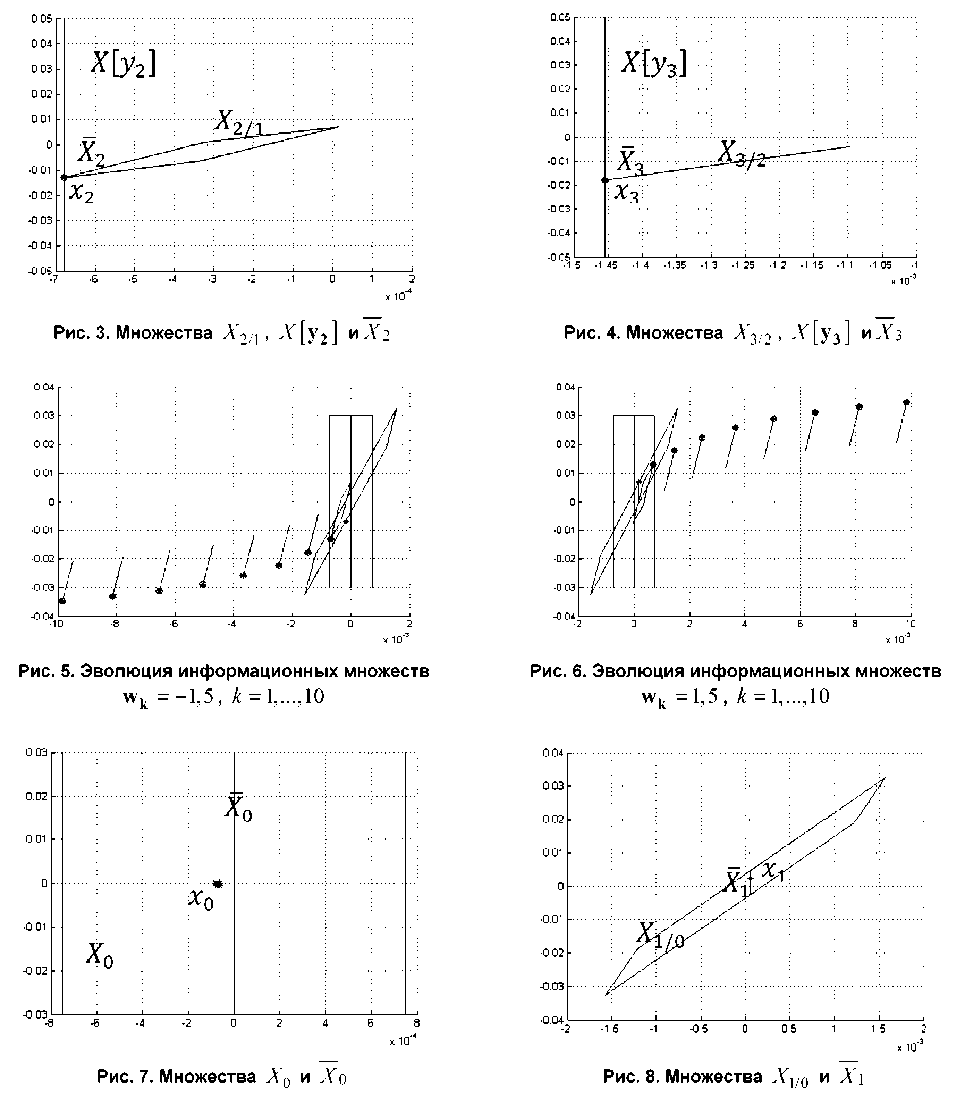
• 3.    Рассмотрим случай, когда возмущения постоянны, но не максимальны: w k = 0,5, к = 1,..., N (рис. 7-11).

• 4.    Рассмотри вариант, когда возмущение выходит за допустимое множество. Пусть множество W остается неизменным, но w k = 2,5, к = 1,..., N (рис. 12–14).

• 2.    Адаптивная итерационная процедура

При постоянных не максимальных возмущениях информационные множества до 10 шага не стягиваются в точку, но размер множеств постепенно уменьшается.

Уже на первом шаге истинное значение не попадает во множество прогнозов и информационное множество. На втором шаге истинное значение также не попадает во множество прогнозов и пересечение множества прогнозов с множеством, совместимым с измерениями, получается пустым.

Пусть нам известно, что возмущения являются постоянными, но истинное значение возмущения не известно. Как видно из (1) и (2) при постоянных

Оценка возмущений в минимаксном фильтре

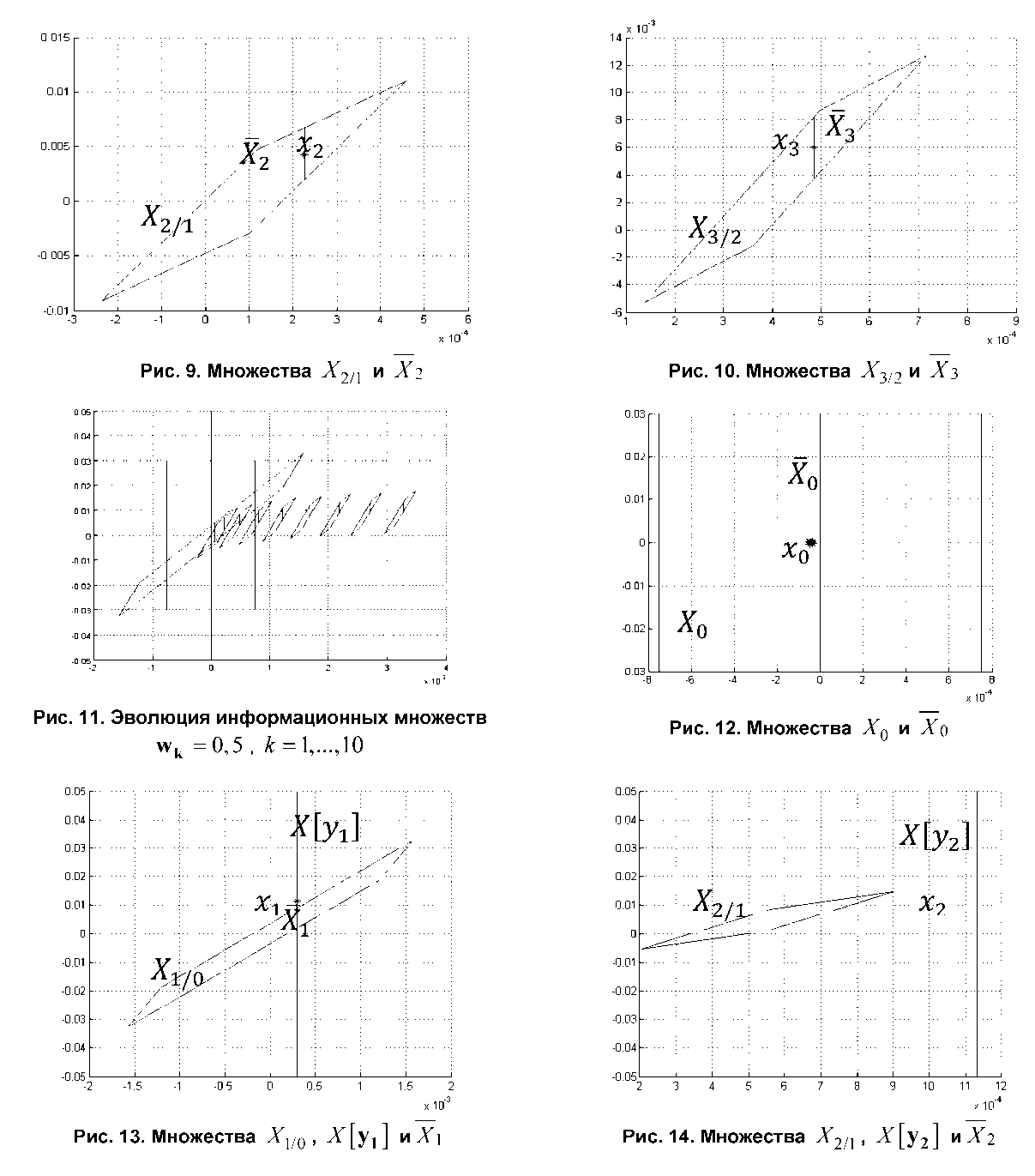
максимальных возмущениях, начиная со 2 шага, информационные множества стягиваются в точку. Также из (3) видно, что в случае, когда значение возмущения выходит за границы заданного множества, на 2 шаге пересечение множества прогнозов и множества, совместимого с измерениями , является пустым. Таким образом, при данных начальных условиях (2)-(4) за 2 шага можно определить какое возмущение реализовалось: из множества, с границы множества или не из множества.

Построим итерационную процедуру, которая каждые 2 шага уменьшает множество возмущений на dw (Wi+2 = Wi - dw), пока информационное множество не стянется в точку. Если на очередном n шаге пересечение множества прогнозов и множества, совместимого с измерениями, является пустым, то необходимо вернуться на 2 шага назад и пересчитать полученные множества, начиная с п-2 шага. Этот случай соответствует тому, когда истинное значение возмущения принадлежит разности множеств wn е Wn - Wn_2. При этом если точность оценки множества dw достаточная, то в дальнейшем принимаем множество Wi = Wn_2. Если же необходимо более точно оценить множество Wi, то, начиная с n-2 шага, продолжаем выполнять процедуру, при этом

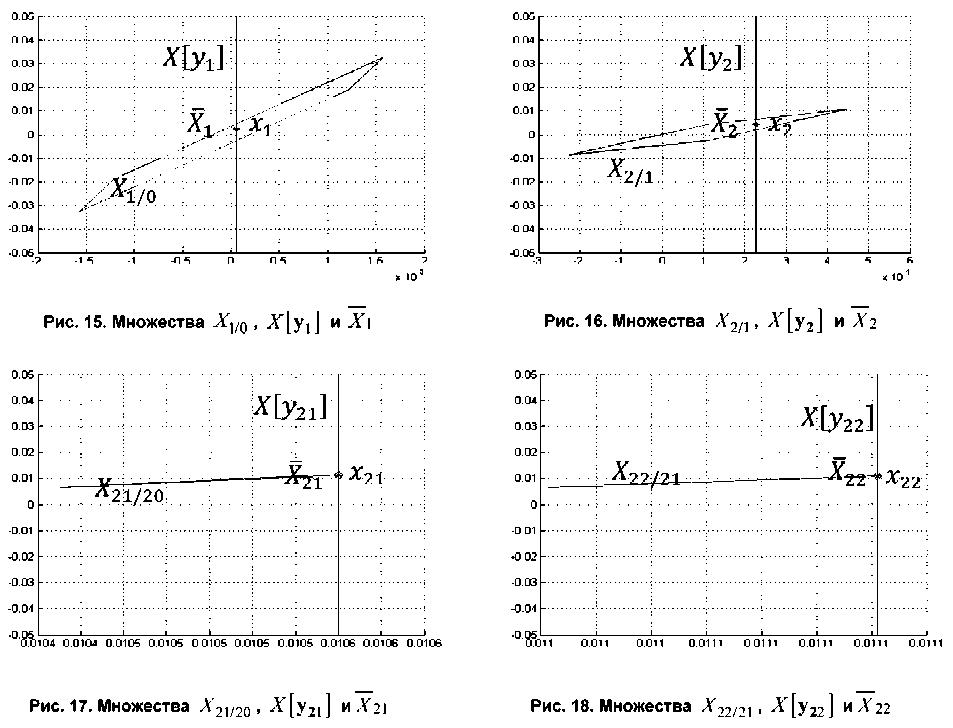
уменьшив dw . Рассмотрим случай, когда dw = 0,1 и w_i = 0,5 (рис. 15–18).

Заключение

Таким образом, с помощью данной процедуры за 21 шаг, постепенно уменьшая множество W , удалось сжать информационное множество в точку и тем самым повысить точность оценки состояния динамической системы. Можно обобщить данную процедуру для других реализаций, для этого требуется правильно подобрать значения k – число шагов, за которое можно распознать принадлежит ли возмущение границе множества, – а также определить, что возмущение реализуется извне множества и dw .