Оценка взаимовлияния региона и индустриального кластера: системно-пространственный подход

В последние тридцать лет в системе региональной экономической политики сформировался устойчивый тренд на использование кластеризации в качестве инструмента комплексного развития территорий. Одним из катализаторов этого процесса стало освещение в научной литературе опыта реализации наиболее успешных мировых кластерных инициатив (Силиконовая долина, Миннеаполис, технологический кластер Токио) [1].

Стремление регионов перенять этот опыт определило рост числа кластерных программ. Однако подобные инициативы часто имели нейтральное или даже негативное влияние на показатели социально-экономического развития территорий. Одной из ключевых причин таких результатов стала недостаточная изученность механизма интеракции двух территориально-экономических систем: региона и кластера [2]. Вследствие этого региональные органы власти не обладали необходимым теоретико-методическим инструментарием для количественной оценки существующего влияния и прогноза изменения динамики этого влияния под действием принимаемых ими управленческих решений. В итоге в системе кластерной политики допускались ошибки, способствовавшие появлению негативных эффектов воздействия кластера на социально-эко- номическое развитие региона и региона – на функционирование индустриального кластера.

В данной статье реализована одна из первых попыток комплексной оценки интеракции региона и кластера на примере деревообрабатывающего сектора. Гипотеза исследования основывается на идеях авторского системнопространственного подхода, согласно которому взаимовлияние индустриального кластера и региона восходит к эффекту кластерного мультипликатора-акселератора [3]. При этом влияние кластера на социальноэкономическое развитие региона иллюстрируют три кластерных мультипликатора (занятости, дохода, экспорта), воздействие региона на функционирование кластера – три соответствующих им кластерных акселератора.

Цель исследования – сформировать на основе результатов оценки взаимовлияния двух территориально-экономических систем концептуальный механизм интеракции региона и кластера, позволяющий моделировать последствия региональной кластерной политики для каждого из них. Предполагается, что такой механизм может быть положен в основу разработки и совершенствования региональных кластерных программ в сфере деревообработки, а в случае изменения вводных данных – применен для управления территориально-экономическими системами в рамках других видов экономической деятельности.

ОБЗОР ЛИТЕРАТУРЫ

В опрос взаимодействия региона с территориально-экономическими системами, размещенными в его границах, в академической литературе рассматривался с середины 1950-х гг. в контексте пяти пространственно-экономических школ (классической, социально-географической, институциональной, советской, математико-статистической) [3]. В начале 1990-х гг. в кластерной теории на основе этих школ сформировалось шесть подходов к изучению индустриального кластера. Основные отличия между ними отражены в табл. 1.

Таблица 1. Основные подходы к изучению индустриального кластера

Table 1. Key approaches to industrial clustering

Характеристика	Подход, примеры исследований
	Классический [4–8]	Сетевой [9–12]	Институциональный [13–16]
1. Интерпретация кластера	Географически локализованная группа взаимосвязанных взаимозависимых индустриальных единиц, взаимодействующих друг с другом, но сохраняющих отношения конкуренции	Территориально локализованная сеть автономных производственных единиц и связанных с ними сервисных компаний, объединенных общей цепочкой создания стоимости	Особая устойчивая форма пространственно-отраслевого партнерства, основанная на системе институциональных механизмов и соглашений
2. Связующая основа кластера	Локализованная географическая область	Цепочка создания стоимости	Система институциональных связей и соглашений
3. Территория и границы кластера	Географическая область, где размещены предприятия – члены кластера	Четких границ нет. На концептуальном уровне – географическая область, где локализована цепочка создания стоимости	Четких границ нет. На концептуальном уровне – зона действия институциональных связей и соглашений кластера
4. Генезис	Естественный, смешанный, искусственный	Естественный, смешанный	Естественный, смешанный
Характеристика	Системный [17–21]	Административный [22–25]	Агломерационный [26–30]
1. Интерпретация кластера	Локализованная пространственная система производственных организаций с особой средой и элементами координации экономической деятельности для достижения общих целей	Форма отраслей организации хозяйствования в границах одного или нескольких муниципалитетов	Форма индустриальной агломерации, локализованной в границах промышленного района, и создаваемая ею многофакторная среда
2. Связующая основа кластера	Многофакторное пространство	Территория одного или нескольких муниципалитетов	Территория как особое многофакторное пространство
3. Территория и границы кластера	Четких границ нет. На концептуальном уровне – пространство, где происходят интеракции между предприятиями кластера, формируется и действует территориально-экономическая система	Территория в границах одного или нескольких университетов в их административных границах	Промышленный район
4. Генезис	Естественный, смешанный	Искусственный, смешанный	Естественный, смешанный

Как следует из табл. 1, различия сводились к четырем параметрам: к интерпретации феномена индустриального кластера, к определению связующей основы территориальноэкономической системы, ко взглядам на природу территории и генезис кластера.

Под параметром «связующая основа кластера» в этом случае понимают интегративный элемент, объединяющий компоненты, входящие в состав индустриального кластера, в единую, целостную структуру.

Параметр «территория и границы кластера» воспроизводит пространство, которое авторы, работающие в рамках подхода, включают в состав географической области индустриального кластера на плоскости региона.

Параметр «генезис кластера» отражает взгляд на происхождение кластерных структур в контексте определенного теоретического подхода. Как показал анализ, в современной научной литературе выделяется три возможных генезиса индустриального кластера: естественный, искусственный и смешанный.

Естественный генезис рассматривает формирование индустриального кластера как результат свободной интеракции рыночных сил. Искусственный генезис описывает кластер как структуру, целенаправленно формируемую региональными или федеральными властями. Смешанный – выводит двухэтапный механизм, на первой стадии которого в регионе естественным путем складываются прото-кластерные структуры. На втором этапе при участии региональных или федеральных властей такие структуры превращаются в полноценные кластеры.

Независимо от системы теоретических подходов к интерпретации индустриального кластера в 1990–2010-х гг. в научной литературе сформировался комплекс методик, позволяющих исследовать влияние кластера на регион и влияние региона на кластер (табл. 2).

Представленные в табл. 2 методики активно используются в научных исследованиях для оценки воздействия индустриального кластера на регион и региона на индустриальный кластер. При этом в процессе подготовки научных работ исследователи согласуют положения выбранной ими методики с идеями теоретического подхода, в контексте которого они рассматривают индустриальный кластер. Такое согласование имеет два важных следствия.

Во-первых, в контексте системы работ выделяются подходы, которые используются чаще других (табл. 3).

Таблица 2. Компаративный анализ основных методик исследования влияния кластера на регион и влияния региона на кластер

Table 2. Comparative analysis of key industrial cluster and region mutual influence study methodologies

Характеристика	Методика, примеры исследований
	Статистическая [8; 31–33]	Регионалистическая [11; 34; 35]	Маркетинговая [36–38]	Ситуационная [39; 40]
Происхождение методики	Экономическая статистика	Урбанистка, региональная экономика	Маркетинговый анализ	Ситуационный подход в менеджменте
Объект анализа	Статистические зависимости между переменными, отражающими факторы региональной среды и параметры функционирования индустриального кластера	Взаимное изменение показателей, отражающих свойства региона и кластера	Мнения респондентов	Кейс (конкретная ситуация)
Результат процесса влияния	Формирование статистических зависимостей	Изменение параметров территориально-экономической системы	Социальноэкономические эффекты	Изменение ситуационных переменных
Основные методы	Регрессионный, факторный, корреляционный анализ	Матрицы «затраты – выпуск», оценка целевых показателей, сдвиговой анализ	Опрос, экспертная оценка, интервью	Кейс-стади

Таблица 3. Относительная частота использования методик исследования влияния кластера на регион и региона на кластер в контексте публикаций, основанных на существующих подходах, %

Table 3. Relative usage frequency of industrial cluster and region mutual influence study methodologies, %

Теоретический подход, лежащий в основе публикации	Методика
	Статистическая	Регионалистическая	Маркетинговая	Ситуационная
Классический	> 40	10–40	> 10	> 10
Агломерационный	> 40	0	> 10	0
Административный	> 40	10–40	> 10	0
Институциональный	> 40	> 10	> 10	> 10
Системный	> 40	10–40	> 10	> 10
Сетевой	> 40	10–40	0	0

В табл. 3 отражен процент работ, опубликованных с 1990 по 2022 г. в русле одного из шести теоретических подходов, в которых использована каждая из четырех методик или ее элементы. Ноль процентов в этом случае означает, что методика в контексте определенного теоретического подхода не использовалась. Исходя из этих данных, можно заключить, что наиболее востребованной и универсальной является статистическая методика. Относительно распространенной можно также считать регионалистическую, в то время как применение маркетинговой и ситуационной методик носит частный и во многом экспериментальный характер.

Во-вторых, как показал анализ, согласование теоретических подходов и методик в рамках научных работ достигается за счет системы показателей, которые вводятся в методику для проведения оценки.

С этой позиции сравнительно универсальными можно считать некоторые показатели социально-экономического развития региона, в том числе «ВРП / ВРП на число занятых / ВРП на душу населения»; показатели численности населения региона; показатели занятости / безработицы; индекс потребительских цен; число выпускников бакалавриата / магистратуры / аспирантуры; число лиц, проживающих в регионе и имеющих научную степень. В качестве универсальных может быть также рассмотрен ряд показателей функционирования кластера: коэффициенты локализации, специализации, урбанизации, концентрации, агломерации.

Другая группа показателей, напротив, вы-сокоспецифицирована. Например, классиче- ский, административный и агломерационный подходы глубоко прорабатывают географическое пространство индустриального кластера. В исследованиях, проводимых в рамках данных подходов, широко используются индикаторы развития транспортной инфраструктуры территории, а также весьма распространены относительные показатели, в структуре которых базой компарирования выступает площадь региона.

Особое место с этой точки зрения занимает административный подход. При ориентации на географическое измерение кластера он стремится увязать используемые индикаторы с официальными показателями региональной и (или) муниципальной статистики.

Системный, сетевой и институциональный подходы, в отличие от предыдущей группы, акцентируют внимание на социально-экономическом измерении кластера. В этих исследованиях используется более широкий набор индикаторов, характеризующих влияние рассматриваемой территориально-экономической системы на разные стороны жизни населения региона. Еще одна отличительная черта данного блока подходов – активное использование индикаторов внешнеэкономической деятельности территории.

Определенное исключение из представленных закономерностей составляет классический подход. По всем основным параметрам он относится к группе направлений экономической мысли, фокусирующейся на территориально-географическом измерении кластера, однако, подобно подходам, акцентирующим основное внимание на социальноэкономической стороне рассматриваемого конструкта, в его рамках глубоко прорабатываются показатели внешнеэкономической деятельности.

Из представленной аргументации следует, что в современной научной литературе для исследования влияния кластера на регион и воздействия региона на кластер используются концептуальные системы, состоящие из теоретического подхода (одного из шести) и методики исследования влияния (одной из четырех). По сути, такие системы акцентируют внимание либо на территориальногеографическом измерении индустриального кластера (концептуальные системы, основанные на классическом, административном или агломерационном подходе), либо на социально-экономическом (концептуальные системы, основанные на институциональном, сетевом и системном подходах).

Вместе с тем в современной научной литературе общепризнанным является положение о бинарной природе кластера, согласно которому структуры рассматриваемого типа одновременно сочетают в себе пространственно-географическое и социально-экономическое измерения.

Исходя из этого, можно заключить, что существующие концептуальные системы (теоретический подход плюс методика), используемые для анализа влияния кластера на регион и региона на кластер, не дают полной картины этого явления.

Для решения этой проблемы в 2018– 2020 гг. нами был предложен системно-пространственный (ранее называемый нами системно-агломерационным) подход, обеспечи- вающий равнозначный фокус сразу на двух измерениях индустриального кластера [41; 42].

С позиции этого подхода под индустриальным кластером следует понимать локализованную территориально-экономическую систему, одновременно обладающую свойствами социально-экономической системы и промышленной агломерации, в состав которой входят производственные и сервисные единицы с особой средой, образованной их интеракциями. В качестве связующей основы кластера рассматривается территория в границах индустриального района (индустриальной агломерации). Генезис кластера смешанный.

Исходя из свойств системы любое действие кластера на регион влечет ответный эффект. Соответственно, влияние индустриального кластера на регион целесообразно рассматривать совместно с влиянием региона на индустриальный кластер как единый процесс интеракции двух территориальноэкономических систем.

В предыдущих исследованиях нами была предложена и обоснована системно-пространственная модель этого процесса, в соответствии с которой влияние индустриального кластера, функционирующего в рамках любого вида экономической деятельности, на регион иллюстрируют три кластерных мультипликатора – занятости, дохода и экспорта, а воздействие региона на кластер – три соответствующих им кластерных акселератора (рис 1).

На основе этой модели предлагается реализовать оценку интеракции двух рассматриваемых в статье территориально-экономических систем.

Кластерный мультипликатор занятости

Кластерный мультипликатор доходов

Условные обозначения

Кластерный мультипликатор экспорта

Индустриальный кластер

Влияние индустриального кластера на социально-

Регион

экономическое развитие

региона

Кластерный акселератор занятости

Влияние региона на функционирование

Кластерный акселератор доходов

индустриального кластера

Кластерный акселератор экспорта

Рис. 1. Системно-пространственная модель взаимовлияния региона и кластера

Fig. 1. A system and spatial model of region and cluster mutual influence

МАТЕРИАЛЫ И МЕТОДЫ

Д ля проведения оценки взаимовлияния региона и индустриального кластера на первом этапе требуется формирование экспериментальной базы, предполагающее определение вида экономической деятельности (далее – ВЭД) и идентификацию кластеров, функционирующих в его рамках. В данном исследовании рассматривается ВЭД «Обработка древесины и производство изделий из дерева и пробки, кроме мебели». Выбор этого вида экономической деятельности связан с введенным с 01 января 2022 г. запретом на экспорт необработанной и грубо обработанной древесины ценных лиственных и хвойных пород. Данная мера стимулировала российские регионы искать пути развития обрабатывающих производств на своей территории. Одним из возможных решений, активно обсуждаемых как на региональном, так и на федеральном уровне, является кластерный подход.

Для идентификации существующих в России деревообрабатывающих кластеров предлагается использовать авторскую модификацию двухэтапного метода, предложенного изначально коллективом авторов во главе с Т.В. Миролюбовой [42]. Согласно этому методу, на первом этапе производится расчет коэффициента локализации ( LQ ), значение которого интерпретируется по шкале Э. Бергмана, Э. Фезера [43]. В соответствии с данной шкалой значения LQ > 1,25 рассматриваются как один из признаков наличия кластерной активности в определенном году.

Вместе с тем исследования 2010-х гг. показали, что значения индикаторов кластерной активности не статичны, а могут изменяться в сравнительно широком диапазоне в соответствии со стадией жизненного цикла кластера [44; 45]. Исходя из этого имеет смысл рассчитывать коэффициент локализации не за один год, а за хронологический период. Если в течение половины этого периода значение LQ > 1,25, то наличие первого признака кластерной активности предлагается считать установленным.

На втором этапе анализируется структура экспорта регионов, отобранных ранее по признаку коэффициентов локализации. Если в этих регионах в течение каждого года рассматриваемого периода наблюдается экспорт продукции, соответствующей профилю кластера, делается вывод о наличии в регионе индустриального кластера соответствующего профиля деятельности в рамках установленного хронологического периода.

Для проведения идентификации кластеров в данном исследовании выбран период с 2010 по 2019 г. Нижняя граница выделена исходя из критерия доступности статистических данных. Верхняя граница фиксирует последний год допандемийного периода. Согласно сложившемуся в научной литературе мнению, данные за последующие 2019– 2022 гг. находились под сильным влиянием эпидемического кризиса [46]. Соответственно, модель, разработанная на их основе, была бы несколько искажена.

Непосредственно оценка взаимовлияния региона и кластера в данном исследовании реализована на основе регрессионного анализа в программном пакете STATA. Для анализа воздействия индустриального кластера на регион в качестве индикаторов состояния региона (объясняемые переменные) выбраны наиболее широко используемые для этой цели показатели социально-экономического развития территории. В качестве индикаторов влияния (объясняющие переменные) использованы три кластерных мультипликатора – занятости, дохода и экспорта (табл. 4).

Анализ воздействия региона на кластер строится на использовании в качестве показателей состояния индустриального кластера (объясняемые переменные) основных индикаторов его функционирования, расчет которых возможен на основе данных российской национальной системы статистики. В качестве индикаторов влияния (объясняющие переменные) использованы три кластерных акселератора – занятости, дохода и экспорта (табл. 5).

С целью проведения более глубокого анализа и выделения закономерностей, реализация эффекта которых имеет годичный лаг, все переменные вводились в уравнение дважды: с индексом t и индексом t – 1, где t – год, за который реализуется анализ.

Таблица 4. Показатели оценки влияния индустриального кластера на социально-экономическое развитие региона

Table 4. Indicators of industrial cluster influence on social and economic development

Обозначение	Название	Значение	Источник (формула расчета)
Y 1	ВРП на душу населения, руб.	Уровни жизни и экономической активности населе ния региона	Единая межведомственная информационностатистическая система (далее – ЕМИСС)
Y 5	Начисление и поступление налогов, сборов и иных обязательных платежей в бюджетную систему РФ, тыс. руб.: поступило в консолидированные бюджеты субъектов РФ, всего, руб.	Доходы субъекта РФ	ЕМИСС
Y 6	Экспорт в фактически действовавших ценах, в дол.	Внешняя торговля (экспорт) региона	Рассчитано на основе данных статистического сборника «Регионы России» (далее — сборник «Регионы России») как сумма показателей «экспорт со странами дальнего зарубежья» и «экспорт со странами СНГ»
Y 7	ВРП, руб.	Экономическое развитие региона	ЕМИСС
Y 8	Перевозки грузов автомобильным транспортом, т	Объем перевозок грузов автомобильным транспортом	Сборник «Регионы России»
Х 1	Кластерный мультипликатор занятости (в году t ), ед.	Мультипликативные эффекты, связанные с уровнем занятости, порождаемые активностью кластера	„                                    A E Рассчитано по данным ЕМИСС по формуле X 1 =-- , A F где E – среднесписочная численность работников по полному кругу организации в регионе, всего; F – среднесписочная занятость работников по полному кругу организации в регионе в рамках конкретного ВЭД
Х 2	Кластерный мультипликатор доходов (в году t ), ед.	Мультипликативные эффекты, связанные с доходами населения, порождаемые активностью кластера	Рассчитано по данным ЕМИСС по формуле X 2 = ^~, A H где G – среднемесячная номинальная начисленная заработная плата на одного работника по полному кругу организаций, всего; H – cсреднемесячная номинальная начисленная заработная плата на одного работника по полному кругу организаций в рамках конкретного ВЭД
Х 3	Кластерный мультипликатор экспорта (в году t )	Мультипликативные эффекты, связанные с объемом экспорта из региона, порождаемые активностью кластера	Рассчитано по данным сборника «Регионы России» по формуле X 3 = ^-, где I - экспорт в фактически дейст-A J вовавших ценах, в дол.; J – экспорт в фактически действовавших ценах в рамках конкретного ВЭД, в дол.

Таблица 5. Показатели оценки влияния региона на функционирование индустриального кластера

Table 5. Indicators of region influence on an industrial cluster

Обозначение	Название	Значение	Источник (формула расчета)
Y 10	Коэффициент специализации кластера, ед.	В своей динамике показывает, как сильно рост специализации индустриального кластера влияет на приток рабочей силы в сектор, где функционирует эта территориально-экономическая система, в сравнении с показателями других регионов	Рассчитывается на основе данных ЕМИСС как коэффици- F ент локализации ( LQ ) по формуле Y 10 = ^   , где E - c Ec среднесписочная численность работников по полному кругу организации в регионе, всего; F – среднесписочная занятость работников по полному кругу организации в регионе в рамках конкретного ВЭД; Ec – среднесписочная численность работников по полному кругу организации в стране, всего; Fc – среднесписочная занятость работников по полному кругу организации в стране в рамках конкретного ВЭД

Окончание табл. 5

Обозначение	Название	Значение	Источник (формула расчета)
Y 11	Оборот деревообрабатывающих организаций, руб.	Отражает коммерческую деятельность организаций кластера	ЕМИСС
Y 12	Фокус кластера, ед.	Отражает уровень влияния кластера в регионе	Рассчитано на основе данных ЕМИСС по формуле F Y 12 = —, где E - среднесписочная численность работ ников по полному кругу организации в регионе, всего; F – среднесписочная занятость работников по полному кругу организации в регионе в рамках конкретного ВЭД
Y 15	Размер кластера	Относительный размер кластера	F Рассчитано по данным ЕМИСС по формуле Y 15 = —, Fc где F – среднесписочная занятость работников по полному кругу организации в регионе в рамках конкретного ВЭД; Fс – среднесписочная занятость работников по полному кругу организации в стране в рамках конкретного ВЭД
X 4	Кластерный акселератор занятости (в году t )	Акселеративный эффект изменения конъюнктуры регионального рынка труда на численность занятых в кластере	п                                    A F Рассчитано по данным ЕМИСС по формуле X 4 =-- , A E где E – среднесписочная численность работников по полному кругу организации в регионе, всего; F – среднесписочная занятость работников по полному кругу организации в регионе в рамках конкретного ВЭД
X 5	Кластерный акселератор доходов (в году t )	Акселеративный эффект от изменения уровня оплаты труда в регионе на уровень оплаты труда в кластере	.                                  A H Рассчитано по данным ЕМИСС по формуле X 5 =--- , A G где G – среднемесячная номинальная начисленная заработная плата на одного работника по полному кругу организаций, всего; H – среднемесячная номинальная начисленная заработная плата на одного работника по полному кругу организаций в рамках конкретного ВЭД
X 6	Кластерный акселератор экспорта (в году t )	Акселеративный эффект от изменения уровня экспорта с территории региона на уровень индустриального кластера	Рассчитано по данным сборника «Регионы России» по формуле X 6 = -^у, где I - экспорт в фактически действовавших ценах в дол.; J – экспорт в фактически действовавших ценах в рамках конкретного ВЭД, в дол.

Источник : составлено авторами (= compiled by the authors ).

Базовая модель анализа имеет вид

Yex = f ( M 1, M 2, M 3, N ) , (1) где Yex – объясняемая переменная, которая отражает один из показателей социальноэкономического развития региона в году t ; M 1 – кластерный мультипликатор занятости (в году t или t – 1); M 2 – кластерный мультипликатор доходов (в году t или t – 1); M 3 – кластерный мультипликатор экспорта кластера (в году t или t – 1); N – дополнительная переменная, которая фиксирует изменение одного из показателей социально-экономического развития региона (с индексом t или t – 1), отличного от Yex , который, в свою очередь действуя в системе с кластерными мультипликаторами, детерминирует зависимую переменную.

Первоначально регрессионное исследование предполагалось реализовать методом наименьших квадратов. Однако предварительный анализ выборочной совокупности и тестовое построение регрессий, с которыми были проведены тесты Персарана, Бройша – Погана (Вулдриджа), модифицированный тест Вальда, показали наличие в рассматриваемой системе данных ряда проблем, в том числе пространственной автокорреляции, временной автокорреляции и гетероскедастичности.

Наличие этих проблем вызвало необходимость обращения к процедуре Дрискала – Крея, которая относится к группе непараметрических методов и проводит работу со стандартными ошибками коэффициентов, снижая их чувствительность к общим формам поперечной и временной зависимостей.

Полученные в результате регрессионного анализа коэффициенты рассматриваются как количественное отражение общефедеральных закономерностей интеракции региона и индустриального кластера. Эти коэффициенты вводятся в структуру механизма интеракции региона и кластера (см. рис. 1) и картографируются. Сформированная таким образом концептуальная модель дает возможность спрогнозировать последствия вмешательства в систему интеракции региона и кластера, а также повысить эффективность взаимодействия двух территориально-экономических систем и нивелировать риск возникновения негативных эффектов от мер кластерной политики, реализуемой на территории субъекта РФ.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ

Р езультаты оценки влияния индустриального кластера на социально-экономическое развитие региона отражены в табл. 6.

Таблица 6. Результаты оценки влияния индустриального кластера на социально-экономическое развитие региона

Table 6. Assessment results of industrial cluster influence on social and economic development of a region

1. Воздействие индустриального кластера на ВРП региона, на душу населения
Показатель		Коэффициент	Driscoll–Kraay standard errors	t	P >  ItI	Нижние 95%	Верхние 95%
lY 1	X 1	0,0000490	0,0000117	4,18	0,003	0,0000220	0,0000761
	X 3	–0,0000283	0,0000171	–1,65	0,137	–0,0000677	0,0000112
	lY 6	0,0691823	0,0306592	2,26	0,054	0,0015179	0,1398825
Prob >  chi 2 = 0,0000; Within R-squared = 0,2562
2. Воздействие индустриального кластера на показатель «начисление и поступление налогов, сборов и иных обязательных платежей в бюджетную систему РФ, тыс. руб.: поступило в консолидированные бюджеты субъектов РФ, всего»
lY 5	С 1	0,0000189	8,08e-06	2,34	0,047	2,82е-07	0,0000375
	С 3	–0,0000348	0,0000181	–1,92	0,092	–0,0000766	7,07е-06
	lY 6	0,0852897	0,0462945	1,84	0,103	–0,0214657	0,0031
Prob >  chi 2 = 0,0031; Within R-squared = 0,51
3. Воздействие индустриального кластера на показатель «экспорт в фактически действовавших ценах, в дол.»
lY 6	С 1	0,0000988	0,0000432	2,29	0,051	–7,99e-07	0,0001984
	X 2	0,0077723	0,0019567	3,97	0,004	0,0032601	0,0122846
	C 3	0,0003301	0,0003470	9,52	0,103	0,0002502	0,0004101
	lA 8	0,3649533	0,2010392	1,82	0,107	–0,0986438	0,8285504
Prob >  chi 2 = 0,0000; Within R-squared = 0,3215*
4. Воздействие индустриального кластера на показатель «экспорт в фактически действовавших ценах, в дол.»
lY 7	X1	0,0000285	0,0000116	2,45	0,040	1,72e-06	0,0000553
	lС2	–0,0464597	0,0398167	–1,17	0,277	–0,1382770	0,0453577
	X3	–0,0000367	0,0000226	–1,62	0,143	–0,0000887	0,0000154
	lY8	0,1415049	0,0593306	2,39	0,044	0,0046881	0,2783216
Prob >  chi 2 = 0,0000; Within R-squared = 0,5858
5. Воздействие индустриального кластера на перевозки грузов автомобильным транспортом
lY 8	С 1	–0,0000488	0,0000113	–4,33	0,003	–0,0000747	–0,0000228
	С 3	0,0000110	0,0000286	0,38	0,711	–0,0000551	0,0000771
	lA 7	0,1905967	0,0999157	1,91	0,093	–0,0398093	0,4210027
Prob >  chi 2 = 0,0000; Within R-squared = 0,5815

Для интерпретации полученных коэффициентов, значение которых меньше 0,1, использована формула

( e^B - 1 ) - 100, (2)

где B – интерпретируемый коэффициент.

Как следует из табл. 6, влияние индустриального кластера на ВРП на душу населения описывает уравнение lY1 = 0,000049 x X1 - 0,0000283 x x X3 + 0,0691823 x lY 6.

Исходя из этого уравнения, рост значения кластерного мультипликатора занятости ( X 1) на единицу в году t определяет рост показателя ВРП на душу населения в году t на 0,00490012005196 %. Данная закономерность в целом соответствует мейнстриму современной экономической теории [47; 48].

Аналогично в рамки современной кластерной теории полностью укладывается вторая закономерность, отражаемая данным уравнением: рост показателя «экспорт в фактически действовавших ценах, в дол.» ( lY 6) в году на 1 % стимулирует рост ВРП на душу населения на 7,1631549774031 % [49; 50].

Воздействие индустриального кластера на индикатор «начисление и поступление налогов, сборов и иных обязательных платежей в бюджетную систему РФ, тыс. руб.: поступило в консолидированные бюджеты субъектов РФ, всего» характеризует уравнение lY5 = 0,0000189 x C1 - 0,0000348 x xC3 + 0,0852897 x lY 6, исходя из которого рост кластерного мультипликатора занятости в году t – 1 (С1) на единицу стимулирует рост поступления налогов, сборов и иных обязательных платежей в бюджет региона в году t на 0,00189001786062 %. Выявленный лаг воздействия (1 год) определяется продолжительностью налогового периода большинства налогов, уплачиваемых физическими лицами (прежде всего НДФЛ).

Рост кластерного мультипликатора экспорта в году t – 1 (С3) на единицу определяет снижение поступления налогов, сборов и иных обязательных платежей в региональный бюджет на 0,0034800605527 %. Данная тенденция на первый взгляд противоречит мейнстриму кластерной теории, устанавливающему положительную зависимость между ростом экспорта и ростом доходов региона [42; 51]. Дополнительный же анализ показал, что выявленная ситуация восходит к политическим процессам, связанным со стремлением федеральных органов власти ограничить вывоз из России грубо обработанных или необработанных лесоматериалов ценных лиственных и хвойных пород, увеличив тем самым деревообработку на территории страны1.

Действуя в системе этой политики, федеральные органы власти в 2011–2019 гг. снижали ставку по налогам и сборам (в том числе содержавшим региональный компонент). Аналогичные меры в поддержку федеральной политики были реализованы на региональном уровне2 . Кроме того, в структуре самого деревообрабатывающего сектора сравнительно широко распространены незаконные схемы снижения налоговой нагрузки, восходящие к интеграции в цепочки создания стоимости фирм-однодневок [52]. Условия кластера, способствующие развитию вертикальной интеграции, во многом симплифи-цируют данный процесс.

Совместное действие этих факторов определяет зависимость, при которой деревообрабатывающему комплексу выгоднее поставлять продукцию на внутренний рынок, а рост экспорта снижает доходы от поступления сборов, налогов и обязательных платежей.

Влияние кластера на показатель «экспорт в фактически действовавших ценах, в дол.» ( Y 6) описывает следующее уравнение:

lY 6 = 0,0000988 x C 1 + 0,0077723 x X 2 +

+ 0,0003301 x C 3 + 0,3649533 x lY 8.

Согласно данным этого уравнения увеличение значения мультипликатора занятости ( С 1) в году t – 1 на единицу стимулирует рост объемов экспорта на 0,00988048808808 %. Такое влияние восходит к действию эффекта кластерного мультипликатора, позволяющего создать дополнительные, экономически эффективные рабочие места. В свою очередь, это способствует росту производственного потенциала территории и, как следствие, позволяет увеличить экспорт (в году t ).

Рост значения кластерного мультипликатора доходов ( X 2) в году t на единицу детерминирует рост объемов экспорта в году t на 0,78025827282868 %. Следует предположить, что данная закономерность восходит к эффекту замещающего потребления. Так, часть потребителей на внутреннем рынке, предъявляющих спрос в верхнем и среднем ценовых сегментах, отдает предпочтение зарубежным товарам, рассматривая их как более качественные [53]. Очевидно, что рост доходов стимулирует этих потребителей снизить спрос на отечественные товары и увеличить спрос на импортные аналоги. Это обстоятельство вынуждает производителей изменить свое предложение на внешнем и внутреннем рынках. Вместе с тем, как свидетельствует полученный в ходе эконометрического моделирования коэффициент, такое влияние незначительно.

Воздействие кластера на показатель ВРП иллюстрирует уравнение lY7 = 0,0000285 x X1 - 0,0464597 x lC 2 -

- 0,0000367 x X 3 + 0,1415049 x lY 8.

Данная модель показывает, что при росте кластерного мультипликатора занятости (X1) на единицу ВРП в году t увеличивается на 0,0028500406129 %. В этом случае сравнительно небольшой эффект обусловлен малым вкладом деревообрабатывающего сектора в общие показатели занятости региона. Однако выявленная закономерность верно интерпретирует зависимость между изменением занятости и динамикой ВРП [47; 48].

Рост перевозок автомобильным транспортом ( lY 8) в году t на 1 % определяет рост ВРП в году t на 14,15049 %. В научных публикациях показатель «перевозка грузов по территории региона» оценивается как один из ключевых индикаторов развития транспортно-логистической системы региона. Данная сфера, в свою очередь, реализует связь между производственными единицами и потребителями [54]. Ее функционирование детерминирует ключевые показатели всех основных отраслей региональной экономики и, как следствие, ВРП [55].

Влияние индустриального кластера на показатель «перевозка грузов автомобильным транспортом» воспроизводит уравнение lY8 = -0,0000488 x C1 +

+ 0,000011 x X 3 + 0,1905967 x lA 7.

Согласно данным этого уравнения рост мультипликатора занятости на одну единицу в году t – 1 ( С 1) ведет к снижению индикатора «перевозка грузов автомобильным транспортом» в году t на 0,0000488011907394 %. Данная зависимость может быть интерпретирована через призму следующего механизма. Действие кластерного мультипликатора занятости снижает безработицу в регионе, вследствие чего наблюдается рост доходов населения [56]. Рост доходов стимулирует рост спроса на бензин и, как следствие, определяет рост цен на него [57]. Увеличение цен на бензин способствует снижению объемов перевозок грузов автомобильным транспортом. Вместе с тем, как показал проведенный анализ, это снижение незначительно.

Увеличение ВРП ( lA 7) в году t – 1 на 1 % определяет рост перевозок автомобильным транспортом на 19,05967 %. Данная закономерность может быть объяснена исходя из сути ВРП как основного обобщающего индикатора развития экономической деятельности территории. Соответственно, рост экономической активности на территории региона определяет рост грузооборота в ее границах, в том числе на автомобильном транспорте.

Рассмотрим влияние региона на функционирование индустриального кластера (табл. 7).

Таблица 7. Результаты оценки влияния региона на функционирование индустриального кластера

Table 7. Assessment results of region influence on an industrial cluster

1. Результаты регрессионного анализа влияния региона на показатель «специализация кластера»

Показатель		Коэффициент	Driscoll–Kraay standard errors	t	P >  ItI	Нижние 95%	Верхние 95%
lY 10	X 4	–0,0091837	0,0166531	–0,55	0,596	–0,0480	0,02920
	lB 2	–0,0491443	0,0189546	–2,59	0,032	–0,0930	–0,00540
	lX 6	0,0132873	0,0063724	2,09	0,071	–0,0014	0,02798
	lY 11	0,1630813	0,0378822	4,30	0,003	0,0760	0,25040
Prob >  chi 2 = 0,0000; Within R-squared = 0,51
2. Результаты регрессионног на показатель «оборот деревооб				анализа влияния региона рабатывающих организаций»
lY 11	lB 1	–0,0266884	0,0130912	–2,04	0,081	–0,05764	0,00427
	lB 2	0,1240195	0,0593276	2,09	0,075	–0,01627	0,26431
	B 3	0,0251402	0,0318364	0,79	0,456	–0,05014	0,10042
	lA 14	0,1468866	0,0978764	1,50	0,177	–0,08455	0,37833
Prob >  chi 2 = 0,0000; Within R-squared = 0,5466
3. Результаты регрессионного анализа влияния региона на показатель «фокус кластера»
Y 12	–0,0000793	0,0000752	–0,98	0,355	–0,0002474	0,0000996	–0,0000793
	–0,0001420	0,0000376	–3,78	0,005	–0,0002286	–0,0000553	–0,0001420
	0,0092908	0,0003982	23,33	0,000	0,0083725	0,0102091	0,0092908
Prob >  F = 0,0000; Within R-squared = 0,7024
4. Результаты регрессионного анализа влияния региона на показатель «размер кластера»
Y 15	B 2	0,0000499	0,0001017	0,49	0,637	–0,0001847	0,0002844
	B 3	0,0001042	0,0000332	3,14	0,014	0,0000276	0,0001808
	Y 10	0,0056100	0,0001993	28,15	0,000	0,0051505	0,0060695

Prob >  F = 0,0000; Within R-squared = 0,6230

Как следует из табл. 7, воздействие региона на показатель «специализация кластера» может быть описано уравнением lY10 = -0,0091837 x X4 + 0,0491443 x IB 2 + + 0,0132873 x IX6 + 0,1630813 x lY 1.

В соответствии с уравнением, рост логарифма кластерного акселератора доходов ( lB 2) в году t – 1 на 1 % детерминирует снижение индикатора «специализация кластера» в году t на 5,03719084712673 %. Эта закономерность связана с тем, что рост оплаты труда на предприятиях кластера, восходящий к общему увеличению уровня оплаты труда в регионе, стимулирует кластеризованные организации снижать издержки, в том числе посредством высвобождения персонала и введения ограничений на найм новых сотрудников. Такие условия определяют уменьшение веса кластера в структуре региональных показателей занятости, вследствие чего происходит снижение показателя «специализация кластера» [58; 59].

Рост логарифма кластерного акселератора экспорта (lX6) в году t на 1 % стимулирует рост индикатора «специализация кластера» в году t на 1,3375968456872 %. В этом случае акселератор экспорта может быть рассмотрен как обобщающий показатель условий реализации внешнеэкономической деятельности в регионе.

Совершенствование этих условий определяет усиление акселеративного эффекта и стимулирует рост экспорта продукции, производимой кластером. Увеличение экспорта, в свою очередь, способствует росту числа занятых на предприятиях индустриального кластера и, как следствие, детерминирует рост индикатора «специализация кластера».

Рост показателя «оборот организаций» (без субъектов малого предпринимательства, бюджетных организаций, банков, страховых и прочих финансово-кредитных организаций) по ВЭД «Обработка древесины и производство изделий из дерева и пробки, кроме мебели» (интерпретируемого как оборот кластера) ( lY 11) в году t на 1 % стимулирует рост индикатора «специализации кластера» на 16,30813 %. В данном случае показатель

«оборот кластера» выступает в роли одного из индикаторов изменения производственного потенциала рассматриваемой территориально-экономической системы. Соответственно, рост производственного потенциала индустриального кластера выступает триггером для создания новых рабочих мест на его предприятиях. Благодаря этому наблюдается рост показателя «специализация кластера».

Воздействие региона на показатель «оборот организаций» (без субъектов малого предпринимательства, бюджетных организаций, банков, страховых и прочих финансово-кредитных организаций) по ВЭД «Обработка древесины и производство изделий из дерева и пробки, кроме мебели» иллюстрирует следующее уравнение:

lY 11 = - 0,0266884 x lB 1 +

+ 0,1240195 x IB 2 + 0,0251402 x x B 3 + 0,1468866 x lA 14.

Как следует из представленной модели, увеличение кластерного акселератора занятости ( lB 1) в году t – 1 на 1 % стимулирует снижение показателя «оборот организаций» (без субъектов малого предпринимательства, бюджетных организаций, банков, страховых и прочих финансово-кредитных организаций) по ВЭД «Обработка древесины и производство изделий из дерева и пробки, кроме мебели» в году t на 2,70477248268806 %. Подобная ситуация в научной литературе интерпретируется через призму снижения эффективности труда [60].

В общем случае сложившаяся конъюнктура открывает широкие возможности для создания новых рабочих мест. Вместе с тем подобные рабочие места в случае их появления ведут к избыточности персонала и, как следствие, снижению эффективности кластеризованных организаций. В итоге оборот организаций, включенных в кластер, снижается.

Рост кластерного акселератора доходов (lB2) в году t – 1 на 1 % стимулирует рост показателя «оборот организаций» (без субъектов малого предпринимательства, бюджетных организаций, банков, страховых и прочих финансово-кредитных организаций) по ВЭД «Обработка древесины и производство изделий из дерева и пробки, кроме мебели» (в году t) на 12,40195 %. Даная закономер- ность, судя по всему, отсылает к системе мотивации персонала. Рост уровня оплаты труда в регионе стимулирует рост оплаты труда на предприятиях кластера. Исходя из сильного расхождения зарплатных ожиданий работников с реальной ставкой оплаты труда3, рост вознаграждения оказывает сильный мотивирующий эффект, в результате чего растет производительность труда и, как следствие, оборот кластеризованных организаций.

Модель влияния региона на показатель «фокус кластера» описывает уравнение

Y 12 = - 0,0000793 x X 4 - 0,000142 x x X 5 + 0,0092908 x lY 15.

В соответствии с данными модели увеличение кластерного акселератора оплаты труда ( X 4) в году t на одну единицу детерминирует снижение показателя «фокус кластера» на 0,01420100824772 единицы. Данная зависимость может быть интерпретирована следующим образом. Акселеративные эффекты, связанные с ростом общего уровня оплаты труда в регионе, ведут к росту оплаты труда на предприятиях кластера. Исходя из того, что показатель «фокус кластера» рассматривает влияние территориально-экономической системы в регионе через плоскость рынка труда, снижение значений этого показателя закономерно. Следует отметить, однако, что в рассматриваемой модели оно незначительно.

Увеличение индикатора «размер кластера» на 1 % ведет к росту фокуса кластера на 0,9334093455394 единицы. Механизм данной зависимости также представляется очевидным, поскольку основывается на прямой однонаправленной зависимости между размером индустриального кластера и уровнем его влияния в регионе.

Влияние региона на показатель «размер кластера» воспроизводит следующая модель:

Y15 = 0,0000499 x B2 + 0,0001042 x xB3 + 0,00561 x Y10.

В соответствии с полученной моделью, рост кластерного акселератора экспорта ( B 3)

на 1 единицу в году t – 1 стимулирует рост показателя «размер кластера» в году t на 0,01042054290086 единицы. Данная зависимость имеет следующее объяснение. Увеличение регионального экспорта может быть рассмотрено как прямое следствие улучшения сложившихся в регионе условий для реализации внешнеторговой деятельности. Это изменение стимулирует экспорт кластерной продукции, выступая одним из значимых триггеров развития территориально-экономической системы.

Рост индикатора «специализация кластера» ( Y 10) в году t на 1 единицу определяет рост «размера» анализируемой территориально-экономической системы на 0,56257655177303 единицы. Подобная зависимость технически является закономерной. Математически же коэффициент специализации иллюстрирует меру, в которой индустриальный кластер на своих предприятиях концентрирует специалистов в определенной сфере на региональном уровне.

Индикатор размера кластера позволяет рассматривать данные о занятости в федеральном масштабе. Исходя из этого рост регионального показателя концентрации кластера влияет на его размер в масштабах страны.

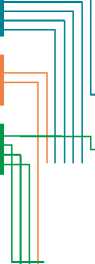
Проведенный регрессионный анализ влияния индустриального кластера на социальноэкономическое развитие региона (см. табл. 6) и воздействия региона на функционирование индустриального кластера (см. табл. 7) позволил получить набор коэффициентов, иллюстрирующих общие закономерности интеракции региона и деревообрабатывающего кластера, действующие во всех регионах страны (закономерности федерального уровня). Эти коэффициенты были введены в структуру «Системно-пространственной модели взаимовлияния региона и кластера» (см. рис. 1), что дало возможность сформировать «Общую модель взаимовлияния региона и кластера с позиции системно-пространственного подхода» (рис. 2).

Показатели влияния региона на функционирование индустриального кластера

Влияние индустриального кластера на социально-экономическое развитие региона

Мультипликатор занятости

Мультипликатор доходов

Мультипликатор экспорта

Коэффициент специализации кластера

-0,0091837 (Х4, незнач.)

-0,0491443 (/52)

0,0132873 (й'6)

0,000049 (A l)

0,0000189 (Cl)

-0,0000348 (C3)

-0,0000283

(.¥3, незнач.)

1 Показатели влияния । । кластера на социально- ] экономическое развитие региона ।

ВРП на душу населения

Начисление и поступление налогов и сборов в консолидированные бюджеты субъектов РФ

Оборот деревообрабатывающих организаций

0,0000765 (Cl)

Фокус кластера

Размер кластера

КЛАСТЕР

-0,0266884 (/51) 0,1240195 (/52) 0,0251402

(53, незнач.) -0,0000793 (Х4, незнач.)

-0,000142 (Х5)

0,0001042 (53)

0,0000499 (52, незнач.)

Кластерный акселератор доходов

Кластерный акселератор занятости

Кластерный акселератор экспорта

0,00777 (A2)

0,0000285 (XI)

-0,04646 (IC2, незнач.)

-0,0000367

(АЗ. незнач.)

-0,0000488 (С1)

0,000011 (СЗ, незнач.)

Влияние региона на функционирование индустриального кластера

Экспорт

ВРП

Перевозки грузов автомобильным транспортом

РЕГИОН

Рис. 5. Общая модель взаимовлияния региона и деревообрабатывающего кластера с позиции системно-пространственного подхода

Fig. 5. A general model of a woodwork cluster and a region mutual influence: system and spatial approach

При использовании полученных коэффициентов данная модель отражает силу и направление влияния (положительное или отрицательное) по каждому из трех кластерных мультипликаторов и трех кластерных акселераторов. Дополнительно в модели приведены обозначения переменных из уравнений, перед которыми стоят коэффициенты, в соответствии с их маркировкой, установленной в табл. 5. Это позволяет определить, к какому периоду относится переменная ( t или t – 1), и, соответственно, указывает на наличие или отсутствие временного лага при наступлении эффекта.

На практике предложенную модель следует применять вместе с комплексом полученных эконометрических уравнений, так как они, с одной стороны, дополняют друг друга, а с другой – выполняют принципиально разные функции. Например, комплекс уравнений открывает возможности для реализации прогнозирования и количественной оценки эффектов, возникающих вследствие взаимодействия двух территориально-экономических систем.

Общая модель взаимовлияния региона и кластера с позиции системно-пространственного подхода позволяет реализовать компаративный анализ эффектов кластерного мультипликатора и кластерного акселератора, выявив тем самым проблемные области, где наблюдается отрицательное влияние, и предложить необходимые корректирующие действия.

Проведем такой анализ для деревообрабатывающих кластеров. Из полученной модели следует, что рост значений мультипликатора занятости может привести к тому, что через год акселератор занятости на уровне 2 % окажет отрицательное воздействие на оборот деревообрабатывающих кластеров. Основная причина – снижение эффективности труда.

Динамика мультипликатора доходов со-направлена динамике акселератора доходов. Рост последнего имеет положительное воздействие на оборот организаций деревообрабатывающего кластера на уровне 12 %. В то же время этот эффект способствует снижению «коэффициента специализации» на 4 %. Подобное снижение иллюстрирует сокращение возможности деревообрабатывающего кластера концентрировать на своих пред- приятиях лучших специалистов, а также при росте кластерного акселератора доходов стимулирует снижение «фокуса кластера», отражающего уровень влияния рассматриваемой территориально-экономической системы в регионе. Однако такое снижение будет незначительным (на уровне 1 %).

Рост мультипликатора экспорта стимулирует рост акселератора экспорта. Последнее обстоятельство позволяет кластеризованным предприятиям расширить наем квалифицированного персонала, вследствие чего растет значение «коэффициента специализации». Одновременно происходит рост значения кластера в федеральном масштабе (показатель «размер кластера»).

Данные преобразования открывают для кластера потенциальную возможность реализации крупных проектов. Соответственно, деревообрабатывающий кластер в общем случае стремится к развитию акселератив-ных эффектов, связанных с экспортом.

Вместе с тем развитие кластерного акселератора экспорта стимулирует развитие одноименного кластерного мультипликатора, а это (как было показано) снижает объем налоговых поступлений в бюджет региона. В масштабах регионального ВРП такое снижение относительно мало ввиду небольшого вклада отрасли в экономку субъекта РФ. Однако на уровне вклада вида экономической деятельности представленное снижение может выглядеть значительным.

Проведенный в рамках модели анализ показывает, что одна и та же система «кластерный мультипликатор – кластерный акселератор» генерирует как положительные, так и отрицательные эффекты влияния индустриального кластера на социально-экономическое развитие региона и (или) эффекты воздействия региона на функционирование индустриального кластера. Представленная модель за счет коэффициентов показывает возможные варианты такого влияния, в то время как итоговый эффект зависит от специфики регионального контекста (ее иллюстрирует значение переменной, воспроизводящей кластерный мультипликатор или акселератор), а также от системы мер кластерной политики, реализованной на территории субъекта РФ в определенный период.

ЗАКЛЮЧЕНИЕ

В рамках данного исследования реализована оценка взаимовлияния региона и индустриального кластера. Для ее осуществления в первой части работы проведен концептуально-теоретический анализ, позволивший описать шесть сложившихся в научной литературе подходов к интерпретации индустриального кластера и четыре методики идентификации подобных структур.

Исследователи, реализующие оценку воздействия кластера на регион или региона на кластер, комбинируют в своих исследованиях существующие методики и подходы, формируя концептуальные системы «методика – подход». При этом адаптация конкретной методики под специфику теоретического подхода происходит через призму формирования системы индикаторов оценки.

Анализ таких концептуальных систем показал, что они акцентируют внимание либо на территориально-географической стороне индустриального кластера, либо на его социально-экономическом измерении. Вместе с тем с позиции современной науки промышленный кластер несет в себе сразу два этих начала. Соответственно, использование существующих концептуальных систем не позволяет воспроизвести полную картину влияния.

Для устранения выявленной проблемы было предложено разработать новую концептуальную систему, основанную на интеграции статистической методики и авторского системно-пространственного подхода, где проблема двух измерений индустриального кластера ранее была решена.

Новая концептуальная система позволила реализовать оценку влияния деревообрабатывающего кластера на социально-экономическое развитие региона и влияния региона на функционирование деревообрабатывающего кластера, описав их интеракцию через призму трех кластерных мультипликаторов (занятости, доходов и экспорта), а также трех кластерных акселераторов (занятости, дохода и экспорта). На основе результатов регрессионного анализа построена модель, которая воспроизводит общие для всех регионов закономерности интеракции региона и деревообрабатывающего кластера, намечая «узкие места», в которых возможно возникновение как положительных, так и негативных эффектов.

Конечный характер влияния во многом зависит от регионального контекста (который в рамках эконометрической модели отражают переменные, воспроизводящие значения кластерных мультипликаторов и акселераторов), а также от конкретных мер экономической и кластерной политики, реализуемой на территории субъекта РФ.

Работа с региональным контекстом в разрезе исследования интеракции региона и кластера составляет отдельный научный вопрос, сущность и проблематику которого предполагается раскрыть в наших следующих научных публикациях.