Оценка значений температуры в трибосопряжении в условиях граничного и смешанного режимов трения

В ряде случаев при трении в среде смазочных материалов высокой вязкости, в частности, пластичных смазочных материалов, по схеме «палец по диску» площадка контакта может быть разделена на две части: 1. участок смешанного трения в начале контакта с коэффициентом трения f1 ; 2. участок граничного трения с коэффициентом трения f2 > f1 , расположенный ближе к концу контакта. Увеличение коэффициента трения по длине контакта в этом случае обусловлено уменьшением толщины смазочного слоя в связи с «размазыванием» изначально сформировавшегося слоя смазки и затрудненным пополнением образовавшегося дефицита смазочного материала из валиков смазочного материала со стороны боковых участков индентора (пальца). Для оценки значений температуры в трибосопряжении в этих условиях в первом приближении предлагается физическая модель контакта, представленная на рис. 1. Разумеется, в реальных условиях контактного взаимодействия граница между участками 1 и 2 имеет нечеткий, «размытый» характер, а значения коэффициентов трения f2 и f1 являются средними значениями на выделенных двух участках.

Полосовые источники тепловыделения с постоянной поверхностной плотностью q_s1 и q_s2 считаем быстродвижущимися, т.е.

Pe  '——> 8_10 .

d 2

Это означает, что распространением теплоты перед движущимися источниками можно пренебречь и считать, что теплота распространяется только по нормали к поверхности контакта.

Такое допущение позволяет представить полупространство (тело 2) как пакет полуограниченных пластин малой толщины, имеющих адиабатическую изолированную боковую поверхность, и свести задачу к классу задач одномерной нестационарной теплопроводности.

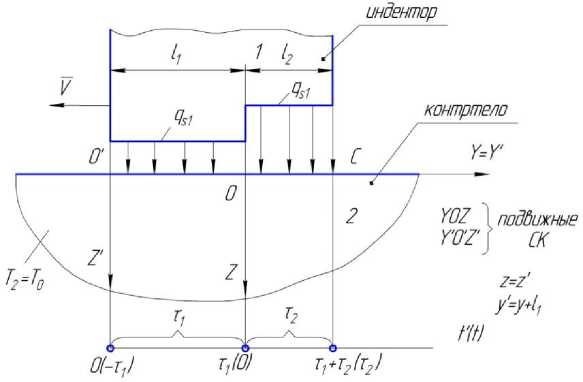
Рис. 1. Формализованная физическая модель контакта

Для описания «моментального снимка» температурного поля в контртеле 2 (неподвижное полупространство) в подвижных системах координат YOZ и Y’O’Z’ , который будет воспроизводиться в каждый текущий момент времени t’(t) при установившемся трении, в этом случае можно использовать решение для температурного поля в полупространстве одного измерения под действием единичного теплового импульса с постоянной поверхностной плотностью q , действующего в течение времени т и [1]:

• 1)    Фаза нагрева (0 < z < го , 0 < t < ти)

,   .   2qVot        _z_ .

^L(Z,⁴   _Л   ^^VOt ;

• 2)    Фаза охлаждения (0 < z < го ,t >  т_и)

T(z’tj = VW[vt 1 erfC 2 Vat - V^-W 1 erfc 27stt=T=] ’ где i erfc и = J” erfc x dx = ^ e-2 — u erfc и , erfc u = 1 — erf и = -2j” e-2 dx .               (3)

Таким образом, решение задачи нестационарной теплопроводности по определению температурного поля в контртеле 2 (неподвижное полупространство) будет иметь вид:

• 1)    Зона смешанного трения O’O (0 < t ‘ < Т 1 = ^ 1 ; 0 < у ' <  1 1 ;

q = Qsi=X fiPV)

2q_s i Ja 2^-

Z 2Ja2?

+ T o =

T2(y',z) =------i erfc

^ 2

2 ^{4 51}^ [-L e 4«2У' ——^ erfc     ] + _T .

-                                              0

• 2)    Зона граничного трения OC (1 1 < t' <1 1 + 1 2 = ~~ 2 ; 1 1 < у ' <  1 1 + 1 2 ;

q = qS2 =xf2pv).

Температурное поле в этой зоне определяется как суперпозиция полей от двух движущихся полосовых источников с поверхностными плотностями теплового потока q s1 и q s2

T2(y',Z) = /i(y',z) + l2(y',z) .

W,z)

_ 2Q s1 V^ 2

= Л₂

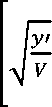
i erfc

z 2J“2^

y'-k л] V

i erfc

Ji-1]

+ To =

2Q s1 V^ 2

Л

{J^l^l^e

z²V — 4d ₂ y'

z ^2J“ 2V

erfc

z

2J^25

l- jekL

V Тя

z²V e ^4a2⁽y -^1) —

z

2J^ZI

^erfc 2JSs| ^} ■

^2(y',Z)

^s2^2^--1

i erfc

2J^ 2^^-

= ^^sS'E 1л e-^Skl — -^= erfc ^=

^X 2    ⁴⁵        2р ' ^-1   2^Й

Температура в точке О на поверхности контакта (условная граница между зонами смешанного и граничного трения)

T2(h,0)= 2^21^ + To . (i erfc 0 = 1)             (8)

A ^ yTtV                                V TT

Температура в точке C на поверхности контакта (максимальная поверхностная температура)

^Tmax = ^T 2 G1 + ^ 2 ,0) = .^^ [Q sl (^ 1 + ^ 2 - ^V 2 ⁾ + Q s2 V^ 2 ] + ^T 0 .    (9)

График распределения температуры на поверхности контакта представлен на рис. 2.

Температурное поле в теле 1 (индентор), рассматриваемом как полуограниченный стержень без тепловой изоляции (стационарный тепловой режим, координата z направлена от поверхности контакта вглубь тела) [2]

T1(Z) = (Tk - To) exp (-VbI D + To,            (10)

где Tk = Ti(0).

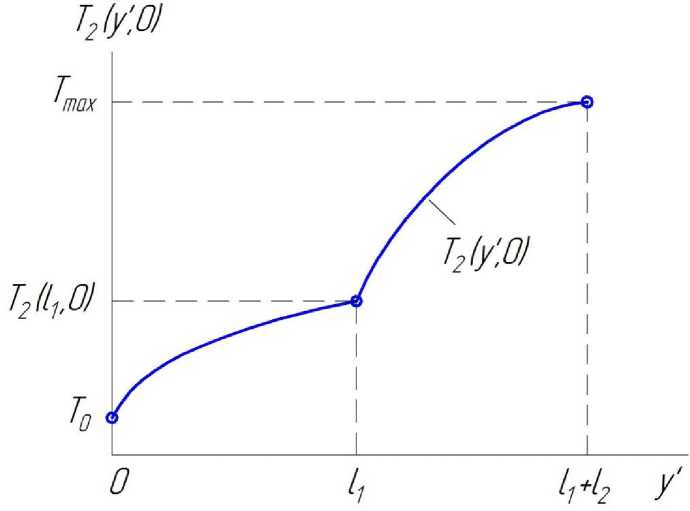
Рис. 2. Распределение температуры на поверхности контакта

Первая производная от температуры по координате

^^(z)      VbI                      z

— =- —(Tk-To)exp(-VBl -).

Средняя поверхностная плотность теплового потока, направленного от поверхности контакта в индентор

Чи = -^^ = 211чТк-То) = (1- x)h>v,

Г   f1h+f 2 l 2

где f = 4+T .

Полагая T0 = 0 , получаем

Tk =

^^^^

6рУ/(1~х)

Х1ЛЯ

Для определения неизвестного коэффициента распределения теплового потока х используем балансовое уравнение T_k = T 2 (Z₁,0) (условие неразрывности температурного поля), которое при Т₀ = 0 имеет вид

8рУ/(1—х)2Х/ 1 РУ^ а- 2 1 1

.

Х 1 4В1      x₂^sy

Решая это балансовое уравнение, получаем

Л 1 / 1 ¹   Гс22р1В1'\

z = (1 + 25; у s^—)

Таким образом, получив зависимость для расчёта коэффициента распределения теплового потока на площадке контакта индентора с контртелом χ, мы определили последнюю неизвестную величину, входящую в формулы для оценочного расчёта температурного поля в контактирующих телах 1 и 2, а также распределение поверхностной температуры на площадке контакта. Задачу теплофизического анализа процесса трения для случая, когда площадка контакта может быть разделена на две части: 1. участок смешанного трения в начале контакта с коэффициентом трения f1 ; 2. участок граничного трения с коэффициентом трения f2 > f1 , расположенный ближе к концу контакта, можно считать решенной. Полученные расчётные зависимости являются замкнутыми и не содержат неизвестных величин.

Обозначения

1 1(2) — длина участка смешанного (граничного) трения на поверхности контакта;

Pe - критерий Пекле;

• V - скорость скольжения;

а₂ - коэффициент температуропроводности материала контртела (тела 2);

t’(t) - текущее время контактного взаимодействия, привязанное к подвижной системе координат Y’O’Z’ (YOZ) ;

т 1( ₂ ) - полное время контактного взаимодействия на участках смешанного (1) и граничного (2) трения;

q_s1 (2) — поверхностная плотность теплового потока, направленного от поверхности контакта в контртело на участках смешанного (1) и граничного (2) трения;

p - нормальное давление на контакте;

• X - коэффициент распределения теплового потока на контакте между индентором и контртелом;

T 0 - начальная температура (температура окружающей среды);

f1(2) - средний коэффициент трения на участках смешанного (1) и граничного (2) трения;

/ - средний коэффициент трения по всей поверхности контакта;

qu - поверхностная плотность теплового потока, направленного от поверхности контакта в индентор;

T₁ ( ₂ ) - температура в инденторе (1) и контртеле (2);

^1(2) - коэффициент теплопроводности материала индентора (1) и контртела (2);

Bi - критерий Био;

а - коэффициент теплоотдачи на боковых поверхностях индентора;

δ – отношение площади поперечного сечения индентора к периметру сечения (характерный линейный размер).

erf и = -^f ^ e ^-x 2 dx - функция ошибок Гаусса.

Выводы:

• 1.    Решена в первом приближении задача теплофизического анализа процесса трения для случая, когда площадка контакта может быть разделена на две части: 1) участок смешанного трения в начале контакта с коэффициентом трения f 1 ; 2) участок граничного трения с коэффициентом трения f₂ > f₁ , расположенный ближе к концу контакта. Полученные расчётные зависимости являются замкнутыми и не содержат неизвестных величин.

• 2.    Разработанный алгоритм расчёта температурных полей в контактирующих телах может быть представлен в виде программы для ЭВМ, что позволяет существенно ускорить проведение расчетов при решении конкретных задач теплофизического анализа процессов трения и обработки лезвийным инструментом.

• 3.    Примененная методика теплофизического анализа является, в принципе, применимой к парам трения любой конфигурации и любым технологическим системам или их подсистемам независимо от того, какие рабочие процессы осуществляются в этих системах (лезвийная обработка, обработка ППД, шлифование и т.д.).