Оценки индикаторов целой функции с отрицательными корнями

Так случилось, что будучи воспитанниками ростовской школы комплексного анализа, многие годы возглавляемой профессором Ю. Ф. Коробейником, авторы этой заметки, в разное время переехав в Москву, около пятнадцати лет назад объединили свои усилия

• ^# Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований, проект № 18-01-00236.

для изучения цикла новых, специальных задач теории роста целых функций. Аппарат целых функций является неотъемлемым инструментом при исследовании уравнений типа свертки, операторных уравнений бесконечного порядка, полных и представляющих систем, интерполяционных задач и многих других областей анализа, в которых важные и широко известные результаты принадлежат Ю. Ф. Коробейнику и его научной школе (см. [1]). Статья посвящена юбилею Юрия Федоровича Коробейника — Учителя, «заразившего» нас любовью к целым функциям.

Поздравляем Юрия Федоровича со славной датой, желаем крепкого здоровья и долгих лет творческой жизни!

1. Предварительные сведения и известные результаты

В классической теории роста целых функций давно изучается вопрос о том, как зависит скорость возрастания максимума модуля функции от закона распределения на плоскости последовательности ее корней (см., например, мемуар Э. Линделефа [2]).

Пусть f — целая функция, отличная от тождественного нуля. Будем предполагать, что f имеет бесконечно много корней и записывать их с учетом кратностей по неубыванию модулей в виде последовательности Л = Л f = (А _п ) П =_г Обозначим

M f (r) = max | f(z) | , r> 0.                               (1)

^{| z |} = r

Одной из основных асимптотических характеристик логарифма максимума модуля (1) целой функции f порядка p E (0, + то ) является ее тип, который определяется по формуле

. х             ln Mf (r)/ .

^P(f) = Jim            .

r >  • ^

При том же порядке ρ вводят верхнюю и нижнюю плотности последовательности корней Л = (A n )^ ! обычным образом:

Ар(Л) = lim —, А р(Л) = lim —-.(3)

n →∞ | λ _n |                _{n →∞} | λ _n |

Важной проблемой теории целых функций является задача о нахождении соотношений между характеристиками (2) и (3). Так, еще Ж. Валирон [3; ч. 2, II] показал, что в общем случае Л С C при заданном значении верхней плотности А р (Л) = в > 0 справедлива оценка

» , (f) » -•                                     (4)

ρe

Известно, что для любого p >  0 оценка (4) достигается [4; гл. 4, § 1], т. е. существует целая функция f, для которой в (4) имеет место равенство. При дополнительной информации о нижней плотности А р (Л) ^ а, где a E [0,в], оценка может быть усилена:

° P f ) >  p ^exP | a - 1^.                           ⁽⁵⁾

По поводу результата (5) см. монографию [5; с. 16] и обзор [6; § 2]. В то же время, благодаря исследованиям Ж. Валирона, А. Данжуа, а затем А. А. Гольдберга, была найдена точная оценка сверху для величины (2) через верхнюю плотность А р (Л) = в > 0

множества корней Л С C. Эта оценка довольно сложна, но в случае р Е (0, 1) она упрощается к виду

O р ^f ) < — -                           (6)

sin пр

Укажем, что (6) достигается на целых функциях с последовательностью отрицательных (или лежащих на фиксированном луче arg z = 9) корней, имеющей плотность

n

^А р ^(л) = Иш —— = ^в,                        ⁽⁷⁾

n→∞ |λn |ρ хотя наличие плотности не является строго обязательным для справедливости равенства в (6) (подробности см. в [6]). Уже здесь начинает проявляться существенное влияние ««геометрии» расположения Л в C на характер подобных задач.

Переход к целым функциям f с нулями на луче (для определенности считаем, что Л = Л f С ( —то , 0)) приводит к существенному уточнению результатов (4), (5). Дадим формулировку соответствующего утверждения, полученного в работе [7].

Теорема A. Пусть р Е (0,1), в > 0, а Е [0,в]- Тогда для любой целой функции f порядка р с последовательностью отрицательных корней Л = Л f верхней плотности А р (Л) = в и нижней плотности А р (Л) ^ а выполняется неравенство

a

πα               βa-ρ - ατ-ρ ор(f) >  --+ max -------------dr-                    (8)

^{р 7} sin пр   a> 0    J        T + 1                            ^{v 7}

а ( а/в ) 1 / ^p

Равенство в (8) достигается на некоторой целой функции f с последовательностью отрицательных корней Л = Л f такой, что А р (Л) = в и А р (Л) = а .

Только два «предельных» случая теоремы A были известны на момент ее появления: а = в и а = 0. В первом случае, с учетом оценки Валирона (6), получаем формулу

O р ^{( f} ) =

πβ

, sin пр

позволяющую вычислять тип целой функции с измеримой последовательностью отрицательных корней. Во втором случае из неравенства (8) извлекается принадлежащая А. Ю. Попову [8] точная оценка снизу для типа целой функции я ln(a + 1 W) > вmax----- a>0    ар

при ограничениях р Е (0,1), Л = Л f С ( —то , 0), А р (Л) = в.

Еще более сложным образом локализация корней функции сказывается в задаче о наименьшем типе при переходе от луча к углу фиксированного раствора. Такое развитие теорема A получила в работе [9], основной результат которой состоит в следующем.

Теорема B. Пусть заданы числа р Е (0,1), в > 0, а Е [0,в], 9 Е [0,п/2]. Тогда для любой целой функции f порядка р с последовательностью корней Л = Л f , расположенной в каком-либо замкнутом угле Г д раствора 29, при ограничениях А р (Л) = в, А р (Л) ^ а, выполняется неравенство

a

. па „            Г    (ва-р — ат-р)(т + cos 9) ,, .

Op(f) ^ ----- cosр9 + max -----5------------------dr.(10)

• ри7 sin пр p    a>0   J        r2 + 2r cos 9 + 1

a(a/e) 1/^p

Равенство в (10) достигается на некоторой целой функции f с последовательностью корней Л = Л f , расположенной на сторонах угла Г д так, что А р (Л) = в и А р (Л) = а.

Очевидно, что теорема A следует из теоремы B при 9 = 0. Подставляя в оценку (10) значение а = 0 и вычисляя интеграл, получим доказанное в [10] незадолго до теоремы B точное неравенство

,,(f) >  ^в max ^{a + 2a} cos ⁹ + 4. (11)

^PV1' 2 a> 0 a P ^v ’

Здесь Л = Л f С Г с фиксированным раствором 29 € [0, п], а А р (Л) = в с заданными параметрами р € (0,1), в > 0. Кроме того [6; заключительная часть §7], если целая функция f является экстремальной в оценке (11) (см. также (9)), то нижняя плотность (при показателе р) множества корней Л f необходимо равна нулю. Дополнительную информацию, связанную с результатами этого раздела, см. в обзорах [6, 10].

Несмотря на прозрачность постановок, задачи указанного направления, учитывающие расположение корней целой функции, весьма трудны. В частности, распространение теорем A, B на нецелые значения р >  1 является на данный момент нерешенной проблемой даже при а = 0. В следующем разделе мы дадим возможный подход к решению этой проблемы, основанный на изучении индикатора целой функции. Наряду с новыми утверждениями, для полноты картины будут представлены также недавние результаты о нижнем индикаторе из статьи [11]. Насколько нам известно, обсуждаемые задачи не охвачены этапными исследованиями А. А. Гольдберга 60-х годов прошлого века, мощной теорией предельных множеств В. С. Азарина (см. [12; гл. 1–3]), а также недавними совместными работами К. Г. Малютина, М. В. Кабанко, Т. И. Малютиной [13, 14].

2. Индикаторы целой функции с отрицательными корнями

Напомним определения двух стандартных характеристик роста целой функции, учет которых дает в простых терминах «границы» ее асимптотического поведения на лучах комплексной плоскости.

Для целой функции f ^ 0 индикатор и нижний индикатор при порядке р > 0 задаются соответственно формулами hp(f,9)

ln |f (reis)| lim ---------- r^+^    rp

h _P (f, 9) = sup lim

Eo r^+^,r/Eo ln |f (reis)|

в которых аргумент 9 € ( — п, п]. Супремум во второй формуле берется по всем множествам E o С (0, + то ) нулевой относительной меры (подробную информацию об индикаторах целой функции см. в [4; гл. I, § 15; гл. II, § 1], [15, 16]).

В этом разделе рассматриваем целую функцию f положительного нецелого порядка ρ и нормального типа с последовательностью отрицательных корней Л = Л f = (А _п ) П =1 , где

0 > A i >  A ₂ ^ ... ^ A n >  ..., lim A n = —то . (13) n →∞

Для такой функции f имеем hp(f,9) h P(f,n)

= lim          ,     9 € r^+^

= sup lim     ^ln ' f - r ) ,

E o r ^ + ^ ,r/E o

( — п, п),

что при 9 Е ( - п, п) приводит к полному единообразию записи в определении пары «индикатор — нижний индикатор», характеризующей «радиальное» поведение | f | в плоскости с разрезом по отрицательному лучу.

Если последовательность (13) является измеримой, т. е. подчинена (7), то индикатор и нижний индикатор функции f совпадают и однозначно вычисляются по формуле

πβ hp(f, 9) = hp(f, 9) = sin пр cos р 9, 9 Е (-п, п]

(см., например, [4; гл. I, § 17, теорема 25; гл. II, § 2], [17; гл. 7]). Если же последовательность корней неизмерима, т. е. А р (Л) < А р (Л), то подобные формулы неизвестны, так как индикаторы функции, вообще говоря, не могут быть вычислены через плотности множества ее корней. Возникает вопрос о границах изменения индикатора и нижнего индикатора функции, если зафиксированы верхняя и нижняя плотности (3) последовательности (13).

Изучаем самую «нерегулярную» ситуацию, когда верхняя и нижняя плотности максимально различаются:

Ар(Л)= в> 0, Ар(Л)=0.(16)

Без ограничения общности можно считать, что функция f задана каноническим произ- ведением рода p = [р], т. е.

'f (z)= П (1 -     ,z

(p = 0),

(p Е N).

n=1 '

/ ^(z)= Д (1 ^-    ) exp |   + ... + . |, z ^{Е C}

Используя для (17) интегральное представление [17; теорема 7.2.1], запишем

⁺ ^

e =            Кр(т, 9) dr. r> 0, 9 Е (-,.,),(18)

гр J где nA(t) = ^^ 1 = max {n : |An| < t}(19)

| A „ |

— считающая функция корней f ,

, x           тy-1(t cos ((p + 1) 9) + cosp9)         zz x

Kp(T9) = (-l)P     * T 2 ,z. cos 9 +1    P ' • 9 Е пп(2

Здесь и ниже приняты обозначения p = [р], y = {р} = Р - Р соответственно для целой и дробной частей числа ρ. Функцию (20) называем ядром интегрального представления (18). Четность ядра по переменной θ влечет равенства hp(f, -9) = hp(f,9), hp(f, -9) = hp(f,9), 9 Е (-п,п), и позволяет ограничиться значениями 9 Е [0, п). (Укажем, что не входящее в формулы (18), (20) значение 9 = п соответствует отрицательному лучу, на котором расположены корни функции f, а там ее поведение нуждается в отдельном рассмотрении.) При фиксированных p, 9 и возрастании т от 0 до +^ возможны две ситуации: ядро сохраняет постоянный знак; ядро меняет знак при переходе через точку т* > 0, где

,                cos p9                                         , .

^т * = ^т * ⁽p,⁹⁾ =-- .                             (21)

cos((p + 1)9)

В этой связи вводим следующие множества, по факту зависящие только от p Е N U { 0 } , которые для удобства ссылок назовем индикаторными множествами :

Г/ = {9 Е [0, п) : К _р (т, 9) > 0 при всех т Е (0, + то )},

Г Р- ) = {9 Е [0, п) : К р (т,9) < 0 при всех т Е (0, + то )},

Г Р ± ) = {9 Е [0, п) : т * >  0; К р (т, 9) > 0 при т Е (0,т * ), К р (т, 9) < 0 при т Е (т * , + то )},

Г Р Т ) = {9 Е [0, п) : т * >  0; К р (т,9) < 0 при т Е (0,т * ), К р (т, 9) > 0 при т Е (т * , + то )}.

Для любого целого неотрицательного p эти множества не пересекаются и таковы, что

[0, п) = г р⁺⁾ и г Р ^{- )} и г Р ± ) и г; .

Например, если р Е (0,1), то p = 0, 7 = р, и по формулам (20), (21) имеем

К р (т,9) =

т ^{р 1} (т cos 9 + 1) т ² + 2т cos 9 + 1,

^т * = ^т * ^(0,9) = - cos-9,

откуда

' ' = [0,2 ], Г ^- = 0, Г^ = ( П ,п), Г^ = 0.            (22)

Формулы (22) отвечают ««начальному» значению p = 0, которое в определенном смысле является особым. Как выглядит результат в общем случае? Из определения (20) следует, что для ответа на вопрос достаточно при заданном p Е N выяснить поведение на положительной полуоси т > 0 величины ( —1)р(тcos((p +1)9) + cosp9) с параметром 9 Е [0,п). Кропотливые вычисления позволяют дать полное описание индикаторных множеств, которое выглядит по-разному для четного и нечетного (относительно индекса p) случаев. Не приводя здесь общего, весьма объемного утверждения, отметим только, что для p = 1 и p = 2 имеем соответственно г1+) = [2,3л], г1-) = Н], Г?) -(*„).  Г?) - (1,2),     (23)

= [0, п ] U [7, 5 п] , ^Г 2 ^{- )} = [ п , п ].

7?) = (п- п) U (5Е,п), Г2Т) = (п, 3п)- с заметным усложнением структуры по сравнению с (22). Пользуясь моментом, укажем, что при записи формул (22)–(24) исправлены неточности, допущенные в [11; п. 2].

Перейдем теперь к основным результатам работы.

Теорема 1. Пусть f — целая функция порядка р Е (0, +то) \ N с последовательностью Л отрицательных корней, подчиненной требованию (16), т. е. такой, что Ар(Л) = в > 0, А р(Л) = 0, и p = [р]. Тогда индикатор (12) функции f удовлетворяет неравенству hp(f,9) > 0, 9 Е (-п, п],

причем hp(f,9) = 0, 9 G ГР-).(26)

Нижний индикатор (14) функции f удовлетворяет неравенству hp(f,9) < 0, 9 G (-п,п],(27)

причем hp(f,9) = 0, 9 G ГР+).(28)

• <1 Тождество (28) получено в статье [11; теорема 1]. Там же для значений 9 G ( — п,п) установлено соотношение (27). То, что (27) выполнено и в предельном случае 9 = п, не рассмотренном в [11], следует из результатов работы [18; доказательство теоремы 1] (см. также [19]), согласно которым существует (возможно, равный -∞ ) предел

• # >— h p ^(f,9) = h p ^(f,n)-

• Добавим еще, что в соответствии с [18; теоремы 1, 3 и замечание 2] справедливы формулы

ξ hp(f, п) = lim lim 1^ J -§>1—0 r>+^ r 0

- p -

¹ п л (гт ) - T ^p п л (г/т ) ,

1—T                ,

ξ hр(Лп)= limn hP(f,9) = „limn lim rP J ^ >n 0                 § >1 ° r > ■ ^ о

τ ^-p

-

¹ п л Ргт ) — т ^p п л ( г/т ) ,

1 — T             ^dT,

выражающие величины h p (f, п) ^ 0, h p (f, п) <  0 непосредственно через считающую функцию (19) последовательности корней (13). (Строго говоря, в [18, 19] изучались целые функции с положительными корнями, но это не имеет принципиального значения.)

Обоснуем теперь новые результаты (25), (26). Опуская технические детали, приведем схему рассуждений, предложенную в [11; доказательство теоремы 1] при исследовании нижнего индикатора (см. также [7]).

Для произвольных положительных чисел a, r справедлива оценка пл(гт) < Па(г) (гт)р (ат)р 1

0 < т < -, a

в которой величина

пл(г/а) Па(г) = ( / Хо (r/a)p при фиксированном а > 0 в силу (16) удовлетворяет

соотношениям

lim n a (r) = в > 0,

lim

П а (г) = 0.

Пригодится также «грубая» оценка

^ <  D- г,т> °'                    (32)

выполненная с некоторой константой D ^ в.

Сначала докажем тождество (26). Пусть 9 G гР ). Тогда Кр(т, 9) < 0 при всех т > 0, и согласно (12), (18) имеем hp(f,9) < 0, 9 G ГР-).                                   (33)

С другой стороны, зафиксировав a Е (0,1) и применив в (18) оценки (30), (32), при тех же 9 Е гР ) получим, что ln |f (rei )|

1 /a

> П а (г) a - ^p j т ^{- р} К р

a

a               +^          \

( К р (т,в) dT + ( К р (т,9) dr\.

0                  1 /a

Последующий переход к верхнему пределу при r ^ +то с учетом второго соотношения в (31) дает неравенство hp(f,9) > D

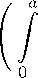
К р (т, 9) dT +

+ ^

j К р (т,9)

dτ .

1 /a

Устремляя теперь параметр a к нулю, имеем hp(f,9) > 0, 9 Е ГР-).

Для получения заявленного тождества (26) осталось сопоставить (33) и (34).

Перейдем к доказательству неравенства (25). Рассуждения достаточно провести для 9 Е Гр±) U гР^). Пусть 9 Е Гр±). Зафиксируем a Е (0, т* 1), где точка т* определена в (21). Тогда Кр(т, 9) > 0 при т Е (0, т*) и Кр(т, 9) < 0 при т Е (т*, +то). Поэтому ln |f (гег6 )|

+ ^

>/        К р (т, 9) ат.

τ ∗

На отрезке т Е [т * , 1/a] подынтегральную функцию оценим с помощью (30), а на луче т Е [1/a, + то) — с помощью (32). Последующий переход к верхнему пределу при r ^ + то с учетом второго соотношения в (31), а затем переход к пределу при a ^ 0 дают неотрицательность индикатора при 9 Е г Р ± ) . Оставшийся случай 9 Е г Р ^ ) разбирается схожим образом. >

Общие результаты теоремы 1 органично связаны с предположением А р (Л) = 0, действуют при любом фиксированном в >  0 из условия (16), но не раскрывают зависимости индикаторов от конкретного значения β верхней плотности корней функции. Это хорошо видно из приведенного краткого доказательства, где вместо точного первого предельного соотношения в (31) применялся его ослабленный вариант в форме (32).

Следующее точное утверждение — теорема 2 — получено благодаря учету информации (31) в полном объеме. Доказательство, ввиду его громоздкости, не приводим — оно будет дано в отдельной работе (часть теоремы 2, относящаяся к нижнему индикатору, уже опубликована в [11; теорема 2]). Как оказалось, результат допускает запись в той же форме, что и в (11), указывая на связь двух экстремальных задач: о наименьшем типе целой функции с корнями в угле; о наименьшем индикаторе целой функции с корнями на луче.

Теорема 2. Пусть f — целая функция порядка р Е (0, +то) \ N с последовательностью Л отрицательных корней, подчиненной требованию (16), и p = [р]. Тогда для индикаторов функции f верны точные оценки hp(f,9) > в sup {a-pIp(a,9)}, 9 Е гР+), (35)

a> 0

h p (f,6) ^ в mf {a ^{- p} I p (a,9)}, 9 E r P " > ,

где величина I _p (a,9) вычисляется по правилу

Io (a, 9) = 2 ln (a2 + 2a cos 9 + 1), pm

I _p (a,9) - 2 ln (a ² + 2acos 9 + 1) + Е ( — 1) mam cos m9, p E N.

Для произвольно заданных p E (0, + то ) \ N и в >  0 существует целая функция, которая оценки (35), (36) одновременно превращает в тождества на указанных там промежутках.

Упомянутой экстремальной функцией в теореме 2 будет каноническое произведение рода p (см. (17)), если последовательность Л = (A _n ) 0 =1 его корней выбрать так, чтобы

⁰ > ^А 1    . . .   ^А П 1 > ^А П 1 +1    . . .   ^A n 2 > . . . > ^A n k + 1    . . .   ^A n k + 1 > • • • ,

* /"О ^A n k ^- -”;                                                              (39)

А _Р (Л) - lim ,,ⁿk_lp - в > 0, lim ,^Xnk - 0.

k →∞ ^{| λ n} k ^|               k →∞ ^{λ n} k +1

Для любых p E (0, +to) \ N и в > 0 построить последовательность Л, удовлетворяющую (39), можно следующим образом:

A 1 - . . . - A n 1 - — 2,	П 1 - [2 р в];
А П 1 +1 — ••• — А П 2 —   2 ,	П 2 - [2 р в] + [2 2р в];
..., A n k -1 +1 - • • • - A n k - — 2 2    ,	..., k n k - Е [2 2 j-1 p в]; j =1
А П к + 1 - • • • - А П к +1 - — 2 2 , ...,	k +1 П к +1 - Е [2 2 j -1 р в] j =1 ...

В приведенной конструкции кратность каждой точки Ank - — 22k 1 в последовательности Л равна [22k 1рв], а длина лакуны между соседними (различными) членами Ank+1 и Ank составляет 22k 1 (22k 1 — 1). Класс подобных примеров (39) образует специальный случай последовательностей (13) со свойствами (16). Специфика последовательности (39) приводит к тому, что индикаторы функции (17) вычисляются по формулам hp(f,9)- в sup {a-pIp(a,9)}, h p(f,9} - в inf {a-pIp(a,9)}, 9 E (—п,п), (40) a>o a>o с величиной Ip(a, 9), определенной в (37). Тем самым, оценки (35), (36) из теоремы 2 точны, а фигурирующие в них выражения, распространенные с промежутков гР+), гР ) соответственно на весь интервал (—п, п), задают закон вычисления индикаторов целой функции порядка p E (0, +то) \ N с «быстрорастущей» (без учета кратностей) последовательностью модулей корней (см. также [11]).

Конкретизируем наши результаты в наиболее простом из исследуемых в работе случае, когда целая функция f с отрицательными корнями удовлетворяет ограничениям (16) при порядке p E (0,1). Можно показать (см. также [19]), что индикатор и нижний индикатор f будут непрерывными функциями аргумента 9 E (—п, п), возрастающими при 9 Е ( — п, 0] и убывающими при 9 Е [0, п) в нестрогом смысле. Индикатор hp(f,9) непрерывен также в точке 9 = п. В случае нижнего индикатора в точке 9 = п имеем обобщенную непрерывность: hp(f, 9) будет непрерывен в этой точке, если hp(f, п) > —то; в противном случае lim hp(f, 9) = hp(f, п) = —то. С учетом сказанного при всех р Е (0,1) выполнены равенства max hp(f,9) = hp(f 0),    max hp(f,9) = hp(f0);

9 e ( — n,n ]                             9 e ( — n,n ]

min h p ^(f, ⁹⁾ = h p ^(f,^п),    min h p ^(f, ⁹⁾ = h p ^{(f п) Е {—то}} U R,

9Е(— п,п ]                             9Е( — п,п ]

не зависящие от ограничений (16). Но для выделенного случая эти сведения можно существенно расширить, если собрать утверждения, заложенные в теоремах 1, 2. Учтем вид индикаторных множеств (22), а также предельные соотношения (29) при p = 0. В итоге для выбранного класса целых функций дополнительная к (41) сводная информация об индикаторе выглядит так:

'h p (f,9) >  0, 9 е( — п, — |) U (п,п);

, hp(f,9) > в SUp Mancosm), 9 е [ — п , п 1; a>0                            LJ hp(f,п) = lim lim £ ) '                 dT е [0, +то),

(11-0 r 1'X 1 0

а о нижнем индикаторе — соответственно так:

' h p^ ^ 0, 9 е(— п, — j) U (j ,п) ;

< hpU^ ^ 0, 9 Е [ — п, 2];(43)

hp(f,п)= limn lim rip } T-1 ПЛ(7--ПЛ(Г/Т) dT Е [—то, 0]. (11-0 ri+^

Отдельный интерес представляет следующая задача: при тех же ограничениях (16) найти в терминах параметров р Е (0,1), в > 0 точный диапазон изменения величин hp(f, п), hp(f,п') из формул (42), (43). Для подкласса функций с корнями (39) новые формулы (40) дают ответ hP(f,п) = 2

h P ^(f,п) = 2

lim sup

^{9 1 п — 0}a> 0

lim inf

9 1 п — 0 a> 0

ln( a ² +2 a cos 9 +1) _ a P           ^;

ln( a ² +2 a cos 9 +1) a ^{ρ            ,}

который после некоторой обработки приводится к окончательному результату ho(f, п) = в max —a------, h „( f, п) = —то.

^pu’ ^{2 p} a>2     a P      ~^p

(Совсем не очевидно, что соотношения (44) можно получить, применив известные по работе [19] заключительные части формул (42), (43). Было бы полезно с помощью (40) доказать аналоги (44) для порядков р > 1.)

Вернемся к общему классу целых функций f порядка р Е (0, 1) с последовательностью отрицательных корней, подчиненной (16). На основании соответствующих свойств индикатора из (41), (42) запишем для типа Cp(f) (см. (2)) точную, достижимую оценку снизу

° p ^f )= max асл^н h p f ^o) > ^e max ^{ln( a} + ¹⁾ 0 G ( - n,n ]                            a> 0      a ^p

.

Этот результат, полученный нами в предположении А р (Л) = 0, справедлив при любом значении А р (Л), совпадая с цитированной оценкой Попова (9).

Пусть р Е (0, + то ) \ N. Обозначим через C (р) точную нижнюю грань величин ^ p (f ), взятую по всевозможным целым функциям порядка ρ с множеством отрицательных корней Л = Л f верхней плотности А р (Л) = 1 и нижней плотности А р (Л) = 0. Тогда

C⁽р) = max ln^a+H, р ^{е (0,1)}. a> 0     а ^р

К настоящему времени формула (45) — единственный точный результат в экстремальной задаче о вычислении величины C (р). Мы посвятим этой задаче следующий раздел.

3.    Задача о наименьшем типе

В работе Попова [20] для значений функции C (р) найдены следующие границы:

2 ^{- р/2} ^ C (р) ^ 2 ^{1 - р} (1 + max lna—< 1.28 • 2 ^{1 - р} , р Е (1, 2), \ a > 2 а у

2 - р

C(р) < —, р ^Е (i,²),

+ ^

0.47 <  - У cost dt <  C (р) < 1, р Е (2, + го ) \ N.

п/ 2

Используя утверждения предыдущего раздела, можно дать новые оценки экстремальной величины C(р) при р > 1, усиливающие (46)-(48). Сейчас ограничимся простейшими приложениями полученных результатов, оставляя более глубокий анализ для отдельной публикации. Будем опираться на общую двустороннюю оценку max sup {a pIp(a,6)} < C(р) < max sup {a pIp(a,6)} ,       (49)

^р е г Р ⁺⁾ a>^{0                                   E} - r. .' . '2 p ±1 n,n l a>⁰

2p+2

действующую при всех р Е (1, +то) \ N. По-прежнему, p = [р] Е N. Величина Ip(a, 6) определена в (37). Основу соотношения (49) составляет известное свойство индикатора max hipff,^ = ^p(f),

9 E ( — п,п ]

которое ввиду специфики расположения корней f можно переписать так:

^max h p ^(f,6) = U p ^(f).

^p G [0 ,n ]

Неравенство (35) из теоремы 2 влечет оценку снизу в (49). Оценка сверху возникает благодаря примеру (39) с точным правилом (40) для вычисления индикатора, поскольку C (р) по определению не превосходит типа любой целой функции из заданного класса. При этом дополнительно учитывается соотношение (26), доказанное в теореме 1. Оно вкупе с характеристическим свойством индикатора — тригонометрической выпуклостью (см. [4; гл. I, §15, лемма 6]) — позволяет при нахождении максимума hp(f,6) на [0, п] (-)    (∓)

сразу исключить из рассмотрения индикаторные множества Г p , Г p , а также все промежутки, входящие в г Р ± ) , кроме одного — отрезка [ 2 p +2 п, п], который при p ^ ± от стягивается в точку 6 = п. Дальнейшее упрощение (49) естественно связать с исследованием на монотонность (по θ) индикатора из формулы (40). Впрочем, целесообразно отложить подробности для развернутой работы и перейти к конкретным применениям общей оценки (49), демонстрирующим близость ее границ.

Схематично разберем случаи р Е (1, 2) и р Е (2, 3).

Случай р Е (1, 2). Здесь p = 1, и поэтому (см. (37)) работаем с представлением

I ₁ (a, 6) = ^ ln (a ² + 2a cos 6 + 1) — a cos 6, a >  0, 6 Е ( — п, п).

Согласно (23) имеем г 1 ⁺⁾ = [п/2,3п/4]. Записав (49) для текущего случая, получим

C (р) >

C (р) <

max sup θ ∈ ^π ₂ , ³ ₄ ^{π a>0}

¹ ₂ ln( a ² +2 a cos θ +1) - a cos θ

a P                  ^;

max 9 С [ 2 ,^п ]

sup a> 0

¹ ₂ ln( a ² +2 a cos θ +1) - a cos θ a ^ρ

Отдельные рутинные вычисления позволяют осуществить в (50) оптимальный выбор значений 6 = 3п/4 и 6 = п соответственно и одновременно сузить промежуток изменения параметра a > 0. В итоге, удается придать форме записи соотношений (50) более компактный вид:

2 Р/ 2 - 1 m^ $ - „+У+a ^ C(р) ^ m„^ln(a ^— -1>±a, , е ₍1,₂>.     (51)

Нетрудно убедиться в том, что двойное неравенство (51) усиливает прежний результат (46). Действительно, огрубляя оценку снизу в (51), при всех р Е (1, 2) имеем

C(р) > 2Р/2-1 max ---a ± 1) ± a > 2Р/2-1     ---a ± 1) ± a

= 2 ^{- p/2} a =2

a 2          ap                             ap что дает оценку снизу в (46). Далее, огрубляя оценку сверху в (51), при всех р Е (1, 2)

имеем

C (р) с max1П        = max■ G- "a 1-±^ < 2^ Л ± max     1 , a>2       ap          a^*2             a               у    a>2     a у что дает оценку сверху в (46). Если же для огрубления левой части (51) привлечь неравенство ln(x + 1) > x--2, x Е [0, +to), то простые подсчеты дадут возможность заменить нижнюю границу в (46) на б´ольшую элементарную миноранту:

C (р) >  2 ^{4 - 3p/2} (3 _— р) 4 - ^р > 2 ^{- p/2} ,    р Е (1, 2).

Наконец, неравенство ln(x + 1) < x, x G (-1, +ro), позволяет при тех же р G (1, 2) провести в правой части (51) выкладку

C (р) ^ _max            ' ^ _max ^o-l)

2(a - 1)           _ 2(р - 1) ^{p - 1}

a ^P     a=p/(p-1) ”       ^{p P}

a> 2        a ^p           a ^ 2     a ^p

Полученная оценка усиливает (47), поскольку для любого значения р G (1, 2) справедливо неравенство

2(р - 1) ^{р - 1}     2 2 ^{- р}

ρρ     < ρ , сводящееся к очевидному неравенству

(-у^{- 1} < 1, р G (1,2).

Коснемся вопроса о предельном поведении экстремальной функции C(р) в целых точках. Из «явной» формулы (45) можно получить (см. [8]) соотношения lim Cри    +х.,    lim C(р) _ 1.

ρ→0+

Как указано в [20], неравенства (46), (47) влекут наличие предела limnC(р) _ 1 • р >2 0

Не ясно, однако, существует ли lim _p , |.о C (р). Новое двойное неравенство (51) позволяет оценить границы возможной неопределенности величины C (р) при р ^ 1+0 и показывает, что если односторонний предел lim _p , _|+о C (р) существует, то он чуть больше единицы и не совпадает с lim _p ^ i _- o C (р) _ 1 (см. теорему 3 ниже).

Полученную информацию о функции C (р) при р G (1, 2) соберем в одно утверждение.

Теорема 3. Пусть C (р) — точная нижняя грань типов ^ p (f ) целых функций порядка р, все корни которых отрицательны и образуют последовательность Л _ A f верхней плотности А р (Л) _ 1 и нижней плотности А р (Л) _ 0 . Тогда при всех р G (1, 2) справедлива двусторонняя оценка

2 р/ 2 - 1 max '                a ^ с ^ max '     ' '

a^2          ap                      a>2       ap влекущая оценку через элементарные функции

2 4 - 3 P/ 2 ³         _p с _p²          ' , р G

(4 - р)4-Р                  рР     , p v i h а также соотношения lim C(р) ^ ^2 (1 + max ln 2 - a+1) ^ _ 1.0109 ... ;

. р ^ 1+0          ² V     a ^²            )

lim C(р) 2    a                 , первое из которых ввиду (54) показывает, что при р ^ 1 функция C(р) не имеет предела.

Далее изложение ведем совсем тезисно.

Случай р Е (2, 3). Здесь p = 2. Согласно (24), (37), (49) для указанных р получим

C (р) >

C (р) ^

max su 2 ln(a ² +2a cos 9 +1) — a cos 6 + a 2 cos 26

6g[o,6]u[3п,5П] a>0                  a max su 2 ln(a2 +2acos6+1)—acos6+ a2 cos26

6 G [ 0 , 6 ] u [ 3 П ,n ] ^a >0                  a

Отсюда, например, следует, что при всех значениях р Е (2, 3) верны цепочки неравенств

3 ^р/2

C(р) ^ --- max

^М ’     2 a ^ 2

ln (a— a + 1) + a + a"

^ 4 ₃ (4 - P ) / 2

aρ ln(a - 1) + a + —        2 ln(a - 1) + a + —

C (р) < max-------------— = max a p-------~-----— < a^ 2         ap            a^ 2               a2

(D2

а также оценки

lim C (р) ^ — max p , 2-0          ^{2 a} ^ ²

ln (a— a + 1) + a + a"

a ²

4,

f\       ln(a - 1) + a + T

= 1 ,

lim C (р) < max--------^------- p^2+0   ' ’    a^ 2          a2

указывающие (см. (55)) на отсутствие у функции C (р) предела при р ^ 2, и оценки

3V3 lim C (р) >---max

Р - 3 0              ^{2 a} ^ ²

ln (a— a + 1) + a + a"

a ³

= 0.5181... ,

---    , . ln(a — 1) + a + lim C(р) < max---------=--------= 0.5789 ...

^p ^ ^{3 —} 0          a^ 2          a⁶

Наконец, численная оценка C (р) > 0.51, р Е (2, 3), подкрепляет прежний результат (48).

На этом закончим разбор случаев, поскольку, как видно, дальнейшее увеличение значений ρ сопряжено с вычислительными сложностями. Анализ проведенных расчетов придает правдоподобность следующей гипотезе: для любого p ∈ N существуют одно сторонние пределы lim _p , _p 0 C (р), lim _p , _p . 0 C (р), причем lim _p , _p 0 C (р) < lim _p , _p . 0 C (р). Было бы интересно также (в свете нетривиальной оценки (48)) выявить точный закон асимптотического поведения C (р) при р ^ + то , р / N.

Полученные результаты о наименьшем типе хотя и улучшают предыдущие, но все же носят не вполне законченный характер ввиду определенного «зазора», имеющегося в опорной формуле (49). По-видимому, для любых p Е N и р Е (p, p+1) максимум в левой части (49) достигается при 6 = 2p+2 п, а в правой части — при 6 = п. Как бы то ни было, для устранения означенного зазора нужно дополнить теорему 2 точной информацией об индикаторе hp(f, 6) на отрезке 6 Е [2p+2 п, п], что позволит в явном виде, подобном (45), выписать экстремальную функцию C(р) ив полном объеме изучить ее свойства при всех нецелых значениях р > 0. После этого логичен переход к целым функциям с от- рицательными корнями ненулевой нижней плотности. Как представляется, реализация намеченных перспектив требует масштабного исследования, развивающего аналитические разработки А. Данжуа [21], А. Ю. Попова [20] и авторов [7].