Оценки решения балансовой модели, учитывающей экологический фактор и вложение инвестиций

DOI:

Актуальными задачами экономического развития общества на современном этапе остаются задачи эффективного прогнозирования, управления экономическими системами, планирования. Большинство современных моделей, имеющих практичес- кую направленность и предназначенных для прогноза основных показателей экономики, построены на расширенных моделях межотраслевого баланса. Макроэкономические модели описывают экономику как единое целое, связывая между собой укрупненные материальные и финансовые показатели: производство, потребление, инвестиции, за- нятость и др. [Karlin, 1995, p. 907–938; То-ропцев, 2001, с. 10–20].

Развитие экономики неизбежно влечет за собой загрязнение окружающего мира. Выделение вредных отходов в процессе производственной деятельности приводит к борьбе с загрязнением окружающей среды. Часть вредных отходов может подвергаться утилизации и переработке. С усилением требований на ограничение выбросов вредных отходов переработка отходов становится актуальной и, соответственно, это влечет увеличение вложений инвестиции в их переработку.

Изложенные выше факторы принимаются во внимание в модели, предложенной в статье. В силу того что в макроэкономической модели учитывается вложение инвестиций, описание модели представляет собой систему дифференциальных уравнений. Учет выделения вредных отходов и их переработка приводят к тому, что заданные параметры системы могут принимать отрицательные значения. Проблема поиска положительного решения модели сводится к нахождению положительного решения операторного уравнения с дифференциальным оператором при наличии заданных неотрицательных и отрицательных величин.

Точное решение динамической балансовой модели c нелинейной зависимостью представляет некоторые трудности, связанные как с достаточно большим количеством данных, так и с методами решения таких моделей. В ряде случаев при построении и исследовании модели на начальном этапе не требуется знание точного решения, а достаточно иметь некоторую его оценку, позволяющую судить об адекватности модели. В связи с этим представляют интерес легко реализуемые методы получения оценок решения модели с непрерывным временем.

Методология проведения работы

Исходя из жизненного опыта и особенностей технологических процессов, значительно удобнее рассматривать модель не с дискретным временем, а считать, что время непрерывно. Макроэкономическая модель, в которой учитываются выделения вредных от- ходов и вложение инвестиций, описывается системой уравнений:

,. _ . ,.     . , _х _ dx ( t ) „ dy ( t )        ,

х(t) - А11 х(t) + A12y(t) + Bl1      + B12 , + fl (tX dt dt

,. _ . ,.     .    , _x _ dx ( t ) „ dy ( t )

• ■ y ⁽ t ) >  A 21 x ⁽ t ) + A 22 y ⁽ t ) + B 21       + B 22 —-- f , ⁽ t XQl)

dt dt

x(t) > 0, y (t) > 0. _ где х(t) – вектор валового выпуска полезного продукта; y(t) – вектор вредных отходов в окружающей среде, возникающих в процессе производства и подлежащих уничтожению; f1(t) – вектор чистого выпуска полезного продукта; f2(t) – вектор остаточного уровня вредных отходов ; A11 - (n х n) технологическая матрица; Al2 - такая (n х m) матрица, что Al2y(t)- вектор полезного продукта, возникающий при переработке вредных отходов в объеме вектора y; A2l такая (m х n) матрица, что A2l x(t) - вектор вредных отходов, создаваемых при выпуске полезного продукта в объеме вектора x; A22 – такая (m х m) матрица, что при уничтожении вектораy вредных отходов в окружающую среду выделяется вредных отходов в объеме вектора A22y(t); B 11 - матрица, характеризующая инвестиции части созданного в момент времени t i-го продукта на создание дополнительного резерва производства для выпуска продукции; B12 – матрица инвестиций, идущих на подавление вредных отходов, возникающих при создании дополнительного резерва производства; B21 – матрица, характеризующая количество выделяемых единиц вредных отходов при увеличении производства полезного продукта; B22 – матрица, характеризующая количество выделяемых вредных отходов, при подавлении вредных отходов, выделяющихся при увеличении годового производства продукта x.

Пусть промежуток времени [ 0; T ] - период прогноза.

Множество неотрицательных функций { х ( t ), y ( t )} , t e [ 0; T ] , удовлетворяющих системе неравенств (1.1), будем называть множеством планов модели (1.1) и обозначим это множество функций через П .

Если множество планов задачи (1.1) не пустое, то оно, как правило, содержит бесконечное множество элементов.

Решение { х ( t ), y ( t )} из П , удовлетворяющее условию

{х •(t), y *(t )}= {inf {x(t)}, inf {y(t)}}, будем называть решением динамической балансовой модели [Исследование операций в экономике ... , 1997, с. 16–20].

Представим модель (1.1) в операторном виде. Обозначим:

/ X /          х / X        ' dx ⁽ t ⁾

f .(   (t) 1 A = A11  A21) - = x (t) 1 dz = dt l-f2( t) J     IA12   A22 J     l y(t) J dt    dy( t)

I dt J

B ll    B 21 1

B 12   B 22 J

1. В этом случае, система (1.1) перепишется следующим образом [Павлова, 2005, c. 30–35]

Z = AZ + B — + f . dt

(1.2)

Выразим из операторного уравнения z .

Если существует обратная матрица (E - A)-1, то z = (E - A)-1. Bd- + (E - A)-1 f.

dt

Последняя система уравнений эквивалентна операторному уравнению dz z = C+ g dt ,

( C 11    C ₁₂

C = (E - A)-1 B, g = (E - A)-1 f, C = 1 r l C 21 C 22

,

где

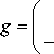
g 1 ⁽ t⁾ ) g 2 ⁽ t ⁾ J .

Следовательно, модель (1.1) примет вид [Павлова и др., 2012, с. 46]:

x ⁽ t⁾ = d ^С 11 x ⁽ t^{) +} d ^С 12 У ⁽ t^{) +} g 1 ⁽ t⁾, dt         dt

(1.3)

Замечание. Оператор вида

C i^J ( ^ф ) = "dt^{C i} ^ (tt ) в рассматриваемом нами случае означает, что производная по t берется от произведения матрицы на вектор, координаты которого являются функциями от t . В дальнейшем нам понадобится монотонность операторов C ij по ф(t ), для этого необходимо потребовать выполнение условий, позволяющих дифференцировать неравенства. Например, для монотонности операторов C_ij достаточно, чтобы функции x ( t ) и y ( t ) были непрерывными и неубывающими (в этом случае операторы будут линейными положительными, а значит, и монотонными).

Предположение о том, что функции x ( t ) и y ( t ) неубывающие, является естественным и с экономической точки зрения: с течением времени в стабильном и развивающемся обществе валовой выпуск продукции и выброс вредных отходов в окружающую среду при данной технологии и имеющемся перечне товаров не уменьшается.

Перепишем модель (1.4) в виде z = C (z) + g, (1.5)

где С – положительный оператор сo спектральным радиусом меньше единицы. При этом для (1.5) работает итерационный метод [Стеценко и др., 2004, с. 51–53], который в общем виде представим:

• ^- „ +1 = C ^{( -} „ ) + g .

Построим оценки к решению этого уравнения. Итерационный процесс, предложенный в [Павлова и др., 2012, с. 73–74], строится следующим образом. Выбираются начальные приближения Uo и v0, удовлетворяющие соотношениям u0 ^ Vo, u0 < C(u0) + g, C(V0) + g < V0

(запись u < v означает, что компоненты вектора v - и неотрицательны).

Последовательные приближения u k , v_k и ~_к , ~ _k находятся по следующим формулам:

~0 = и0, ~0 = v0, uk=1 = C (~k)+g, vk=1 = C (~к)+g

~k +1 =;-------- ^{( u} k +1 ⁺ Pk +1 ^V k +1 X

^{1 +} Pk +1

~ k +1 =     —^{( V} k +1 ⁺ q k +1 ^u k +1 ⁾

^{1 +} q k +1

(1.6)

k = 1,2,...

Здесь неотрицательные параметры pk=1, qk=1 выбираются так, чтобы на каждом шаге были выполнены соотношения uk < uk+1, vk+1 < V.

Как показано в [Исследование операций в экономике, 1997, c. 407], получаемые последовательные приближения сходятся к решению z^* задачи (1.5). При этом процесс (1.6) монотонен:

C ( u k ) ⁺ g < ~ k < z * < ~ k <  C ( v k ) ⁺ g .

Если в итерационном процессе (1.6) параметры pk, qk определены соотношениями pk = max{ p: p > 0, ~k - ~k-1 > p (~k-1- ~k)} qk = max{ q: q > 0, ~k-1- ~k > q (~k- ~k-1)}

~k+1 = C (Uk ) ~k+1 = C V)        , тогда справедлива оценка

Здесь A ₁ ⁽2⁾ - такая ( n x m ) матрица, что:

• -    A 1⁽2) y ( t ) - вектор полезного продукта, возникающий при переработке вредных отходов в объеме вектора y ;

• —    A 12 y ( t ) - вектор полезных продуктов, затрачиваемых на переработку вектора y вредных отходов (утилизация отходов);

• -    B 1⁽2) y ( t ) - матрица инвестиций, идущих на подавление вредных отходов, возникающих при создании дополнительного резерва производства;

• —    Bn у ( t ) — вектор инвестиций, высвобождаемых за счет утилизации вредных отходов.

Представим модель (2.1) в операторном виде. Обозначим:

A = [ A 11   A n ^-f⁰ A !? ) _f = f f 1 ⁽ t ) )

l A 21    A 22 j 1^{0   0} j I- ^f 2 ⁽ t )7

f x ( t )) dz z = I Z^l, l y ( t ) j dt

f ^{dx (} t ))         ,             .     .           .

.dt,  B = f B n B ^l-f⁰ B² 1

dy(tl,     lB21 B22 J 10   0 J l dt j

I ~ k +1

-

~ k +1|| <

x - 1 x +1

ql vk

-

^u k ,

В этом случае система (2.1) будет представлена операторным уравнением (1.2):

1nf( c : x >  cy ) _/ 2

где ;    7 ; < x . Число x назовем постоян- sup( c: cx < y)              Л ной фокусирования.

Решение модели можно получить, используя метод последовательных приближений. При этом метод сходится со скоростью убывающей геометрической прогрессии.

Рассмотренная выше модель получила дальнейшее развитие [Павлова и др., 2016, с. 70–72]. Модель, которая учитывает не только выделенные отходы, но и их переработку, с учетом вложенных инвестиций, представим следующим образом:

X ( t ) = А 11 х ( t ) + ( An - An) ) У ( t ) + B 11 dxt) +

( B  - C ) dy(l + f, ( t ),

У ⁽ t ) = A 21 x ⁽ t ) ⁺ A 22 У ⁽ t ) ⁺ B 21 dx ( t ) ⁺ dt

(2.1)

dy ( t )

^{B 22} dt

-

f 2 ( t ),

x(t) > 0,y(t) > 0,d^ > 0,dyt) > 0,t e [0;T]. dt dt z = Az + B--+ f dt .

Аналогично преобразованиям модели

• (1.1)    модель (2.1) примет вид

^{x (} t ) = d С"^{x (} t ) ⁺ d С 1⁽2⁾ у ⁽ t ) ^- d С 122) у ⁽ t ) ⁺ g 1 ⁽ t ), dt         dt          dt

У ⁽ t ) = d С 21 x ⁽ t ) ⁺ d С 22 У ⁽ t ) ^- g 2 ⁽ t )

I dt           dt или

■ x = С11( x) + С1(2)( y) - С<2’( y) + g 1, y = С21 (x) + С22( y) - g 2, где Cij (x), Cij (y) i,j = 1,2 – монотонные операторы.

Если операторы C_ij удовлетворяют условиям Липшица:

IICXu) -Ci(v)|| < qL> - V(1 = 1,2), где qLi – константа Липшица, а также существуют элементы u1,ν1, u2,ν2, удовлетворяющие условиям:

0 <  U 1 <  U ₂, 0 <  V , <  V ₂

' u 1 <  C _n( u 1 )+ c <2> ( V 1 ) - C24 v 2 )+ g 1 ,

^u 2 >  C _n( u 2 ) + C <2) ( v 2 ) - C <²⁾ ( V 1 ) + g 1 ,

V1 < C 21 ( u 1) + C 22 (v1) - g 2,       , v2 > C21 (u2) + C22(v2) - g2.

то существует единственное решение модели (2.1) [Стеценко и др., 1998, с. 74–75], причем u 1 < x*< u2, v < y*< V2.

Результаты работы

В общей постановке модель (2.1) можно переписать в виде операторного уравнения с монотонно разложимым оператором:

• 2.    С ( z ) = C ₁( z ) – C ₂( z ) [Островский, 1977, с. 233–238; Кубекова и др., 2001, с. 846–854]:

z = C ₁( z ) – C ₂( z ) + g .        (2.2)

Здесь C1(z), C2(z) – монотонные операторы. Операторное уравнение (2.2) целесообразно записать в виде z = (C1 – C2) (z) + g,           (2.3)

где z =

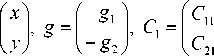
I 0    C 12    I

(0    0 J"

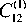
c

C =

По уравнению (2.3) построим новое уравнение

- ■—’ где z =

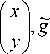
~ = C (~)+ g ,

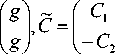
C 2

C 1

Элемент ^~ z можно рассматривать как элемент нового пространства E = ( e , E ) с нормой || ~ 11 = I | x || +1 | y | I , полуупорядоченного конусом K = ( K ,- K ) . При этом конус K «наследует» основные свойства конуса К.

Оператор C ₁ является монотонным (то есть из х 1 < х ₂ следует, что C ( x 1 ) <  C ( x ₂)), а C ₂ -антитонным (то есть из х 1 < х 2 => C ( x 1 ) >  С ( x ₂)) [Павлова, 2012, c. 100].

Пусть оператор C ^~(^~ z ) уравнения (2.4) монотонен, непрерывен и вполне непрерывен и удовлетворяет условиям Липшица

|| ^СЛ u ) ^{- C}i ( ^v )|| <  qLi ||u ^{- v}| ( i = i,² )

и пусть u_{k+ 1}= C ₁( u_k ) – C ₂( v_k ) + g , v_{k+ 1}= C ₁( v_k ) – C ₂( u_k ) + g, причем u ₀, v ₀ удовлетворяют неравенствам

^C 1 ⁽ u 0 ) ^{- C} 2 ^{( V} 0 ) ⁺ g >  u 0 , ^C 1 ^{( V} 0 ) ^{- C} 2 ⁽ u 0 ) ⁺ g <  ^V 0

и положим

*

u k +1

^u k +1 ⁺ m k ^v k +1 v •   = ^v k +1 + m k u k +1

1 + m k    ’ k ^{+ 1}        1 + m_k

^{- v} k + 1 ) ,] u k ) "

где m k = max-

m : uk + 1 ^- uk >  m ( ^v k ^v k ^{- v} k + 1 >  m ⁽ u k + 1 ^-

Тогда имеют место неравенства

**   *   **

u ₀<  u 1 <  u k < ... <  z < ... <  v k <  v 1 <  v ₀ (2.5)

и либо метод сходится за конечное число шагов, либо верна оценка:

|| v k +1 - u k +1|| <  Х+д qM ^{- u} >\ V q _L – константа Липшица.

Область применения результатов

Построение отрезка (2.5) можно рассматривать как один шаг рекуррентного процесса по уточнению двусторонних границ неизвестного решения х^* исходного уравнения. Повторяя этот процесс достаточное число раз, мы в итоге получим метод построения двусторонних приближений, который можно рассматривать как метод ускорения сходимости двусторонних приближений u_n,ν_n в случае уравнения с монотонно разложимым оператором.

Рассмотрим еще один метод двусторонних приближений, позволяющий оценить решение моделей.

И динамическую модель, учитывающую подавление вредных отходов, и модель, учитывающую переработку, можно представить в виде операторного уравнения (2.4).

При этом будем предполагать, что спектральный радиус оператора С меньше единицы.

При сделанных предположениях к решению уравнения будут сходиться последовательные приближения и для одной и для другой моделей:

z + . 1 = C (~) + ~, ( i = 0,1,2,... ) .

Предположим, что найдено несколько первых элементов последовательности. Ставится вопрос: как, не прибегая к новым итерациям, а используя лишь найденные приближения, получить более точные приближения к решению z* [Исследование операций в экономике, 1997, c. 407]. При этом для нас особый интерес будут представлять приближения к z* «по недостатку» и «по избытку». Если для последовательных приближений zk-p, zk, zk+p, где k и p - фиксированные натуральные числа (k > p), выполняется неравенство zk+p — zk < /(zk — zk—p), причем 0< у <1.

Тогда для решения z* уравнения рассматриваемого уравнения справедлива оценка

^z * <  z k + p ^{+       (} z k + p ^— z k )

^{1 —} Y

Если для последовательных приближений z_k - _p , z_k , z_{k + p} , где k и p - фиксированные натуральные числа ( k >  p ), выполняется неравенство

e(zk - zk-p) < zk+p- zk, где в e (0; 1).

Тогда для решения z* уравнения справедлива оценка ных приближений. Двусторонние оценки и описанный метод ускорения приближений к решению убеждают в адекватности рассматриваемой модели, не прибегая к нахождению точного решения.